归并排序法01:实现归并排序法
归并排序法是一种高级排序算法
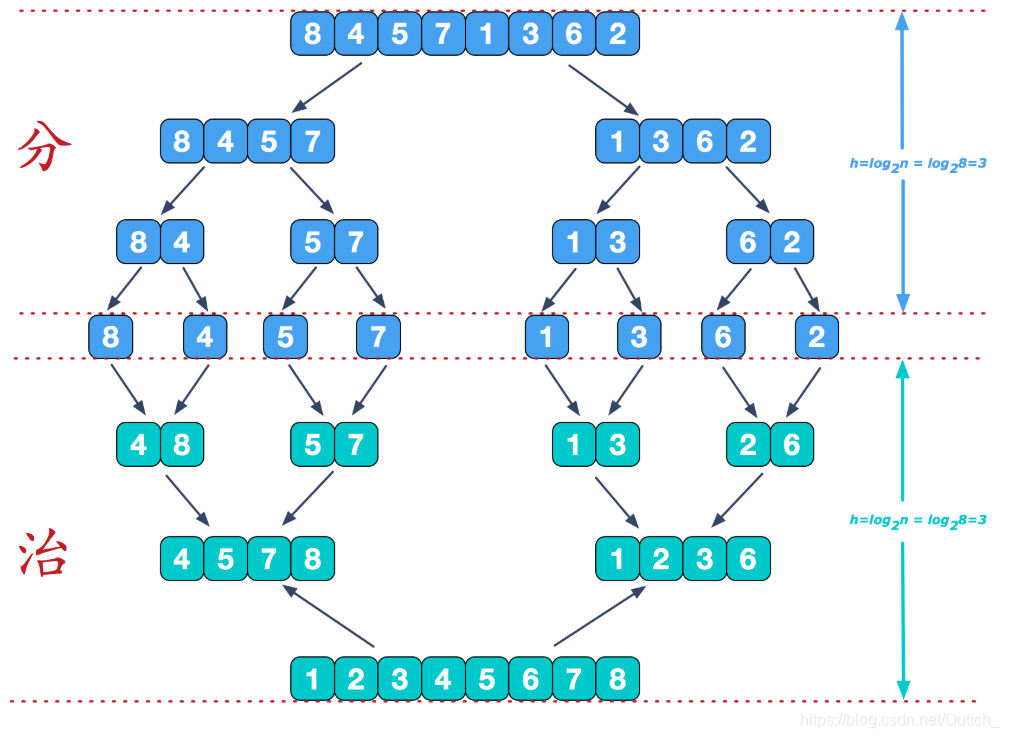
核心思想:归并排序法是一种分治算法,将一个数组递归的一分为二,二分为四...定义一个merge()方法对两个子数组分别进行遍历比较,选出较小的元素放在前面,最终完成排序
递归实现归并排序法
import java.util.Arrays;
public class Algorithm {
public static void main(String[] args) {
Integer[] arr = {6,6,3,2,4,7};
MergeSort.sort(arr);
System.out.println(Arrays.toString(arr));
}
}
class MergeSort {
private MergeSort(){}
/**
* 用户只需要传入一个数组即可
*/
public static<E extends Comparable<E>> void sort(E[] arr){
sort(arr, 0, arr.length - 1);
}
/**
* 为了实现递归,必须要有拆分数组的边界索引,因此定义一个私有、对用户不可见的方法来进行递归
*/
private static<E extends Comparable<E>> void sort(E[] arr, int left, int right){
/**
* 如果元素个数小于等于1,不需要进行操作
*/
if (left >= right){
return;
}
/**
* left + right有可能会产生整型溢出,因此写成如下方式可以避免出现这种错误
*/
int mid = left + (right - left) / 2;
/**
* 递归的拆分区间
*/
sort(arr, left, mid);
sort(arr, mid + 1, right);
/**
* 对有序的两个子区间进行最终的排序
*/
merge(arr, left, mid, right);
}
/**
* 有序子区间arr[left, mid]和arr[mid + 1, right]
*/
public static<E extends Comparable<E>> void merge(E[] arr, int left, int mid, int right) {
/**
* left和mid + 1是两个子数组的开始索引,表示当前进行比较的元素索引
*/
int i = left;
int j = mid + 1;
/**
* 因为对arr数组原地排序,数组元素会动态发生变化,不能正常读取下一个元素。因此先保存一下两个有序的子区间副本,根据副本的顺序来读取元素
* 副本只需要保存当前的子区间[left, right + 1]而不是整个arr数组,否则空间复杂度会很大
* Arrays.copyOfRange()方法按指定范围拷贝数组,注意结束索引是不包含的
*/
E[] tem = Arrays.copyOfRange(arr, left, right + 1);
for (int n = left; n < right + 1; n++) {
/**
* 如果i和j走到了自己小区间的边界,说明这个子区间已经排好序了,剩下的就是将另一个子区间的元素直接添加进来
* 因为tem数组的索引是从0开始的,而我们要操作的arr数组是从left开始的,tem[0] == arr[left],i和j是由arr数组赋值的,所以跟tem有一个left的偏差
*/
if (i == mid + 1){
arr[n] = tem[j - left];
j++;
}
else if (j == right + 1) {
arr[n] = tem[i - left];
i++;
}
else if (tem[i - left].compareTo(tem[j - left]) <= 0) {
arr[n] = tem[i - left];
i++;
}
else{
arr[n] = tem[j - left];
j++;
}
}
}
}
拓展:利用辅助方法,打印递归的分步信息
import java.util.Arrays;
public class Algorithm {
public static void main(String[] args) {
Integer[] arr = {6,6,3,5,4,7,4,5,6,7,9};
MergeSort.sort(arr, 0);
System.out.println(Arrays.toString(arr));
}
}
class MergeSort {
private MergeSort(){}
public static<E extends Comparable<E>> void sort(E[] arr, int depth){
sort(arr, 0, arr.length - 1, depth);
}
private static<E extends Comparable<E>> void sort(E[] arr, int left, int right, int depth){
String depthScale = depth(depth);
System.out.print(depthScale);
System.out.println(String.format("当前要排序的数组是arr[%d, %d]", left, right));
if (left >= right){
return;
}
int mid = left + (right - left) / 2;
sort(arr, left, mid, depth++);
sort(arr, mid + 1, right, depth++);
System.out.print(depthScale);
System.out.println(String.format("当前排序完成的数组是arr[%d, %d]和arr[%d, %d]", left, mid, mid + 1, right));
merge(arr, left, mid, right, depth++);
System.out.print(depthScale);
System.out.println(String.format("当前合并完成的数组是arr[%d, %d]", left, right));
}
public static<E extends Comparable<E>> void merge(E[] arr, int left, int mid, int right, int depth) {
int i = left;
int j = mid + 1;
E[] tem = Arrays.copyOfRange(arr, left, right + 1);
for (int n = left; n < right + 1; n++) {
if (i == mid + 1){
arr[n] = tem[j - left];
j++;
}
else if (j == right + 1) {
arr[n] = tem[i - left];
i++;
}
else if (tem[i - left].compareTo(tem[j - left]) <= 0) {
arr[n] = tem[i - left];
i++;
}
else{
arr[n] = tem[j - left];
j++;
}
}
}
/**
* 打印分隔符,递归深度越深,分隔符越长
*/
public static String depth(int depth){
StringBuilder str = new StringBuilder();
for (int i = 0; i < depth; i++) {
str.append("----");
}
return str.toString();
}
}
复杂度分析
从归并排序的递归树来看,递归深度为log2n,而每层所要处理的元素都是n个
因此归并排序的时间复杂度为O(nlogn)
选择、插入、归并排序法性能比较
import java.util.Arrays;
import java.util.Random;
public class Algorithm {
public static void main(String[] args) {
Integer[] testScale = {10000, 100000};
for (Integer n : testScale) {
Integer[] randomArr = ArrayGenerator.generatorRandomArray(n, n);
Integer[] sortedArr = ArrayGenerator.generatorSortedArray(n);
Integer[] arr1 = Arrays.copyOf(randomArr, randomArr.length);
Integer[] arr2 = Arrays.copyOf(randomArr, randomArr.length);
Integer[] arr3 = Arrays.copyOf(sortedArr, sortedArr.length);
Integer[] arr4 = Arrays.copyOf(sortedArr, sortedArr.length);
System.out.println("测试随机数组排序性能");
System.out.println();
Verify.testTime("SelectionSort", randomArr);
Verify.testTime("InsertionSort", arr1);
Verify.testTime("MergeSort", arr2);
System.out.println();
System.out.println("测试有序数组排序性能");
System.out.println();
Verify.testTime("SelectionSort", sortedArr);
Verify.testTime("InsertionSort", arr3);
Verify.testTime("MergeSort", arr4);
System.out.println();
}
}
}
class MergeSort {
private MergeSort(){}
public static<E extends Comparable<E>> void sort(E[] arr){
sort(arr, 0, arr.length - 1);
}
private static<E extends Comparable<E>> void sort(E[] arr, int left, int right){
if (left >= right){
return;
}
int mid = left + (right - left) / 2;
sort(arr, left, mid);
sort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
public static<E extends Comparable<E>> void merge(E[] arr, int left, int mid, int right) {
int i = left;
int j = mid + 1;
E[] tem = Arrays.copyOfRange(arr, left, right + 1);
for (int n = left; n < right + 1; n++) {
if (i == mid + 1){
arr[n] = tem[j - left];
j++;
}
else if (j == right + 1) {
arr[n] = tem[i - left];
i++;
}
else if (tem[i - left].compareTo(tem[j - left]) <= 0) {
arr[n] = tem[i - left];
i++;
}
else{
arr[n] = tem[j - left];
j++;
}
}
}
}
class InsertionSort {
private InsertionSort() {}
public static <E extends Comparable> void sort(E[] arr) {
for (int i = 1; i < arr.length; i++) {
E tem = arr[i];
int j;
for (j = i; j > 0 && tem.compareTo(arr[j - 1]) < 0; j--) {
arr[j] = arr[j - 1];
}
arr[j] = tem;
}
}
}
class SelectionSort {
private SelectionSort(){}
public static<E extends Comparable<E>> void sort(E[] arr){
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j].compareTo(arr[minIndex]) < 0) {
minIndex = j;
}
}
if (i != minIndex) {
E tem;
tem = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = tem;
}
}
}
}
class ArrayGenerator {
private ArrayGenerator (){}
public static Integer[] generatorRandomArray (Integer n, Integer maxBound){
Integer[] arr = new Integer[n];
Random random = new Random();
for (int i = 0; i < n; i++) {
arr[i] = random.nextInt(maxBound);
}
return arr;
}
public static Integer[] generatorSortedArray (Integer n){
Integer[] arr = new Integer[n];
for (int i = 0; i < n; i++) {
arr[i] = i;
}
return arr;
}
}
class Verify {
private Verify (){}
public static<E extends Comparable<E>> boolean isSorted(E[] arr){
for (int i = 0; i < arr.length - 1; i++) {
if (arr[i].compareTo(arr[i + 1]) > 0) {
return false;
}
}
return true;
}
public static<E extends Comparable<E>> void testTime(String AlgorithmName, E[] arr) {
long startTime = System.nanoTime();
if (AlgorithmName.equals("SelectionSort")){
SelectionSort.sort(arr);
}
if (AlgorithmName.equals("InsertionSort")) {
InsertionSort.sort(arr);
}
if (AlgorithmName.equals("MergeSort")) {
MergeSort.sort(arr);
}
long endTime = System.nanoTime();
if (!Verify.isSorted(arr)){
throw new RuntimeException(AlgorithmName + "算法排序失败!");
}
System.out.println(String.format("%s算法,测试用例为%d,执行时间:%f秒", AlgorithmName, arr.length, (endTime - startTime) / 1000000000.0));
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号