[Problem 16]欧拉

2¹⁵ = 32768 and the sum of its digits is 3 + 2 + 7 + 6 + 8 = 26.

What is the sum of the digits of the number 2¹⁰⁰⁰?

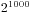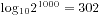这一题必须要使用“高精度乘法运算”进行计算（的位数是）。学到的：

1. 高精度运算（百度百科：高精度运算，是指参与运算的数(加数,减数,因子……）范围大大超出了标准数据类型（整型，实型）能表示的范围的运算。例如，求两个200位的数的和。这时，就要用到高精度算法了）。针对的情况就是要运算的数值远远超出了计算机语言提供的数据类型所能表达的范围。这种情况下，无论是加减乘除法运算，都需要用一个数组来表示这个大数。具体加减乘除运算，只要返璞归真，考虑“笔算”时候的算法，进行逐位运算就对了。
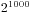1.1的位数是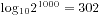
2. stack overflow。stack默认大小是1M。那么，在考虑用数组表示大数的情况下，这个数组就会变得非常大。比如int a[300]表示一个300位的正整数。
3. 复习int* p = new int[100] & delete [] p;
--delete []的必要性：对于简单数据类型，[]可有可无；对于类，[]是必须的，因为需要调用析构函数（验证之）。
4. <cstring>下的memset是直接以byte为单位进行内存赋值的，因此对于char以外的数据类型慎用。

#include <cmath>
#include <iostream>
#include <cstring>
using namespace std;
#define N 304

int _tmain(int argc, _TCHAR* argv[])
{    
    int i = 0;
    char *a = new char[N];
    while(i < N)
    {
        a[i] = -1;
        i++;
    }

    a[N-1] = 8;    
    int iCnt = 3;
    int iUpN = 0;
    i = 0;
    while(iCnt < 1000) // 2^1000
    {
        iUpN = 0;
        i = 0;
        int product = 1;
        for(i = N-1; i >= 0; i--)
        {
            if(a[i] == -1)
                break;
            product = a[i] * 2;
            if(iUpN != 0)
                product += iUpN;
            a[i] = product % 10;
            iUpN = product / 10;
        }

        if(i == 0)
        {
            cout << "array  is not large enough!" << endl;
            break;
        }


        if(iUpN != 0)
            a[i] = iUpN;
         
        iCnt++;
    }

    int sum = 0;
    for(i = N-1; i >= 0; i--)
    {
        if(a[i] == -1)
            break;
        sum += a[i];
    }
    delete [] a;

    cout << "sum: " << sum << endl;
    
    
    return 0;
}