【数据结构】建立二叉树以及哈夫曼树及哈夫曼编码

文章目录

5.4.1 方式

5.4.2 由先根和中根遍历序列建二叉树

5.4.3 由后根和中根遍历序列建二叉树

5.4.4 由标明空子树的先根遍历建立二叉树

5.4.5 由完全二叉树的顺序存储结构建立二叉链式存储结构

5.5 哈夫曼树及哈夫曼编码

5.5.1 基本概念

5.5.2 最优二叉树

5.5.3 构建哈夫曼树

5.5.4 哈夫曼编码

5.5.5 哈夫曼编码类

5.4.1 方式

• 四种方式可以建立二叉树

  1. 由先根和中根遍历序列建二叉树

  2. 由后根和中根遍历序列建二叉树

  3. 由标明空子树的先根遍历建立二叉树

  4. 由完全二叉树的顺序存储结构建立二叉链式存储结构

5.4.2 由先根和中根遍历序列建二叉树

1）先根和中根原理

 

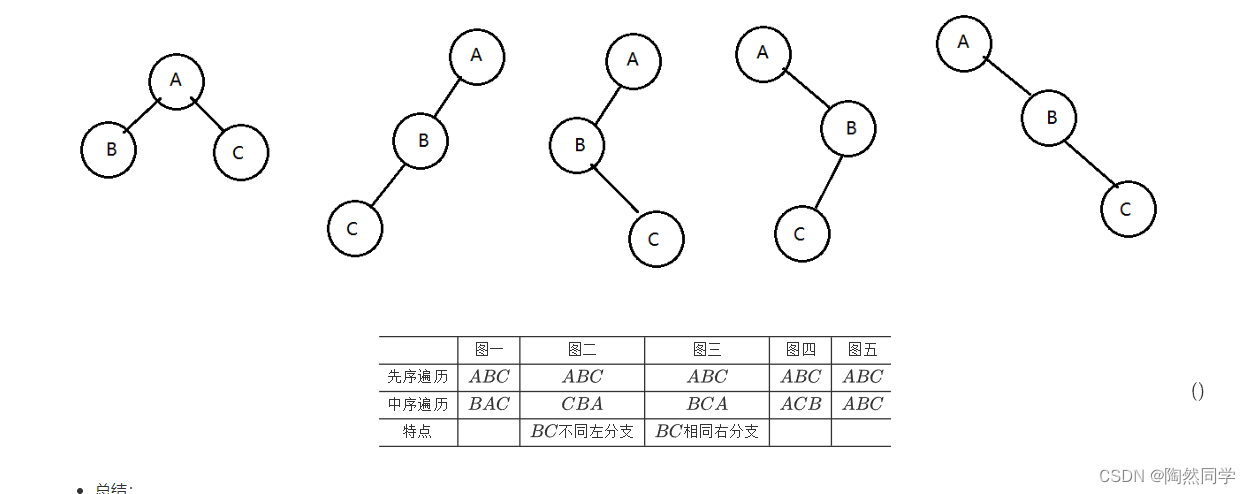
$$
\begin{array}{c|c|c} \hline &图一&图二&图三&图四&图五\\ \hline 先序遍历&ABC&ABC&ABC&ABC&ABC\\ \hline 中序遍历&BAC&CBA&BCA&ACB&ABC\\ \hline 特点&&BC不同左分支&BC相同右分支\\ \hline \end{array} \tag{}
$$

• 总结：

  • 通过先序遍历获得根结点（第一个结点）。

  • 通过根结点在中序遍历确定左子树和右子树。

2）实例分析

 

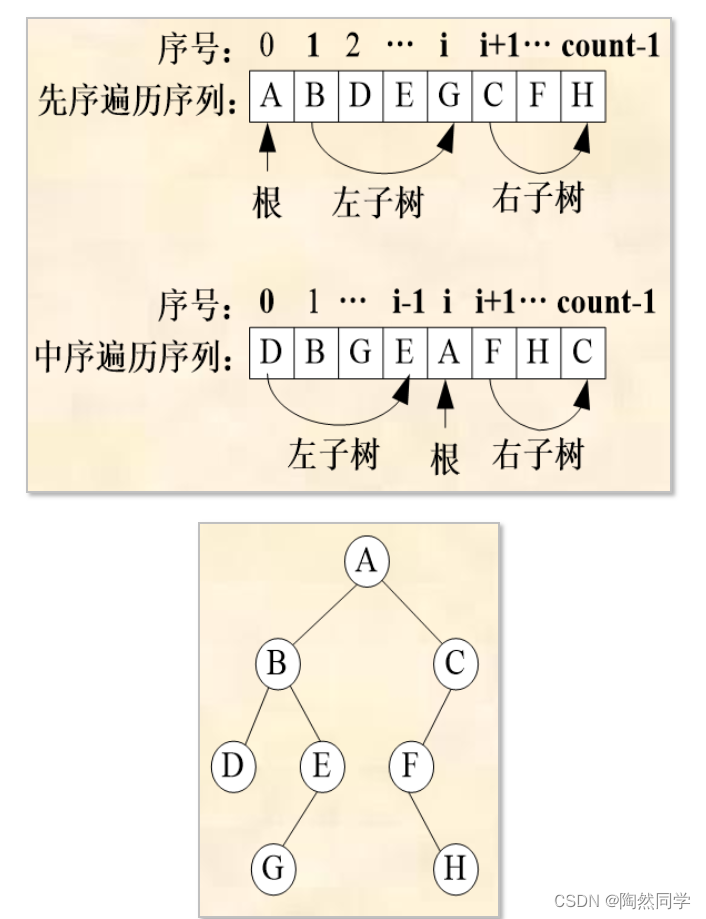
3）练习

• 练习1：

  已经二叉树，先序序列为abcdefg，中序序列为cbdaegf，重建二叉树？

  

   

• 练习2：

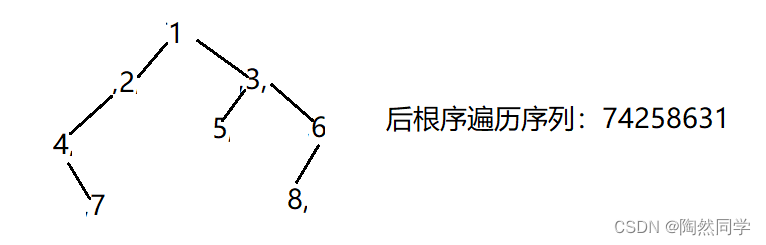
  已经二叉树，前序遍历序列为{1,2,4,7,3,5,6,8}，中序遍历序列{4,7,2,1,5,3,8,6}，后序遍历序列是？

  

   

• 练习3：

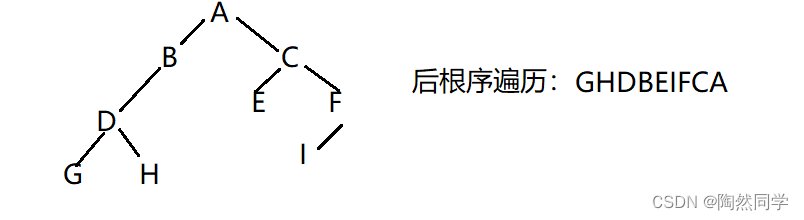
  已知一棵树二叉树的先根遍历和中根遍历的序列分别为：A B D G H C E F I和G D H B A E C I F，请画出此二叉树，并写出它的后根遍的序列？

  

   

4）算法

/** 例如：new BiTree("ABDEGCFH","DBGEAFHC",0,0,8);
* @param preOrder 先序遍历序列
* @param inOrder  中序遍历序列
* @param preIndex 在preOrder中开始位置
* @param inIndex  在inOrder中开始位置
* @param count 结点数
*/
public BiTree(String preOrder,String inOrder,int preIndex,int inIndex,int count) {
    if(count > 0) {
        //1 通过先序获得根结点
        char r = preOrder.charAt(preIndex);
        //2 中序中，根结点的位置
        int i = 0 ;
        for(; i < count ; i ++) {
            if(r == inOrder.charAt(i + inIndex)) {
                break;
            }
        }
        //3 通过中序，截取左子树和右子树
        root = new BiTreeNode(r);
        root.lchild = new BiTree(preOrder,inOrder,preIndex+1, inIndex, i).root;
        root.rchild = new BiTree(preOrder,inOrder,preIndex+1+i,inIndex + i + 1, count-i-1).root;
    }
}

5.4.3 由后根和中根遍历序列建二叉树

1）后根和中根原理

 

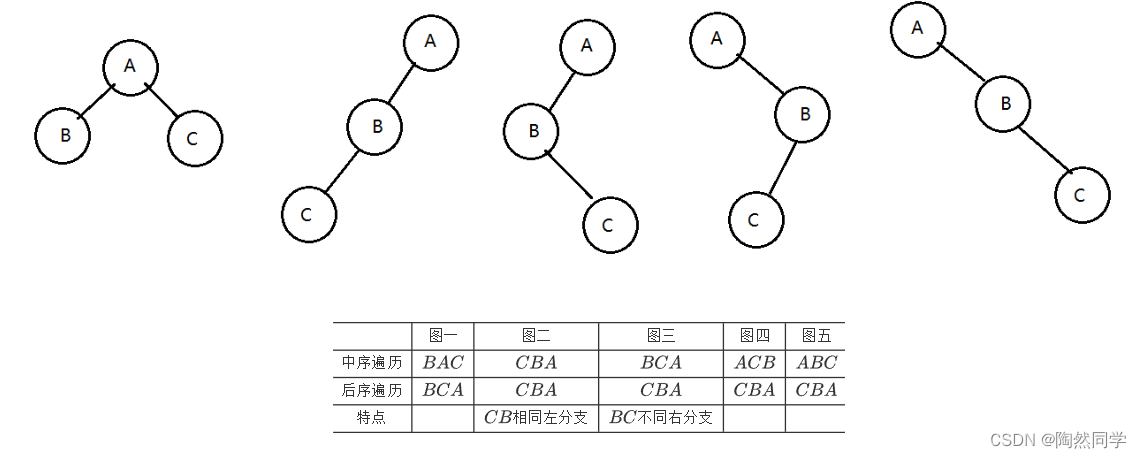
$$
\begin{array}{c|c|c} \hline &图一&图二&图三&图四&图五\\ \hline 中序遍历&BAC&CBA&BCA&ACB&ABC\\ \hline 后序遍历&BCA&CBA&CBA&CBA&CBA\\ \hline 特点&&CB相同左分支&BC不同右分支\\ \hline \end{array} \tag{}
$$

总结：

• 通过后序遍历获得根结点（最后一个结点）。

• 通过根结点在中序遍历确定左子树和右子树。

2）练习

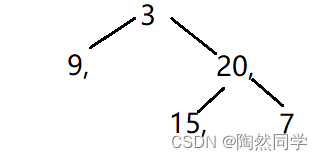
• 练习1：

  已知二叉树，中根遍历序列为：9,3,15,20,7、后根遍历序列为：9,15,7,20,3，重建二叉树？
  ​

 

• 练习2：

  已知二叉树，中根遍历序列为：6,3,4,1,5,8,2,7、后根遍历序列为：3,6,1,8,5,7,2,4，前根遍历序列？
  ​
  ​

 

• 练习3：

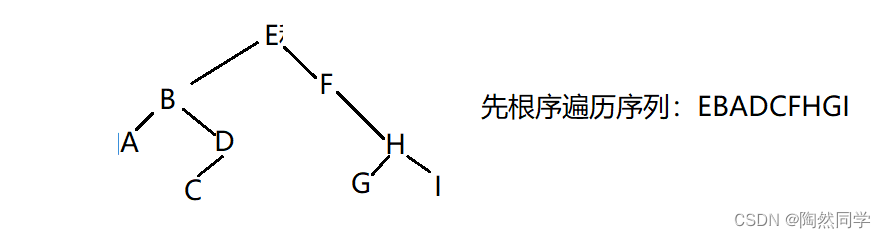
  已知一棵树二叉树的后根遍历和中根遍历的序列分别为：A C D B G I H F E和A B C D E F G H I，请画出该二叉树，并写出它的先根遍历的序列
  ​

  

   

5.4.4 由标明空子树的先根遍历建立二叉树

1）概述

• 仅使用先根遍历序列无法唯一确定一颗二叉树，例如：“AB”，B可以是左孩子，也可以是右孩子。

• 在先根遍历序列中加入==空树==信息，从而确定结点与双亲、孩子与兄弟间的关系，从而唯一确定一颗二叉树。

  • 空树：以字符“#”表示

  • 根节点A：以字符串“A##”表示

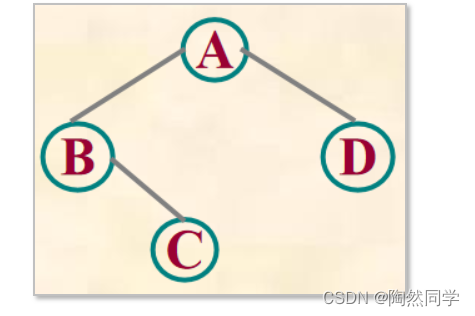
  • 下图树，以字符串“AB#C##D##”表示

    

     

2）算法

• 建立二叉链表算法分析：

  • 若读取的字符是“#”，则建立空树；否则

  1. 建立根节点

  2. 递归建立左子树的二叉链表

  3. 递归建立右子树的二叉

• 算法

  private int index = 0;          //用于记录preStr的索引值
  public BiTree(String preStr) {
      char c = preStr.charAt(index++);
      if(c != '#') {
          root = new BiTreeNode(c);
          root.lchild = new BiTree(preStr).root;
          root.rchild = new BiTree(preStr).root;
      } else {
          root = null;
      }
  }

5.4.5 由完全二叉树的顺序存储结构建立二叉链式存储结构

• 由二叉树的特性5可知，结点编号规则：

  • 根节点的编号为0

  • 编号我i的结点

    • 左孩子的编号为2i+1

    • 右孩子的编号为2i+2

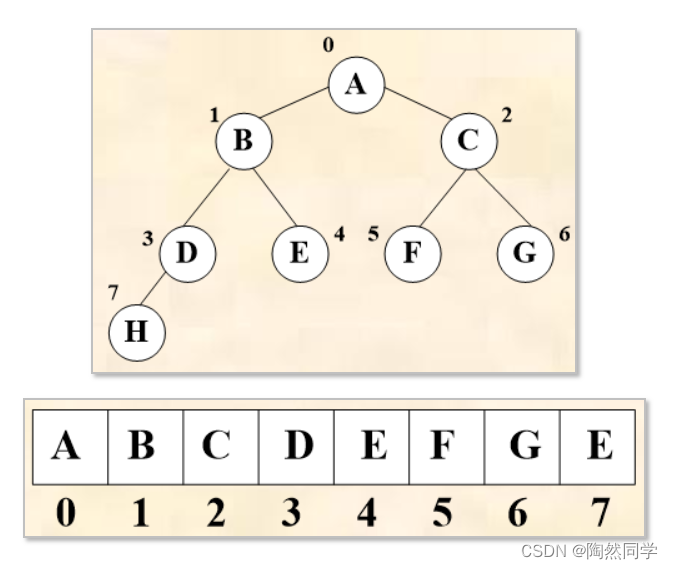
• 完全二叉树及其顺序存储

  

   

• 算法

public BiTreeNode createBiTree(String sqBiTree, int index) {
    BiTreeNode root = null;
    if(index < sqBiTree.length()) {
        root = new BiTreeNode(sqBiTree.charAt(index));
        root.lchild = createBiTree(sqBiTree, 2*index+1);
        root.rchild = createBiTree(sqBiTree, 2*index+2);
    }
    return root;
}

5.5 哈夫曼树及哈夫曼编码

5.5.1 基本概念

• 结点间路径：从一个结点到另一个结点所经历的结点和分支序列。

• 结点的路径长度：从根节点从该结点的路径上分支的数目。

• 结点的权：在实际应用中，人们往往会给树中的每一个结点赋予一个具有某种实际意义的数值，这个数值被称为该结点的权值。

• 结点的带权路径长度：该结点的路径长度与该结点的权值的乘积。

• 树的带权路径长度：树中所有叶结点的带权路径长度之和。

$$
WPL = \sum_{i=1}^{n}W_i × Li & （L_i为带权，W_i叶子结点长度）\\
$$

5.5.2 最优二叉树

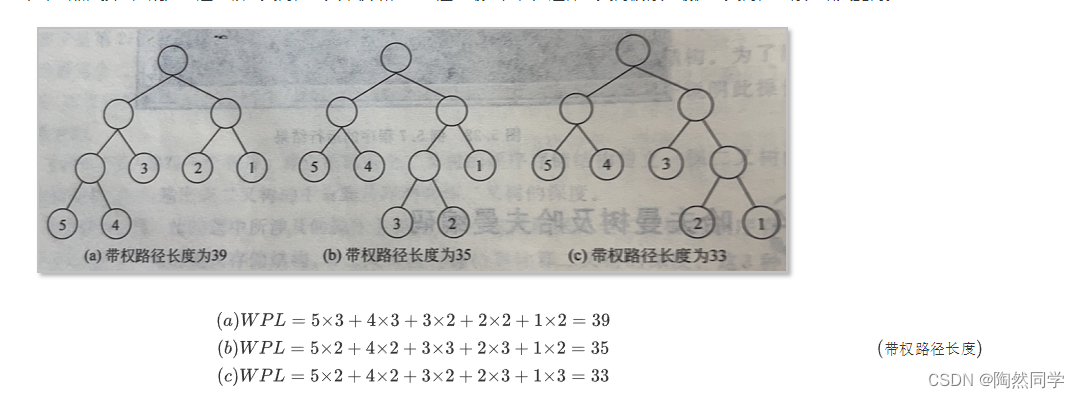
• 给定n个权值并作为n个叶结点，按一定规则构造一颗二叉树，使其带权路径长度达到最小值，则这棵二叉树被称为最优二叉树，也称为哈夫曼树。

 

$$
(a) WPL=5×3+4×3+3×2+2×2+1×2 = 39 \\ (b) WPL=5×2+4×2+3×3+2×3+1×2 = 35 \\ (c) WPL=5×2+4×2+3×2+2×3+1×3 = 33 \\ \tag {带权路径长度}
$$

• 同一组数据的最优二叉树不唯一，因为没有限定左右子树，并且有权值重复时，可能树的高度都不唯一，唯一的只是带权路径长度之和最小。 构建哈夫曼树的时候即可以推导出。

5.5.3 构建哈夫曼树

$$
(1)由已知给定的n个权值\{w_1,w_2,w_3,...,w_n\}，构建一个有n课二叉树所构建的森林 \\ F=\{T_1,T_2,T_3,...T_n\}，其中每一棵二叉树中只含一个带权值为w_i根节点，其左、右子树为空\\ \\ (2)在二叉树森林F中选取根节点的权值最小和次小的两棵二叉树，分别把它们作为左子树和右子树\\ 去构建一颗新二叉树，新二叉树的根节点权值为其左右子树根节点的权值之和。 \\ \\ (3)作为新二叉树的左右子树的这两棵二叉树从森林F中删除，同时加入刚生成的新二叉树 \\ \\ (4)重复步骤(2)和(3)，直到森林F中只剩一颗二叉树为止，该二叉树就是哈夫曼树。 \\
$$

 

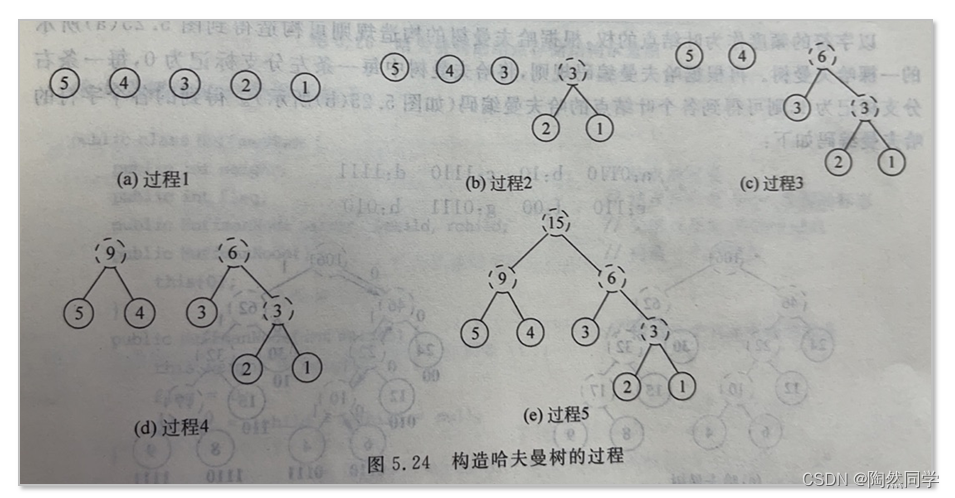
5.5.4 哈夫曼编码

• 编码诉求：对字符集进行二进制编码，使得信息的传输量最小。如果能对每一个字符用不同的长度的二进制编码，并且尽可能减少出现次数最多的字符的编码位数，则信息传送的总长度便可以达到最小。

• 哈夫曼编码：用电文中各个字符使用的频度作为叶结点的权，构造一颗具有最小带权路径长度的哈夫曼树，若对树中的每个==左分支赋予标记0，右分支赋予标记1==，则从根节点到每个叶结点的路径上的标记连接起来就构成一个二进制串，该二进制串被称为哈夫曼编码。

• 练习：p176

  已知在一个信息通信联络中使用了8个字符：a、b、c、d、e、f、g和h，每个字符的使用频度分别为：6、30、8、9、15、24、4、12，试设计各个字符的哈夫曼编码。

  0

  1

  0

  1

  0

  1

  0

  1

  0

  1

  0

  1

  0

  1

  4

  6

  8

  9

  10

  12

  15

  17

  22

  24

  30

  32

  46

  62

  106

• 哈夫曼树进行译码

  • 哈夫曼编码是一种前缀码，任何一个字符的编码都不是同一个字符集中另一个字符的编码的前缀。

  • 译码过程时编码过程的逆过程。从哈夫曼树的根开始，从左到右把二进制编码的每一位进行判别，若遇到0，则选择左分支走向下一个结点；若遇到1，则选择右分支走向下一个结点，直至到达一个树叶结点，便求得响应字符。

5.5.5 哈夫曼编码类

• 哈夫曼结点类

  public class HuffmanNode {
  ​
      public int weight;// 权值
      public int flag; // 节点是否加入哈夫曼树的标志
      public HuffmanNode parent,lchild,rchild; // 父节点及左右孩子节点
  ​
      // 构造一个空节点
      public HuffmanNode(){
          this(0);
      }
  ​
      // 构造一个具有权值的节点
      public HuffmanNode(int weight){
          this.weight = weight;
          flag=0;
          parent=lchild=rchild=null;
      }
  }

• 哈夫曼编码类

  public class HuffmanTree {
      // 求哈夫曼编码的算法，w存放n个字符的权值(均>0)
      public int[][] huffmanCoding(int[] W){
          int n = W.length;  // 字符个数
          int m = 2*n -1;   //哈夫曼树的节点数
          // 构造n个具有权值的节点
          HuffmanNode[] HN = new HuffmanNode[m];
          int i = 0;
          for (; i<n ; i++) {
              HN[i] = new HuffmanNode(W[i]);
          }
          // 创建哈夫曼树
          for (i = n;  i<m ; i++) {
              // 在HN[0...1]选择不在哈夫曼树中，且权值weight最小的两个节点min1和min2
              HuffmanNode min1 = selectMin(HN,i-1);
              min1.flag = 1;
              HuffmanNode min2 = selectMin(HN,i-1);
              min2.flag = 1;
              // 构造 min1和min2的父节点，并修改父节点的权值
              HN[i] = new HuffmanNode();
              min1.parent=HN[i];
              min2.parent=HN[i];
              HN[i].lchild = min1;
              HN[i].rchild = min2;
              HN[i].weight = min1.weight+min2.weight;
          }
          //  从叶子到根 逆向求每个字符的哈夫曼编码
          int[][] HuffCode = new int[n][n]; // 分配n个字符编码存储空间
          for (int j =0;j<n;j++){
              // 编码的开始位置，初始化为数组的结尾
              int start = n-1;
              // 从叶子节点到根，逆向求编码
              for(HuffmanNode c = HN[j],p=c.parent;p!=null;c=p,p=p.parent){
                  if(p.lchild.equals(c)){
                      HuffCode[j][start--]=0;
                  }else{
                      HuffCode[j][start--]=1;
                  }
              }
              // 编码的开始标志为-1，编码是-1之后的01序列
              HuffCode[j][start] = -1;
  ​
          }
  ​
          return HuffCode;
  ​
      }
  ​
      // 在HN[0...1]选择不在哈夫曼树中，且权值weight最小的两个节点min1和min2
      private HuffmanNode selectMin(HuffmanNode[] HN, int end) {
          // 求 不在哈夫曼树中， weight最小值的那个节点
          HuffmanNode min = HN[end];
          for (int i = 0; i < end; i++) {
              HuffmanNode h = HN[i];
              // 不在哈夫曼树中， weight最小值
              if(h.flag == 0 && h.weight<min.weight){
                  min = h;
              }
          }
          return min;
      }
  ​
  ​
  }

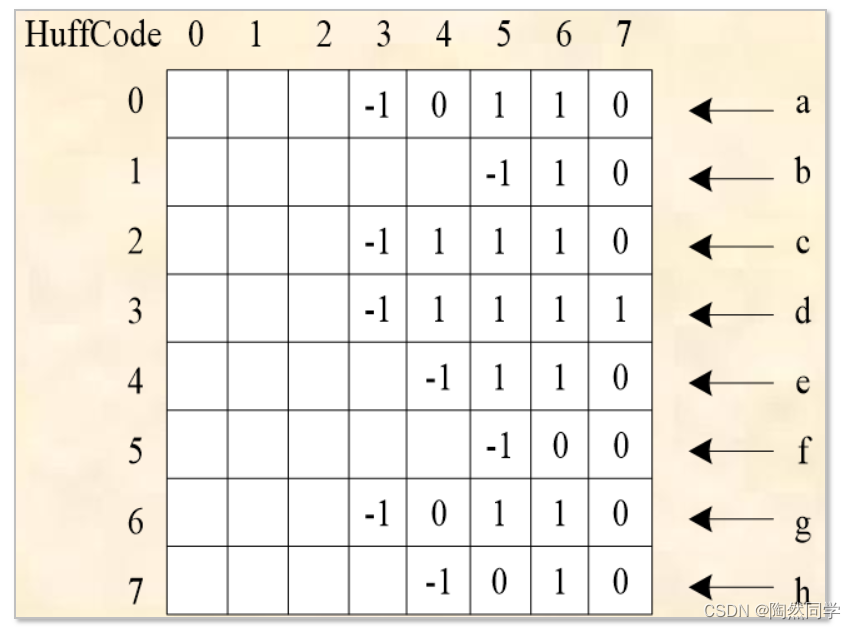
• 哈夫曼编码会用类似如下格式进行存储

  

   

• 测试类

  public class Demo02 {
  ​
      public static void main(String[] args) {
          // 一组权值
          int[] W = {6,30,8,9,15,24,4,12};
          // 创建哈夫曼树
          HuffmanTree tree = new HuffmanTree();
          // 求哈夫曼编码
          int[][] HN = tree.huffmanCoding(W);
          //打印编码
          System.out.println("哈夫曼编码是： ");
          for (int i = 0; i < HN.length; i++) {
              System.out.print(W[i]+" ");
              for (int j = 0; j < HN[i].length; j++) {
                  if(HN[i][j] == -1){
                      for (int k = j+1; k <HN[i].length ; k++) {
                          System.out.print(HN[i][k]);
                      }
                      break;
                  }
              }
              System.out.println();
          }
      }
  }