做题笔记

8.11

没事干，只能板刷CF2000了。

CF2126F

一棵树，点有颜色，边有边权，若一条边所连接的两点颜色相同，则这条边贡献为 \(0\)。每次修改一个点的颜色，求总贡献。

简单题。考虑修改后对父亲和儿子的影响。若原本的颜色与父亲相同，\(ans\) 加上到父亲的边权；若新的颜色与父亲相同，ans减去到父亲的边权。儿子同理。

CF2114F

给定 \(x,y,k\)，每次可以选定一个 \(1\leq n\leq k\)，使 \(x \leftarrow x\times n 或 \frac{x}{n}\)，求 \(x\) 变成 \(y\) 的最小操作次数。

DP妙妙题。令 \(a=\frac{x}{\gcd(x,y)},b=\frac{y}{\gcd(x,y)}\)。问题转换为用若干个 \(\leq k\) 的整数乘出 \(a\) 和 \(b\)，使使用的数最少。记搜可做。
T了。加入一行妙妙优化：

if(n<=k)return f[n]=1;

A了。感性证明：若 \(k\) 比较大，显然优化明显。若 \(k\) 比较小，搜索树的节点数一定不多。猜测复杂度 \(O(\sqrt{\max(a,b)})\)。
太tang妙了。

P13565

n个数，最多m次操作，每次操作可以把一个数 \(\times 2\)，问或和最大值。

贪心。\(ans\) 的位数肯定与序列最大值的位数相同。考虑从最高位向下枚举，每一位都判断是否能在 \(m\) 次内将所有数的这一位变成 \(0\)。注意不能改变之前的答案。

CF1805D

给定一棵 \(n\)（\(2\leq n\leq 10^5\)）个节点的无根树，对于每个 \(k\)（\(1\leq k \leq n\)），定义一个无向图 \(G_k\)，其中由边连接的两个节点 \(u\) 和 \(v\) 的距离至少为 \(k\)。请你计算 \(G_k\) 的连通块个数。

树的直径性质题。令 \(dis_i\) 表示 \(i\) 到树上距离最远的点的距离(必然是树的直径的两个端点中的一个)，可以 \(2\) 次 \(dfs\) 求出直径，再 \(1\) 次统计答案。

8.12

已完成今日 Ynoi 大学习。

P5072

给你一个序列，每次查询一个区间 \([l,r]\) 中所有子序列分别去重后的和\(\mod p\)。

所谓Ynoi简单题，对我而言不可战胜。
首先莫队是显然的。考虑一个数 \(a_i\)，它在一个长度为 \(n\) 的序列中出现了 \(x\) 次，则它对答案的贡献为 \((2^n-2^{n-x})a_i\)。
证明：总子序列数量-不包含 \(a_i\) 的。
然后考虑统计每种数的出现次数 \(cnt\)，和每种出现次数的数的和 \(sum\)。
不难证明只会有 \(\leq \sqrt{n}\) 种不同的 \(cnt\)。可以链表维护。
发现 \(2\) 的幂次不好算，使用神秘分块算出 \(2^0,2^1\dots 2^{\sqrt{n}}\) 和 \(2^{\sqrt{n}},2^{2\sqrt{n}}\dots 2^n\)，然后凑答案。
不难发现复杂度为 \(O(m\sqrt n)\)。

8.13

继续完成今日 Ynoi 大学习。

P5046

强制在线的区间逆序对，\(n,m\leq 10^5\)。

维护 \(ansL_{i,j}\) 表示 \(j\) 到 \(i\) 块块尾的逆序对个数，\(ansR_{i,j}\) 表示 \(j\) 到 \(i\) 块块首的逆序对个数。再加上其他的一些东西，容斥一下就可以把答案求出来。
具体而言，整块用上面的东西选出来，散块可以用类似于归并的方法算。
卡常严重。难写死了>_<。

8.14

并未完成今日 Ynoi 大学习。

P4069

一棵树，两个操作，修改每次在一条路径上打一个一次函数的 \(tag\)，查询一条路径上函数值的最小值。\(n,m\leq 10^5\)。

一眼树剖+李超，考虑将 \(i\) 到根节点的距离 \(dis_i\) 设为横坐标，这样一条重链上的横坐标是递增的。写出式子：

\[ans=\max \{k\times dis_{ s\rightarrow i} +b\} i\in\{s \dots t\} \]

令 \(p=LCA(s,t)\)，把式子拆开：

\[\begin{align} ans&=\max \{-k\times dis_i+k\times dis_s +b\} i\in\{s \dots p\}\\ &=\max \{k\times dis_i + k\times(dis_s-2\times dis_p)+b\} i\in\{p \dots t\} \end{align} \]

然后就可以愉快的李超了~
李超好难写>_<。

CF1311D

给定三个整数 \(a,b,c\)，每次可以将他们中的一个 \(+1\) 或 \(-1\)，求最少操作次数使得 \(0< a\leq b\leq c\) 且 \(a|b,b|c\)， \(T\leq 100，a,b,c\leq 10^4\)。

萌萌题。预处理出所有 \(10^4\) 以内的数的因数，然后枚举 \(b\)，求 \(c\) 是平凡的，求 \(a\) 可以二分 \(b\) 的所有因子。

8.15

不想完成今日 Ynoi 大学习，因为马上就可以滚回我忠诚的CQ了。
象征意义切两道水题。
煞笔模拟赛给我去死。

P9464

题意很长，不写了。
不难发现两块奖牌被发给同一个人后，这两块奖牌的路径就会完全相同。考虑用树结构维护。每次把代表 \(x_i\) 和 \(y_i\) 的奖牌的子树合并到新节点上面，就可以统计答案了。

CF859C

一个序列，两个人从左到右依次取数。每次可以做两个操作：

• 把这个数给被人，自己保留下个数的决策权。
• 把这个数给自己，决策权给被人。

求两人的最大得分。

巴巴博弈DP。令 \(f_i\) 表示当前扫描到 \(i\)，先手的最大得分。注意我们要倒序枚举，因为正序的话我们无法确定抉择权的变化。
若先手选择第 \(1\) 种，\(f_i\) 可以直接继承 \(f_{i+1}\)。
若先手选择第 \(2\) 种，\(f_i=sum-f_{i+1}+a_i\)。

8.19

回CQ颓了几天，然后注意到没有完成今日 Ynoi 大学习。
但是先等等。

P5954

考虑把每个点的贡献分成两部分。\(f_u\) 表示 \(u\) 发生后可以推导出要发生的事件。\(g_u\) 表示 \(u\) 发生可以反推出必然发生的事件并上 \(f_u\)。对于 \(u\) 的所有前驱 \(v\)，只有在所有 \(g_v\) 的交集中出现的事件才必然发生。
反正可以 bitset 乱搞。

P1450

好吧我对容斥一窍不通，还是后面再来填坑吧。

8.22

咕了昨天的模拟赛，今天在补题。

T1

一个 \(a\times b\) 的棋盘，在 \((c,d)\) 处有一个棋子，可能是车、马、象中的一个。现在要让它移动 \(e\) 步，问有多少种不同的路径。\(a\times b \leq 100，e\leq 10^9\)。

考虑 \(e\leq 10^4\) 的情况。记 \(f_{i,j,k}\) 表示从 \(i\) 出发，走 \(j\) 步到 \(k\) 的方案数。可以 bfs 填表。\(j\) 可以滚掉。
发现对于每一层，填表的方式都是相同的。于是参考 P2886 的思路做矩阵快速幂。

T2

给定一个字符串以及哈希进制 \(p\) 与模数 \(m\)，问有多少对子串哈希冲突。\(n\leq 3000\)。

冲突数=哈希值相同-子串相同。哈希值相同的子串可以模拟，子串相同可以对每个后缀做 KMP，或者 SAM。但我只想写哈希。
艹，卡 map 食人？
艹，卡哈希？
被迫写了双哈希。

T3

给定一个长度为 \(n\) 的序列 \(a\)，问有多少区间 \([l,r]\) 满足 \(a_l\oplus a_{l+1}\dots a_r \leq \max\{a_l,a_{l+1}\dots a_r\}\)。\(n\leq 10^5\)。

统计点对数量，考虑 CDQ （我真不知道是怎么想到的）。考虑最大值在左边的情况，从 \(mid\) 开始向左枚举，统计后缀最大值和后缀异或和，然后把右边小于后缀最大值的全插入 trie ，统计 trie 树上所有满足 异或后缀异或和后小于等于后缀最大值的数的个数。右边同理。

8.23

Ynoi 是什么？

P5495

给定一个长度为 \(n\) 的数列 \(a_1,a_2,a_3,\dots,a_n\)。现在你要求出一个长度为 \(n\) 的数列 \(b_1,b_2,b_3,\dots,b_n\)，满足

\[b_k=\sum_{i|k}a_i \]

\(n\leq 2\times 10^7\)。

狄利克雷前缀和板子。令 \(i=a_1^{b_1}\times a_2^{b_2}\dots a_k^{b_k}\)，\(j=a_1^{c_1}\times a_2^{c_2}\dots a_k^{c_k}\)。\(a_i\) 对 \(b_j\) 有贡献，当且仅当 \(\forall b_i\leq c_i\)。发现这可以高位前缀和维护。令 \(f_i\) 表示所有满足 质因数分解后指数都不大于 \(i\) 的指数的 \(j\) 对应的 \(a_j\) 的和。

8.25

P6442

给定 \(n\) 个篮子，共有 \(m\) 种玩具，第 \(i\) 个篮子里面有 \(k_i\) 个玩具。现要选取若干个篮子，使其中玩具的并集大小为 \(m\)，求方案数。\(n\leq 10^6\)，\(m\leq20\)。

求并集为全集的方案数，取反后转为求交集为空的方案数。令 \(f_i\) 表示 \(i\) 是多少篮子的子集，\(g_i\) 表示 \(i\) 是多少篮子的交集的子集。
显然 \(g_i=2^{f_i}-1\)。（因为若i既是A的子集也是B的子集，则i一定是 \(A\cap B\) 的子集。
\(f_i=\sum_{i\subseteq j} a_j\)，可以 sos dp。
考虑容斥以统计答案。全集为 \(g_0\)，若 \(i\) 有奇数个 \(1\) ，则需要从答案中减去 \(g_i\)，否则加上 \(g_i\)。

CF165E

给定 \(n\) 个整数，对于每个整数 \(a_i\) 找到一个 \(j\) 满足 \(a_i \& a_j=0\)，输出 \(a_j\)。

\(a_i\& a_j = 0 \iff a_j\subseteq \neg a_i\)。令 \(f_i=b\) 表示 \(i\) 的子集 \(b\) 在 \(a\) 中出现过。

P5017

给定一条数轴，上面有一些可重点。要数轴上布置若干段长度为 \(m\) 的区间，使每个点到距它最近的区间右端点的距离和最小。数轴长度 \(\leq 4\times 10^6\)。

令 \(f_i\) 表示将 \((0,i]\) 进行分段，且 \(i\) 为最后一段的结尾，距离最小值。显然有 \(f_i=\min_{j\leq i-m}\{f_j+\sum_{j<t_k\leq i}i-t_k\}\)。暴力转移复杂度 \(O(t^3)\)。
考虑运用前缀和。\(cnt_i\) 表示 \((0,i]\) 有多少个点，\(sum_i\) 表示 \((0,i]\) 中每个点到原点的距离和。\(f_i=\min_{j\leq i-m}\{f_j+(cnt_i-cnt_j)\times i-(sum_i-sum_j)\}\)。转移复杂度 \(O(t^2)\)。
发现 \(j\) 取在 \((i-2m,i-m]\) 时一定不劣，所以可以改写为 \(f_i=\min_{i-2m<j\leq i-m}\{f_j+(cnt_i-cnt_j)\times i-(sum_i-sum_j)\}\)，复杂度 \(O(tm)\)。我觉得能过。

8.26

P1155

两个栈，支持从输入序列插入和弹出至输出序列。现要将输入序列升序排序，求方案。\(n\leq 1000\)。

先考虑一个栈的情况。一个序列无法被排成升序，当且仅当存在 \(i<j<k\) 满足 \(a_k<a_i<a_j\)。我们设 \(suf_i=\min\limits_{j=i}^na_i\)，若 \(i<j\) 满足 \(suf_{j+1}<a_i<a_j\)，则 \(i,j\) 不能共存，就建一条双向边，后面跑二分图。输出答案就模拟一下。

P1315

一条数轴上面有 \(n\) 个站点，第 \(i-1\) 站与第 \(i\) 站之间距离为 \(d_i\)，有 \(m\) 个人要等车，其中第 \(i\) 个人会在 \(t_i\) 时到达 \(a_i\) 站并坐车前往 \(b_i\) 站。车只有一辆，会在 \(0\) 时刻出现在 \(1\) 号车站。车到达 \(i\) 站后，需要等所有会在 \(i\) 站上车的乘客上车后才会前往 \(i+1\) 站。\(k\) 次机会，每次将一个 \(d_i-1\)（满足 \(d_i\geq 0\)）。问总的乘客旅行时间最小值。\(n\leq10^3,m\leq10^4,k\leq 10^5\)。

令 \(latest_i\) 表示所有 \(i\) 站上车的乘客中最晚到达的时间，\(arrive_i\) 表示车到达 \(i\) 的最早时间。则有递推式 \(arrive_i=\max(arrive_{i-1},latest_{i-1})+d_i\)。
若选择对 \(d_i-1\)，对于 \(j\geq i\)，若 \(arrive_i\geq latest_i\)，\(arrive_i\) 会 \(-1\)。否则不应修改，且应该跳出循环。对于所有 \(k\) 次操作都去如上模拟。

8.27

P3435

开始填之前留下的坑。

对于字符串 \(A\) 的一个真前缀 \(Q\)，若 \(A\) 是 \(QQ\) 的前缀，则称 \(Q\) 是 \(A\) 的周期。对于 \(A\) 的所有前缀，求它的最长周期的长度和。\(n\leq10^6\)。

令 \(A\) 长度为 \(n\)，\(Q\) 长度为 \(m\)，则 \(A_{1\dots n-m}=Q_{1\dots n-m}=A_{m+1\dots n}\)。要使 \(m\) 最大，我们需要找到最小的 \(k\)，满足 \(A_{1\dots k}=A_{n-k+1\dots n}\) 且 \(k>0\)。
使用 KMP 算法，从 \(next_i\) 开始递推，直到 \(next_j=0\)，\(j\) 即为最小匹配长度，同时将 \(next_i\) 更改为 \(j\)，以后递推到 \(i\) 时就可以直接返回 \(j\)。

P5021

给定一棵 \(n\) 个点带边权的树，要把树拆成 \(m\) 条链，使最短的一条链长度最大。\(m\leq n\leq 5\times 10^4\)。

二分答案，看长度 \(\geq mid\) 的链能不能有 \(m\) 条。
考虑贪心。假设当前遍历到 \(u\)，\(u\) 子树已经统计了答案。\(u\) 的贡献有两种：两个端点都在子树中 或 一个端点在子树中，另一个端点是 \(u\) 的祖先。发现 \(u\) 只能向祖先贡献一条来自子树的链，所以所有儿子应该尽量匹配，然后把剩下的最长链上传。

8.27

模拟赛赛时笔记

T1(CF1011F)

一棵二叉树，叶子节点有权值（\(0\) 或 \(1\)），其他节点把两个子节点的值做位运算得到自己的值。问每个叶子节点 \(\oplus 1\) 后节点 \(1\) 的结果，询问相互独立。\(n\leq 3\times 10^5\)。

递推。先来一遍统计每个节点在不改变叶节点时的权值，然后我们令 \(f_{u,0/1}\) 表示表示 \(u\) 输出 \(0/1\) 时 \(1\) 节点的结果。起点 \(f_{1,0}=0,f_{1,1}=1\)。对于每个节点，我们拿它和它的兄弟做位运算，得到应该继承 \(f_{fa,0}\) 或 \(f_{fa,1}\)。查询时直接调用即可。
只会T1，比较菜。

8.29

P10967

一条数轴，数轴上有 \(n\) 个点，要把其中 \(m\) 个点变成特殊点，求每个点到特殊点的距离和最小值。\(n\leq300\)。

令 \(f_{i,j}\) 表示在前 \(i\) 个点中布置了 \(j\) 个特殊点的最小距离和。则可以列出转移 \(f_{i,j}=\min_{0\leq k<i}\{f_{k,j-1}+w_{k+1,i}\}\)。其中 \(w_{i,j}\) 表示区间 \([i,j]\) 中布置一个特殊点的最小距离和。发现特殊点布置在区间的中点一定最优，于是有转移方程 \(w_{i,j}=w_{i,j-1}+a_j-a_{\frac{i+j}{2}}\)。复杂度 \(O(n^3)\)。

8.31

P5514

\(n\) 个整数，把它们分成若干组，每组的权值定义为组内元素的异或和，做所有组的权值之和的最小值。\(n\leq 10^6\)。

大胆猜测最优分组方案是所有元素分一组，因为对于 \(\forall a,b\)，满足 \(a\oplus b\leq a+b\)。

P5535

\(n\) 个人，编号 \(2\) 到 \(n+1\)，若编号 \(i\) 个人得到了消息，他会在第二天把消息告诉所有编号为 \(j\) 的人，满足 \(\gcd(i,j)=1\)。在第 \(0\) 天把消息告诉编号为 \(k\) 的人，问第几天所有人都知道了消息。\(k\leq n\leq 10^{14}\)

前置知识：伯特兰-切比雪夫定理：对于所有大于 \(1\) 的整数 \(n\)，存在一个质数 \(p\)，符合 \(n < p < 2n\)。
分两种情况讨论。

• 若 \(k\) 是质数，再分两种情况。
  1、若 \(2\sim n+1\) 中没有 \(k\) 的倍数，即 \(\lfloor\frac{n+1}{2}\rfloor<k<n\)，显然只需一天。
  2、否则，因为所有非 \(k\) 的倍数的数都知道，而 \(\gcd(mk-1,mk)=1,m\geq 2\) 显然成立，所以只需两天。
• 若 \(k\) 不是质数，根据伯特兰-切比雪夫定理定理，一定有质数 \(p\) 满足 \(\lfloor\frac{n+1}{2}\rfloor<p<n\)，且因为 \(k\leq n\)，所以 \(k\) 没有满足 \((\lfloor\frac{n+1}{2}\rfloor,n)\) 的因子。此时变成第一种情况。

9.1

P1414

给定 \(n\) 个整数，询问 \(q=1\sim n\)，表示从 \(n\) 个数中选出 \(q\) 个，使它们的 \(GCD\) 最大，输出最大值。\(n\leq 10^4,inf\leq 10^6\)。

令 \(ans_i\) 表示 \(q=i\) 时的答案，\(cnt_i\) 表示 \(i\) 的出现次数。对于每个 \(1\leq i\leq inf\)，令 \(res\) 代表所有 \(\leq inf\) 的 \(i\) 的倍数的 \(cnt\) 之和，并将 \(ans_res\) 与 \(i\) 取 \(\max\)。
注意做完上述操作后对 \(ans\) 做一次后缀最大值。

P1315加强

一条数轴上面有 \(n\) 个站点，第 \(i-1\) 站与第 \(i\) 站之间距离为 \(d_i\)，有 \(m\) 个人要等车，其中第 \(i\) 个人会在 \(t_i\) 时到达 \(a_i\) 站并坐车前往 \(b_i\) 站。车只有一辆，会在 \(0\) 时刻出现在 \(1\) 号车站。车到达 \(i\) 站后，需要等所有会在 \(i\) 站上车的乘客上车后才会前往 \(i+1\) 站。\(k\) 次机会，每次将一个 \(d_i-1\)（满足 \(d_i\geq 0\)）。问总的乘客旅行时间最小值。\(n,m\leq10^5,k\leq 5\times 10^6\)。

我们规定，若 \(i\) 满足 \(arrive_i\leq latest_i\)，则称 \(i\) 为一个断点。不难发现某一时刻一定选用两个断点间的第一个路段使用加速器，并且该区间的 \(off\) 之和一定最大。
发现若选定了最优路段，则一定会对该路段不断地操作，直到该区间多出来一个断点。对 \(arrive-latest\) 建立线段树。用堆存储每一个区间，按照 \(off\) 之和排序。每次取出堆顶，设左右断点分别为 \(l,r\)，线段树求出 \(min\) 和 位置 \(pos\)，\((l,r]\) 全体减 \(min\)，将 \((l,p]\) 和 \((p,r]\) 入堆。
写不出来，悲。

9.2

P4139

定义 \(a_0=1,a_n=2^{a_{n-1}}\)，可以证明 \(b_n=a_n\bmod p\) 在某一项后都是同一个值，求这个值。

由扩展欧拉定理，\(2^{2^{2^{2^{\dots}}}\mod \phi(p)+\phi(p)}\equiv 2^{2^{2^{2^{\dots}}}}\pmod p\)。
递归处理，每次求一层的 \(2^{2^{2^{2^{\dots}}}\mod \phi(p)+\phi(p)}\)。
复杂度 \(O(p)\)。

P1290

两个数，两个人，每次将大的那个数减掉小的那个数的倍数，减成 \(0\) 获胜。问先手必胜还是后手必胜。

设两个数为 \((a,b)\) 且 \(a\leq b\)。\(a=b\) 时显然先手必胜。令 \(a=k\times b+c(c<b)\)。

• 若 \(k>1\)，先手可以把 \(a\) 变成 \(a-b,a-2b,\dots a-kb\)。其中，若 \((b,c)\) 先手必败，显然转移到 \((b,c)\)。若 \((b,c)\) 先手必胜，可以转移到 \((b+c,b)\)，后手就只能转移到 \((b,c)\)。
• 若 \(k=1\)，转移到 \((b,c)\)。

9.3

P1315加强

写不出来的原因是因为一个区间中可能有多个 \(min\) 值。令当前处理的区间为 \([l,r]\)，每次找到 \([l,r]\) 中第一个 \(min\) 的位置 \(pos\)，然后把 \(l\) 移到 \(p+1\)。可以证明复杂度是对的。
调不出来。
线段树写错了。

9.8

ABC422D

设 \(N\) 为正整数。将长度为 \(2^N\) 的非负整数序列 \(A=(A_ 1, A_ 2, \dots, A_ {2^N})\) 的不平衡值定义为通过以下运算得到的非负整数值：

• 最初，设置 \(X=0\) 。
• 执行以下一系列操作 \(N\) 次：
  • 将 \(X\) 更新为 \(\max(X, \max(A) - \min(A))\) ，其中 \(\max(A)\) 和 \(\min(A)\) 分别表示序列 \(A\) 的最大值和最小值。
  • 将开头的元素两两配对，并排列它们的和，形成一个长度为开头一半的新序列。即设置 \(A \gets (A_ 1 + A_ 2, A_ 3 + A_ 4, \dots, A_ {\vert A \vert - 1} + A_ {\vert A \vert})\) 。
• 最后的值 \(X\) 就是不平衡值。
  已知 \(\sum A_i=k\)，求构造 \(A\) 是不平衡值最小。
  \(n\leq 20\)。

若不平衡值 \(\geq 2\)，显然可以通过调整使它小于 \(2\)。所以不平衡值只能是 \(0\) 或 \(1\)。
当 \(2^n|k\) 时，不平衡值为 \(0\)。否则为 \(1\)。

ABC422E

平面直角坐标系中有 \(n\) 个点（ \(n\) 是奇数），求一条穿过大于 \(\frac{n}{2}\) 个点的直线 \(ax+by+c=0\)，输出 \(a,b,c\)。\(n\leq 5\times 10^5\)。

因为有一半的点在同一条直线上，所以枚举两个点只有 \(\frac{1}{4}\) 的概率不满足条件。
于是随机两个点确定一条直线，\(O(n)\) 判断。

ABC422F

\(n\) 个点 \(m\) 条边的无向图，第 \(i\) 条边的边权定义为走 \(i\) 之前经过的点权的前缀和，对于 \(ed=1\sim n\)，求 \(1\) 到 \(ed\) 的最短路长度。\(n,m\leq 5000\)。

令 \(f_{i,j}\) 表示走到 \(i\)，还需要走 \(j\) 步到终点的最短路长度。起点 \(f_{1,j}=0(0\leq j\leq n)\)，其余为 \(inf\)。\(j\) 从 \(n\) 到 \(1\)，每次转移到下一层。

9.12

P1600

题面太长了。

dsu。维护一个 \(map_i\) 表示当前遍历过的所有点中深度为 \(i\) 的起点的个数。设遍历到 \(u\)，\(u\) 子树中有一个起点 \(v\)，若 \(w_u=dep_v-dep_u\)，则 \(v\) 出发的人可以被 \(u\) 观测到。终点的统计同理。
注意到若 \(lca(s,t)\) 可以观测到 \(s\)，则它一定可以观测到 \(t\)。所以先统计起点到 \(u\) 的答案，再删去所有满足 \(lca(s,t)=u\) 的 \((s,t)\) 对的 \(s\)，再统计终点到 \(u\) 的答案。最后删去 \(t\)。

以上解法是错误的。

9.13

\(n\) 个数对 \((a,b)\)，每对选一个，求 \(a\) 的最大值和 \(b\) 的最大值之差的绝对值的最大值和最小值。

按 \(a\) 升序排序，枚举 \(i\) 确定 \(a\) 的最大值。首先 \([i+1,n]\) 的 \(b\) 显然要选。然后若 \(\max(b_{i+1}\dots b_n)< a_i\)，找到 \([1,i-1]\) 中的 \(b\) 中 \(a_i\) 的前驱后继，统计答案。

9.25

P13520

有 \(n\) 个箱子，每个箱子有体积 \(s_i\) 和容积 \(c_i(s_i>c_i)\)。能把箱子 \(i\) 装进箱子 \(j\) 中当且仅当 \(s_i<c_j\) 且 \(j\) 中没有其他箱子，但 \(i\) 中可以有箱子。定义存放箱子的成本，等于没有被装在任何其他箱子里的箱子的数量。对于 \(i=1\sim n\) 求出存放 \(1,2,3\dots i\) 号箱子的最小成本。

考虑将体积视为一条数轴，则箱子可以表示为数轴上的一个区间。两个箱子互斥，即不能放入另一个，当且仅当交集不为空。可以线段树做。

9.26

P7077

题面

考虑一个没有操作3的做法：从后往前统计每个操作1之后所有操作2的积，也就是操作1的系数，最后累加起来。
我们把操作1、2视为叶节点，操作3的调用视为建边。定义 \(mul_u\) 表示表示假设在 \(u\) 的所有子函数后添加一个加 \(1\) 操作，它的系数是多少。\(mul_u\) 的值等于 \(fa_u\) 后面的所有兄弟的 \(mul\times\) \(u\) 后面的所有兄弟的 \(mul\)。可以通过两遍拓扑排序计算。

10.5

P13744

给定一个长度为 \(n\) 的序列 \(a_1,a_2\dots a_n\)，\(q\) 次询问，每次给定一个长度为 \(m\) 的序列 \(b_1,b_2\dots a_m\)，询问序列 \(b\) 是否是 \(a\) 的子序列。\(n,m,q,a_i,b_i\leq 10^6,\sum m\leq10^6\)。

对于每个数值，开个 \(vector\) 存它在 \(a\) 中的位置。定义 \(last\) 表示当前匹配到 \(a\) 的最后一位。对于 \(i=1,2\dots m\)，从 \(vector_{b_i}\) 中 \(upper\_bound\) \(last\) 的位置。

10.9

P10950

有一个长为 \(m\) 的环，值都是 \(0\) 或 \(1\)，要求所有连续个长为 \(k\) 的子串互不相同。现在已知 \(k\)，求 \(m\) 的最大值和字典序最小的方案。

首先不同的子串个数最多为 \(2^k\)，而每个不同子串对环长的贡献为 \(1\)。所以 \(m=2^k\)。
然后构造一个如下样式的自动机，每一个节点表示最后 \(k-1\) 位是什么。

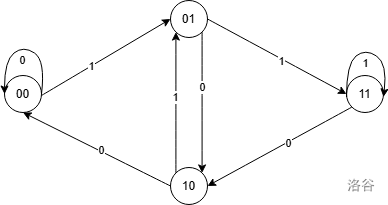
然后就可以 dfs 了。

10.12

P6069

\(n\) 个数，每次可以修改一个数，最终使方差不大于 \(m\)，求最小修改次数。
为方便，\(m\) 为实际方差的 \(n\) 倍。

首先要求 \(\sum (a_i-p)^2\leq m\)，即求 \(n\times \sum a_i^2-(\sum a_i)^2 \leq nm\)。
显然，最优的保留序列一定是在数值上连续的一段，对于不保留的，将他们修改成保留的这一段的平均值，这样就不会对答案产生影响。
二分答案即可。

10.14

P14201

给定一个长度为 \(n\) 的序列 \(A\) 与 \(m\) 组 \(l_i,r_i\)。
要构造一个长度为 \(k\) 的序列 \(B\)，记 \(f_i=\operatorname{mex}(A_{l_i},A_{l_i+1},\dots,A_{r_i},B_1,B_2,\dots,B_k)\)。那么有：\(f_i(1 \le i \le m)\) 相等。
对于 \(k=0,1,\dots ,n\)，求在所有满足条件的 \(B\) 中，\(f_i\) 值最大是多少。若不存在任何一个 \(B\)，则最大值为 \(-1\)。

考虑枚举 \(mex\)。设当前枚举的 \(mex\) 为 \(i\)，\(B\) 的大小为 \(sz\)。接下来分三种情况讨论。

• \(i\) 至少在一个区间中出现了。此时 \(i\) 不能做答案，同时需要消耗 \(1\) 的容量在 \(B\) 中放入 \(i\)。
• \(i\) 在所有区间中出现了。此时 \(i\) 不能做答案，\(B\) 不需要更改。
• \(i\) 未在任何一个区间中出现。此时 \(i\) 可以做答案，同时需要消耗 \(1\) 的容量在 \(B\) 中放入 \(i\)。

\(1\) 和 \(3\) 是简单的，可以差分。难点在 \(2\)。
考虑双指针+ set 统计所有区间的值域的交集。需要排序。
我们希望不存在互相包含的区间，所以我们按右端点升序排序，右端点相同就按左端点降序。
去重时，如果新的区间左端点大于去重数组最后一个区间的左端点，就将该区间加入去重数组。
可以证明这样排序是正确的。