线性代数--二次型
二次型化为矩阵表达式
二次型:每项的幂都是2
二次型的矩阵一定是对称的
矩阵A:二次型的矩阵

标准型
只有平方项叫做标准型 平方项的系数可以取零
线性替换
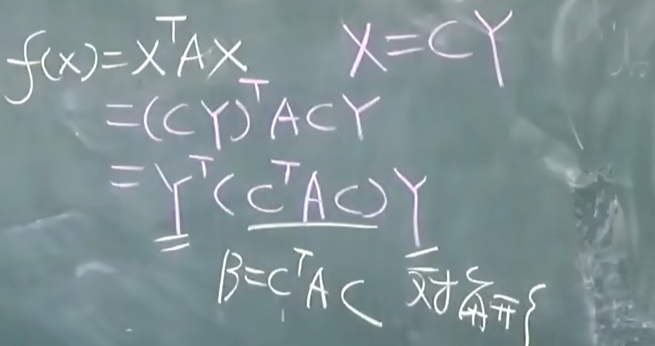
X=CY 线性替换
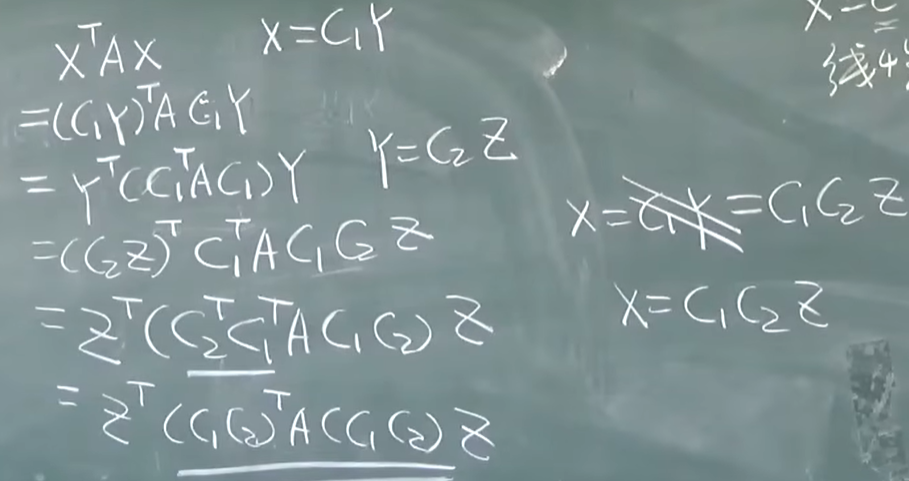
定理:
- 二次型经过线性替换之后仍然是新的二次型的矩阵 仍然是对称的
![image]()
合同
- 性质
- 反身性
![image]()
- 对称性
![image]()
- 传递性
![image]()
- 矩阵左乘可逆矩阵或右乘可逆矩阵秩不变
![image]()
![image]()
![image]()
![image]()
矩阵的关系

化二次型为标准型
有三种方法:
- 配方法
![image]()
还有一步:
![image]()
只有交叉项的配方:
有三个变量令:
![image]()
有四个变量令:
![image]()
然后带入原式,再用配方 - 初等变换
![image]()
![image]()
![image]()
- 正交替换
![image]()
规范型

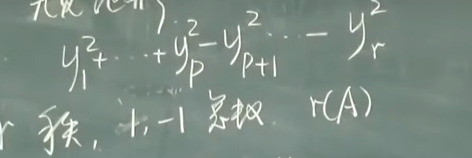
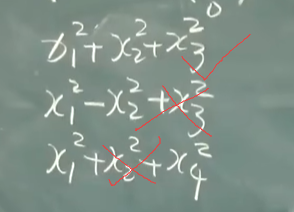
- 正向个数叫正惯性指数
- 负向个数叫负惯性指数
- 相减叫符号差
有定性
- 有定的
![image]()
- 不定的
![image]()
![image]()
有定性的判别
- 正定二次型如果经过一次线性替换以后,仍是正定
![image]()
![image]()
顺序主子式

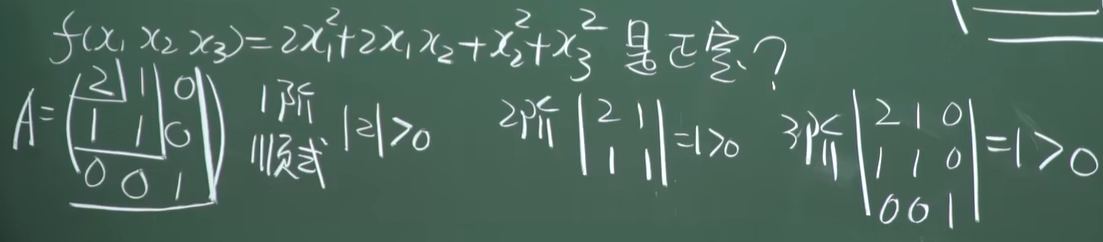
正定性质
- A正定 A逆正定
- A正定 A伴随正定
- A正定 A的k次方也正定
- A正定 B半正定 A+B正定
![image]()
- A正定 A的主对角元素大于0

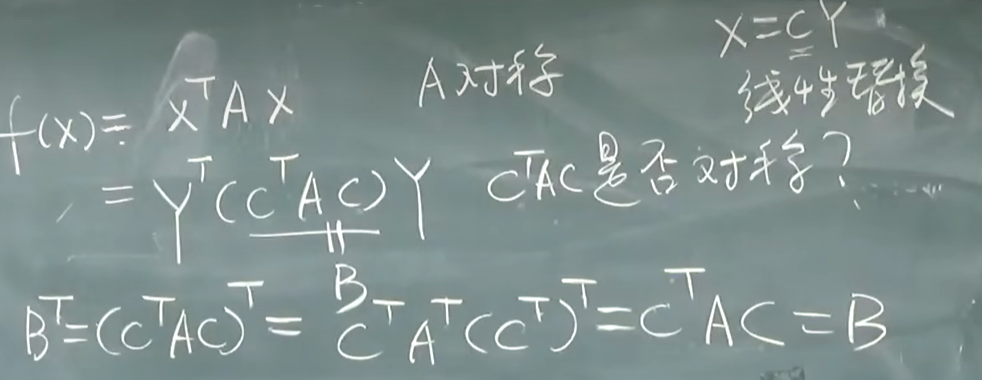


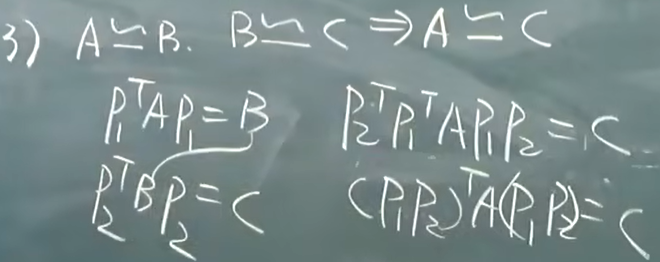
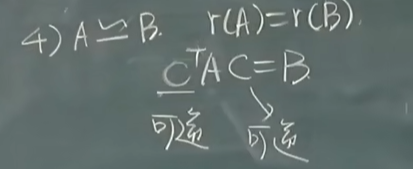
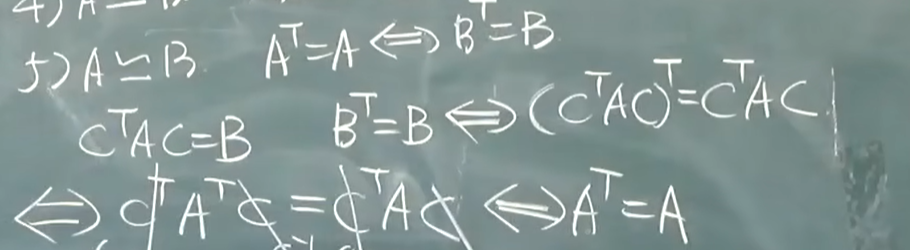
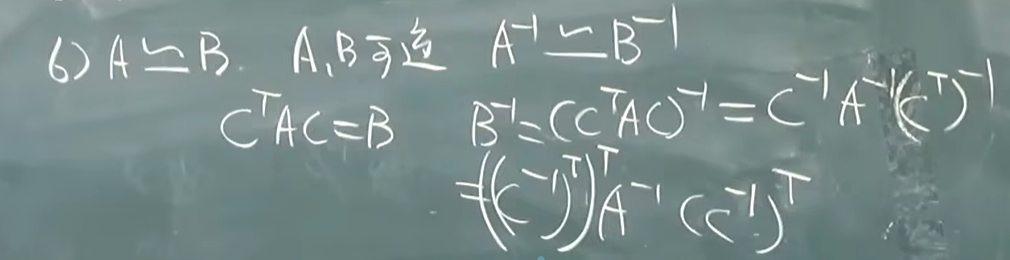

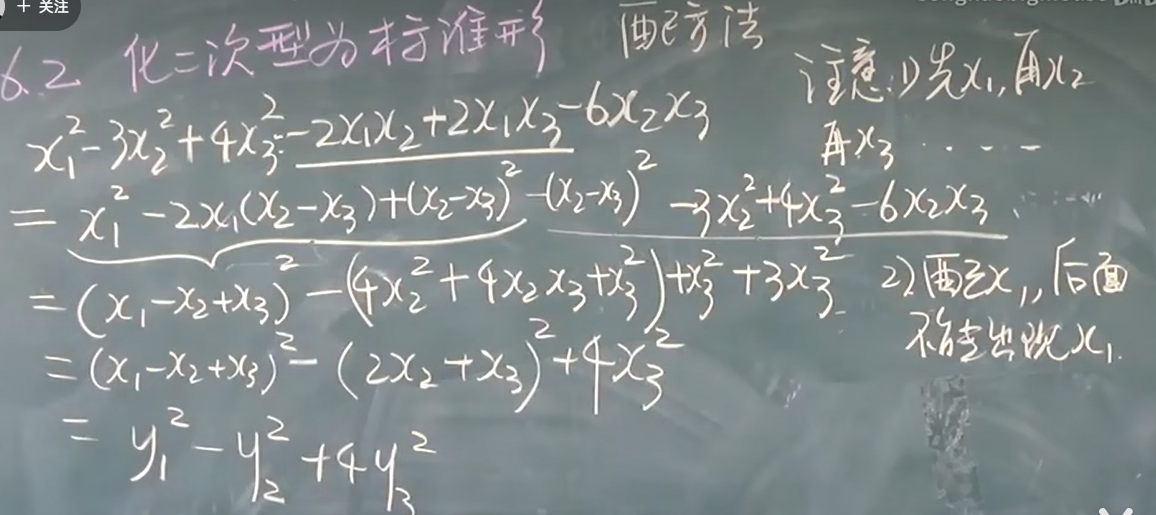
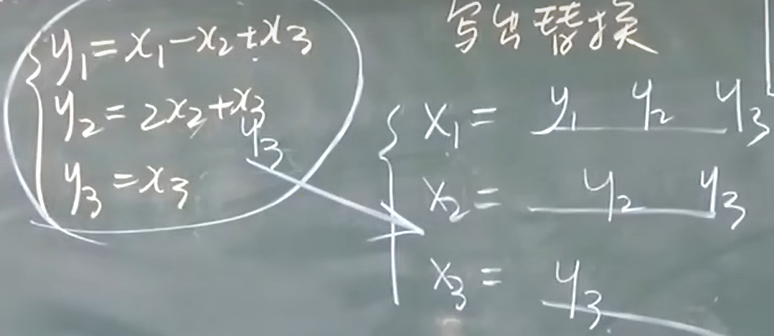
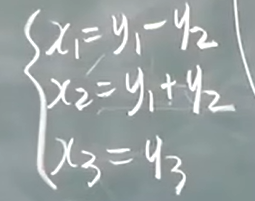
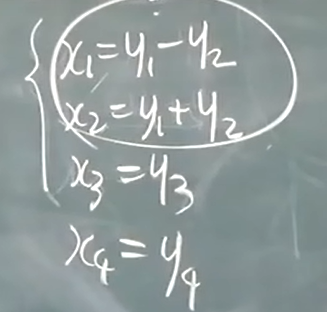

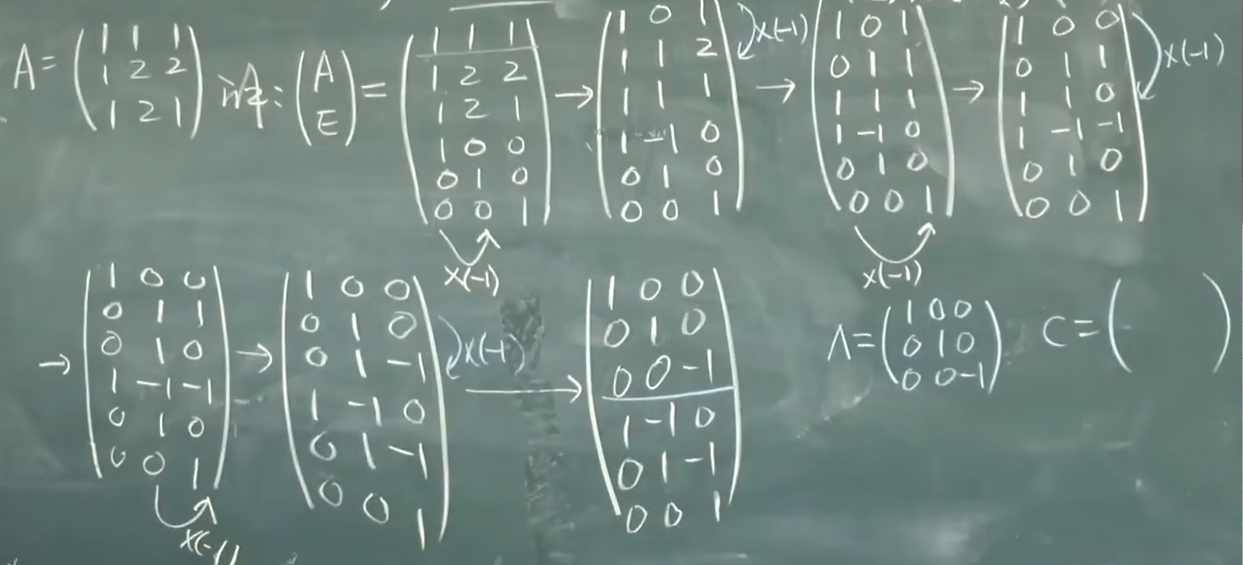
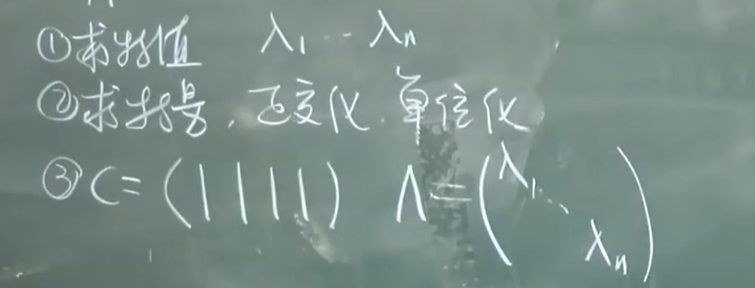
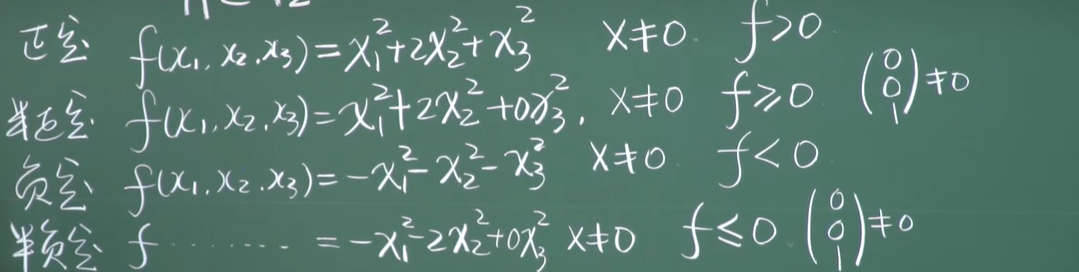
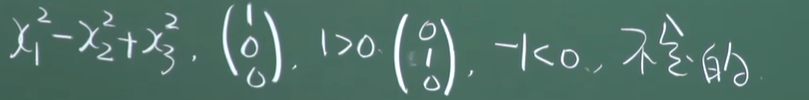
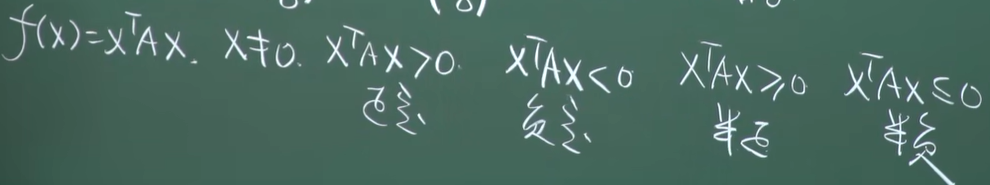
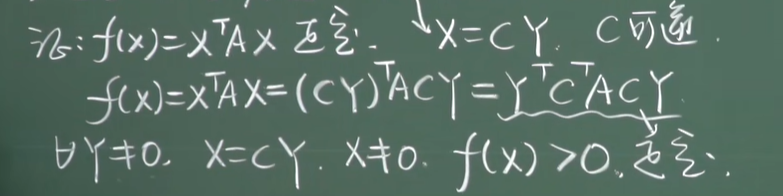

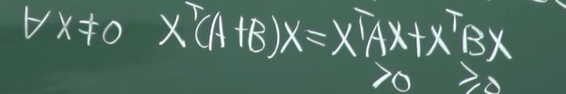

 浙公网安备 33010602011771号
浙公网安备 33010602011771号