树

结点的度：结点拥有的孩子数
树的度：树中所有结点度的最大值
树的深度：树中结点的最大层次

 

二叉树

二叉树与树的最主要区别：二叉树一定要区分左子树和右子树，而树在只有一个孩子的情况下无需区分

 

二叉树的性质

• 在二叉树的第i层上至多有2^i-1个结点，至少有1个结点（i>=1）
• 深度为k的二叉树至多有2^k-1个结点（k>=1)
• 对任何一棵二叉树T，如果叶子数为n₀，度为2的结点数为n₁，则n₀=n₁+1
• 若双亲结点是i，则左孩子结点为2i，右孩子结点为2i+1

 

b：总边数

n：总结点数

n₀ ：度为0的结点数

n₁：度为1的结点数

n₂：度为2的结点数

b=n-1

b=2n₂+n₁

 

二叉树的遍历

先序遍历：根结点、左子树、右子树
中序遍历：左子树、根结点、右子树
后序遍历：左子树、右子树、根节点

二叉树遍历的递归算法转为非递归算法关键：用栈存储回溯点

二叉树的层次遍历：使用队列。将根结点入队，当队列不空时循环：从队列中出队一个结点，若它有左孩子，将左孩子入队；若它有右孩子，将右孩子入队

 

树的遍历方式

先根遍历
后根遍历
层次遍历

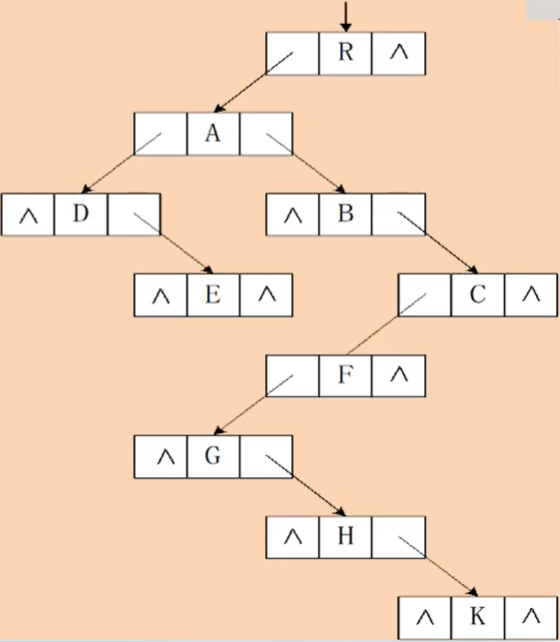
线索二叉树

线索二叉树：利用二叉链表中的空指针域实现。如果某个结点的左孩子为空，则将空的左孩子指针域改为指向其前驱；如果某结点的右孩子为空，则将空的右孩子指针域改为指向其后继
对二叉树按某种遍历次序使其变为线索二叉树的过程叫线索化

为了区分lchild和rchild指针到底是指向孩子的指针，还是指向前驱或后继的指针，对二叉链表中每个结点增设两个标志域ltag和rtag，并约定：
ltag=0表示lchild指向该结点的左孩子
ltag=1表示lchild指向该结点的前驱
rtag=0表示rchild指向该结点的右孩子
rtag=1表示rchild指向该结点的后继

顺序存储

二叉树的顺序存储：按满二叉树的结点层次编号，依次存放二叉树中的数据元素
结点间关系蕴含在其存储位置中，适于存储满二叉树和完全二叉树

 

孩子兄弟表示法

孩子兄弟表示法：用二叉链表作为树的存储结构，链表中每个结点的左指针域指向第一个孩子结点，右指针域指向下一个兄弟结点

 

 

 

 

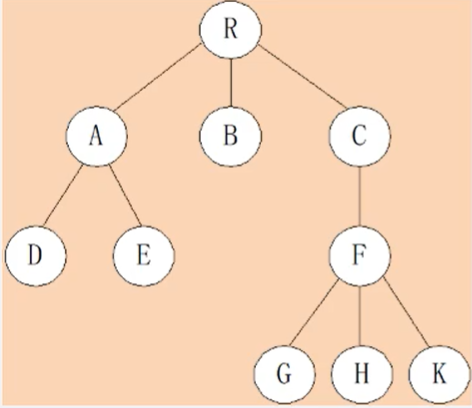
树与二叉树的转换

将树通过孩子兄弟表示法转换为二叉树

二叉链表

在n个结点的二叉链表中，有n+1个空指针域

 

 

 

三叉链表

 

 

 

满二叉树

定义：一棵深度为k且有2^k-1个结点的二叉树称为满二叉树

叶子结点全部在最底层

 

完全二叉树

定义：在满二叉树中，从最后一个结点开始连续去掉n个结点（n>=0），即是一棵完全二叉树（注意：一定是连续去掉）

叶子结点只分布在层次最大的两层上

满二叉树一定是完全二叉树

 

哈夫曼树（最优二叉树）