剑指 Offer 14- I. 剪绳子

可以说是做的第一道比较有难度的动态规划题

 

 思路：

感觉是dp[n]肯定是和dp[n-1]等等有什么关系

但是没想到还挺复杂的

dp[n]可以分为第一次剪出来的和剩下的

这样就是1，dp[n-1] ;2,dp[n-2]，一直到n-1,dp[1]

但是问题在于这个至少剪成2段的条件

这样剩下的既有可能是dp[n-1]，也有可能就是n-1

举个例子，n=3，当第一次剪下1时，剩下既可以是dp[2]，也可以是2

显然2>dp[2]

这样我们列出递推方程

 

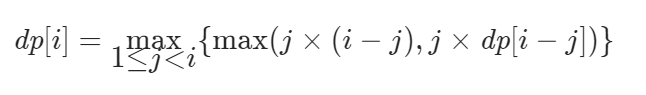
 j代表第一次剪下的长度

一个小疑问是总感觉这样会出现某种重复

 

第二个问题就是如何计算这个dp[n]了

由于是动态规划，当计算dp[n]时我们要从dp[2]算到dp[n-1]，这是第一重循环

又由于每次计算都需要计算j从1到i-1这么多种情况，这是第二重循环

于是代码如下：

class Solution {
    public int cuttingRope(int n) {
        int[] dp=new int[n+1];//dp[0]到dp[n]吗？
        // dp[2]=1;
        for(int i=2;i<n+1;i++)//从dp[2]一直计算到dp[n]
        {
            int curMax=0;
            for(int j=1;j<i;j++)//第一次取从1取到i-1
            {
                curMax=Math.max(curMax,Math.max(j*(i-j),j*dp[i-j]));
            }
            dp[i]=curMax;
        }
        return dp[n];
}}

这个curMax只是一种从j的各种情况中取最大的方式

 

问题：

什么时候用动态规划，什么时候用递归呢

二叉树的时候用过好多次递归，那些情况

 

感觉动态规划还是蛮难的