回文子列 -- 连续与不连续
题目:
- 647 回文子串 https://leetcode.cn/problems/palindromic-substrings/description/
讲解: https://programmercarl.com/0647.%E5%9B%9E%E6%96%87%E5%AD%90%E4%B8%B2.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE - 5 最长回文子串 https://leetcode.cn/problems/longest-palindromic-substring/description/
- 516 最长回文子序列 https://leetcode.cn/problems/longest-palindromic-subsequence/description/
1. 统计回文子串的数目
题目:给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
思路:
- 使用动态规划来解决,定义二维数组
dp表示从i到j的子串是否为回文子串。 - 初始化所有长度为 1 的子串都是回文子串,即
dp[i][i] = true。 - 状态转移方程:
dp[i][j] = s[i] == s[j] && dp[i+1][j-1],即当前子串是否为回文取决于首尾字符是否相等且去掉首尾后的子串是否为回文。 - 统计回文子串的数量,如果
dp[i][j]为 true,则回文子串数量加一。
代码:
class Solution:
def countSubstrings(self, s: str) -> int:
#https://programmercarl.com/0647.%E5%9B%9E%E6%96%87%E5%AD%90%E4%B8%B2.html#%E6%80%9D%E8%B7%AF
# dp[i] 和 dp[i-1] ,dp[i + 1] 关系不明显
# 所有用布尔类型的dp[i][j]:表示区间范围[i,j]
#(注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
#当然也可以从初始化为0 : https://leetcode.cn/problems/longest-palindromic-subsequence/solutions/2203001/shi-pin-jiao-ni-yi-bu-bu-si-kao-dong-tai-kgkg/
dp = [[False]*(len(s))for _ in range(len(s))]
res = 0
# 当s[i]与s[j]不相等,dp[i][j]一定是false。
# 当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
# 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
# 情况二:下标i 与 j相差为1,例如aa,也是回文子串
# 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
#dp[i][j]由dp[i+1][j-1]、dp[i+1][j]、dp[i][j-1]转移而来故 i需倒序(即先算出[i+1])j正序
for i in range(len(s)-1,-1,-1):
for j in range(i,len(s)):
# 判断是否是回文子串
if s[i] == s[j] and (j - i <= 1 or dp[i + 1][j - 1]):
dp[i][j] = True
res += 1
return res
#双指针法
# class Solution:
# def countSubstrings(self, s: str) -> int:
# result = 0
# for i in range(len(s)):
# result += self.extend(s, i, i, len(s)) #以i为中心
# result += self.extend(s, i, i+1, len(s)) #以i和i+1为中心
# return result
# def extend(self, s, i, j, n):
# res = 0
# while i >= 0 and j < n and s[i] == s[j]:
# i -= 1
# j += 1
# res += 1
# return res
2. 找到最长回文子串
题目:给你一个字符串 s,找到 s 中最长的回文子串。
思路:
- 使用动态规划来解决,定义二维数组
dp表示从i到j的子串是否为回文子串。 - 初始化所有长度为 1 的子串都是回文子串,即
dp[i][i] = true。 - 状态转移方程:
dp[i][j] = s[i] == s[j] && dp[i+1][j-1],即当前子串是否为回文取决于首尾字符是否相等且去掉首尾后的子串是否为回文。 - 在状态转移的过程中,记录最长的回文子串的起始位置和长度。
代码:
def longestPalindrome(s):
n = len(s)
# 创建二维数组 dp,表示从索引 i 到索引 j 的最长回文子串的长度
dp = [[0] * n for _ in range(n)]
# 记录最长回文子串的起始位置和长度
start, max_len = 0, 1
# 外层循环从字符串末尾开始遍历
for i in range(n - 1, -1, -1):
# 初始化长度为 1 的子串为回文串
dp[i][i] = 1
# 内层循环从 i+1 开始,遍历右侧的字符
for j in range(i + 1, n):
# 判断索引 i 和 j 处的字符是否相等
if s[i] == s[j]:
# 如果相邻或者去掉首尾后的子串是回文的,更新 dp[i][j]
if j - i == 1 or dp[i + 1][j - 1] > 0:
dp[i][j] = j - i + 1
# 更新最长回文子串的起始位置和长度
if dp[i][j] > max_len:
start = i
max_len = dp[i][j]
# 返回最长回文子串
return s[start:start + max_len]
3. 找到最长回文子序列
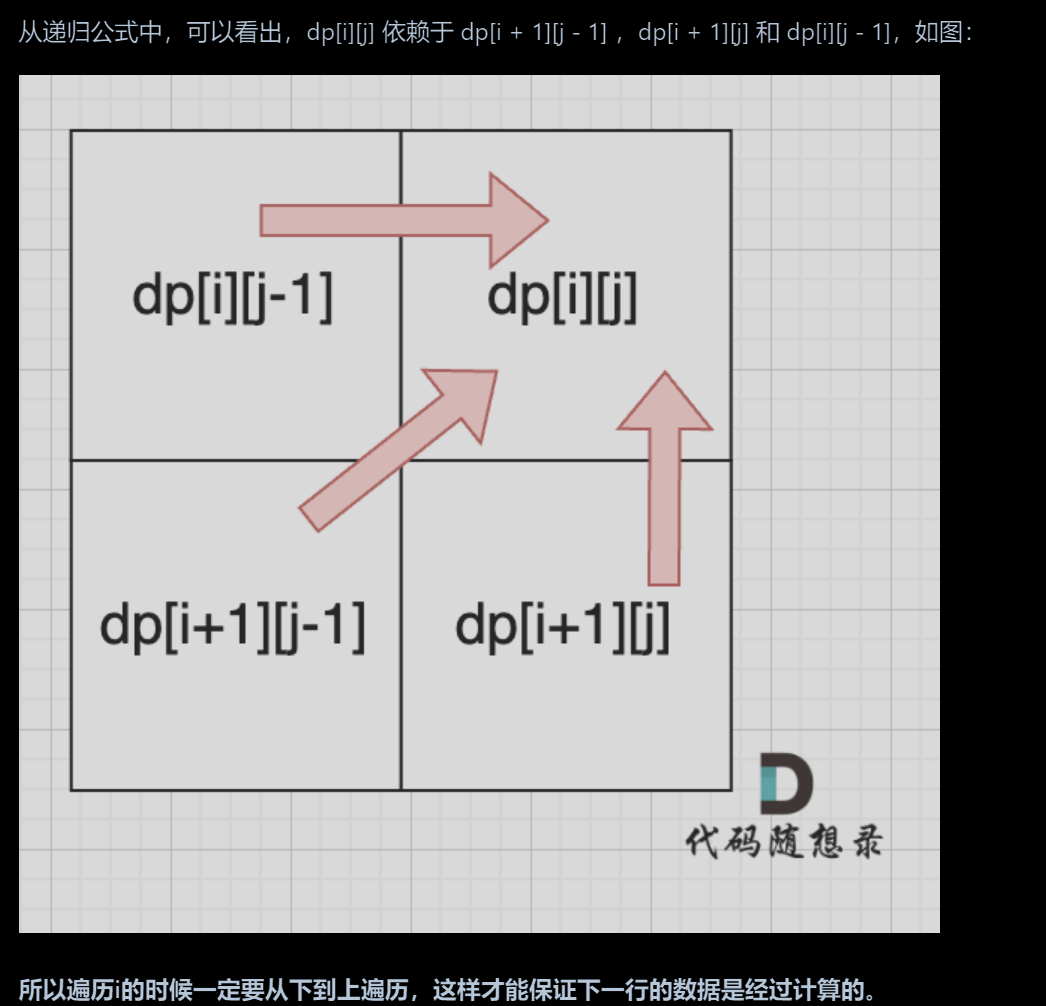
注:图片截取自“代码随想录”
思路:
- 使用动态规划来解决,定义二维数组
dp表示从i到j的子序列的最长回文长度。 - 初始化所有长度为 1 的子序列的最长回文长度为 1。
- 状态转移方程:
dp[i][j] = dp[i+1][j-1] + 2,即当前子序列的最长回文长度取决于首尾字符是否相等且去掉首尾后的子序列的最长回文长度加 2。 - 优化 改用一维dp 需加入临时变量记录过程值
- 在状态转移的过程中,记录最长的回文子序列的长度。
代码:
def longestPalindromeSubseq(s):
n = len(s)
#dp[i][j] 表示从索引 i 到索引 j 的最长回文子序列的长度。
dp = [[0] * n for _ in range(n)]
# 外层循环从字符串末尾开始遍历
for i in range(n - 1, -1, -1):
dp[i][i] = 1 #i=j即长度为一,初始化长度为 1 的子串为回文串
# 内层循环从 i+1 开始,遍历右侧的字符
for j in range(i + 1, n):
#也可改成三次判断取代max/min 减少时间复杂度!!!
if s[i] == s[j]:
# 如果相等,最长回文子序列的长度为前一个状态加上 2
dp[i][j] = dp[i + 1][j - 1] + 2
else:
# 如果不相等,最长回文子序列的长度为左侧或上方的最大值
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
return dp[0][n - 1]
一维dp
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
#一维dp
n = len(s)
# 创建一维动态规划数组 dp,表示以当前索引 i 结尾的最长回文子序列的长度
dp = [0] * n
for i in range(n - 1, -1, -1):
# 初始化当前位置 i 的最长回文子序列长度为 1
dp[i] = 1
# 用于保存 dp[i+1][j],即上一行同一列的值
pre = 0
for j in range(i + 1, n):
# 保存当前 dp[j],即当前行上一列的值
tmp = dp[j]
dp[j] = pre + 2 if s[i] == s[j] else max(dp[j], dp[j - 1])
# 更新 prev,为下一轮迭代保存 dp[i+1][j]
pre = tmp
return dp[-1]
在这三个问题中,主要区别在于动态规划数组的定义和状态转移方程的不同。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号