【Tai_mount】 算法学习 - 数据结构 - 线段树

https://www.luogu.com.cn/problem/P3372

问题背景：

对于一个长度为n的序列，将要进行维护，本问题中有两种操作：

• 查询：对序列中l-r区间内的数求和
• 修改：对l-r区间内所有数都加k

以下先举两种数据结构：

• 直接存储在长度为n的一维数组a[n]中，查询即循环求a[l]至a[r]之和
• 储存s[n]=为从第1到第n个数的和 前缀和

对于两种操作的时间复杂度：

• 直接存数
  • 查询：O(n)
  • 修改：O(n)
• 前缀和
  • 查询：O(1)
  • 修改：O(n)

那么，就需要一种更快捷的方式了！

线段树

原理：

将这个序列二分，如：以a1-a8举例

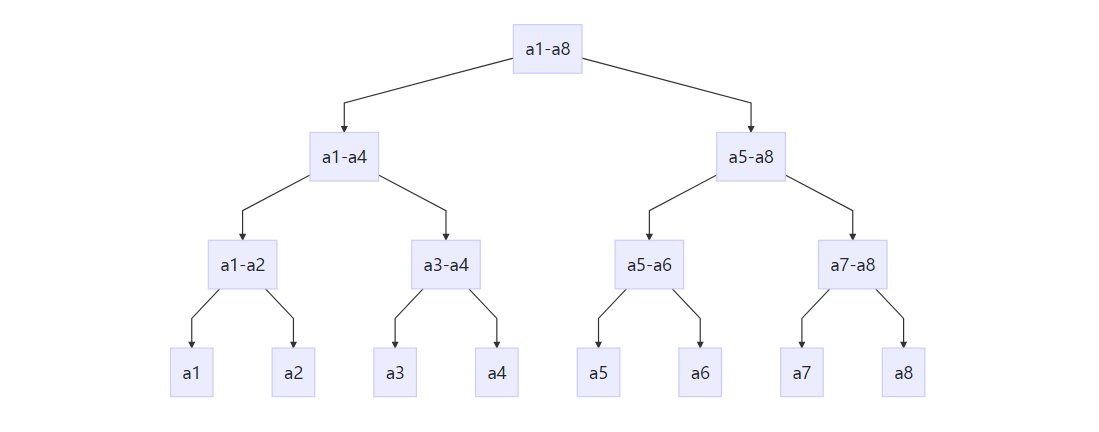
这样就构成了一个二叉树

每个节点都存储了所对应序列之和

这样，无论是查询还是修改，都可以分给两个子函数，递归运算

建树：

每个节点有四个信息（以上图节点5：a3-a4）举例：

• 序列左界 int l=3(c)
• 序列右界 int r=4
• 和 long long sum=a[3]+a[4]
• 未向下传递的修改 long long tag=0

tag这个信息下面再说
其他的四个信息应该都没有问题，建个结构体就行

struct node{
	int l;
	int r;
	long long sum;
	long long tag; 
}; 

在这里定义的结构体数组名字是seg node seg[N<<2];

注意此处一定要定义4倍的N,长度为n的序列最多会有4倍的节点数量

2的n次方会有2的n+1次方的节点个数

2的n+1次方会有n+2次方的节点个数

2的n+1次方和2的n次方之间的数，必须取到4倍

---

建树方法一：

直接利用“修改”的函数，时间复杂度为O(nlogn)

---

建树方法二：

程序前的定义：

#define ls (rt<<1)
#define rs (ls|1)
#define mid ((l+r)>>1)

rt为父节点的编号
rs为右边子节点的编号
ls为左边子节点的编号
mid为中间的分割点

---

void build(int rt,int l,int r){
	seg[rt].l=l; seg[rt].r=r; seg[rt].tag=0;//赋值l,r,tag（tage初值为0）
	if(l==r) {seg[rt].sum=a[l]; return;}//如果是叶节点就直接赋值数组里的数
	build(ls,l,mid); build(rs,mid+1,r);//递归
	seg[rt].sum=seg[ls].sum+seg[rs].sum;//已递归完毕直接求sum值
	return;
}

build(rt,l,r) 意味：创建一个编号为rt，包含了al-ar之和的子节点

建树方法为：首先创建一个父节点，其编号为1，l为整个序列的左界,r为整个序列的右界

而父节点的sum值运用递归，相加其两个子节点获得

直到叶节点的sum值就直接获取数列中这个数

子节点的左右界都可以由父节点求得，详见程序前的定义部分

查询：

先上程序：

long long query(int rt,int l,int r){
	if(seg[rt].r<l||seg[rt].l>r) return 0;//当节点所在区间与所求区间没有交集，直接返回0
	if(seg[rt].r<=r&&seg[rt].l>=l) return seg[rt].sum;//当节点所在区间被所求区间包含，返回这个节点的sum值
	pushdown(rt);//把“tag”的修改值下降到子节点
	return query(ls,l,r)+query(rs,l,r); //上两种条件都不满足，即该节点与所求区间有交集，但不被包含，分成左右子节点两部分递归
}

分三种情况，都已经写在程序里了
查询在rt子节点中的属于l-r（被查询区间的）sum值

修改：

程序：

void update(int rt,int l,int r,long long change){
	if(seg[rt].r<l||seg[rt].l>r) return;//如果没有交集，直接过
	if(seg[rt].r<=r&&seg[rt].l>=l){
		seg[rt].tag+=change;//未被传下去的tag
		seg[rt].sum+=(seg[rt].r-seg[rt].l+1)*change;//总和加上区间内数的数量乘k
		return;
	}
	pushdown(rt);//把tag传下去
	update(ls,l,r,change); update(rs,l,r,change);//递归传给子节点去更新
	seg[rt].sum=seg[rs].sum+seg[ls].sum; //更新过子节点后自己也要更新
	return;
}

对rt区间与l-r区间内数+k

修改的实现与查询有许多不同

如果这一整段都在被修改的区间中，不会对这个节点的子节点同时修改，而是会拦截下来，记入到tag中，每次访问到这个节点，包括加上tag的这一次，再往下传递一层。这样可以省去不必要的传递。

对于传递这一点，会有另外的 pushdown函数

void pushdown(int rt){
	seg[ls].tag+=seg[rt].tag; //左子节点加上tag
	seg[rs].tag+=seg[rt].tag; //右子节点加上tag
	seg[ls].sum+=(seg[ls].r-seg[ls].l+1)*seg[rt].tag; //左子节点sum加上
	seg[rs].sum+=(seg[rs].r-seg[rs].l+1)*seg[rt].tag; //右子节点sum加上
	seg[rt].tag=0;	//把 tag清零
	return;
}

pushdown函数要定义在query和update之前，因为其在后两个函数中有调用