博客作业06--图
一、学习总结(2分)
1. 图的思维导图
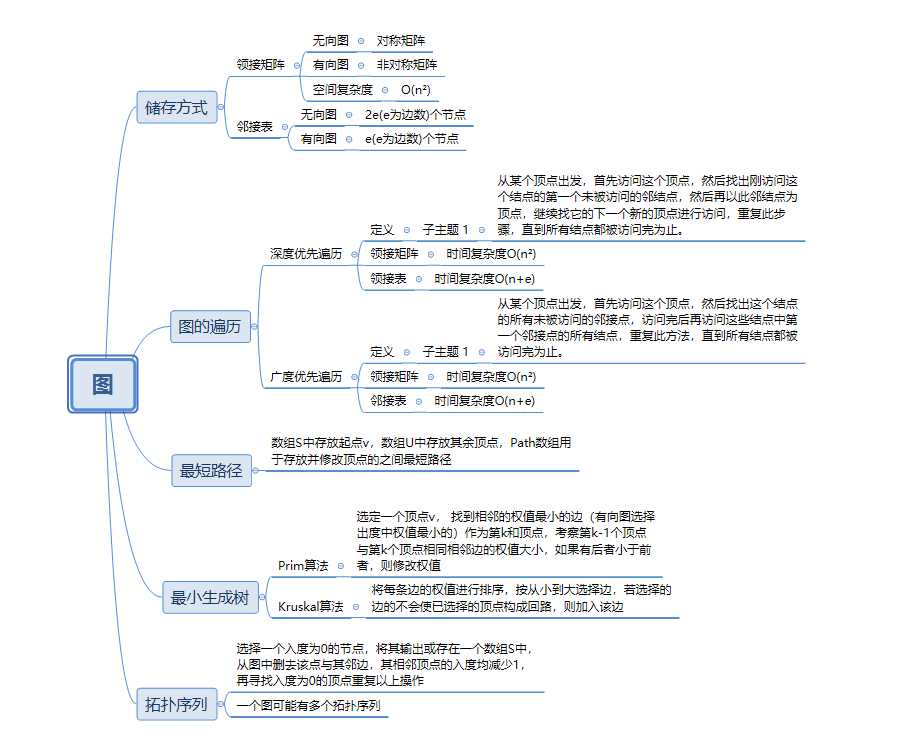
2. 图结构学习体会
深度遍历算法
深度优先遍历从某个顶点出发,首先访问这个顶点,然后找出刚访问这个结点的第一个未被访问的邻结点,然后再以此邻结点为顶点,继续找它的下一个新的顶点进行访问,重复此步骤,直到所有结点都被访问完为止。
广度遍历算法
广度优先遍历从某个顶点出发,首先访问这个顶点,然后找出这个结点的所有未被访问的邻接点,访问完后再访问这些结点中第一个邻接点的所有结点,重复此方法,直到所有结点都被访问完为止。
Prim算法
首先以一个结点作为最小生成树的初始结点,然后以迭代的方式找出最小生成树中各结点权重最小的边,并加到最小生成树中。(加入之后如果产生回路了就要跳过这条边,选择下一个结点。)当所有的结点都加入到最小生成树中后,就找出了这个连通图的最小生成树。和Kruscal算法
Dijkstra算法
Kruskal算法在找最小生成树结点之前,需要对权重从小到大进行排序。将排序好的权重边依次加入到最小生成树中,(如果加入时产生回路就跳过这条边,加入下一条边)。当所有的结点都加入到最小生成树中后,就找到了这个连通图的最小生成树。
拓扑排序算法
拓扑排序对应施工的流程图具有特别重要的作用,它可以决定哪些子工程必须要先执行,哪些子工程要在某些工程执行后才可以执行。为了形象地反映出整个工程中各个子工程(活动)之间的先后关系,可用一个有向图来表示,图中的顶点代表活动(子工程),图中的有向边代表活动的先后关系,即有向边的起点的活动是终点活动的前序活动,只有当起点活动完成之后,其终点活动才能进行。通常,我们把这种顶点表示活动、边表示活动间先后关系的有向图称做顶点活动网(Activity On Vertex network),简称AOV网。
一个AOV网应该是一个有向无环图,即不应该带有回路,因为若带有回路,则回路上的所有活动都无法进行(对于数据流来说就是死循环)。在AOV网中,若不存在回路,则所有活动可排列成一个线性序列,使得每个活动的所有前驱活动都排在该活动的前面,我们把此序列叫做拓扑序列(Topological order),由AOV网构造拓扑序列的过程叫做拓扑排序(Topological sort)。AOV网的拓扑序列不是唯一的,满足上述定义的任一线性序列都称作它的拓扑序列。
二、PTA实验作业(4分)
题目1:图着色问题
1. 设计思路(伪代码或流程图)
主函数
输入顶点数V,边数E,颜色数K
for i=0 to E-1
输入E条边并添加至容器尾部
输入需检查信息条数N
while(N - -)
初始化visited数组为0
for i=1 to V
输入V个顶点的颜色
记录所有顶点所用的颜色数
if(着色的颜色数!=题目所给的颜色数) 输出No
else
flag = Check(); //调用Check函数
if(flag不等于0) 输出Yes
else 输出No
end while
Check函数 //检查着色
for i=1 to V
for j=0 to g[i].size-1
if(两相邻顶点颜色相同)
返回0
end j
end i
返回1
2. 代码截图


3. PTA提交列表说明。
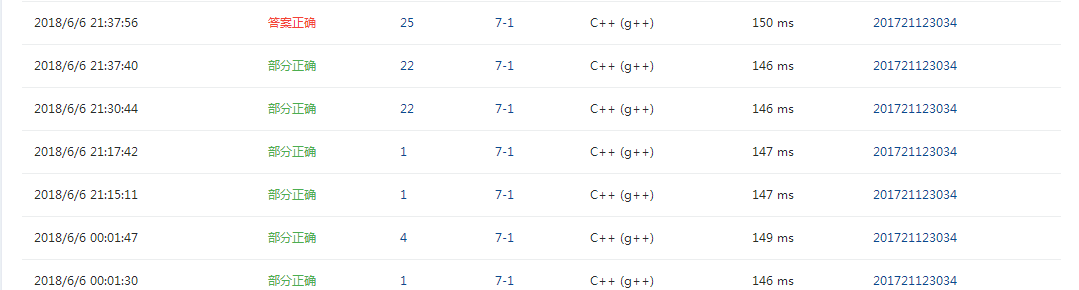
- 做的时候一直认为颜色数只有>=K才是错的,然后改成 ! = 才正确
- 没有在每一次大循环的时候将visited数组初始化为0
题目2:六度空间
1. 设计思路(伪代码或流程图)
int BFS(int x)函数
访问x
cnt=1
层数level=0
令这一层访问的最后一个节点last = x
x入队列
while(队列不为空)
出队一个元素
for i=1 to N-1
if(g[pop][i]不为空并且i未被访问过)
i入队
这个节点人数+1
尾元素tail = i
if(这一层遍历完)
层数level+1
将尾元素tail赋给最后一个节点last
if(层数为6) 结束循环
end while
返回节点人数cnt
主函数
输入人数N,和关系数M
for j=1 to M
输入每条关系的两个人
令矩阵g[u][v]=g[v][u]=1
for i=1 to N
初始化visited数组为0
count = BFS(i); //调用BFS函数
输出计算出的百分比
return 0;
2. 代码截图

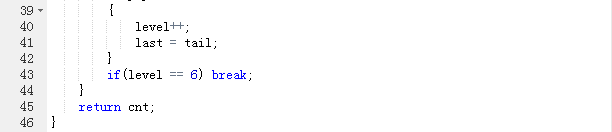

3. PTA提交列表说明。
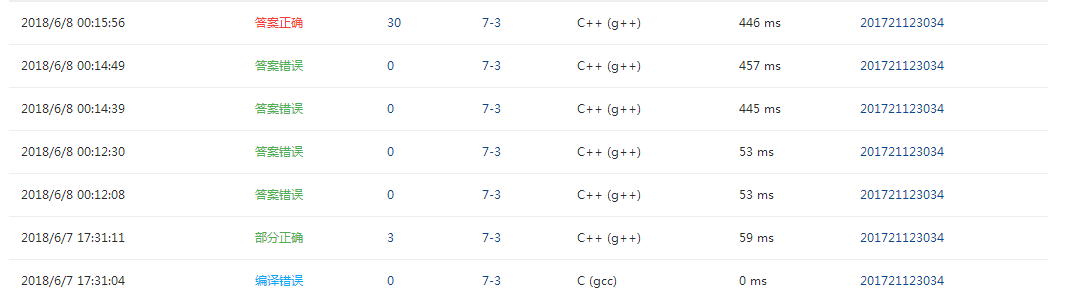
- 循环下标出错
没有初始化visited数组

题目3:公路村村通
1. 设计思路(伪代码或流程图)
Prim函数
sum=0;
访问第一个元素
for i=1 to n
将lowcost的初值都附为与顶点1所连接的边的权值
for i=1 to n-1
min初始化为INF记录最小权值,p=-1记录与最小权值有关的点的下标
for j=1 to n
if(lowcost[j]小于原来最小权值min,并且未被访问过)
min改为lowcost[j]
最小邻边下标p改为j
if(i与其他顶点无通路)
返回 -1
总成本加上最小权值边min
访问p
for i=1 to n
if 这个点的权值lowcost[j]小于原来最小权值,并且未被访问过
将该点最小权值改为lowcost[j]
end for
return 总成本sum
2. 代码截图



3. PTA提交列表说明。
- MAXV 0x3f3f 这里,如果是0x3f3f3f虽然答案正确但是会一直循环这个找最小值的操作
- 最开始不是这个做法,这个做法是去百度了解到的,原先的做法是先建立顶点与顶点之间的朋友关系,再判断是否超过6,但是答案错误,可能是朋友关系没建立成功,还会再研究一下。
三、截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
1. PTA排名

2. 我的总分:200(得2分)
四、 阅读代码(必做,1分)
n皇后问题
经典的n皇后问题,在一个n*n的棋盘上放置n个皇后,使得不能互相攻击到,皇后的攻击范围的同一行,同一列以及同一个斜线。要求输出所有不会互相攻击到的摆放方式的总数目,以及每种摆放方式。所有通过旋转,对称都方式得到的摆放方式均认为是不同的摆放方式。棋盘被编号为0到n-1行,为0到n-1列。


巧妙地在深搜时调用check函数检验第r行第c列是否可以放皇后,从而解决n皇后问题,做法简单易懂。时间复杂度O(n²)。
参考网址:
https://blog.csdn.net/jal517486222/article/details/80040249
五、提交截图





 浙公网安备 33010602011771号
浙公网安备 33010602011771号
