哈尔滨工业大学计算机学院-最优化方法-课程总结

1. 前言

• 本课程由数学系开设，旨在讲述求解数学问题的各种最优化方法。
• 本博客仅对课程中的如下内容进行详细介绍：
  • 凸集、凸函数、凸规划
  • 线性规划
    • 线性规划标准形式
    • 单纯形法
  • 无约束最优化方法
    • 最优性条件
    • 最速下降法
    • 牛顿法
  • 约束最优化方法
    • Kuhn-Tucker 条件
    • 罚函数法
    • 闸函数法

2. 凸集、凸函数、凸规划

2.1 凸集

• 凸集的定义：
  • 设\(S \subseteq \mathbf { R } ^ { n }\)，若\(\forall x ^ { ( 1 ) } , x ^ { ( 2 ) } \in S , \lambda \in [ 0,1 ]\)，必有\(\lambda x ^ { ( 1 ) } + ( 1 - \lambda ) x ^ { ( 2 ) } \in S\)，则称\(S\)为凸集。
• 形式化理解凸集的定义，即集合中任意两点连线上的点都在集合内。
• 对于凸集的证明，往往利用定义进行证明。

2.2 凸函数

• 凸函数的定义：
  • 设集合\(S \subseteq \mathbf { R } ^ { n }\)为凸集，函数\(f : S \rightarrow \mathbf { R }\)。若\(\forall x ^ { ( 1 ) } , x ^ { ( 2 ) } \in S , \lambda \in ( 0,1 )\)，恒有\(f \left( x ^ { ( 1 ) } + ( 1 - \lambda ) x ^ { ( 2 ) } \right) \leq \lambda f \left( x ^ { ( 1 ) } \right) + ( 1 - \lambda ) f \left( x ^ { ( 2 ) } \right)\)，则称\(f\)为凸集\(S\)上的凸函数。
  • 如果上面不等式以严格不等式成立，则称\(f(x)\)为凸集\(S\)上的严格凸函数。
• 凸函数的证明：
  • 凸函数与一阶特征、二阶特征互为充要条件，往往利用二阶特征进行证明，
  • 二阶特征：
    • \(f\)在\(S\)上凸，等价于，\(S\)中任意一点，其对应的海塞矩阵半正定。
    • \(f\)在\(S\)上严格凸，等价于，\(S\)中任意一点，其对应的海塞矩阵正定。
• 凸函数是定义在凸集上的函数，如果要证明凸函数，首先要说明定义域为凸集。

2.3 凸规划

• 凸规划的定义：
  • 如果问题\((fS)\)中，\(S\)为凸集，\(f\)为凸函数，则称这个问题是凸规划。
• 凸规划的定理：
  • 在凸规划问题中，局部最优解也是全局最优解。
  • 如果\(f\)为严格凸函数，则该局部最优解是唯一全局最优解。
• 依据凸规划的定理，证明一个局部最优点为唯一全局最优解，只需证明函数\(f\)为严格凸函数。
• 凸规划的性质十分利于我们寻找问题的最优解，因此我们经常需要证明一个问题是凸规划问题。

3. 线性规划

3.1 线性规划标准形式

• 首先介绍线性规划的标准形式，之后的单纯形法都是在标准形式上进行计算，对于不是标准形式的线性规划需要对其进行转换。
• 标准形式如下：

\[( L P )\left\{ \begin{array} { c } { \operatorname { max } z=c ^ { T } x } \\ {s.t. \quad Ax = b } \\ {\quad \quad x \geq 0 } \end{array} \right. \]

• 四个特点：
  • 目标最大化
  • 约束为等式
  • 决策变量非负
  • 右端项非负
• 采用如下方式，将一般形式转化为标准化形式：
  • 极小化目标函数的问题：利用负号转化为目标最大化
  • 约束不是等式的问题：引入松弛变量
  • 变量无符号限制的问题：用两个非负变量之差来表示一个无符号限制的变量
  • 右端项有负值的问题：乘以\(-1\)

3.2 单纯形法

• 单纯形法的基本思路是有选择地取基本可行解，即是从可行域的一个极点出发，沿着可行域的边界移到另一个相邻的极点，要求新极点的目标函数值不比原目标函数值差。
• 单纯形法要求系数矩阵中存在单位阵，将其作为初始的基本可行解，之后一步步迭代。对于某些标准形式中不含有单位阵的线性规划问题，可以采用大M法和两阶段法。
• 单纯形法的计算比较简单，这里只给出例子进行说明。

\[( L P ) \quad \left\{ \begin{array} { c } { \operatorname { max } z=1500x_1+2500x_2} \\ { 3x_1+2x_2+x_3 = 65 } \\ { 2x_1+x_2+x_4 = 40 }\\ { 3x_2+x_5 = 75 }\\ { x_1,x_2,x_3,x_4,x_5 \geq 0 } \end{array} \right. \]

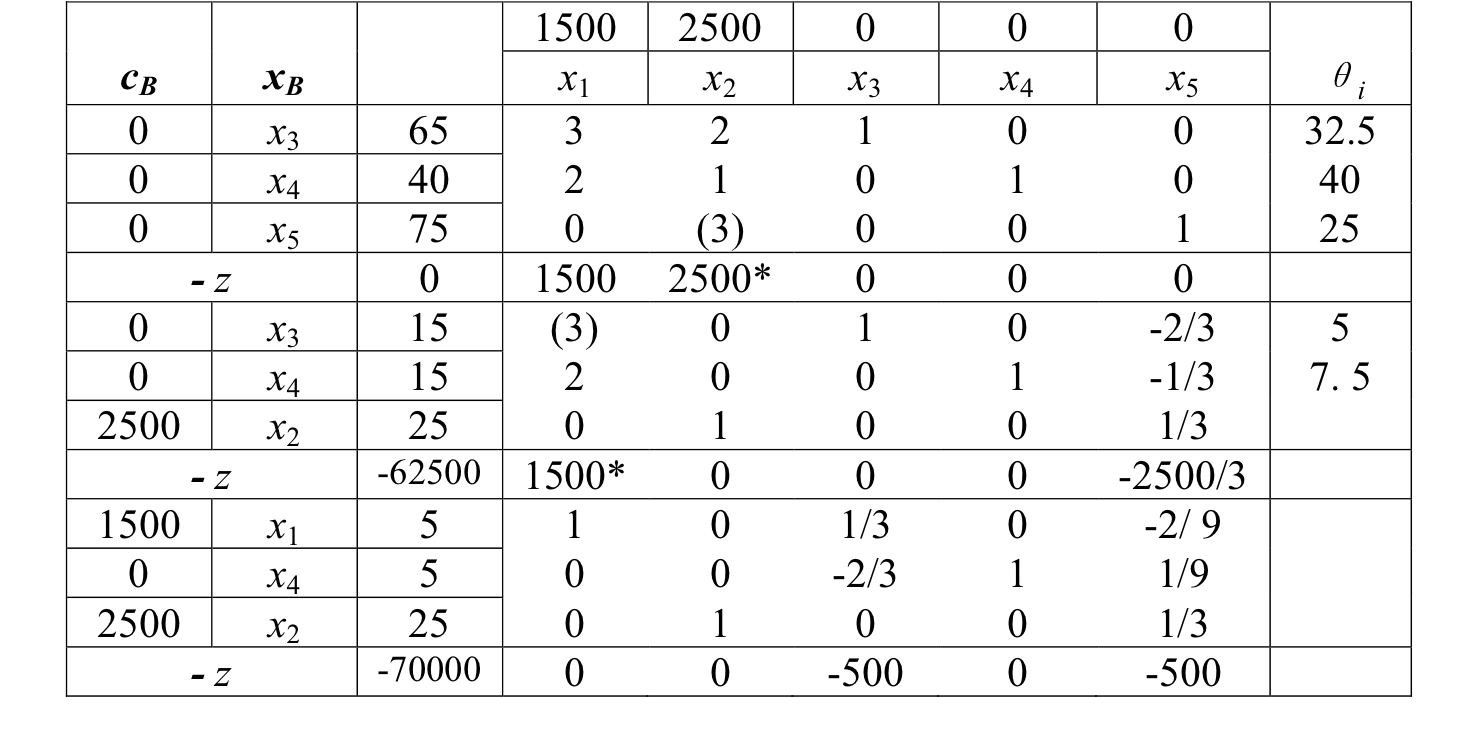
• 单纯形表如下所示：
  
• 最优解为\(x _ { 1 } = 5, x _ { 2 } = 25 , x _ { 4 } = 5\)。
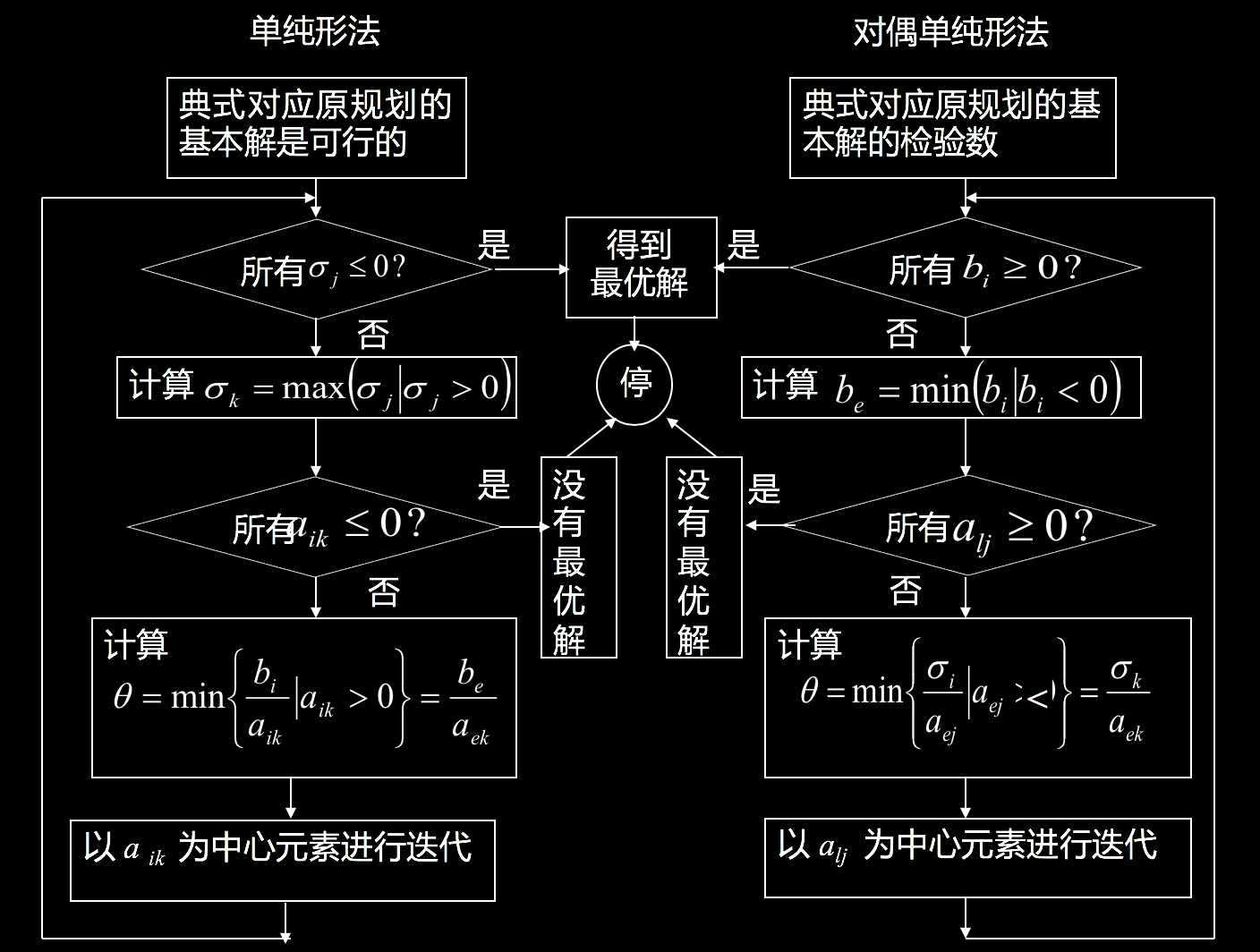
• 与单纯形法相对应的还有对偶单纯形法，二者的算法流程图对比如下所示：
  

4. 无约束最优化方法

4.1 最优性条件

• 一阶必要条件：如果\(x^*\)为局部最小点， 则\(x^*\)为驻点，即该点梯度为\(0\)。
• 二阶必要条件：如果\(x^*\)为局部最小点， 则该点梯度为\(0\)，且海塞矩阵半正定。

4.2 最速下降法

• 该方法就是就是梯度下降法的雏形，是求解无约束问题\(minf(x)\)的古老而基本的方法。
• 在迭代收敛的过程中，每一步令该点的负梯度方向为下降方向。
• 在下降方向确定后，需要找到步长\(\lambda\)，由于是单变量求最优的问题，采用一维搜索的方式即可。
• 最速下降法的“最速”是局部性质，在举例最优点较远处下降的比较快，而距离较近的时候会发生扭摆现象。
• 最速下降法是一种线性收敛的算法，在特定条件下具有全局收敛性。
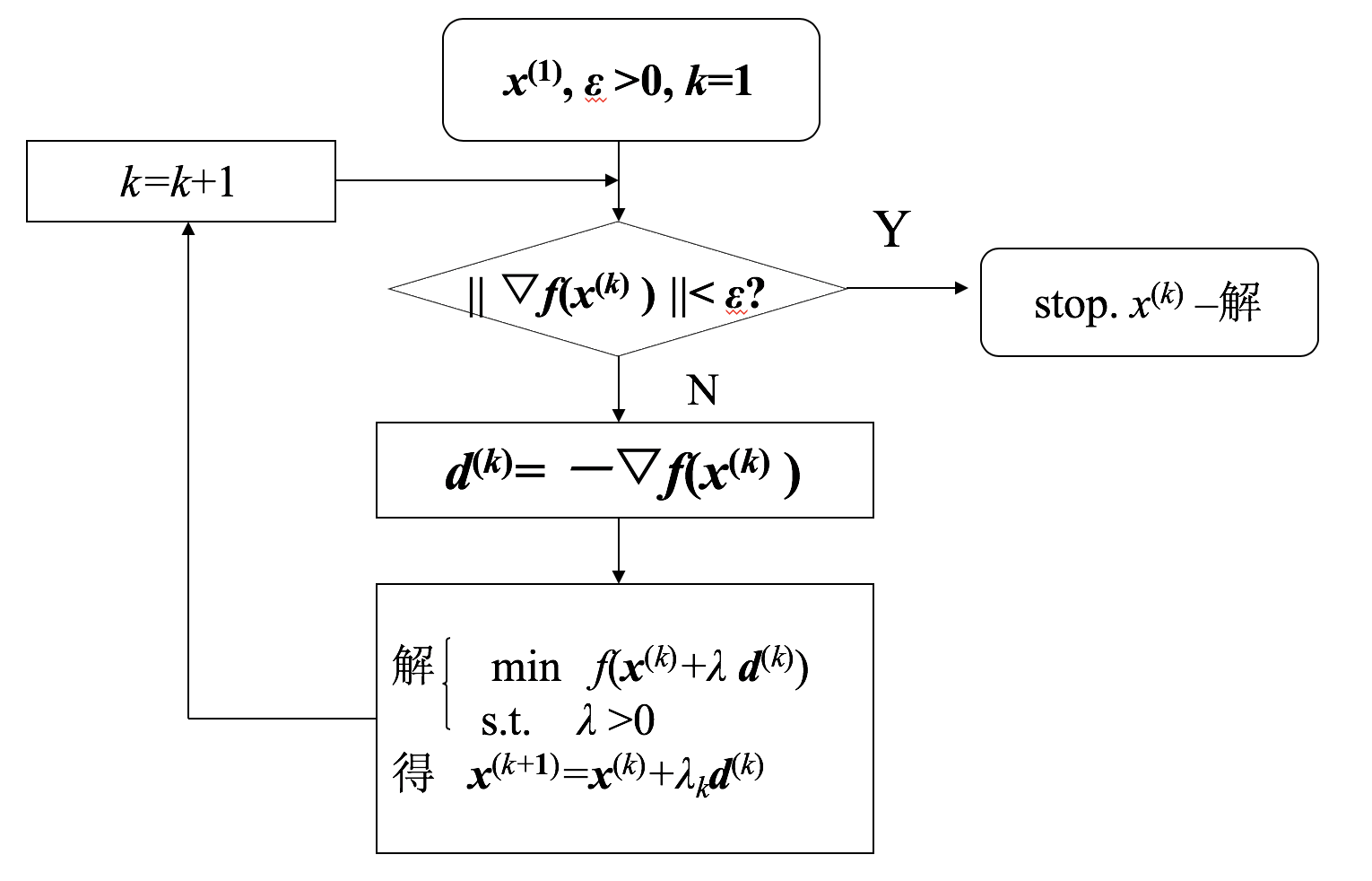
• 该算法的流程图如下所示：
  

4.3 牛顿法

• 牛顿法的思想是利用二次函数近似目标函数，把这个二次函数的极小点作为新的迭代点。该方法应用的前提是函数\(f(x)\)二次连续可微，并且求解的问题是无约束问题\(minf(x)\)。
• 其数学公式由泰勒展开式取前三项得到，即二阶Taylor近似函数：

\[q_k( x ) = f \left( x ^ { ( k ) } \right) + \nabla f ^ { \mathrm { T } } \left( x ^ { ( k ) } \right) \left( x - x ^ { ( k ) } \right) + ( 1 / 2 ) \left( x - x ^ { ( k ) } \right) ^ { \mathrm { T } } \nabla ^ { 2 } f \left( x ^ { ( k ) } \right) \left( x - x ^ { ( k ) } \right) \]

• \(x^{(k)}\)是第\(k\)次的迭代点。
• 对该函数求驻点得到：

\[\nabla q_k( x )= \nabla f \left( x ^ { ( k ) } \right) + \nabla ^ { 2 } f \left( x ^ { ( k ) } \right) \left( x - x ^ { ( k ) } \right) = 0 \]

• 显然只要计算\(x^{(k)}\)点的梯度值，以及海塞矩阵，即可找到下一步的迭代点，相当于最速下降法中的步长为1。将上述公式转换为：

\[\boldsymbol { x } ^ { ( k + 1 ) } = \boldsymbol { x } ^ { ( k ) } - \left[ \nabla ^ { 2 } f \left( \boldsymbol { x } ^ { ( k ) } \right) \right] ^ { - 1 } \nabla f \left( \boldsymbol { x } ^ { ( k ) } \right) \]

• 该公式可以进行计算的前提是海塞矩阵是正定。
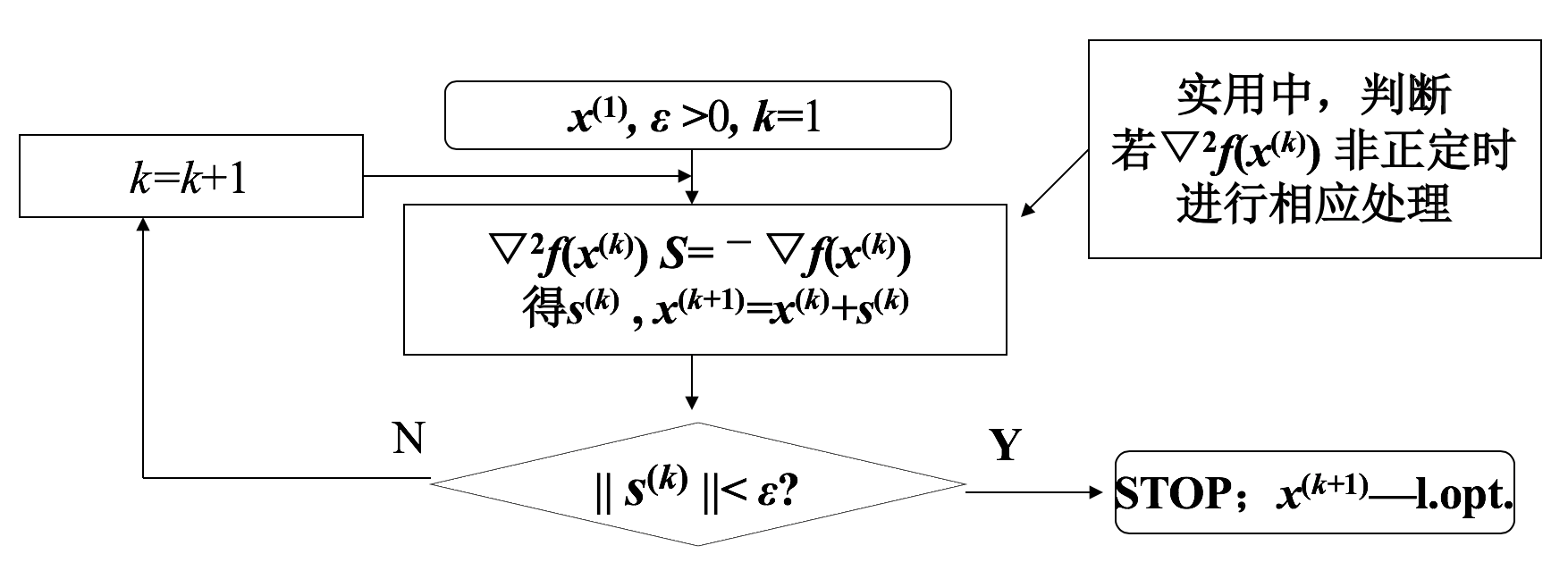
• 牛顿法的算法流程图如下所示：
  
• 牛顿法的优点
  • 牛顿法的收敛速度为二阶，属于平方收敛。牛顿法对正定二次函数一步迭代即可达到最优解，因此具有二次终结性。
• 牛顿法的缺点
  • 牛顿法是局部收敛的，在初始点选择不当时，往往导致不收敛。
  • 牛顿法不是下降算法，当二阶海塞矩阵非正定时，不能保证产生的方向是下降方向。
  • 二阶海塞矩阵必须可逆。
  • 要求函数二阶连续可微，计算量大。

5. 约束最优化方法

• 约束最优化问题是实践中常见的问题，难度大于无约束最优化问题。约束最优化问题的形式一般是\((fgh)\)问题，即：

\[( fgh ) \left\{ \begin{array} { c } { \operatorname { min } f(x)} \\ { s.t. \quad g ( x ) \leq 0 } \\ {\quad \quad h ( x ) = 0 } \end{array} \right. \]

5.1 Kuhn-Tucker条件

• 对于\((fgh)\)问题，K-T条件的公式如下：

\[\nabla f \left( x ^ { * } \right) + \sum _ { i \in I } u _ { i } ^ { * } \nabla g _ { i } \left( x ^ { * } \right) + \sum _ { j = 1 } ^ { l } v _ { j } ^ { * } \nabla h _ { j } \left( x ^ { * } \right) = 0 \]

• 要求所有的\(u\)值非负。

• 通过对上述公式求解，便找到了满足K-T条件的K-T点。

• 在约束最优化问题中，K-T条件相当于无约束最优化问题中的驻点条件，即寻找到K-T点便找到了问题的局部最优解。

  • 有些问题需要说明K-T点是全局最优解，只需要证明问题是凸规划即可，详见2.3章节的介绍。

5.2 罚函数法（外点法）

• 解决玉树问题的一个直接想法是，把违背约束作为对求最小值的一种惩罚，把约束加入到目标函数，从而得到了一个辅助的无约束最优化问题，之后采用无约束最优化方法进行求解，这就是罚函数的基本思想。
  • 在实际求解无约束最优化问题时，求驻点便可以解决大多数问题。
• 构造的辅助函数形式如下：

\[minf(x)+\mu \alpha (x) \]

• \(\mu\)为罚因子，大于0。

• 其中\(\alpha ( x ) = \sum _ { i = 1 } ^ { m } \phi \left( g _ { i } ( x ) \right) + \sum _ { j = 1 } ^ { 1 } \varphi \left( h _ { j } ( x ) \right)\)

• 通常令\(\phi(x)=[max{0,x}]^p\), \(\varphi (x)=|x|^p\), \(p\)值通常为\(2\)。

• 求解过程就是对辅助函数求驻点，并计算\(\mu\)趋近无穷大时，最优解的值。

5.3 闸函数法（内点法）

• 闸函数适用于不等式约束问题，即\((fg)\)问题。思想与罚函数基本相同。不同点在于该方法将惩罚家在约束集的边界，当靠近边界时，惩罚项无穷大。
• 构造的辅助函数形式如下：

\[minf(x)+\mu B(x) \]

• \(\mu\)为罚因子，大于0。
• 其中\(B ( x ) = \sum _ { i = 1 } ^ { m } \phi \left( g _ { i } ( x ) \right)\)
• 通常令\(\phi(x)= - \frac { 1 } { x }\)。
• 求解过程就是对辅助函数求驻点，并计算\(\mu\)趋近\(0^+\)时，最优解的值。