编码中遇到的这些字符串、整数、小数在计算机中是怎么存储的？

引发思考

我用Java语言，如下代码，创建了一个int类型、String类型与float类型，计算机存的就是1、“is a String”、3.625么

int i = 1;
String s = "is a String";
float f = 3.625;

可能我们在想，我不需要知道计算机怎么存的啊，我会用java的这几个基础类型就行了，计算机又不会给我弄错！

真的不会弄错么？

答案是：会，计算机还真的会弄错，这发生在浮点数的计算过程中，比如下面的计算：
4.0-3.6=？
我们都知道答案是0.4，但是计算机给出的答案可能是：
4.0-3.6=0.40000001
不会吧，计算机这么“蠢”？我奶奶都会算！（吐槽），哈哈哈，计算机会发生这样的精度计算差，这是由计算机的存储机制所导致的计算失误，要想避免这样的一个错误，我们就需要了解计算机是怎么存储一个数又是怎么参与计算的！

字节与十六进制

字节的由来，大概是1956年前后由IBM公司提出的，用来表示8位二进制数，为什么是8位，而不是6位，7位、9位呢？IBM采用字节是因为它们易于以BCD这种格式保存，而且用字节用来表示文本也是合适的，因为8位二进制数2^8可以代表256种事物中的一个，大多数的书面语言都可以用少于256个字符集来表示。字节为8位是技术发展过程中择优选择的结果。
十六进制，[1,2,3,4,5,6,7,8,9,A,B,C,D,E,F]，它的诞生是为了简洁明了的表示字节，因为1个8位二进制数实在太不简明了，例如11100111，10100100，来看看用十六进制来表示11100111 -> E7,10100100 -> A4，这就是十六进制带来的好处。

存储数字

"一个数字在计算机中都是以补码形式存储的"，要想理解这个概念，需要先了解补码、反码、原码是什么。在Java中我们数值型有四个类型，byte（1个字节）、short（2个字节）、int（4个字节）、long（8个字节），在计算机中也就是按这些字节数来存储的 ，就比如常用的int来说，在计算机中存储的就是4个字节32位，比如我们开头所列的表达式int i = 1,存储的二进制为00000000000000000000000000000001,不需要转换为补码，因为正整数原码、反码、补码都一样,这里可能会问，那么负数呢？int i = -1呢？负数需要进行补码转换，转换过程为10000000000000000000000000000001（原码） -> 11111111111111111111111111111110（反码） -> 11111111111111111111111111111111（补码）,在计算机中int型的-1存储的就是11111111111111111111111111111111。

存储文本

我们肯定接触过ASCII码字符编码集。先来理解它的作用，比如我们的一个文本is a String,其中包含了这些字符的i、s、a、S、t、r、n、g、space(空格),ASCII字符编码集就有一个对应表，对应着i、a等等这些字符对应的十六进制，我们通过查表转换为is a String -> 69(i)、73(s)、20(空格)、61(a)、20(空格)、53(S)、74(t)、72(r)、69(i)、6E(n)、67(g),这就是ASCII字符编码集的作用，它作为文本数据与二进制数据中的“翻译表”。is a String是全英文文本，我们的中文可以通过ASCII来进行“翻译”吗？可以，ASCII目前有很多的扩展，可以用来表示中文。但是我们常用的还是Unicode编码集，Unicode采用双字节（16位）编码，ASCII是7位，可以表示2^16=65536个不同字符，Unicode的可扩展性更好，给我们预留了很多的空间，对于中文这种复杂一点的语言，有更好的帮助。

存储小数

小数在计算机中是以浮点数的形式存储的，浮点数相对于定点数的概念，定点数的含义就是小数点的位置是固定的，比如999999.99与111111.11，都是倒数第三位为小数点位。而浮点数含义为小数点的位置是浮动的，不固定的。比如111111.11、0.0000011等
开头我们定义了一个单精度浮点数float f = 3.625,我们已知单精度浮点数存储为4个字节（可参考IEEE浮点数标准），我们将3.625（十进制小数）转换为二进制小数11.101，转换过程为整数部分与小数部分单独转换，整数部分为3 -> 3/2=1(余1) -> 1/2=0(余1)，小数部分0.625*2=1.25(取整数部分1) -> 0.25*2=0.5(取0) -> 0.5*2=1(取1)，将整数部分结果与小数部分结果整合得出结果为11.101，这就是用二进制来表示小数数字。那么在计算机中又是怎么存这个二进制的呢？
我们要提到科学记数法，如十进制中，可以用5.369952314 x 10^5的格式来表示小数，其中首位的5.369952314表示为有效数，10^5中的5表示为指数，在二进制中与之类似。单精度浮点数包括三部分，如下：

存储11.101用科学记数法的浮点格式则为11.101-> 1.1101 * 2^1，其中有效数为1101，e-127=1，指数e=128，符号位为0（因为为正浮点数），拼接起来则为0(占1位) 10000000(占8位) 00000000000000000001101(23位有效数)，这就是计算机中存储单精度浮点数3.14的最终二进制格式了。
回到开始，我们发现计算机计算4.0 - 3.6 = 0.40000001时有错误，这是怎么造成的呢？
4.0转成二进制为0 10000001 00000000000000000000000,3.6转成二进制为3.6 -> 11.1001 1001 1001 1001 1001 1001...，3.6转二进制，小数位无限循环，不能取尽，但是单精度浮点数与双精度浮点数都是有精度范围的。只能去精度范围内的数据。3.6=0 10000000 11001100110011001100110(单精度有效位为23位)，将4.0与3.6相减(浮点数运算)后的结果为0.01100110011001100110011，我们来看下0.40000001的二进制表示：

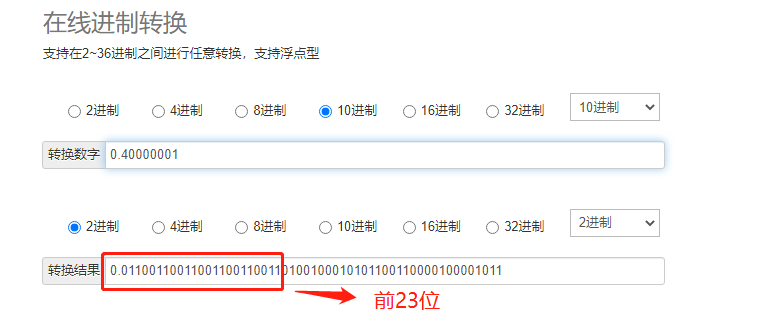
我们发现与4.0-3.6运算结果相同，这就是计算机中浮点数运算导致的精度误差。不仅仅是4.0-3.6,在浮点数计算中，会经常发现这种问题。

总结

1、计算机中存储任何数据都用的是二进制存储，且以字节为存储单位。
2、计算机中存储数字时，用补码来表示负数。
3、计算机中存储文本数据，是有一个文本字符与字节映射表，比如ASCII、Unicode等
4、计算机中存储小数用的是浮点数格式，结合科学记数法。且浮点数运算时会产生一些精度问题，用double双精度会避免一些精度错误，但是不能完全解决问题。计算机科学家们用了一个算法来解决，Kahan Summation，此算法原理就是在每次的计算过程中，都用一次减法，把当前加法计算中损失的精度记录下来，然后在后面的循环中，把这个精度损失放在要加的小数上，再做一次运算。