[论文笔记] Context-, Flow-, and Field-Sensitive Data-Flow Analysis using Synchronized Pushdown Systems

Introduction

传统的使用 AccessPath 的字段敏感分析在面临循环字段引用（cyclic field reference）时存在路径爆炸的问题，比如对于 JDK 8 中 TreeMap 的实现：

函数 rotateLeft 在函数 fixAfterInsertion 的 while 循环中被调用，rotateLeft 的 16, 17, 19, 20 行就是一个循环字段引用的案例。由于路径不敏感，静态分析会过近似地认为任意一个 由字段 left, right, parent 组成的任意长度的 AccessPath 都可能被写入 value，即 \(T = \{this.f_1.f_2. ... .f_n | f_k \in \{ \text{left, right, parent} \}, 1 \leq k \leq n \in N\}\)。

在实际实现中，静态分析使用 k-limit 限制 AccessPath 的长度，但这仍然导致巨大的开销。

SPDS 使用两个下推系统 field-PDS 和 call-PDS 解决字段敏感和上下文敏感，并同步他们的结果。把复杂度从 \(|\mathbb{F}^{3k}|\) 降低到 \(|\mathbb{S}||\mathbb{F}|^2\)。

A short introduction to pushdown systems

call-PDS

下推系统的定义如下：

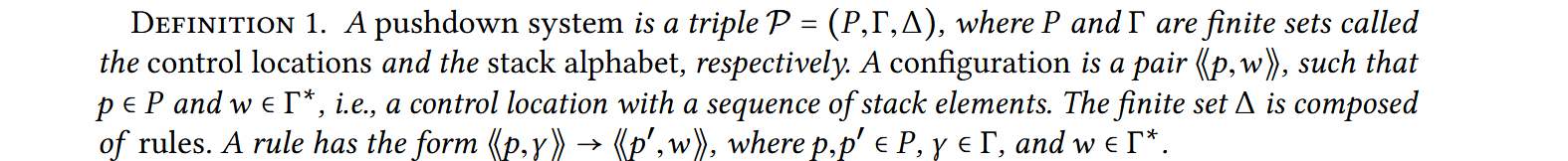
\(w\) 的长度 \(|w|\) 决定了规则是 push 规则，pop 规则还是 normal 规则，因为会用 \(w\) 作为新的栈顶元素取代 \(\gamma\)。

一个用于上下文敏感和流敏感数据流分析的 call-PDS 可以被定义为 \(\mathcal{P}_{\mathbb{S}} = (\mathbb{V}, \mathbb{S}, \delta_{\mathbb{S}})\)。\(\mathbb{V}\) 是程序变量，\(\mathbb{S}\) 是程序 statement。Normal 规则对过程内的 flow function 做建模，push 规则描述变量到参数的流动并处理上下文敏感，pop 规则描述被返回的变量到对应的 callsite 之间的流动。常规规则还可以使得 \(\mathcal{P}_{\mathbb{S}}\) 具有流敏感性。

下表给出了一个过程内的 flow function 的例子 assignFlow：

表中涵盖了四种情况：第一种情况表示正在追踪变量 \(x\) 但 \(x\) 的旧数据流已经被新的数据流覆盖，所以返回空集表示不再追踪；第二种情况表示正在追踪变量 \(y\)，\(y\) 又被赋值给了 \(x\)，所以接下来需要同时追踪 \(x\) 和 \(y\)，返回集合 \(\{x, y\}\)；assignFlow 是字段不敏感的，所以对于最后两个情况，输出的集合都是 \(\{x, y\}\)。

对于 statement \(s\)，如果控制流下一个 statement 是 \(t\)，那么对于 \(assignFlow(x, t)\) 中返回的集合中任意一个元素 \(y\)（原文是 \(assignFlow(x, s)\) 但是这个下面的例子，以及 flow function 的目的对应不上，所以我认为是错误的），都有一个对应的 normal 规则 \(\langle \langle x, s \rangle \rangle \rightarrow \langle \langle y, t \rangle \rangle\)。

下面给出了一个过程间数据流的例子：

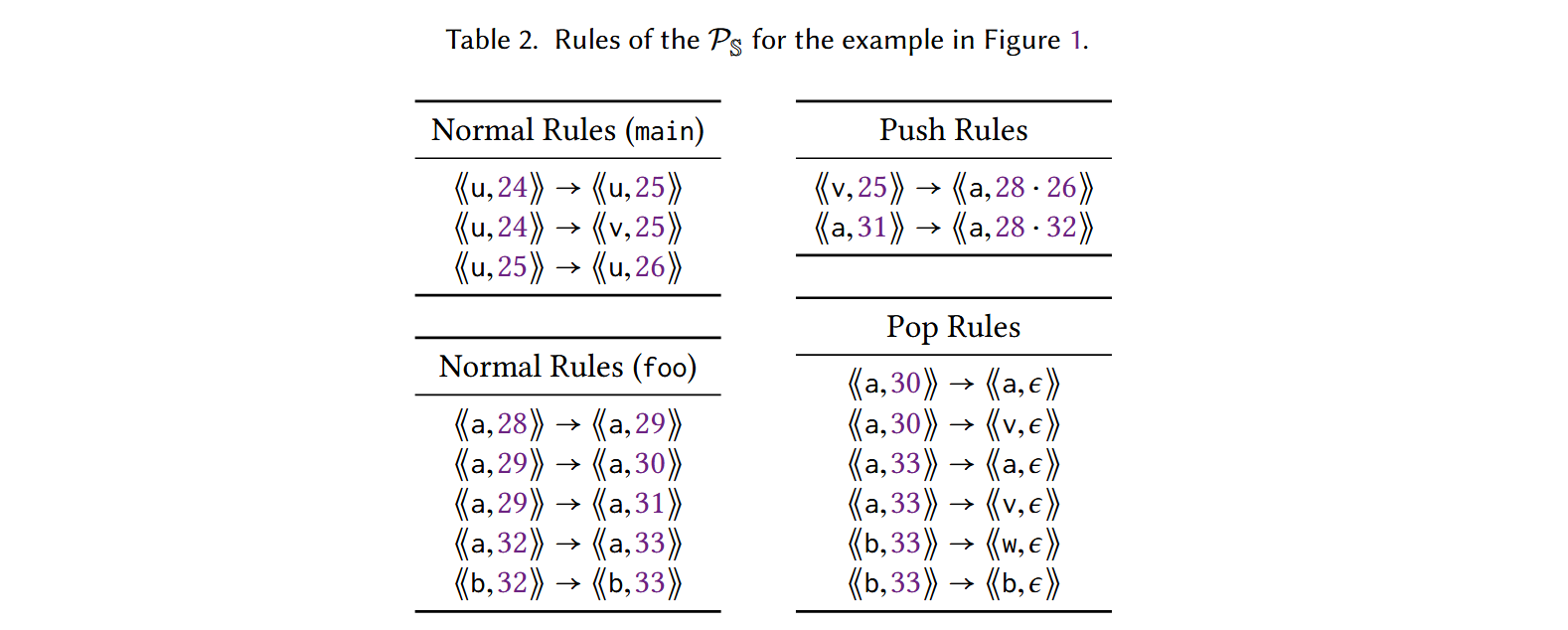
Normal 规则比较简单，不再做解释。第一条 push 规则 \(\langle \langle v, 25 \rangle \rangle \rightarrow \langle \langle a, 28 · 26 \rangle \rangle\) 表示当数据流到达第 25 行的变量 \(v\) 时，流动将从第 28 行的语句继续。每当从栈中弹出一条语句时，流动仍在第 26 行的 callsite 之后保持有效，弹出即一个 pop 规则，对应 \(return\) 语句。

call-PDS 上存在转移关系：如果 \(\langle \langle p, \gamma \rangle \rangle \rightarrow \langle \langle p', \omega \rangle \rangle\)，那么对于任意的串 \(\omega'\) 都有 \(\langle \langle p, \gamma \omega' \rangle \rangle \rightarrow \langle \langle p', \omega \omega' \rangle \rangle\)，这个转移关系刻画了 PDS 在栈上做的操作。从一个起始 configuration \(c\) 出发，不断应用规则，可以得到一个 \(c\) 可达的 configuration 集合 \(post*(c) = \{c' | c \Rightarrow^* c'\}\)（\(\Rightarrow^*\) 表示传递闭包）。这个集合可以用正则表达式描述。

自动机 \(\mathcal{A}\) 描述了可达 configuration 集合。有算法 \(post*\) 可以以一个只接受初始 configuration 的自动机和一组规则为参数，构建出自动机 \(\mathcal{A}\)。

如果我们想知道“从语句 s 处的变量 v 开始，数据会流到哪里去？”。我们构建一个只接受格局 \(\langle \langle v, s \rangle \rangle\) 的初始自动机，然后使用 \(post*\) 算法，检查 \(\langle \langle v, s' \rangle \rangle\) 是否被最后的自动机接受就可以了。对于上面的例子可以构建自动机：

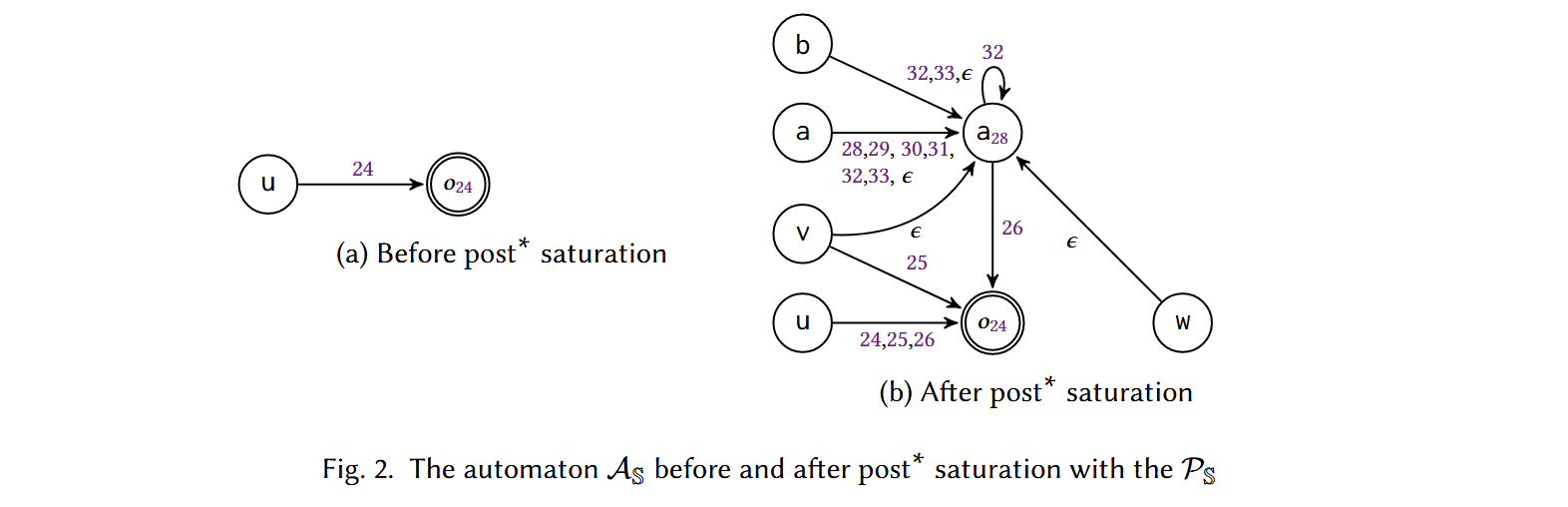
假设要追踪 24 行创建的对象，自动机首先接受 configuration \(\langle \langle u, 24 \rangle \rangle\)，状态 \(o_{24}\) 指 24 行创建的对象，这个初始自动机可以理解成：查询 24 行的 \(u\) 指向哪个对象，结果是 24 行的 \(o\)。具体的构建过程可以参考论文，但论文并没有给出规则和自动机构建之间的对应关系，因此对 push/pop 的描述不清楚。

Field-PDS

Field-PDS 是本文的第一个贡献。

类似的，\(\mathcal{P}_{\mathbb{F}}\) 的 configuration 是 \(\langle \langle x @ s, f_0f_1...f_n \rangle \rangle\)，可以被理解为从 statement \(s\) 之后，追踪 \(x.f_0f_1f_n\) 的流。对于 normal 规则的描述仍然借助一个函数：

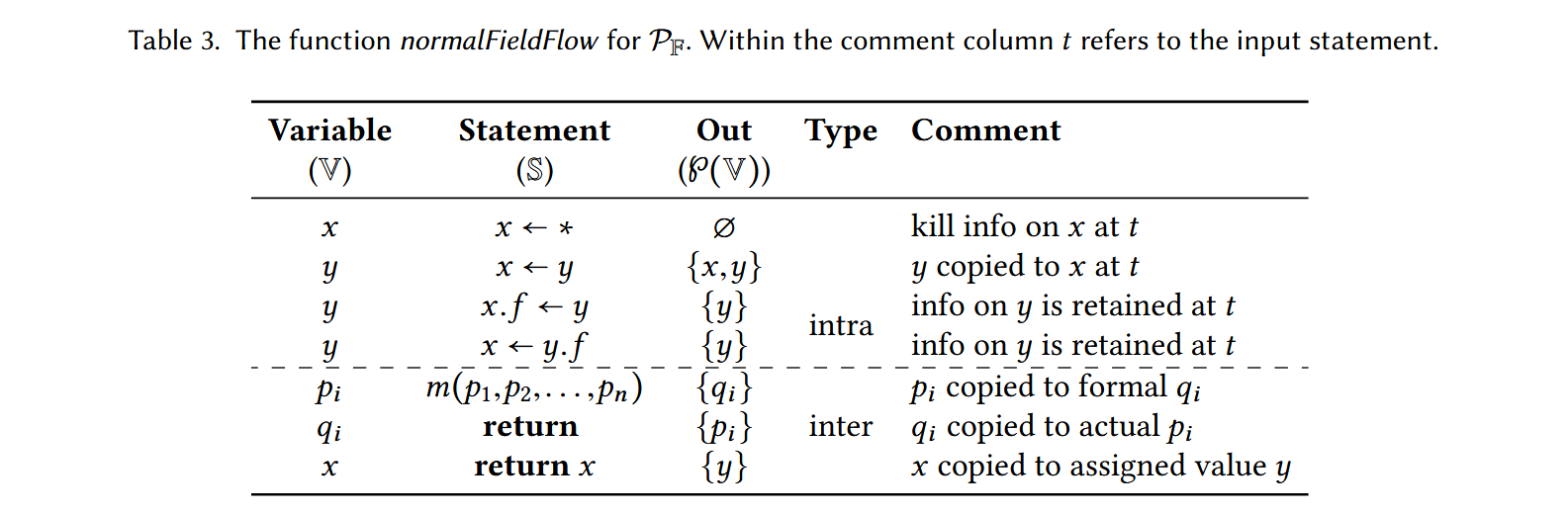
如果当前的 statement 是 \(s\)，控制流上的下一个 statement 是 \(t\)，对于每个 \(y \in normalFieldFlow(x,t)\) 都有一条匹配的 normal 规则：\(\langle \langle x @ s,g_0 \rangle \rangle \rightarrow \langle \langle y@t', g_0 \rangle \rangle\)，\(t' = t\) 除非 \(s\) 是一个 callsite 或者 return 语句，如果是 callsite，那么 \(t'\)

图中对于 \(x.f \leftarrow y\) 和 \(x \leftarrow y.f\) 并没有对字段做任何处理，这会通过一个额外的 push/pop 规则来描述。比如 \(x \leftarrow y.f\)，normal 规则是 \(\langle \langle y @ s,g_0 \rangle \rangle \rightarrow \langle \langle y@t, g_0 \rangle \rangle\)，还会有一个相应的 push 规则 \(\langle \langle y @ s,g_0 \rangle \rangle \rightarrow \langle \langle x@t, f \cdot g_0 \rangle \rangle\)。对于 \(x.f \leftarrow y\)，那么就有一个 pop 规则 \(\langle \langle y @ s,f \rangle \rangle \rightarrow \langle \langle x@t, \epsilon \rangle \rangle\)。相应地，自动机 \(\mathcal{A}_{\mathbb{F}}\) 的状态是变量和 statement，转移边是字段名。

例子如下：

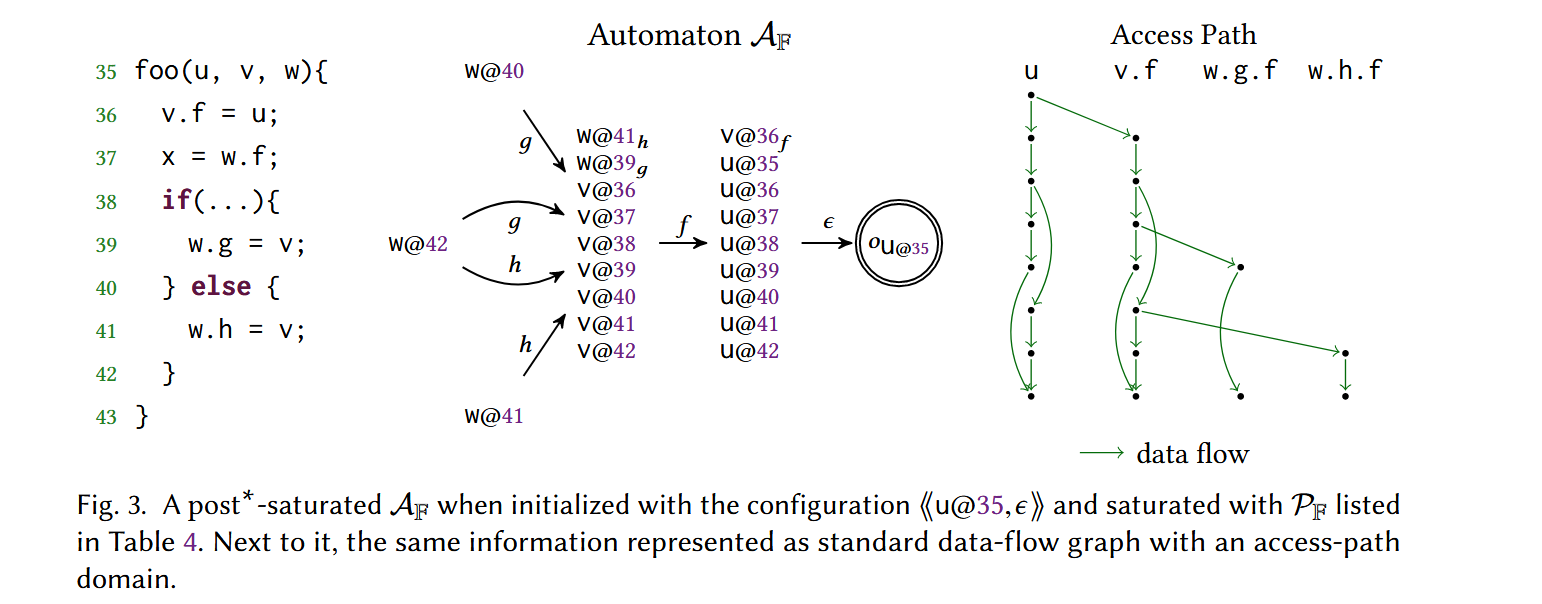
下面的例子展示了 while 语句内部的循环字段引用，及其规则的一个子集：

Normal 规则 \(\langle \langle a @ 48, * \rangle \rangle \rightarrow \langle \langle a @ 45 \rangle \rangle\) 对 while 循环做了建模，把 \(a\) 的新值传播到循环开始。通过上述方式可以观察到 field-PDS 及其对应的自动机是如何处理这种复杂的字段使用的。

Synchronized pushdown systems

本文的第二个贡献是结合 call-PDS 和 field-PDS 的结果，即 SPDS。

Call-PDS 和 field-PDS 合并的主要思路与普通自动机合并的思路一致。一个新的 configuration 可以被新的自动机 \(\mathcal{A}_{\mathbb{S}}^{\mathbb{F}}\) 接受当且仅当在原先的两个自动机中对应的子 configuration 都被接受。

一个样例代码及其图形化表示如下：

假设一个上下文敏感、流敏感和字段敏感的数据流分析，跟踪 51 行的变量 u 指向的对象，记为 \(o_{u@51}\)，那么有下面两个自动机：

假设有一个查询：变量 y 能否访问变量 u 指向的对象？根据上面的两个自动机可知，configuration \(\langle y, 55 \rangle\) 虽然被 \(\mathcal{A}_{\mathbb{S}}\) 接受，但 configuration \(\langle y@55, \epsilon \rangle\) 却不被 \(\mathcal{A}_{\mathbb{F}}\) 接受，因此答案是否。

但是 SPDS 仍然是一个过近似的分析，比如例子：

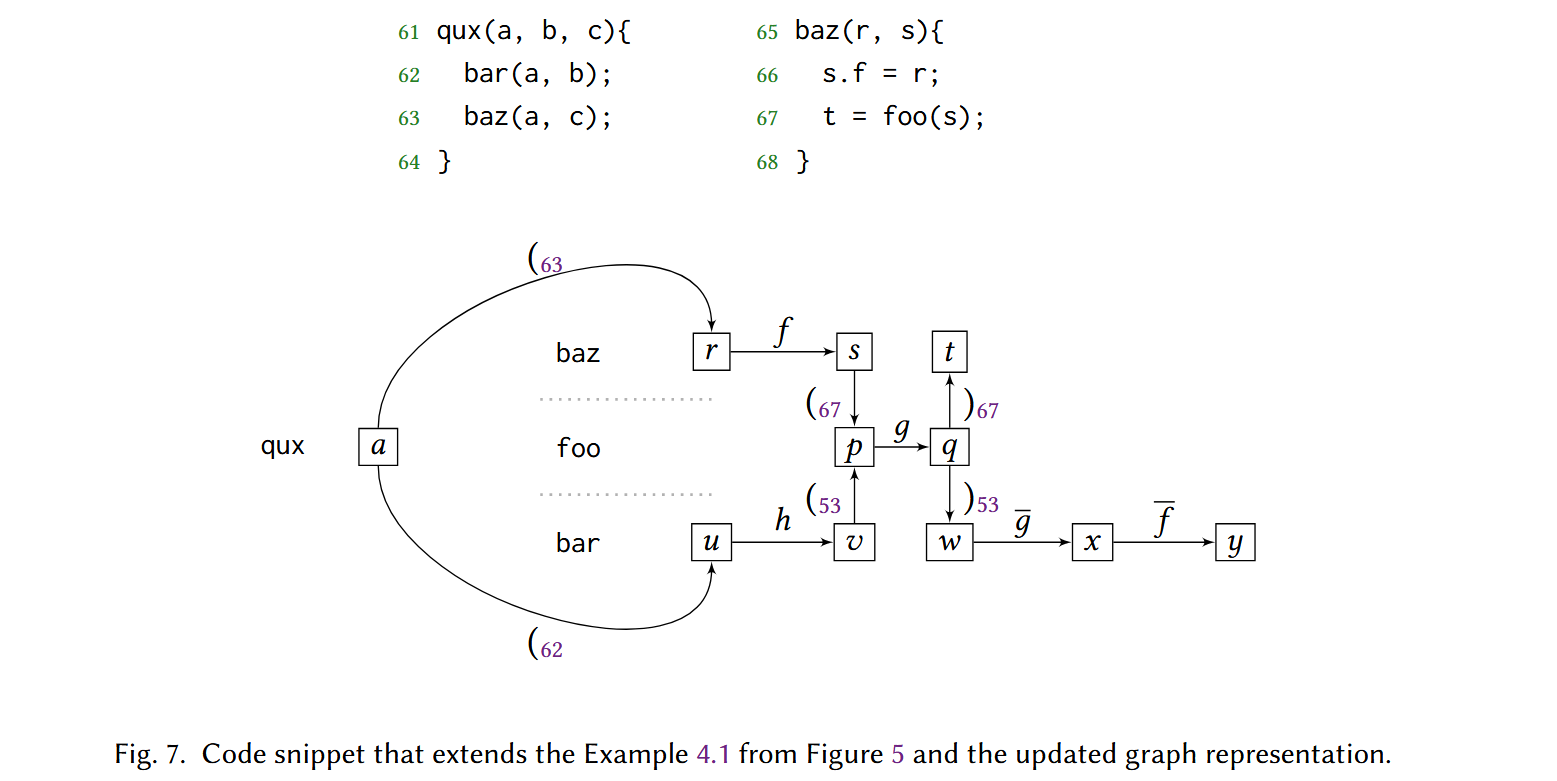
假设一个查询：是否存在从变量 a 到变量 y 的数据流？从图形化表示可以观察到从 a 到 y 有两条路径。一条是上下文调用栈合法但是存取字段不合法的，另一条是存取字段合法但是上下文调用栈不合法的，SPDS 会判定存在，但在实际运行中并不存在这样的路径。

复杂度分析

Instantiations of SPDS

指针分析是 non-distributive 的，难以直接使用 SPDS 进行分析。文章提出了一种方法，对每个对象的分配点单独使用一个 SPDS 进行分析，在遇到引用拷贝比如 \(x = y\) 时与其他 SPDS 交换 \(x\) 和 \(y\) 是别名的信息，然后在数据流图中添加间接边，比如：

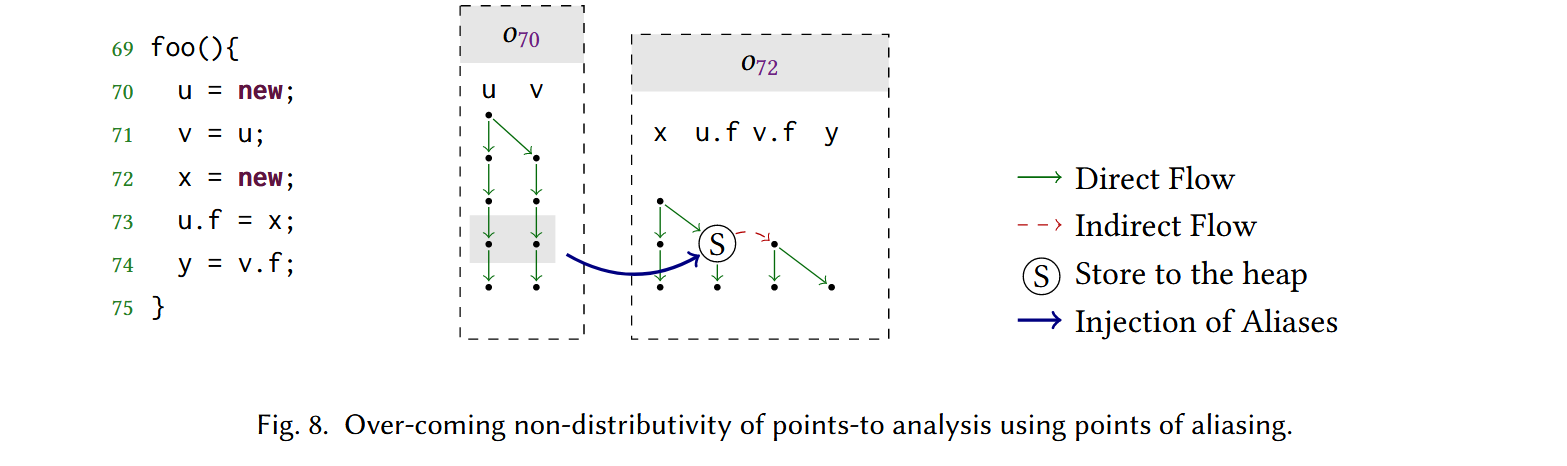
对于 typestate analysis，可以使用带边权重的 WPDS，把类型信息编码成边权重。对于按需分析，先通过一个反向分析确定程序切片，然后再使用 SPDS 进行正向分析。

Boomerang

Updating...