[论文笔记] On-Demand Strong Update Analysis via Value-Flow Refinement

Background

这一部分介绍了 llvm 中的 partial SSA 和 SVFG

程序先通过 partial SSA form 进行转换。所有变量的集合标识为 \(\mathcal{V}\)，address-taken 变量表示为 \(\mathcal{A}\)，top-level 变量表示为 \(\mathcal{T}\) 。经过 parital SSA 转换后，程序被五种 statement 表示：取地址 \(p=\&a\)，复制 \(p=q\)，取值 \(p=*q\)，存值 \(*p=q\)，Phi 函数 \(p=\Phi(q,r)\)。一个 swap 的 c 语言程序及其 SSA 如下：

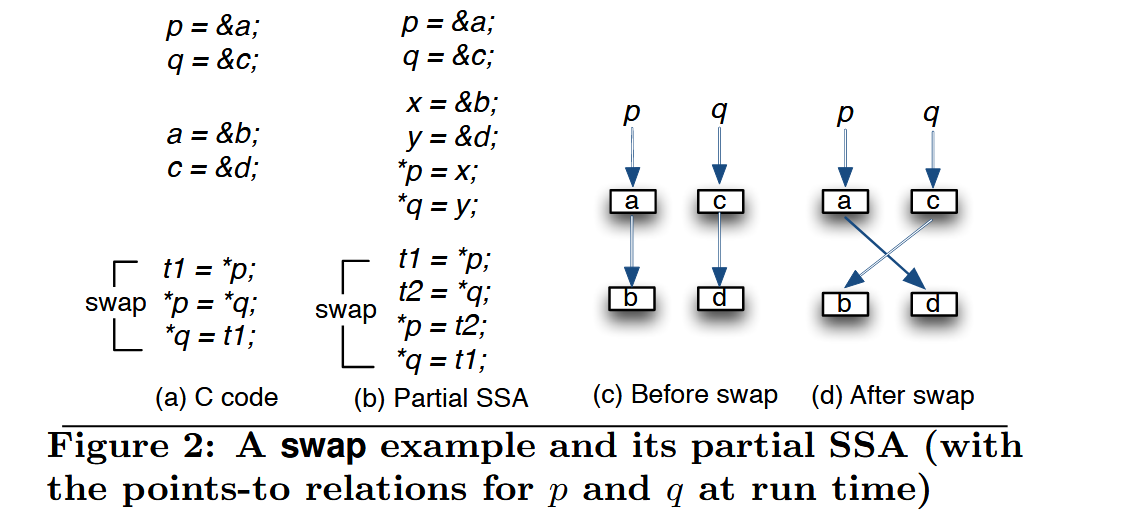
一个稀疏值流图（sparse value flow graph，SVFG）\(G=(N,E)\) 是一个有向重图，保守地捕捉 def-use 链。一个边 \(\mathcal{l_1} \stackrel{v}{\rightarrow} \mathcal{l_2}\) 意味着 statement \(\mathcal{l_1}\) 和 \(\mathcal{l_2}\) 之间有一个变量 \(v\) 的 def-use 关系。对于 top-level 变量，他们的 def-use 关系无需通过指针分析就能找到。

Address-taken 的变量要复杂一些，因为使用 partial SSA 使得它们并没有被 SSA 处理，可能有间接的 store 的情况，比如：

*q = 10; // store
*x = &q; // get addr
*x = 20; // store, indirectly
p = *q; // use

首先通过预分析得到程序的 point-to 信息。其次，对于每个可能被 \(q\) 指向的 address-taken 变量 \(a \in \mathcal{A}\) 用类似 memory SSA 的方式处理，一个 load \(p=*q\) 会被标记为 \(p=\mu(a)\) 来表示对变量 \(a\) 的潜在使用。类似的，对于每个可能被 \(p\) 指向的 address-taken 变量 \(a \in \mathcal{A}\)，一个 store \(*p=q\) 会被标记为 \(\chi(a)=q\)。然后，把每个 address-taken 变量转化为 SSA 形式，每个 \(\mu(a)\) 作为 \(a\) 的使用，每个 \(\chi(a)\) 作为 \(a\) 的定义和 \(a\) 的使用。最后提取 \(a\) 的间接 def-use 链，对于 SSA 后第 \(n\) 个版本的 \(a_n\)，在 \(\mathcal{l}'\) 处被定义，在 \(\mathcal{l}\) 处被使用，那么就标记 \(\mathcal{l} \stackrel{a}{\rightarrow} \mathcal{l}'\) 作为一个间接 def-use 链。

如果 \(a\) 是强更新 strong-updated 的，那么新的指向关系会取代旧的指向关系，否则是弱更新 weak-updated 的，会在旧的结果和新的结果之间取 join。

A motivating example

示例程序如下：

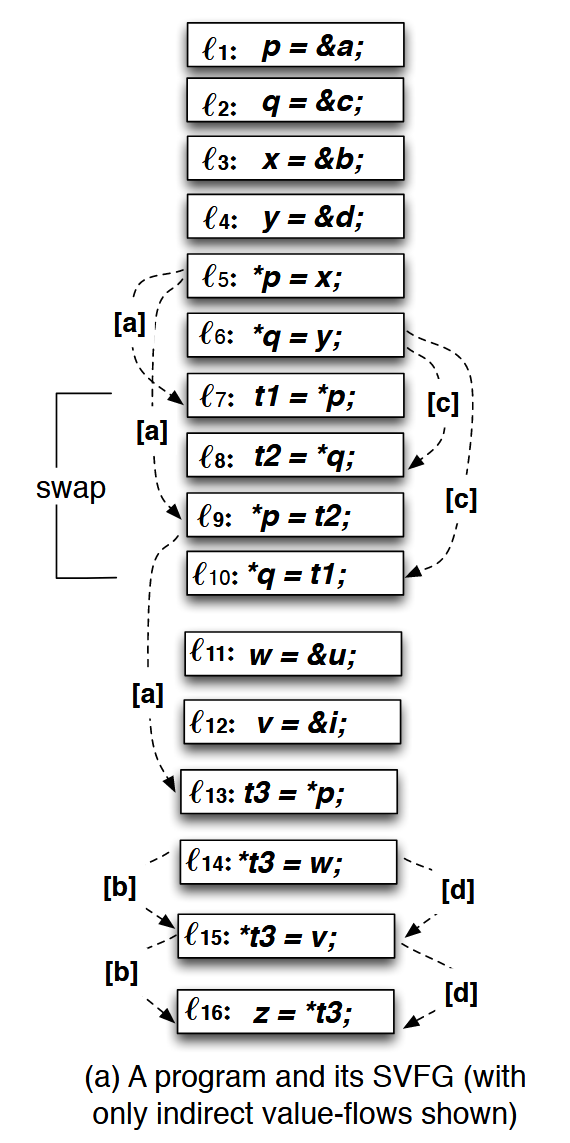
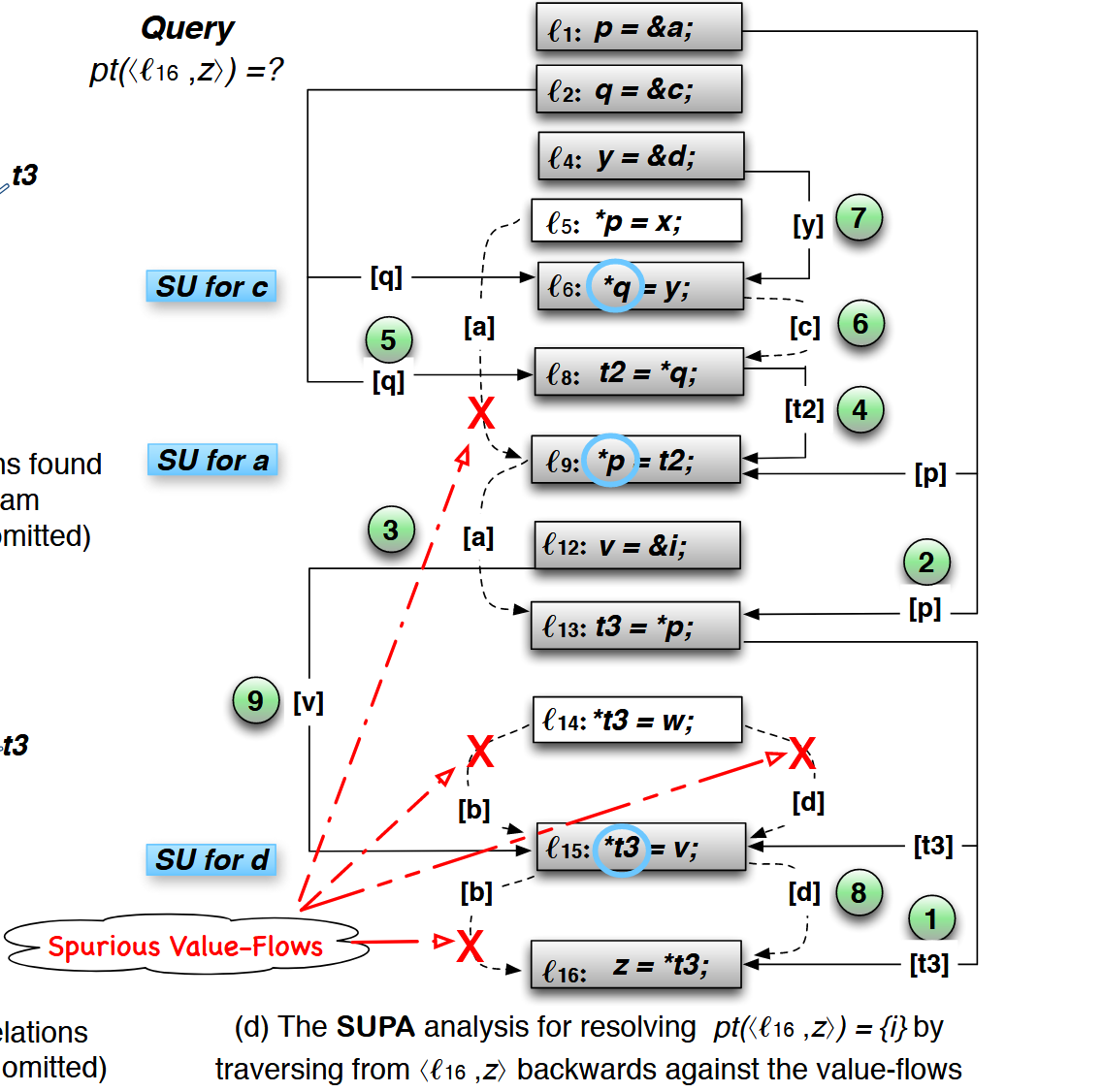
\(\mathcal{l_1}\) 到 \(\mathcal{l_{10}}\) 来自于上一节的 swap，为了表现 SUPA 的性质又额外添加了几行。假设 \(\mathcal{u}\) 是没有初始化的，但是 \(\mathcal{i}\) 是已经初始化的。接下来会说明 SUPA 怎么通过按需查询（Query：\(pt(\langle \mathcal{l_{16}}, z \rangle) = ?\)） \(\mathcal{l_{16}}\) 的 \(\mathcal{z}\) 仅仅指向初始化的 \(\mathcal{i}\)。

下图展示了流敏感并且强更新的分析在程序上的运行结果：

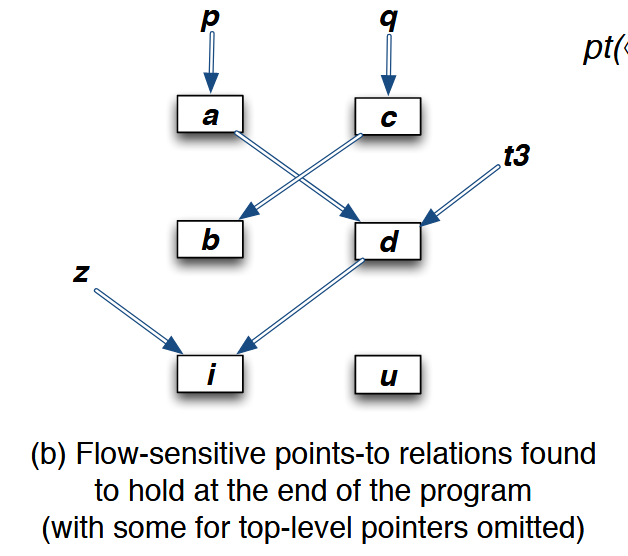
下图展示了一个流不敏感并且缺乏强更新的分析（Andersen 风格指针分析）是怎么过近似结果，引入大量的虚假指向关系的：

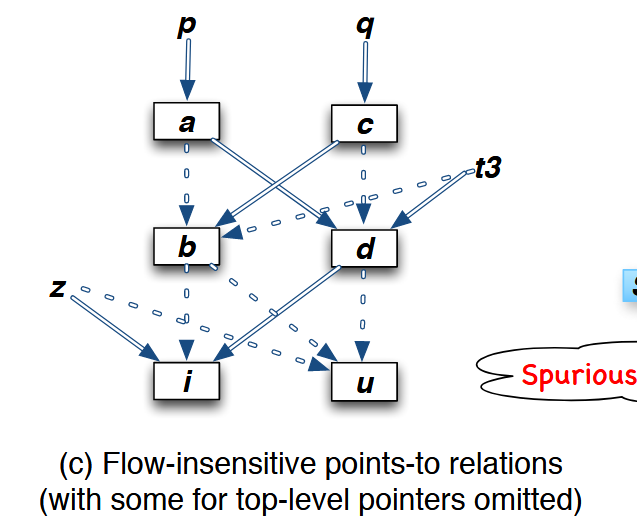
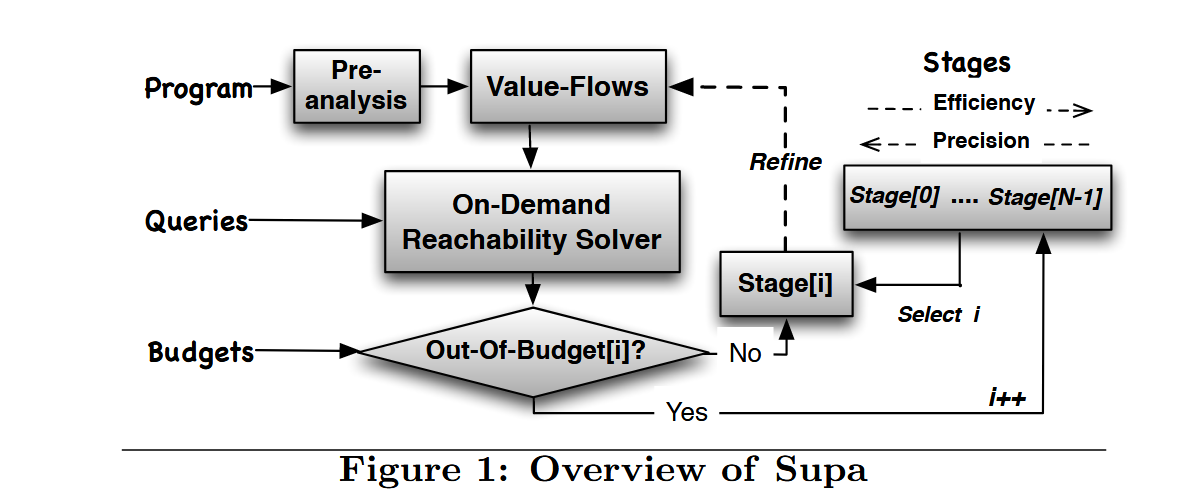
SUPA 的 workflow 如下。SUPA 通过混合多阶段的分析细化不精确的预分析产生的值流，如果上一个阶段超出了时间或者空间预算，那么就在下一个阶段进行一个更加不精确但是更加可扩展的分析：

SUPA 会首先执行一个预分析来构建 figure (a) 中的 SVFG。对于 top-level 变量，def-use 关系是显式的并且很容易识别，比如 \(q\) 就有 \(l_2 \rightarrow l_6\) \(l_2 \rightarrow l_8\) \(l_2 \rightarrow l_{10}\) 三个 value flow。对于 address-taken 变量，首先使用一个流不敏感的 Andersen 风格分析得到一个过近似的不精确结果。然后得到间接值流。以变量 \(b\) 为例，因为 \(t_3\) 指向 \(b\)，所以 \(l_{14}, l_{15}, l_{16}\) 会被分别标记成 \(b=\chi(b), b=\chi(b), b=\mu(b)\) 。然后会对 \(b\) 应用 SSA，得到 \(b_2=\chi(b_1), b_3=\chi(b_2), \mu(b_3)\)，然后有 \(l_{14} \rightarrow l_{15}\) \(l_{15} \rightarrow l_{16}\)，最终的间接值流如 figure (a) 所示。

SUPA 接下来的工作如图，暂时还没办法解释：

Demand-driven strong updates

目前 SUPA 由两个阶段组成，FSCS（flow-sensitive and context-sensitive）和 FS，因此下面按顺序介绍 flow-sensitivity、context-sensitivity 和混合分析的 formalism。

定义 \(\mathbb{V} = \mathcal{L} \times \mathcal{V}\) 表示变量及其对应的 statement 标记，比如 \(\langle \mathcal{l_{16}}, z \rangle\) 表示第 16 个 statement 的变量 \(z\)。可达性关系 \(\hookleftarrow \subseteq \mathbb{V} \times \mathbb{V}\)，\(\langle l, v \rangle \hookleftarrow \langle l', v' \rangle\) 表示 \(l'\) 处 \(v'\) 的 def 通过若干值流边可以到达 \(l\) 处 \(v\) 的 use。对于通过 \(l'\) 处 ADDROF 创建的对象 \(\langle l', o\rangle\) 简记为 \(\hat{o}\)，可以看成一种“地址对象”。

假设 top-level 变量对应的值流是精确的。当处理 LOAD \(p = *q\) 时，反向遍历 SVFG 找到 \(q\) 的 def 位置，然后找到给 \(q\) 赋予指针别名的对象 \(\hat{o}\)，再找到 \(o\) 的 def 位置，最终确立一个新的可达关系。STORE 的处理类似。规则 SU/WU 用来对强弱更新进行建模。定义 kill 集合 \(kill(l, p)\)，如果 \(pt(\langle l, p \rangle)\) 有指向，那么就可以杀死旧的值 \(o'\) 用新的 \(o\) 进行强更新，如果没有指向，则不应该建立任何的可达性关系以避免空指针解引用。

延续上面的例子：

Updating...