[论文笔记] Static Analysis with Demand-Driven Value Refinement
Introduction
JavaScript 的动态特性使静态分析变得困难。近期工作提出了很多方法 uniformly 提升 JavaScript 分析的精度,比如 high degrees of context sensitivity,aggressive loop enrolling,sophisticated abstract domains for string。这里的 uniformly 是指上述方法在程序的任何一个位置都会在相同程度上提升分析精度。作者认为这种 uniform 的方法并不适用于解决 JavaScript 静态分析的精度问题。对此作者提出了一种 demand-driven value refinement 来在 JavaScript 程序的特定位置引入精确性的提升。工作受到 Thresher: Precise Refutations for Heap Reachability, PLDI'13 的启发。
Motivating example
函数 mixin 把 source 中的函数对象复制到 object 中,如果 object 是一个函数,那么还会复制到 object 的原型上。

下面是使用函数 mixin 的一个例子:baseFor 接受一个对象 object 和函数 iteratee 作为参数,然后递归地在对象的所有字段上执行 iteratee;24-32 行的匿名函数通过调用 baseFor 把 lodash 上所有不在原型上的方法复制到新的对象 source 中。

图中绿色标记的都是动态字段读写对,被称为 field copy or transformation(FCT): x[a]; y[b] = v;,其中 b 是 a 的函数,v 是 x[a] 的函数,这种模式是 correlated read/write pattern 的一种推广形式,correlated read/write 要求 a 和 b 严格相等。动态字段读写的精度对于 JavaScript 的静态分析尤其重要,否则可能会导致 lodash 的所有字段混合在一起,而几乎丧失对使用了 lodash 库的 JavaScript 程序的分析能力。现有的分析工具不能够解析出例子中 methodName 的精确值,或者精确的识别例子中相关的读写对。
Value refinement 会在遇到不精确的属性写入时触发,通过细化不精确的对象的抽象域恢复分析精确性。比如③ methodName 映射到表示任意字符串的抽象值,func 映射到抽象所有 Lodash 函数的抽象值。然后,我们将 func 分解为精确的 partition,每个函数一个,然后通过 value refinement 以获取函数对应的可能属性名称。恢复该关系信息后,使得 lodash.map 函数被分配给 source["map"],lodash.filter 被分配给 source["filter"]。
Value refinement 通过基于抽象解释的反向分析完成。给定一个程序位置 \(l\),一个变量 \(y\) 和一个约束 \(\phi\),反向分析应当计算出 \(y\) 在满足 \(\phi\) 的情况下在 \(l\) 处的 a bound on the possible values。反向分析是基于当前的调用图进行的,不需要调用图达到不动点,这在后面被证明是 sound 的。
A simple dynamic language and dataflow analysis
Language 的文法和指称语义如下:

这个 language 对应的程序被描述为一个控制流图 \(\langle l_0, T \rangle\),\(l_0\) 是初始代码行,\(T\) 是边集

内存位置可以是变量,也可以是对象地址及其某个字段对应的字面值构成的元组,值可以是字面量,也可以是对象地址,状态 \(\sigma\) 是内存位置 \(Mem\) 到值 \(Val\) 的一个部分函数,记号 \(\sigma [m \mapsto v]\) 指一个和 \(\sigma\) 几乎相同的状态,但是内存 \(m\) 指向新的值 \(v\),辅助函数 \(fresh\) 返回一个新的对象地址
根据上面的定义,可以进一步定义整个程序的语义:

第一条规则说明空状态 \(\epsilon\) 是可达的,第二条规则说明状态如何在控制流图上做转移
数据流分析通过单调性框架描述(lattice 和 monotone transfer function),lattice 定义如下,是 TAJS 的一个简化版本:

图中缺少了一部分 lattice 的描述:如果使用 allocation site 刻画对象位置,那么 \(\hat{a}\) 就表示位置抽象,\(\hat{Addr}\) 代表位置抽象的集合(lattice 值)即 \(\hat{Addr} = \{o_{line \ 1}, \ o_{line \ 2}, \ ...\}\),\(\hat{A} = \mathcal{P}(\hat{Addr})\)
\(\hat{Val}\) 的 lattice 值是对象地址的幂集和字面值构成的乘积 lattice;\(\hat{a} \prec_1 \hat{v}\) 指代抽象值 \(\hat{v}\) 的具体值的第一个分量在集合上包含抽象对象地址 \(\hat{a}\),类似的对于第二个分量字面值有 \(\hat{p} \prec_2 \hat{v}\)
对于控制流图的每个边都定义一个转移函数 \(\tau_{l \rightarrow_s l'}: \hat{State} \rightarrow \hat{State}\),如果 \(s\) 对应 \(x[y]=z\),那么有:

对于状态 \(\hat{\sigma}\),如果里面有内存 \(\hat{m}\) 是对象及其字段 \((\hat{a}, p)\) 并满足 \(\hat{a} \prec_1 \hat{state}x\) 和 \(\hat{p} \prec_2 \hat{state}x\)(此时 \(p\) 的具体值和抽象值相对应,我不确定作者是不是喝醉了),那么就更新这个内存的指向,取最小上界
案例:

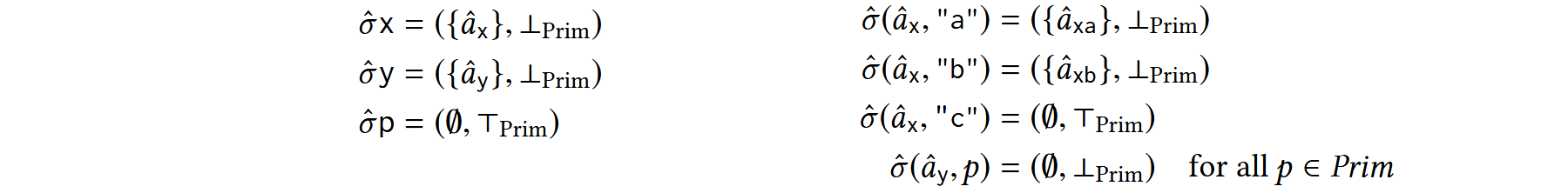
因为 p 的值不确定,所以 t 会被认为是 x 的所有字段的值的最小上界,然后 t 再被赋值到 y 的每个字段,这就引入了不精确性,本来应该是 x 和 y 的同名字段之间做拷贝。这个例子可以和下面这个伪代码做个对应,p 的值不确定因为来自于 array 和未建模的库调用:
for key in Object.keys(x) {
t = x[key];
y[key] = t; // imprecision
}
// input: x = { "a": 1, "b": 2 }
// output: t = Top ("Top" is lub of "1" and "2")
// y = { "a": Top, "b": Top }
Demand-driven value refinement
一个 value refiner 定义为一个函数 \(R: Loc \times Var \times Constraint \rightarrow \mathcal{P}(\hat{Val})\),constraint 被定义为 \(Constrant = Var \times \hat{Val}\) 。为了 soundness,要求 value refiner 是过近似的。暂时考虑把 value refiner 看成一个黑盒,先讨论它的用法。
先重点关注动态字段写入这种操作。首先定义一个辅助函数 partition \(Part: Val \rightarrow \mathcal{P}(\hat{Val})\),它把一个抽象值分割成若干抽象值的集合,可以看作是在 lattice 上往下分解

然后考虑一个新的转移函数 \(\tau_{l \rightarrow_s l'}^{VR}\) 来把上面的 value refiner 融入到数据流分析中,仍然考虑 \(x[y]=z\)


当 \(y\) 的值不精确并且 \(z\) 的值可以被划分成超过一个值时,value refiner 会被应用。应用 value refiner 时,会对 \(z\) 的值的每个划分做查询,然后取最小下界作为要更新的值。
继续使用上面的例子:

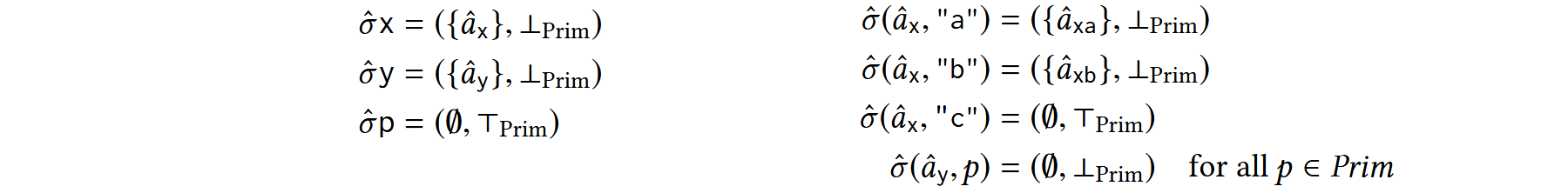
\(t\) 会被切分成三个值,然后对这三个值做查询,得到匹配的字段值之后再把切分后的值写入到字段。可能需要结合例子和定义体会 partition 的意义和 value refiner 的用法。
Backwards abstract interpretation for value refinement
这一节会给出 value refiner \(R^{\leftarrow}\) 的定义。\(R^{\leftarrow}\) 从触发 value refinement 的状态反向探索,使用一个基于分离逻辑的抽象域过近似那些可达该状态的所有状态。

这里的 symbolic variables \(\hat{x}\) 应该可以理解成抽象推理过程中使用的变量?
Heap constraints 通过 intuition separation logic 定义。在这种情况下,类似于 \(x \mapsto \hat{x}\) 这种单内存位置的 heap constraints 不止在仅包含该内存位置的堆区域上成立,对于任何包含该单元的堆区域都成立。那么新的 heap constraints 不会使得旧的 heap constraints 失效,这就带来了一种单调性。\(\phi \land \phi'\) 的过程中包含 alpha-renaming 和 re-normalization。
Valuations 是一组映射,把符号变量映射回一个具体的值。函数 eval 接受一个符号表达式和映射作为参数,计算符号表达式的具体值。\(\gamma_{val}(\hat{v})\) 是上一节提到的抽象值 \(\hat{v}\) 的具体化。


根据 refutation sound 的 Hoare triples 来定义 backward analysis。定义如下:

引入一个符号变量 \(RES\) 表示需要细化的变量。对于一个查询 \(R^{\leftarrow}(l, x, y \mapsto \hat{v})\),首先把这个查询编码成 \(x \mapsto RES * y \mapsto \hat{y} \land \hat{y} = \hat{v}\),然后反向应用 Hoare 三元组。用之前的例子说明:
对于 \(t\) 被切分出来的第一个值,有查询:\(R^{\leftarrow}(l_2, p, t \mapsto (\{\hat{a}_{xa}, \perp_{prim} \}))\),那么有:

现在继续对 \(R^{\leftarrow}\) 做扩展,构建一个以数据流分析中的抽象状态 \(X\) 为参数的 value refiner \(R^{\leftarrow}_X\),通过该过程把符号存储和抽象状态 \(X\) 结合起来增强符号存储的细化能力:如果 \(R^{\leftarrow}_X\) 有一个符号存储 \(\phi\) 要精化一个字段名称,同时该字段的值有约束时,value refiner 就会访问数据流分析的抽象状态并决定一组可能的属性名。这个过程叫 property name inference。
沿用上面的例子,现在的 \(\phi\) 是:
那么就可以使用数据流分析的结果直接推断 \(RES\):
得到结果 \(\{(\emptyset, "a")\}\)
Evaluation
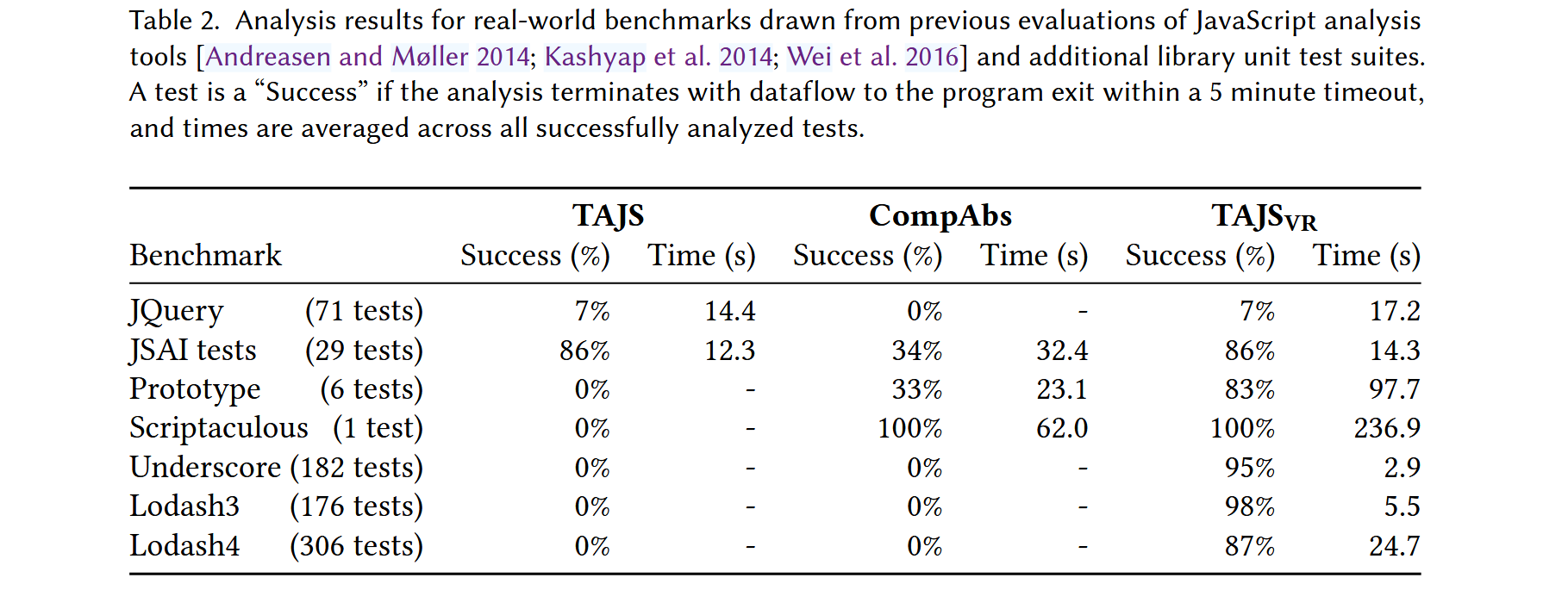

读后感:对于初入程序分析的新手来说简直是雄文。复杂的符号定义之后的主要思想还是比较直接:当某个具有多于一种可能的值将被写入到某个对象的多余一个字段时,考虑值的每种可能性,反向利用 separation logic 和 hoare logic 推断值的来源。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号