16 - Metatheory of subtyping

Subtyping 提到的规则并不适合实现，原因在于 T-SUB 和 S-Trans 规则推导中的项 \(t\) 没有任何约束的元变量（没有对形状作出限制）。

这意味着对于任意一个项 \(t\)，无法确定在什么时机使用什么规则做类型推导。

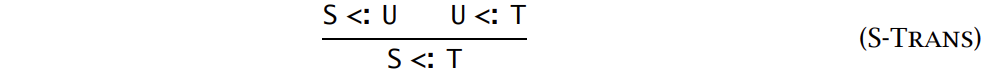
S-Trans 的另一个问题是，\(U\) 的搜索空间近乎无穷大。解决所有这些问题的方法是：用两种新的关系，算法子类型关系 algorithmic subtyping 和算法类型关系 algorithmic typing，来替换普通的子类型和类型关系。然后证明这种替换是正确的。

类型检查器 type checker 会调用子类型检查器 subtype checker 判断 \((S, T)\) 是否满足 \(\mapsto S <: T\)，即 \(S\) 和 \(T\) 是否满足算法子类型关系。算法子类型关系中省略了 S-Trans 和 S-Refl 规则。

关于 record 的 width，depth 和 permutation 规则被合并成一个规则 S-RCD：

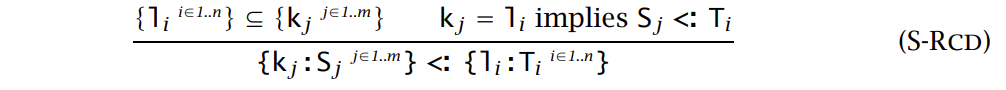
引理：证明 S-RCD 和原先的三个规则是等价的

引理：证明 S-REFL 和 S-TRANS 在只包含函数类型和 record 类型的子类型系统中是不必要的

证明 1 ：

对 S 的类型进行归纳：

• Top：通过 S-Top 自然成立

• 函数类型：通过 S-ARROW 规则对 \(T_1\) 和 \(T_2\) 做归纳

• record：通过 S-RCD 自然成立

证明 2：

对推导过程进行归纳，考虑最后一条被应用的规则：

• 不是 S-TRANS：对剩余的规则继续归纳

• 是 S-TRANS：那么存在 \(S <: U\) 和 \(U <: T\) 两个子推导，同时讨论这两个子推导的最后一条规则：

• 任意一个规则 + S-Top 或者 S-Top + 任意一个规则可以直接替换成 S-Top

• S-Arrow + S-Arrow：参考 https://roife.github.io/posts/tapl-16/

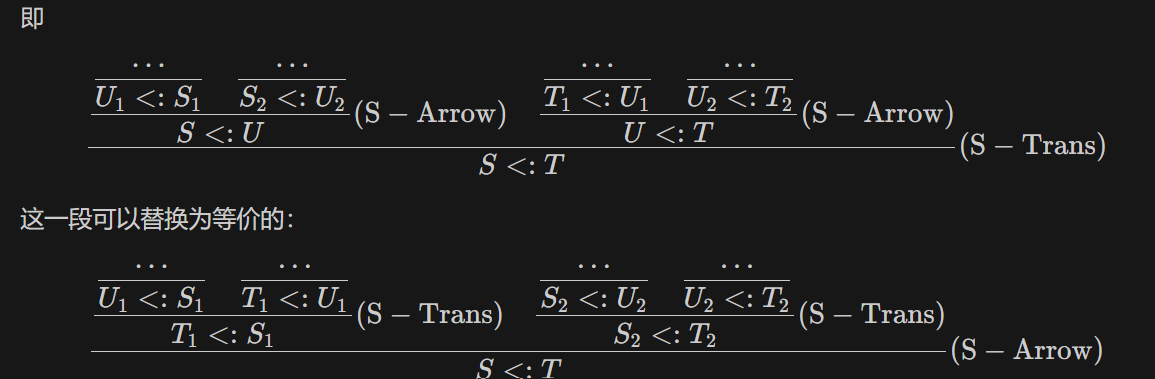
其余的情况类似。

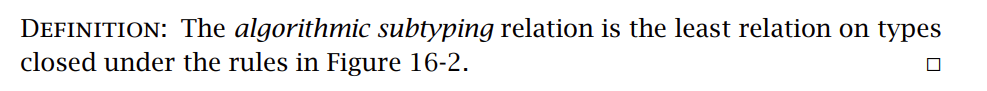
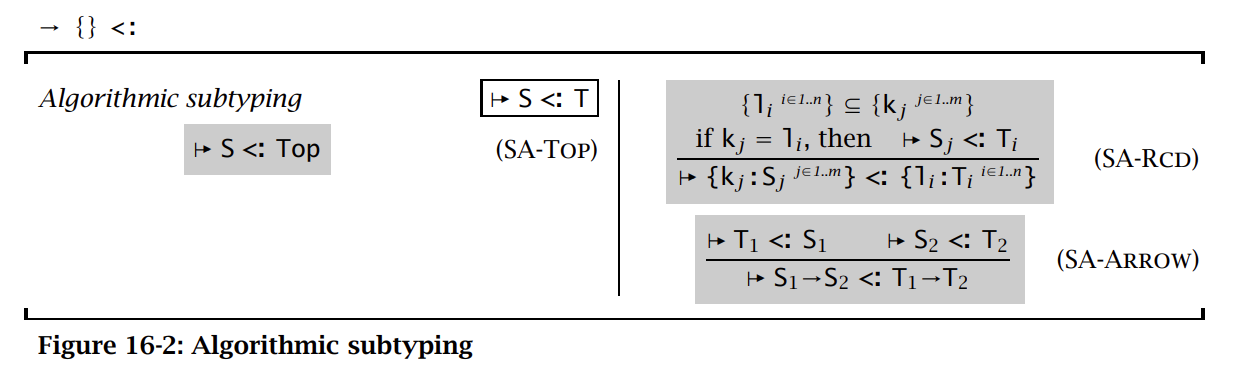
算法子类型规则和原先的子类型规则是等价的。

通过上面的算法子类型规则，可以构造出一个子类型检查算法：

这个算法是可判定的。

前面一半可以从“算法子类型规则和原先的子类型规则是等价的”验证；至于后面一半，可以从算法中观察到，函数的参数规模在逐渐减小，因此不可能存在无限调用序列。

上面的工作消除了 S-REFL 和 S-TRANS，类型关系中 T-SUB 的处理也很麻烦，也需要以同样的方式把类型关系变成语法驱动的。和消除 S-TRANS 的思路类似，在消除 S-TRANS 规则的时候，我们把 S-TRANS 在推导树的位置往上提升，直到基类型 base types。T-SUB 的位置可以在推导树上下推，比如：

• T-SUB + T-ABS：

• T-SUB + T-APP：

T-SUB 出现在左部子推导：

根据上面的算法子类型关系，\(S_{11} \rightarrow S_{12} <: T_{11} \rightarrow T_{12}\) 的上一条推导规则不会是 S-REFL 或者 S_TRANS，只能是 S-ARROW：

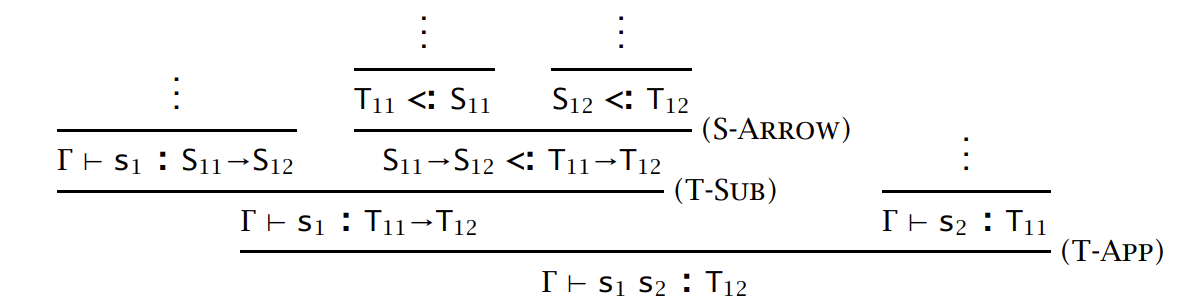
改写得到：

T-SUB 出现在右部子推导：

• T-SUB + T-SUB：

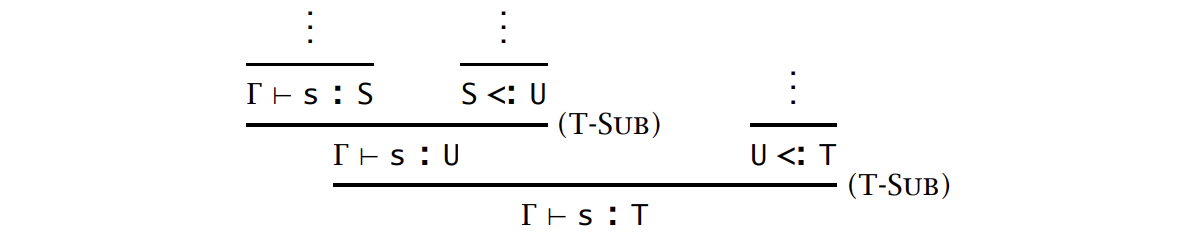
可以把任意的类型推导重写为：T-SUB 出现在 T-APP 的右子推导的末尾，或者在整个推导的末尾。如果简单删除整个推导末尾的 T-SUB 并不会有什么影响，反而使得项 \(t\) 得到了一个最小的类型，这样就只剩下 T-APP 处的 T-SUB 了，那么可以用一个新的函数应用的项上的类型规则取代 T-SUB：

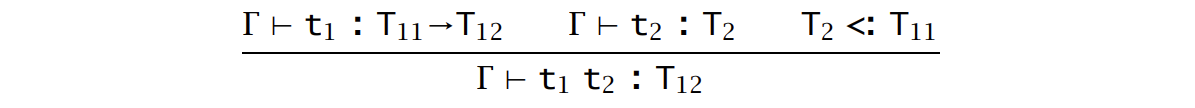
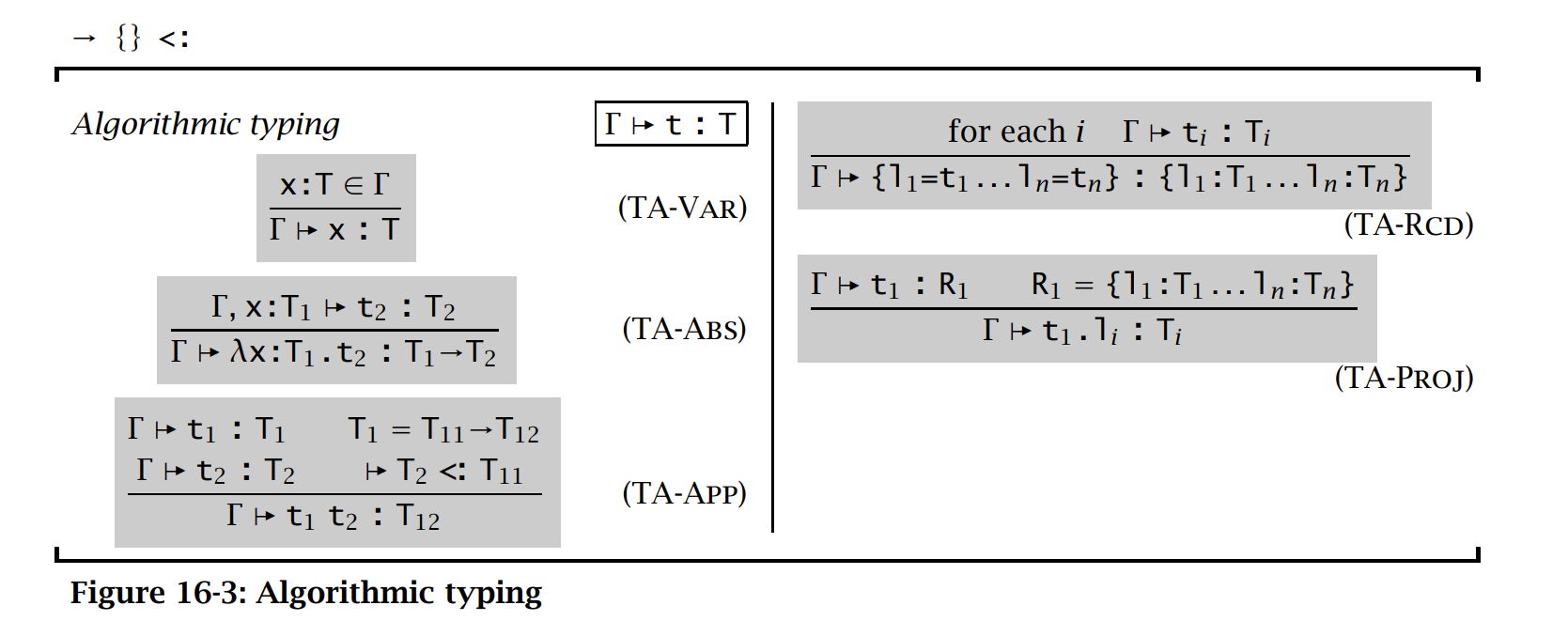
同样地，算法类型关系是 sound 和 complete 的。

对于具有多个结果分支的表达式需要有一些额外的机制，比如对于算术表达式 if：

因为要求这个 if 表达式具有一致的类型，因为要求两个分支的最小公共超类型，即 \(\{x: Bool\}\)，这称为两个类型的 join：

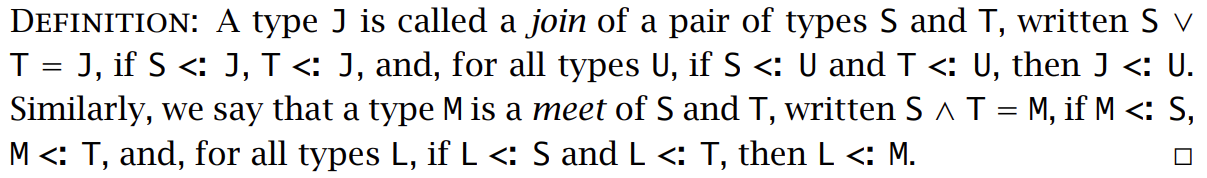
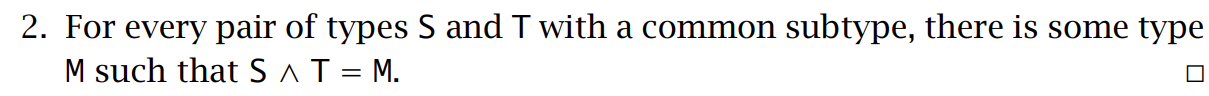
引入 Bot 类型需要对算法类型关系做一点扩展：