15 - Subtyping
(因为最近在搓类型系统,发现 tapl 也就学了个皮毛,再回来补充一下知识)
Subtyping 关系满足:自反性,传递性

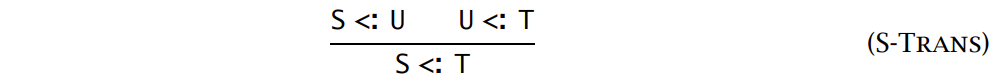
对于 record 类型有宽度和深度两个规则:


宽度对应的子类型关系有点难以理解,具备更多的 field 的 record 反而是“更小”的子类型。但是从类型对应的值集来看,更多的约束意味着更少的取值。从这个角度去理解更加准确。
对于函数类型,满足:

注意参数类型是逆变的 contravariant,返回值的类型是协变的 covariant。从代码安全的角度来看,函数 f2 是函数 f1 的子类型 f2 <: f1,意味着可以在任意的代码上下文中把 f1 替换成 f2 而不影响程序的良好行为,这要求 f2 能够处理比 f1 更多的参数 f1.p <: f2.p,返回更少可能的返回值 f2.r <: f1.r。
再引入一个 Top 类型:


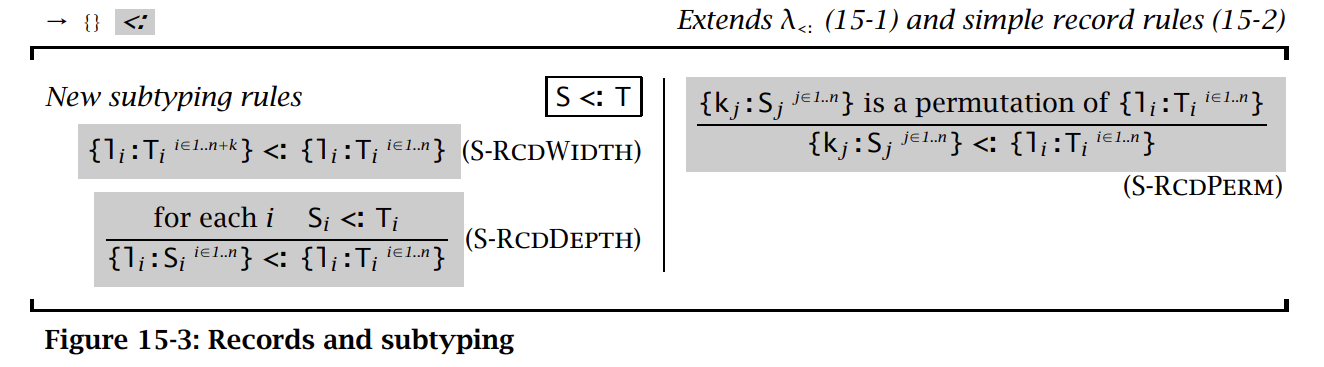
由于存在规则 S-RCDPERM,反身性不成立,所以并不能说成一个偏序关系
练习:
不好,或许可以是 \(T_1 \times T_2 <: T1 \times Top\)?
从上述规则可以引申出若干逆引理

证明 1. :
考虑对 \(S <: T_1 \rightarrow T_2\) 的推导步骤做归纳,考虑最后一条规则:
-
S-REPL,那么 \(S = T_1 \rightarrow T_2\)
-
S-TRANS,那么 \(S <: U, \ U <: T_1 \rightarrow T_2\),那么递归地讨论 \(U\) 可以得到 \(U = U_1 \rightarrow U_2\),继续对 \(S\) 做递归
-
S-ARROW,显然成立
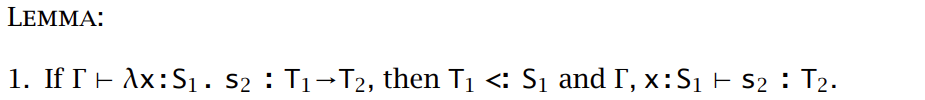
使用和上面一致的结构归纳:
-
S-REPL then T-SUB, 那么 \(S_1 = T_1, s_2 : T_2\) (根据 T-ABS 的逆引理)
-
S-TRANS 和 S-ARROW 略去


上述三个引理是为了证明类型的保持 preservation
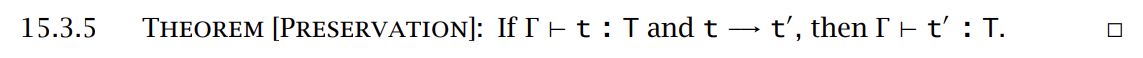

进展:
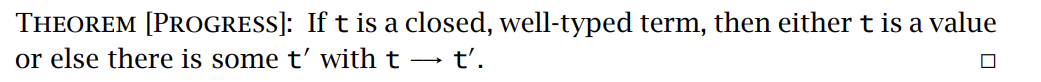
综上所述,添加了上述子类型规则的类型系统 \(\lambda_{<:}\) 仍然是类型安全的
Top 并不是包含子类型的简单类型 lambda 演算的必需部分(上面的证明完全没有涉及到 Top),但是 Top 一方面在 OOP 中被经常使用,另一方面是解决参数多态性(\(SystemF_{<:}\))中某些问题的有效工具。
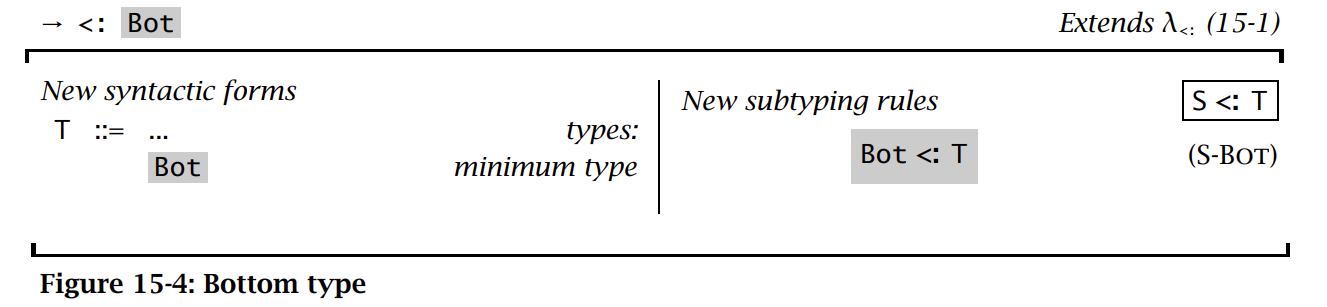
Bot 是空的 empty,意味着它对应着一个空的值集。Bot 提供了一种非常方便的方式来表达并不会返回任何值这种操作(比如抛出一个异常)。但是 Bot 的存在会增加类型系统的复杂性,一个 closed 的项 \(t_1t_2\) 可能也具有 Bot 类型。
Subtyping 还会被扩展到其他的一些特性(在之前的 tapl 章节已经出现过):
Ascription:在 Java 或 C++ 等语言中,ascription 被用作 casting,写作 (T) t。由于 subtyping 的引入,ascribe 可以被分为 up-cast 和 down-cast 两种类型,表示程序员告诉编译器应该从什么视角去观察某个项。当然,类型检查器会验证这些 ascription。Down-cast 在 OOP 语言中很有用。对于 Java 来说,down-cast 可以实现一种简陋的多态,List 可以被实现为 Top 类型的 Object List;在反射特性中,可以把从文件读取的 class 做具体化,
Variants:variants 的类型规则和 records 的很相似。不过 variants 的成员越多类型越大,records 则相反。
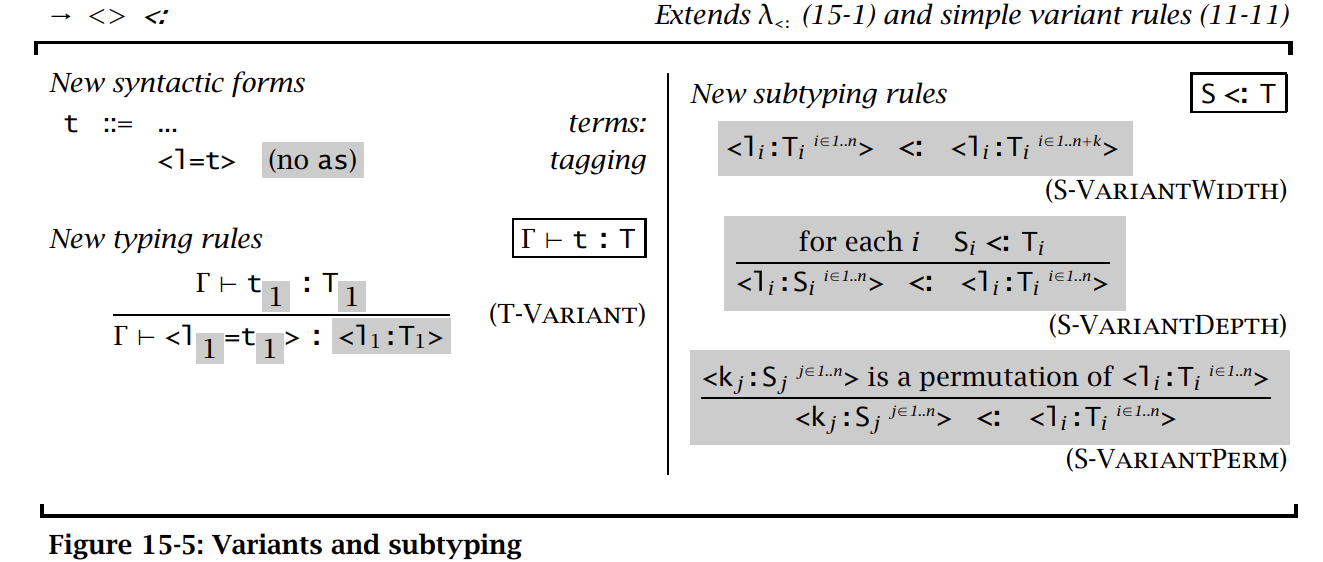
Lists 、Refs 和 Arrays:
Lists 是协变的。Ref 则是不变的,这是因为 ref 可以以两种方式被使用:读取和写入。当读取时,上下文给出的类型是 \(T_1\),如果实际的类型是 \(S_1\),那么只有 \(S_1 <: T_1\) 才是安全的;写入时则相反。用 <: 意味着可以调整 ref 保存的 record 的字段顺序,并不是严格意义上的结构相等。Array 同理。



但是 Java 允许 Array 是协变的:

这个是由于类型系统中缺乏参数化多态的问题而引入的,现在被认为是一个缺陷。
类型的交和类型的并(或者说交类型和并类型):\(T_1 \land T_2\) 包含那些既属于类型 \(T_1\) 或者类型 \(T_2\) 的值。在具有 subtyping 和 intersection type 的简单类型 lambda 演算中,一个项是可类型化的当且仅当其求值过程能够终止,这意味着对于这个类型系统,类型推理(或者说类型重建)等同于停机问题,是不可判定的。并类型则是 \(T_1\) 和 \(T_2\) 对应的值集的普通并集。

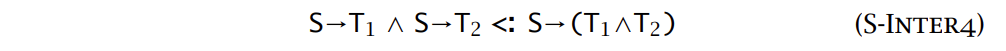



 浙公网安备 33010602011771号
浙公网安备 33010602011771号