编译原理复习笔记
文法和语言的形式定义
终结符号 \(V_T\)、非终结符号 \(V_N\) 满足 \(V_T \cap V_N = \emptyset\)
产生式 $\alpha \rightarrow \beta $, \(\alpha \in (V_T \cup V_N)^+, \beta \in (V_T \cap V_N)^*\)
文法 \(G[S] = (V_N, V_T, P, S)\),\(P\) 是产生式的集合,\(S\) 是开始符号
-
0 型文法(短语结构文法) $\alpha \rightarrow \beta $, \(\alpha \in (V_T \cup V_N)^+, \beta \in (V_T \cap V_N)^*\)
-
1 型文法(上下文有关文法)$\alpha \rightarrow \beta $, \(\alpha \in (V_T \cup V_N)^+, \beta \in (V_T \cap V_N)^*, 1 \leq |\alpha| \leq |\beta|\)
-
2 型文法(上下文无关文法)$\alpha \rightarrow \beta $, \(\alpha \in V_N, \beta \in (V_T \cap V_N)^*, 1 \leq |\alpha| \leq |\beta|\)
-
3 型文法(正则文法)满足右线性(非终结符号只能出现在产生式的最右侧)或者左线性,即 \(A \rightarrow a | aB\) 或者 \(A \rightarrow a | Ba\)
一个只含有加法、乘法和括号的文法:
\(G[E] = (\{E, T, F\}, \{i, +, *, (, ) \}, P, E)\)
\(P = \{E \rightarrow E + T | T, T \rightarrow T * F | F, F \rightarrow (E) | i \}\)
推导的符号暂时定义为 \(\Rightarrow\)
句型:如果 \(G[E]\) 满足 \(E \Rightarrow^* u\),那么 \(u\) 就是文法 \(G[E]\) 的一个句型
句子:如果 \(G[E]\) 满足 \(E \Rightarrow^* u\) 并且 \(u \in V_T^*\),那么 \(u\) 就是文法 \(G[E]\) 的一个句子
浅显的理解,句型等于所有在推导中可能出现的串,句子等于所有推导最后一步的串
语言:文法 \(G[E]\) 的语言是所有句子的集合,在描述时可以写成 \(V_T^*\) 的形式
语法树:满足下面条件的树
-
每个结点都用一个标记 \(l\) 表示,\(l \in V_N \cup V_T\)
-
树根的标记是起始符号
-
非叶子节点的标记必然是非终结符号
-
父子关系必然和一条产生式规则相对应
最左(右)推导:如果在某个推导过程中的任何一步直接推导αβ中,都是对符号串α的最左(右)非终结符号进行替换,则称其为最左(右)推导
如果产生式满足 \(U \rightarrow xUy\),那么为规则递归(直接递归)
如果产生式满足 \(U \Rightarrow^* xUy\),那么为间接递归,同样地,可以定义左右递归
如果两个文法产生的语言是相同的,则称这两个文法是等价文法
结合性体现在文法是左递归还是右递归,优先级则体现在出现在语法树的位置
如果文法\(G\)的某个句子存在两棵(包括两棵)以上不同的语法树(即有两个不同的最左/最右推导),则称该文法是二义性文法
二义性问题是不可判定的
正向标记法可以推导出所有可达的非终结符号,反向标记法可以推导出所有可推导出终结符号串的非终结符号
有穷自动机
正则文法、正则表达式、有穷自动机相互等价
确定型有穷自动机 \(\text{DFA} = \{Q, \Sigma, t, q_0, F \}\), $t: Q \times \Sigma \rightarrow Q $
非确定型有穷自动机 \(\text{NFA} = \{Q, \Sigma, t, Q_0, F \}\), \(t: Q \times \Sigma^* \rightarrow 2^Q\)
被一个有穷自动机接受的符号串的集合称为这个自动机的语言 \(L(\text{DFA})\)
如果两个有穷自动机 \(A_1, A_2\) 满足 \(L(A_1) = L(A_2)\),那么它们是等价的
DFA 和 NFA 在表达能力上是等价的:
-
\(\text{DFA} \Rightarrow \text{NFA}\):DFA 天然的是一种 NFA,显然成立
-
\(\text{NFA} \Rightarrow \text{DFA}\):
TBD
从证明过程中容易得出 NFA 向 DFA 转换的方法:
定义 \(\epsilon\) 闭包:\(p' \in \epsilon -Closure(p)\) 当且仅当 \(p\) 通过若干条 \(\epsilon\) 的转移边后可以到达 \(p'\)
通过 \(\epsilon\) 闭包,可以把转移函数 \(t\) 改写成 \(t: 2^Q \times \Sigma \rightarrow 2^Q\),并且只在必要的时刻引入状态的集合
这样构造出的 DFA 可以化简。对于两个状态集合 \(P, Q\),如果对于任意的符号 \(k \in \Sigma\),都有 \(t(P, \Sigma) = t(Q, \Sigma) = R\),那么它们可以合并;换言之,如果两个状态到达了不同的子集中,那么它们就应该从一个状态集合中分离。
通过正则文法可以构造出一个DFA,使得二者能接受的符号串集合相同。同理,通过DFA可以构造出一个正则文法。
对于 \(U \rightarrow aW\),可以构造状态及其转移边 U --a--> W;对于 \(U \rightarrow Wa\),可以构造 W --a--> U,反之亦然。
通过正则表达式也可以构造出一个等价的DFA。正则表达式有递归定义:\((e), e_1e_2, e_1|e_2, e^*\)。通过正则表达式直接构造DFA比较麻烦,可以先构造出对应的GNFA在转换为等价DFA。
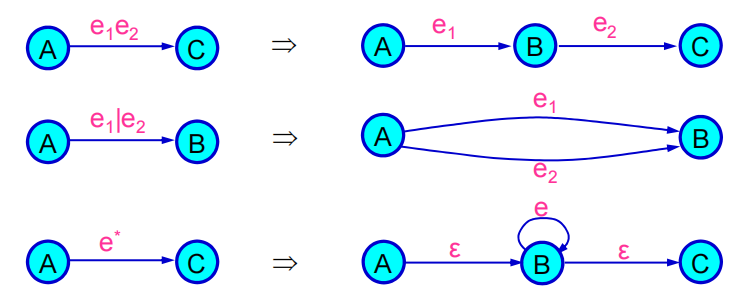
通过DFA构造出对应的正则表达式需要不断地删去状态。可以以一个最小状态机为例。TBD。
递归下降语法分析
构建一个语法分析器最方便的方法是递归下降。

自上而下语法分析
递归下降会遇到两个问题:
-
公共前缀:这需要预处理文法,提取不同的分支之间的公共前缀。
-
左递归导致的无穷递归:因为一般写出的递归下降方法是前序遍历的,我们会先处理左子树,如果有个左递归我们会不断进入左子树,不会接受任何的新字符。
公共前缀的处理比较简单,左递归难处理一些:
-
直接左递归:对于产生式 \(A \rightarrow A\alpha_1|A\alpha_2|...|\beta_1|\beta_2\),引入新的符号 \(A'\) 使得串变为 \(A \rightarrow \beta_1A'|\beta_2A'|...\) \(A' \rightarrow \alpha_1A' | ...\),容易证明它们等价
-
间接左递归:通过代换把间接左递归转换为直接左递归的形式
递归下降的其他问题是:
-
不断回溯效率太低
-
代码本身和文法深度耦合(虽然你可以构建一个通过文法自动构建解析程序的程序)
因此我们引入两个新的集合防止我们做出错误的抉择:
\(\text{FIRST}\) 集合:\(FIRST(A)\) 表示符号 \(A\) 可以推导出的所有串的首部终结符号的集合,这决定了通过某个符号我们进入哪一个解析程序
\(\text{FOLLOW}\) 集合:\(FOLLOW(A)\) 表示文法的所有句型中,可能紧跟着非终结符号 \(A\) 的所有终结符号的集合,这决定了我们是否结束当前的解析程序进入下一个解析程序
想法是好的,但是大家发现容易执行坏了:
-
如果一个产生式的多个右部的 \(FIRST\) 集合相交,且无法通过提取公共前缀的方式解决,那么我们还是会进入错误的解析程序
-
如果对于 \(U \rightarrow \alpha | \epsilon\),\(FOLLOW(U)\) 和 \(FIRST(\alpha)\) 相交,那么我们就不知道是进入新的解析程序还是退出(大家给它起了个名字叫移入归约冲突)
因此,不满足上面两个条件的文法被称为 LL(1) 文法,可以使用这两个集合改进解析方法
下面需要给这两个“想法”下形式化定义:




后面又引入了一个集合 \(SELECT\) 用来统一判断某个文法是否是 LL(1) 的,此外 \(SELECT\) 的元素还是一种“程序接下来要做什么”的标识

下面需要把上面的形式化想法转化为实践,考虑利用它们构建一个 LL(1) 分析算法。我们引入一个分析表把集合转化成状态与对应的动作,再引入符号栈和状态栈保存状态(下推自动机):

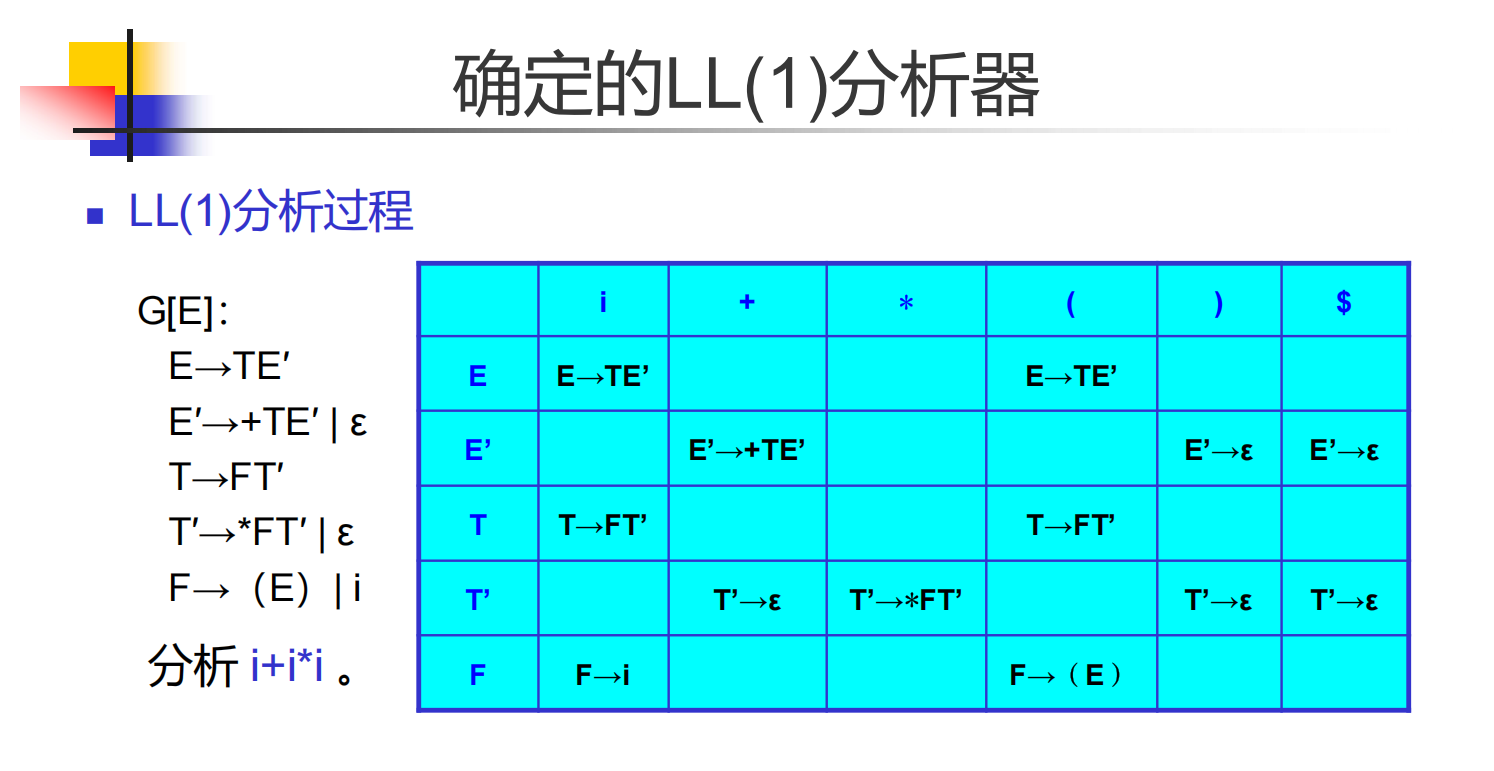
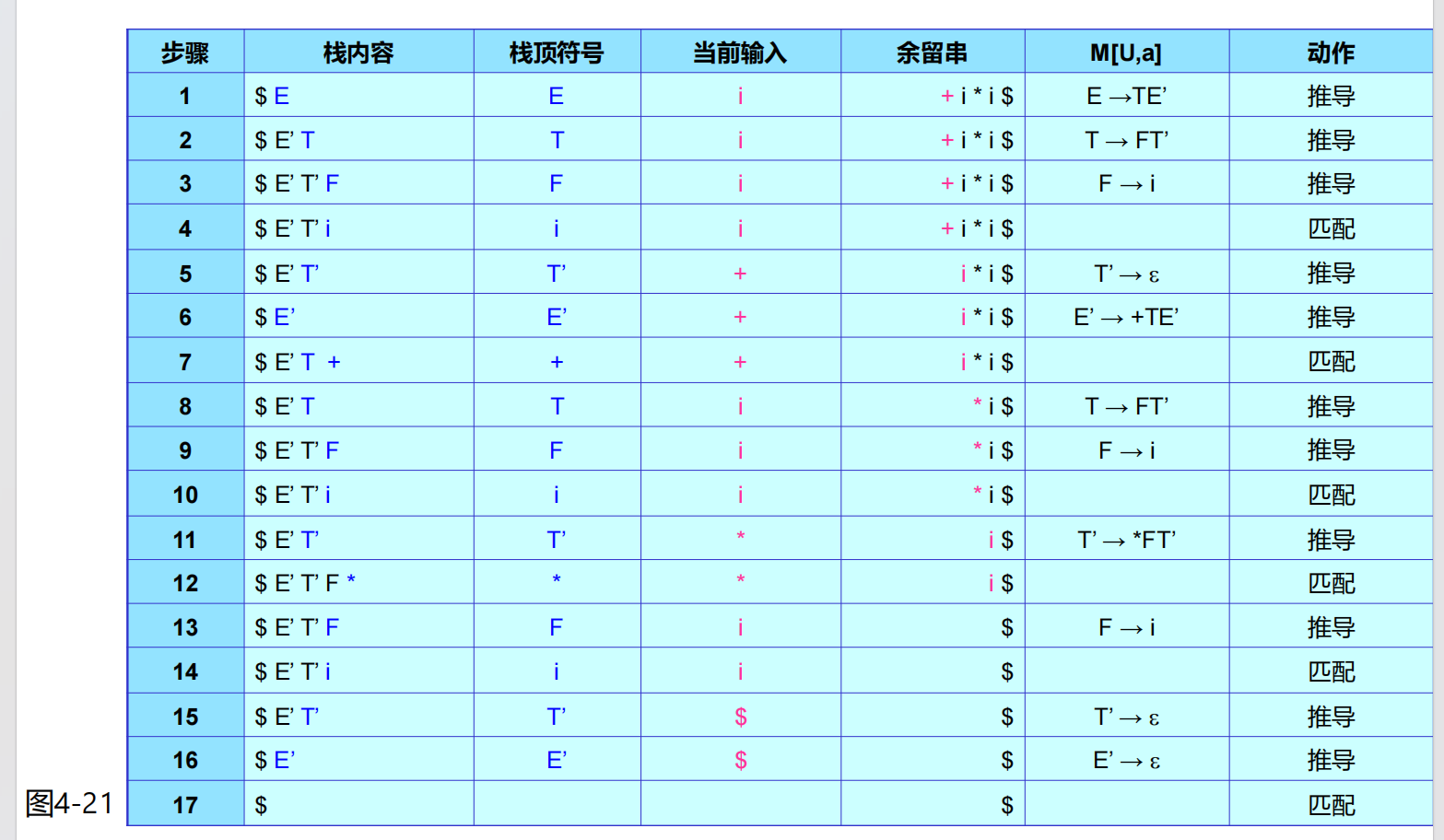
自下而上语法分析
相比于自上而下的语法分析,自下而上的语法分析不发源于递归下降的想法,而是自下而上的构建语法树,不过一样面临“选择”问题。选择什么时候移入或归约。
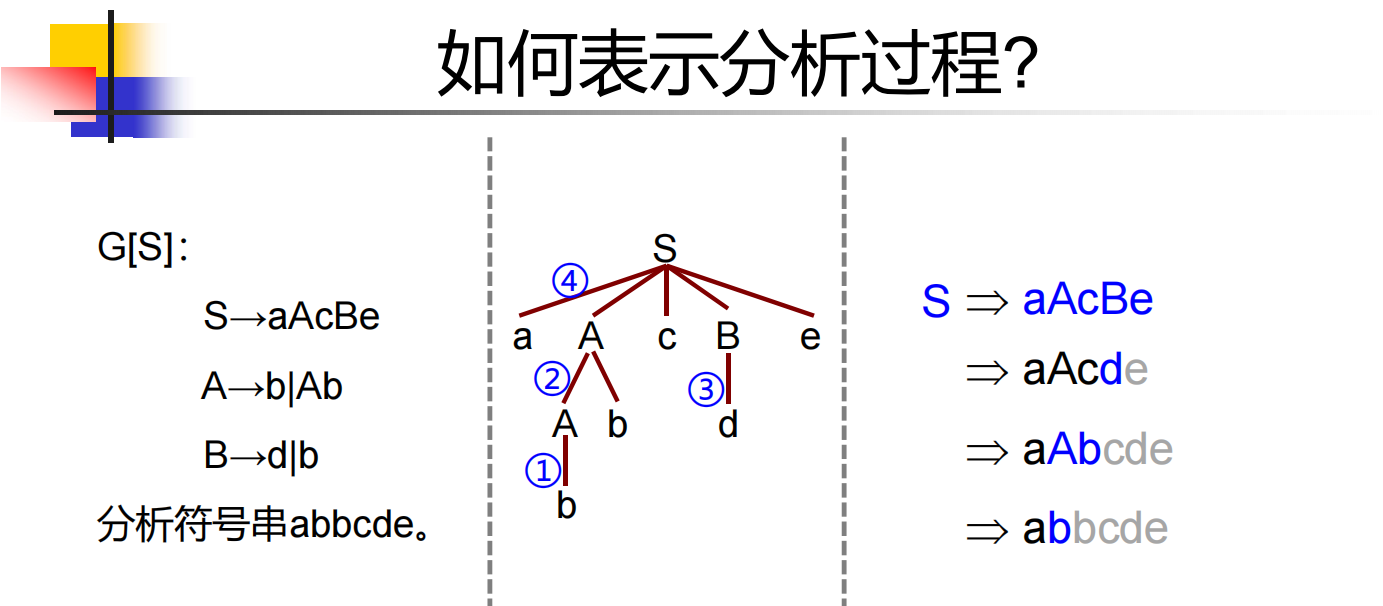
首先给出几个定义:
-
短语:对于文法 \(G[E]\)和它的一个句型 \(xuy\),如果有 \(E \rightarrow xUy\) 满足 \(U \Rightarrow^* u\),那么 \(u\) 就是一个短语。直观的说,短语代表了那些能被规约的东西。
-
直接短语:对于文法 \(G[E]\)和它的一个句型 \(xuy\),如果有 \(E \rightarrow xUy\) 满足 \(U \Rightarrow u\),那么 \(u\) 就是一个短语。直观的说,短语代表了那些直接一步规约的东西。
-
句柄:句型的最左直接短语称为句柄
从定义不难看出,不断地对某个句型的句柄进行一次归约,那么最终能归约到开始符号
对于任意一个长度为 \(k\) 的句柄,它必须经历 \(k\) 次移入和 \(1\) 次归约,如果用一个状态机去描述的话,一共有 \(k + 1\) 个状态
又因为句柄是最左直接短语,不难看出某个句柄必然对应一个产生式的右部,产生式的数量和长度都是有限的,那么所有状态的数量也是有限的。我们用一种记号描述状态:

所有的这种被描述的状态称为 LR(0) 项(term)
显然,只利用这些状态以及状态之间的转移关系只能构建出一个 DFA,不能构建出一个 PDA,也无法进行语法分析。因此同样地需要引入栈。这里还有一个常考的定义:
活前缀:活前缀包含了句柄识别到当前时刻的历史,并逐步向后传递,最长的活前缀(可归约前缀)包含了句柄完全被识别的整个历史。
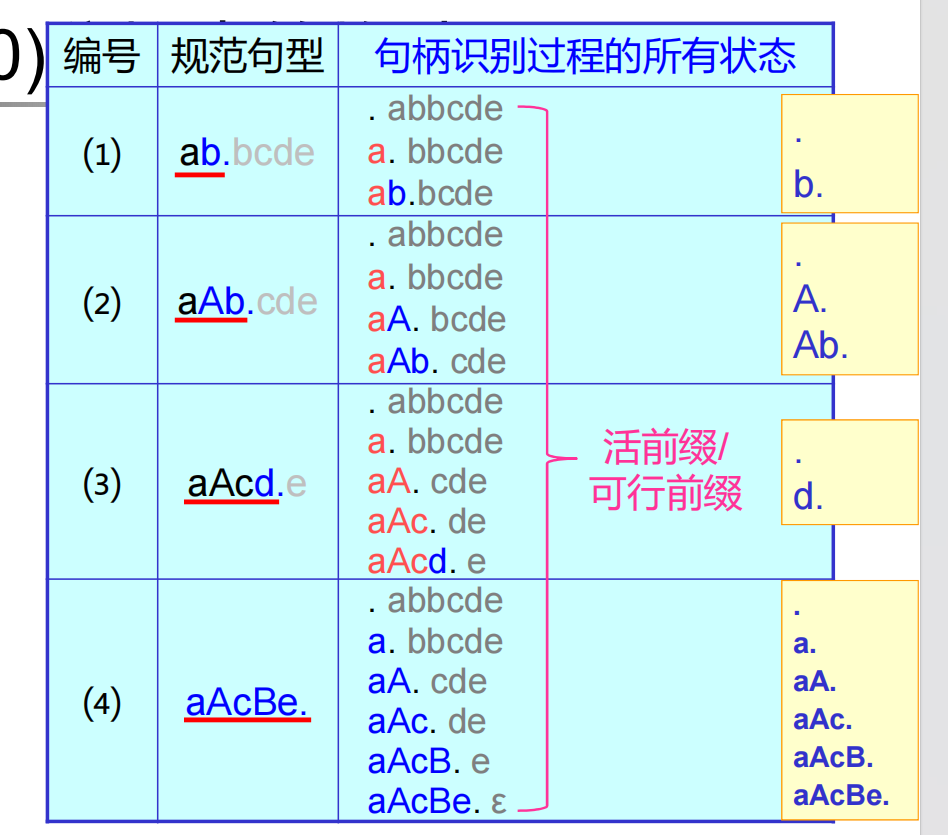
说人话,活前缀就是分析栈中可能出现的所有串

如果把每个 LR(0) 项都建成一个状态,不仅内存的开销很大,还因为有 \(\epsilon\) 边的存在导致这实际上是一个 NFA,因此使用一个 \(\epsilon -CLOSURE\) 来合并 NFA 中的一些结点。

哎写不动了


SLR 在 LR(0) 上做了一点小改进,避免了一些错误的归约状态(从而避免掉一些移入-归约冲突)

LR(1) 在 SLR 上做了更好的改进,通过在状态中引入一个符号,标识了在某些情况下的紧跟的终结符,增强了表达能力(可以理解成本来很泛泛的一个状态添加了一个细节),规避掉了更多的归约归约冲突

LALR(1) 只是对 LR(1) 在存储空间上的改进
语法制导翻译
从理论上也不是很漂亮,从实践上也不是很实用
可以为文法符号,引入一组属性 \(attr_1, attr_2, ...\),并定义程序的语义 \([[P]] = f(attr)\),在这个过程中,随着语法分析进行,每当使用一个产生式的时候就执行对应的语义动作
注释语法树:语法分析树的各个节点上标记了相应的属性值
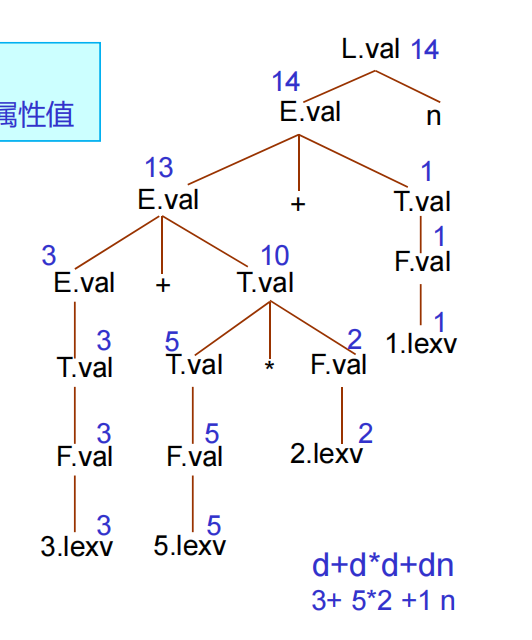
语法制导定义 SDD:定义与文法符号相关联的属性集,定义与产生式关联的一组语义规则(程序片段),属性文法是没有副作用的 SDD
语法指导翻译方案:将程序片段附加到文法各个产生式右部的合适位置,后缀SDT指所有程序片段都在产生式的最后进行
属性本身可以被划分为综合属性和继承属性:
综合属性:从子结点的属性值计算得出的属性
继承属性:从父结点或兄弟结点继承的属性值
中间代码生成的核心在于处理文法、程序、中间代码三种不同的顺序关系。回填技术是处理这个问题的一个很好的算法。
怎么中间代码不讲 SSA 啊(
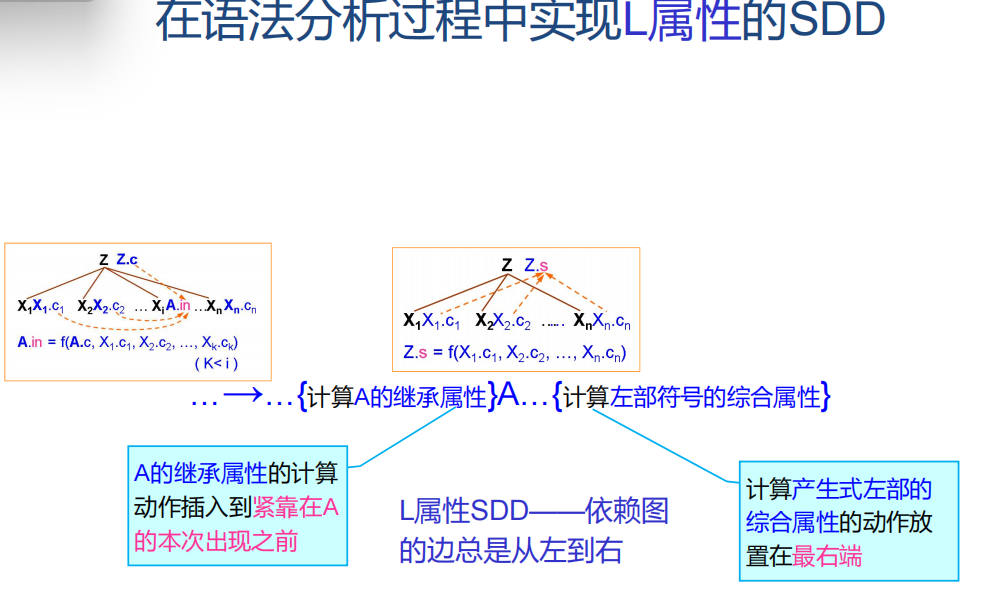
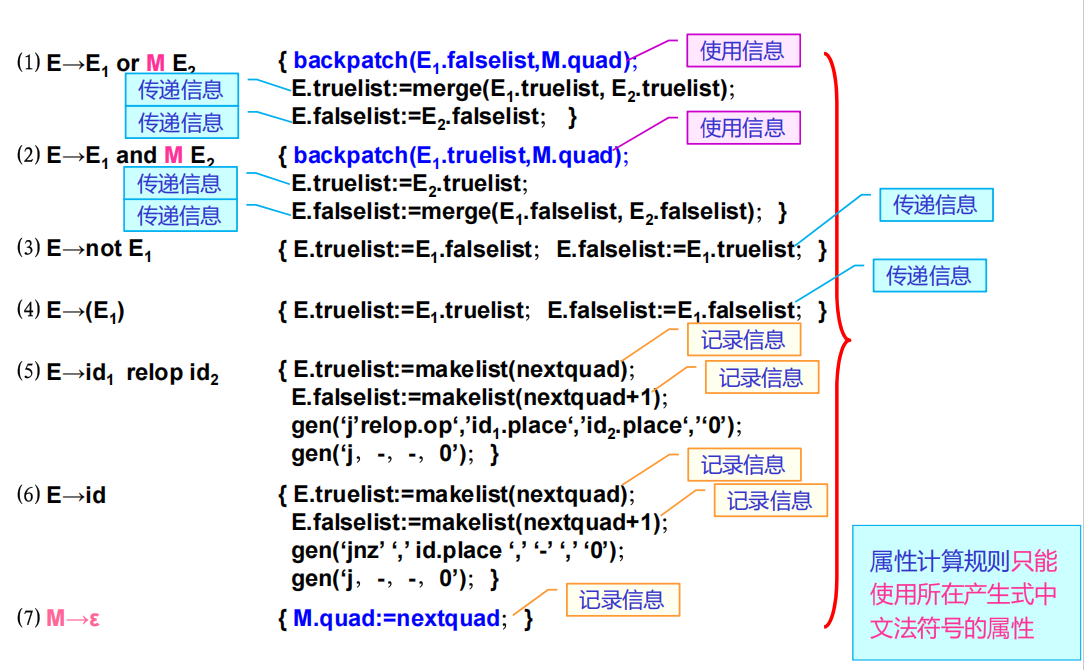
在涉及控制流语句的时候,我们会定义两个链表 falselist 和 truelist,用来保存所有涉及跳转的语句的真出口和假出口,这样在回填时就无需再次向下遍历整个语法树,通过链表中的位置就可以访问所有需要回填的位置
运行时刻环境
最近嵌套作用域原则:一个 Identifier 的作用域是个包含了这个 Identifier 的说明的最近的过程或函数
参数传递规则:
-
传地址:callee 接受到的是一个引用
-
传值:calle 接受到的是值本身
-
传结果:哎这个好抽象 被调用者的代码中使用形式参数时,访问的是形式参数的值单元,不修改实在参数;在结束调用返回时,修改实在参数
-
传名:常见在数组传递中 个人觉得和传地址区别不大 被调用者数据区中需要一个单元存放实参地址计算程序的入口地址
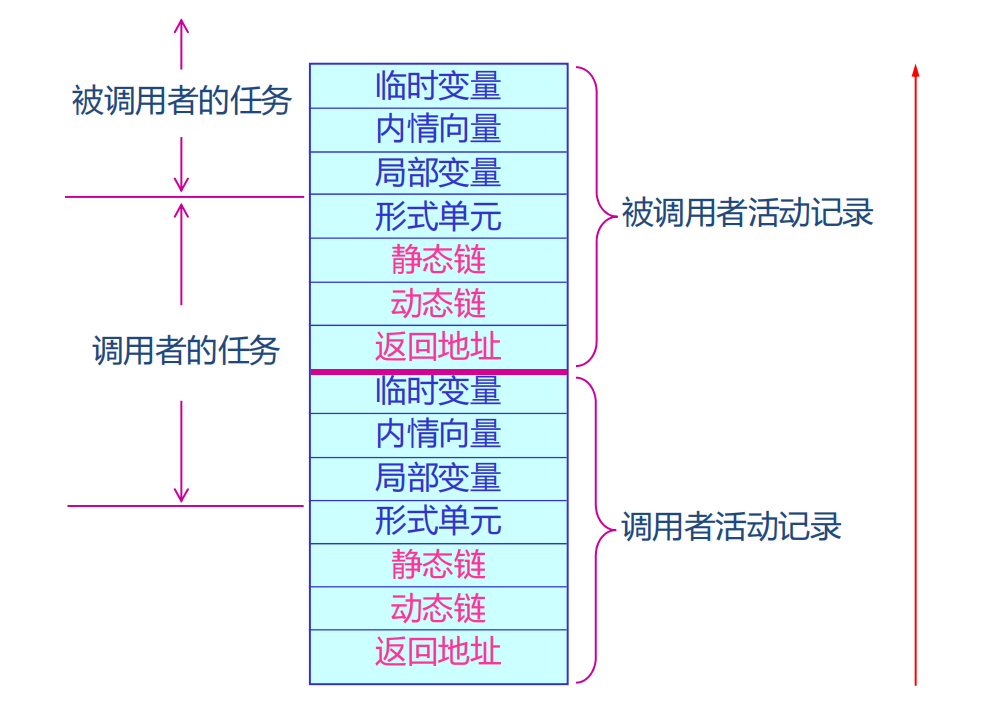
一个过程的数据区(也叫活动记录)是一个在执行中会使用的连续数据块,几乎所有数据区的大小都可以在编译期确定。这意味着在生成代码时,可以确定申请多少的栈区大小,从而组织整个存储空间。
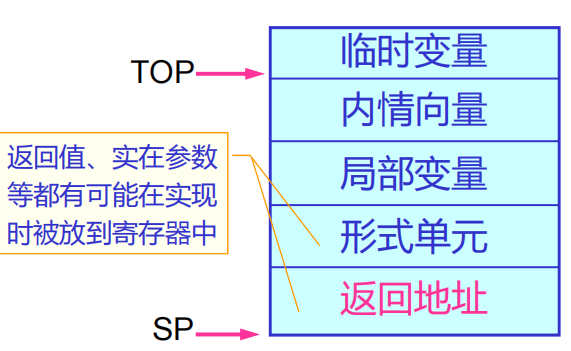
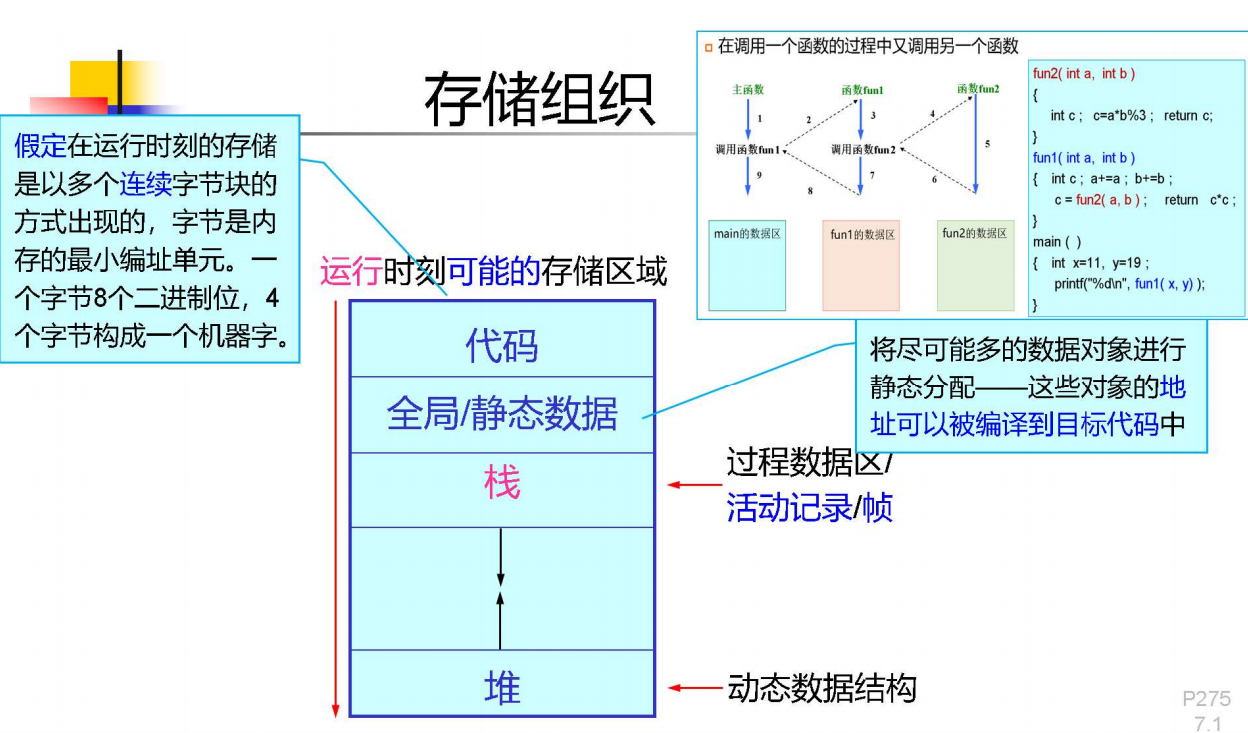
我们假定栈向高地址增长。

写在考试前的总结
自动机理论与形式文法
-
注意辨别自己构建的是 NFA 还是 DFA
-
假设 DFA D 识别语言 L,如果要构造一个新的 DFA D' 识别语言 L 的补集,那么 D' 就是把 D 的接受状态和非接受状态翻转
-
在化简某个 DFA 时,先观察是否能划分为接受状态集和非接受状态集,如果能,那么不断地分割就可以得到最简 DFA,否则肉眼观察划分吧
-
题目中出现的 DFA 与正则表达式的对应,关注“连续的...”“以...为结尾”“以...开头”这样的特征
-
题目中可能出现不止一个左递归
-
对于 E -> E E | a 这种形式的文法,很容易构造其无二义性版本:E -> a E
-
一个包含加法和乘法的文法:
Expr -> Expr + Term | Term
Term -> Term * Factor | Factor
Factor -> (Expr) | id
可以通过消除左递归的方式得到它的另一个版本:
Expr -> Term Expr'
Expr' -> + Term Expr' | epsilon
Term -> Factor Term'
Term' -> * Factor Term' | epsilon
Factor -> (Expr) | id
这两个版本都很常用而且在龙书上出现过
自上而下的语法分析
- 自上而下的语法分析发源于递归下降法,First 集和 Follow 集的发明可以节省递归下降法在某些情况下的非必要搜索回溯步骤:
比如
E -> A B C
A -> a | epsilon
B -> b | epsilon
C -> c | epsilon
input: bc
对于输入串 bc,如果没有 First 集辅助选择,递归下降法就会错误的进入 A 对应的子程序,效率很低
为了更方便,大家干脆把所有的子程序进入的逻辑全都提取出来,搞成一张表,变成表格驱动的语法分析,用原输入串上的一个移动的指针代表分析进度
First 集合之间的冲突可以通过提取公共前缀解决,First 集合和 Follow 集合之间的冲突则需要谨慎文法设计
- LL(1) 分析表的构建:
-
对于产生式 A -> a, 如果终结符 s 在 FIRST(a) 中,那么在表中的对应位置填入这个产生式
-
对于产生式 A -> a, 如果 epsilon 在 FIRST(a) 中,那么对于 FOLLOW(a) 中的每个终结符,把产生式加入到它们对应的位置中
- LL(1) 算法的执行:
三个部分,符号栈、输入串、动作,符号栈的栈底放在右边更合适,动作包括“推导”和“匹配”
自下而上的语法分析
-
自下而上的语法分析来源于对句柄的认识,以及某个句柄必然出现在符号栈的顶端的这一推论
-
LR 比 LL 更加强大
-
内核项:初始项以及点不在最左端的所有项
-
SLR 分析表的构建:
-
如果状态 A 通过一个终结符号 s 达到状态 B,那么在表中 ACTION 的对应位置填写移入 s,如果状态 A 通过一个非终结符号 E 到达状态 B,在么在表中 GOTO 的对应位置填写 B
-
如果状态 A 里面有产生式 E -> e · 已经终结,那么对于 FOLLOW(E) 中的所有终结符号 s,在对应位置填写归约
-
如果 S' -> S · 在状态中,那么 $ 置为 acc
- LR(1) 项目集的构建:
-
从 S' -> S · , $ 开始,对于每个 A -> a · Bc, y,把 B -> · b, FIRST(cy) 加入状态中
-
转移边不改变后面跟的符号
-
LR(1) 分析表的构建:把 FOLLOW(E) 改编成后面跟的符号,后面跟的符号对移入动作没有贡献
-
LALR 分析表的构建:在 LR(1) 项目集的基础上,合并掉那些具有相同核心的集合,在分析表中体现为合并掉两个状态行
-
LR 语法分析算法的执行:
四个部分,状态栈,符号栈,输入串,动作,当执行一个归约动作时,符号栈和状态栈要弹出相同数量的元素,符号栈压入被归约的符号,状态栈则压入栈顶符号 GOTO 后的结果



 浙公网安备 33010602011771号
浙公网安备 33010602011771号