数据流分析方法基础

南京大学《软件分析》学习笔记 1

课太好了，忍不住写篇博客从头推导一下

理论

偏序集 poset

偏序关系 偏序关系是满足下面三个条件的二元关系：

• 自反性

• 反对称性

• 传递性

偏序集 poset 偏序集定义为一个集合以及集合上的偏序关系，表示为 \((P, \sqsubseteq)\)

上界 upper bound 和下界 lower bound 给定一个偏序集 \((P, \sqsubseteq)\)，那么对于一个子集 \(S \subseteq P\)，它的上界是 \(u\) 当且仅当 \(\forall x \in S\) 都满足 \(x \sqsubseteq u\)。下界的定义类似。

最小上界 lub 和最大下界 mlb 给定一个偏序集 \((P, \sqsubseteq)\)，那么对于一个子集 \(S \subseteq P\)，它的最小上界 \(\sqcup S\) 满足对于所有的上界 \(u\) 都满足 \(\sqcup S \sqsubseteq u\)。符号 \(\sqcup\) 可以叫做并 join，\(\sqcup S\) 表示并运算作用在整个集合 \(S\) 上，并也可以当成一个二元运算符用 \(a \sqcup b\) 表示集合 \({a, b}\) 的最小上界。最大下界 \(\sqcap S\) 的定义类似，符号 \(\sqcap\) 可以叫做交 meet。

• 不是每一个偏序集都有最小上界和最大下界。证明：很容易举出反例。

• 最小上界和最大下界一定是唯一的。证明：反证法假设不唯一，通过反对称性容易证伪。

格 Lattice

格 lattice （格的序理论定义）如果一个偏序集 \((P, \sqsubseteq)\) 中的 \(\forall a, b \in P\) 都满足 \(a \sqcup b\) 和 $a \sqcap b $ 存在，那么这个偏序集叫做一个格，记作 \(L = (P, \sqsubseteq)\)

半格 semilattice 如果一个偏序集 \((P, \sqsubseteq)\) 中的 \(\forall a, b \in P\) 都满足只有 \(a \sqcup b\) ，那么这个偏序集叫做一个并半格。

完全格 complete lattice 如果一个偏序集 \((P, \sqsubseteq)\) 的任意一个子集 \(S\) 都满足最小上界和最大下界都存在，那么这个偏序集是一个完全格。在完全格中 \(P\) 的最小上界和最大下界分别称为 top 和 bottom。

• 每一个有限的格都是完全格。证明：容易证明，把求一个子集的最小上界的过程拆分为多个二元运算。

• 完全格不一定都是有限的。证明：容易举出反例 \(([0, 1], \leq)\)。

格的笛卡尔积 product lattice 可以把多个格通过笛卡尔积组装成一个更大的格。

• 如果每一个格都是完全格，那么笛卡尔积也是完全格。

方法

程序一定会停止运行（达到不动点）

单调性 monotonicity 格上的某个函数 \(F : L \rightarrow L\) 具有单调性当且仅当 \(\forall x, y \in L, x \sqsubseteq y\) 满足 \(F(x) \sqsubseteq F(y)\)（数据流分析的方法大多满足 F 为单调增，下面的篇幅都假设 F 是单调增的）。

数据流分析中转移函数的单调性 现在我们要证明数据流分析中的转移函数 \(F\) 是满足单调性的。转移函数 \(F\) 有两个函数组成：meetInto 和 transferNode

首先考虑 transferNode，对于 IR 中的一个语句（对应图上的一个结点），它的 gen 集和 kill 集（use 集和 def 集）仅仅取决于语句本身，这意味着 gen 集和 kill 集是固定不变的，对于 \(OUT = gen \cup (IN - kill)\)，如果假设 \(OUT\) 是语句在格上的取值，那么它的单调性完全依赖于 \(IN\) 的变化，所以只要 meetInto 单调增，那么 transferNode 也单调增。

其次考虑 meetInto，对于 \(IN = \sqcup_{preprocessor} OUT\)，我们要证明 \(\sqcup\) 是单调的，即 $\forall x, y, z \in L, x \sqsubseteq y $ 都有 \(x \sqcup z \sqsubseteq y \sqcup z\)。\(y \sqsubseteq y \sqcup z\)，又因为 \(x \sqsubseteq y\)，所以 \(x \sqsubseteq y \sqcup z\)，所以 \(x \sqcup z \sqsubseteq y \sqcup z\)

所以整体的函数 \(F\) 是单调增的。

不动点的存在性 现在证明对于完全格 \(L\)，必然存在一个不动点满足 \(F(p) = p, p \in L\)

根据 bottom 的定义，对于格上的值 bottom（写作 \(\perp\)），对其使用 \(F: L \rightarrow L\)，那么 \(F(\perp) \in L\)，那么必然有 \(\perp \sqsubseteq F(\perp)\)。

又因为 \(F\) 具有单调性，那么 \(F(\perp) \sqsubseteq F(F(\perp))\)，那么 \(\perp \sqsubseteq F(\perp) \sqsubseteq F(F(\perp)) \sqsubseteq ... F^k(\perp)\)

根据鸽笼原理，当 \(k >= |L| + 1\) 时，必然有 \(F^i(\perp) = F^j(\perp)\)，证毕。

最小不动点 容易证明，从 bottom 逐步应用函数 \(F\) 得到的不动点一定是最小的那个不动点。

不动点定理 给定一个完备格，如果函数 \(F\) 是单调的，那么可以通过迭代\(F(\perp), F^2(\perp), ...\)直到达到一个不动点，来找到最小不动点。

程序会在有限时间内停止运行（达到不动点）

格的高度 定义格的高度为从 top 到 bottom 的最长距离

迭代时间 如果格的高度为 \(k\)，对于 \(L^n\) 迭代 \(n * k\) 次肯定可以到达不动点。

May Analysis 和 Must Analysis

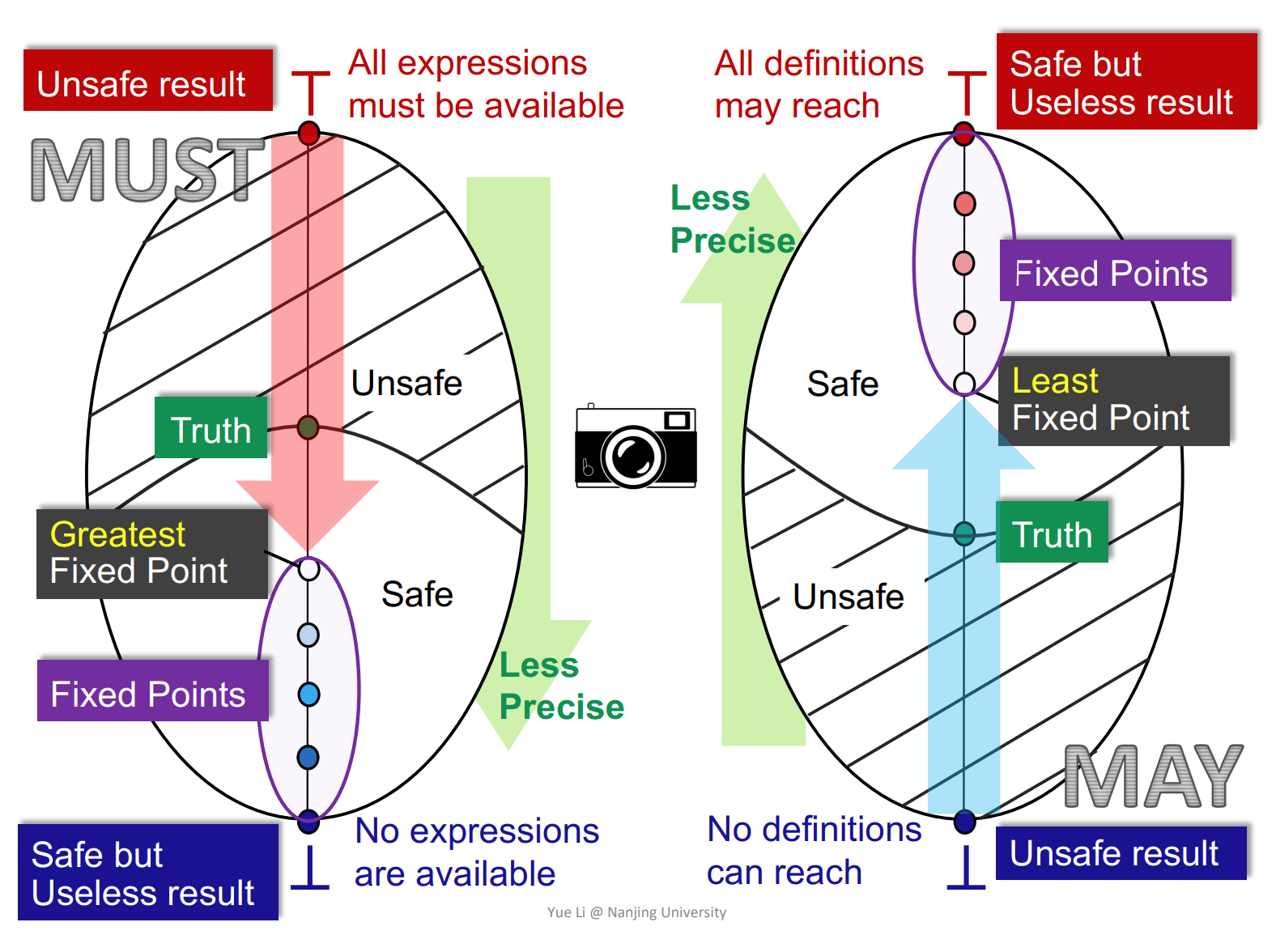
• 怎么理解这张图？

右边的图以到达定值分析方法为例，如果我们在一开始给所有的变量创造一个 var = undefined 的定值，把这个定值能否到达（0，1）作为图中结点的在格上的值域，那么所有的 var = undefined 都不能到达意味着这个程序竟然初始化了所有的变量。这对于分析程序来说是不安全的。所有的 var = undefined 都到达了意味着程序可能对于所有的变量都没有初始化，这肯定是安全的，这会让程序员去仔细检查自己的代码，但是这没啥用，体现不出分析程序的价值。

• 为什么不动点一定是 safe 的？

一个想法是这取决于转移函数 F，如果你在 F 中对于哪些不确定的情况都做出最坏的假设（对于分析来说就是最 safe 的），那么不动点必然是 safe 的。

MOP

懒得写了，不如贴图算了