6-Nameless Representation of Terms
无名称项
de Bruijn 使用自然数来表示项,而不是字母组成的名称;自然数 k 表示绑定于相对于当前层第 k 个 绑定器 binder 的囿变量(the variable bound by the k'th enclosing λ)
马世龙版《类型和程序设计语言》使用“囿”来形容这种被界定的关系
举例来说:
λx.x 表示为 λ.0
λx.λy.x (y x) 表示为 λ.λ.1 (0 1)
λm.λn.λs.λz.m s (n z s) 表示为 λ.λ.λ.λ.3 1 (2 0 1)
(λx.(λx.x)) (λx.x) 表示为 (λ.(λ.0)) (λ.0)
无名称项也称为 de Bruijn 项;用来表示项的自然数称为 Bruijn 索引,“静态距离”也表示相同的概念
定义:设 T 是最小的集簇 {T0, T1, ...} 使得:
-
当
0 <= k < n,k ∈ Tn -
如果
t1 ∈ T并且n > 0则λ.t1 ∈ Tn-1 -
如果
t1 ∈ Tn并且t2 ∈ Tn则(t1 t2) ∈ Tn
Tn 的元素为至多含有 n 个自由变量的项
命名上下文 naming context
对于所有自由变量指派 assign 一个 de Bruijn 索引(称为一个命名上下文 naming context),并且一致地使用这个指派 Γ
数值指当前这一层的索引,当进入一个新的绑定器 binder,索引需要 + 1
比如:
定义:定义 x0, ..., xn 为变量名称,命名上下文 Γ = xn, xn-1, ..., x1, x0 为所有变量指派每个 xi,且 de Bruijn 索引为 i,序列最右边的索引是 0,代表当前这一层,与我们分配 de Bruijn 项的方式相符合;用 dom(Γ) 表示变量名称的集合 {xn, ..., x0}
移位和代换 shifting and substitution
为了正确地进行代换 substitute,有时需要改变自由变量的编号,这个操作称为移位 shift
比如:
[x → s](λy.x) where s=z(λw.w)
得到结果 λy.z(λw.w)
显然, s 中的自由变量 z 深度加深了一层,如果只单纯替换 z 在最外层的命名上下文,就忽略了绑定器的 + 1 影响
移位的本质是对绑定器产生的影响的弥补
对于上面提到的例子:
假设 (λy.x) 的无名称项是 (λ.0),z(λw.w) 的无名称项是 2(λ.0),2 是 z 在外层的编号(原来的编号)
那么在代换时,z → 2 应当被改变为 z → 3,同时 w → 0 则不应被改变
引入一个移位函数,这个函数携带一个具有截断功能的参数 c $\uparrow_c^d $
c 从 0 开始,每遇到一个绑定器 binder 就 + 1,因此,任意一个索引 k,当 k < c 时是囿界的,k >= c 是一个自由变量
d 代表自由变量的索引增加 d
练习:假定全局上下文是 Γ = a, b 计算 [b → a](b(λx.λy.b))
[b → a](b(λx.λy.b))
[0 → 1](0(λ.λ.2))
1(λ.λ.2[2 → 3])
1(λ.λ.3)
求值
与代换相反,一步求值会消除一个绑定器,应当对层内的自由变量索引 - 1
比如:
(λ.1 0 2) (λ.0) → 0 (λ.0) 1 ≠ 1 (λ.0) 2


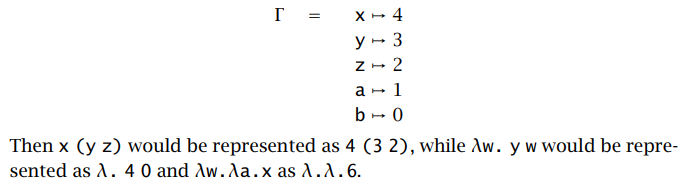

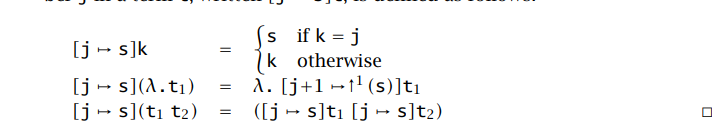

 浙公网安备 33010602011771号
浙公网安备 33010602011771号