5-The Untyped Lambda Calculus
引入
在 lambda 演算中,所有事物都是函数
lambda 演算式中有三种项:
-
变量
x,形如x -
函数抽象
abstraction,形如λx . t1 -
将项
t1作用于t2,形如t1 t2
有如下的简单的递归定义来总结上述三种项的形式:
t ::= x (variable)
λx.t (abstraction)
t t (application)
抽象语法与具体语法
具体语法指程序员直接编写或阅读的代码,比如一段 C++ 代码 x = 1 + 2 * 3;
抽象语法则是更加本质的一种表示,采用抽象语法树 abstract syntax trees 的方式,更清楚地揭示语法中项和项之间关系,对于上面一串代码可能有如下抽象语法树 AST:
=
/ \
x +
/ \
1 *
/ \
2 3
lambda 项表示的是一棵语法树,即使我们写成线性形式(一行)
为了简化 lambda 演算,做出如下两个约定:
-
左结合,意味着
x y t等价于(x y) t -
抽象
abstraction的右部应当尽可能向右拓展(尽可能长),意味着λx . λy . x y x等价于λx . (λy . ((x y) x))
作用域
还需要讨论变量 x 的作用域 scope,也就是 x 什么时候是“自由”的:对于 x,当 x 出现在 λx . t 的 t 中时,我们认为 x 是被约束 bound 的,否则是自由的;我们称 λx 是一个绑定器 binder,t 是这个绑定器的作用域 scope
一个不含自由变量的项成为封闭项(组合子 combinators),最简单的组合子,称为恒等函数,记作 id = λx . x
操作语义
在纯粹的 lambda 运算中,没有内置的常数,原始运算符等等,“运算”的唯一含义是将函数应用 application 于参数(同样也是函数)上
计算(上文所说的 application)的步骤为将左侧的 abstraction 中的约束变量替换成右侧的参数,记作:
(λx . t12) t2 → [x → t2] t12
[x → t2] 意为由 t2 代换在 t12 中所有自由出现的 x
比如: (λx . x) y 经计算之后为 y
由 Church 的定义,[x → t2] t12 称为一个可归约 reduce 表达式 redex reduciable expressions,并且根据上述操作进行计算的操作称为 beta 规约
下面给出了几个求值策略,用来确定项在下一步求值中如何激活这个可归约表达式
- 全
beta规约full beta-reduction:任何时刻都可以归约任何一个redex,比如:
对于 (λx . x)((λx . x)(λz . (λx . x) z)) ≡ id(id(λz . id (z)))
可以从内向外归约 id(id(λz . id (z))) → id(id(λz . z)) → ... → λz . z
显然从外向内归约可以得到一样的结果
-
常规顺序策略
normal order strategy:外面的redex最先归约 -
按名调用策略
call by name strategy:和常规顺序策略类似,但是不允许在abstraction内部进行归约,同样以上文的例子为例,λz . id z被认为不可进行归约,演算进行到λz . id z就停止了 -
按值调用策略
call by value strategy: 最常用的策略;归约外层redex,且一个 redex 会被归约仅当它的参数已经是一个值value,即一个计算已经完成,已经不能被归约的形式,包括 lambda abstractions,numbers,booleans 等。
本书中采用按值调用策略
多参数 multiple arguments 与柯里化 Currying
上文提出的 lambda 演算没有给予多参数很好的支持,一种很优美的解决方法是利用高阶函数来达到这一效果,也就是函数柯里化
函数柯里化的主要思路是,将多参数函数转化为多个单参数的高阶函数,比如:
func(1, 2, 3) → func(1)(2)(3)
采用 lambda 语言书写:
将 f = λ(x, y) . s 写成 f = λx . λy . s,那么对于 f v w 有 (λy . [x → v] s) w [y → w] [x → v] s
题外话,下面给出函数柯里化的一种 js 实现:
function curry(fn) {
return function curried(...args) {
if (args.length >= fn.length) {
return fn.apply(this, args);
} else {
return function(...args2) {
return curried.apply(this, args.concat(args2));
};
}
};
}
// 作者:shichuan
// 链接:https://juejin.cn/post/7215497169469685815
// 来源:稀土掘金
// 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
Church 布尔式
定义项 tru 和 fls 如下所示:
tru = λt . λf . t 表示布尔值“真”
fls = λt . λf . f 表示布尔值“假”
那么就可以定义一个组合子 test b v w,具有类似于 if 的性质,当 b 为 tru 时返回第一个参数 v
定义:
test = λl . λm . λn . l m n
验证:
test tru v w
= (λl . λm . λn . l m n)(tru v w)
= tru v w
= (λt . λf . t)v w
= v
有意思的是,这个 tru 并不符合我们对“真”的直观感觉,但在 lambda 语言里却拥有“真”的运算性质
同样的可以定义 and = λb . λc . b c fls
序偶
pair = λf . λs . λb . b f s
fst = λp . p tru
snd = λp . p fls
验证过程略去
Church 数值
定义 Church 数值 c0, c1, c2:
c0 = λs . λz . z
c1 = λs . λz . s z
c2 = λs . λz . s (s z)
etc
同样可以定义后继函数 scc = λn . λs . λz . s (n s z);后继函数在形式上很容易理解,通俗的说,对于一个给定的 Church 数值 n,代入两个参数 s z,再叠加一次 s
加法 plus = λm . λn . λs . λz . m s (n s z);通俗的说,m + n 即在 n 上做 m 次后继
同理,乘法 times = λm. λn . m (plus n) c0;数学上等价于 n + n + ... + n + 0
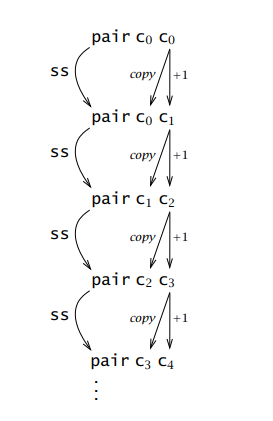
减法的定义要复杂一些,可以借用下面的前驱函数 prd
zz = pair c0 c0
ss = λp . pair (snd p) (plus c1 (snd p))
prd = λm . fst (m ss zz)
减法 sub = λm . λn . n prd m
丰富运算 enrich the calculus
既然布尔表达式和数值都能在这个 lambda 系统中进行表示和运算,那么理论上可以借助 lambda 进行任何程序的设计
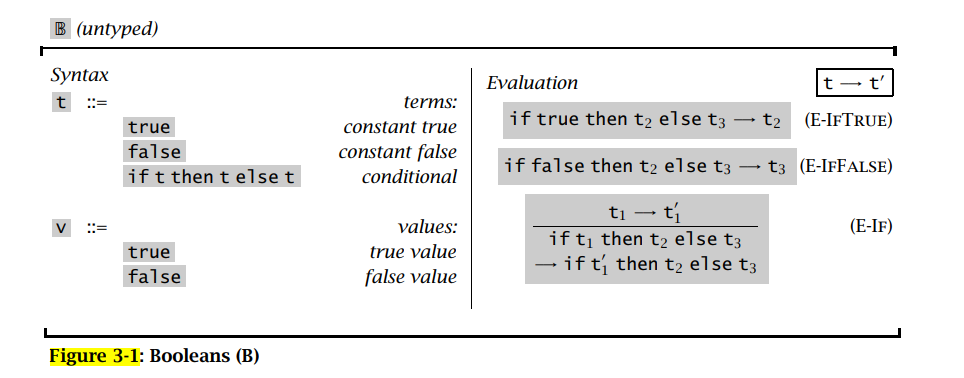
用符号 λ 表示纯粹的 lambda 运算,λNB 表示无类型算术表达式 untyped arithmetic expression 的系统
很容易实现二者之间的转换:
realbool = λb . b true false
churchbool = λb . if b then true else false
在高级一点的操作中也能实现这种转换:
realeq = λm . λn . (equal m n) true false
realnat = λm . m (λx . succ x) 0
使用原始布尔值和数(指 λNB系统)的理由主要与求值策略 evaluation order 有关;前文说过本书主要采用按值调用策略 call by value strategy,考虑对于项 scc c1,这个结果期望是 c2,然而事实上首先会得到一个可归约表达式,经过一到两步归约得到 c2,这一行为在按值调用中是不允许的;这样的话,运算及其结果就会异常复杂
递归
不能继续进行求值的一个项称为一个范式,然而对于下面的 omega,它并不能被求值成一个范式:
omega = (λx . x x) (λx . x x)
对 omega 进行一步归约会产生另一个 omega;omega 有一个有用的推广,称为不动点组合子 fixed-point combinator:
fix=λf.(λx.f (λy.x x y)) (λx.f (λy.x x y)); 或者更简单的按名调用 Y = λf . (λx. f(x x)) (λx. f(x x))
使用方法是:
f = ⟨body containing f⟩ # 对于一个递归函数 f
g = λf.⟨body containing f⟩ # 定义 f 的初步 lambda 形式
h = fix g # 得到递归 lambda 函数
比如对于阶乘函数 factorial 有如下式子:
f = if realeq n c0 then c0
else times n (if realeq n-1 c0 then c0
else times n-1 (...))
g = λf . λn . if realeq n c0 then c1 else times n f (prd n)
h = fix g
前面的 factorial 使用的是 if 而不是 test,是因为在 call-by-value 下,如果要对 test 进行 evaluate,则必须要求出其两个分支的内容后才能进一步 reduce,而这样会导致 diverge
https://roife.github.io/posts/tapl-05/
语法
下面将更加详细地确定 lambda 语法的演算和语义
定义:设 V 是一个变量名的可数集合,项的集合是最小的集合 T
-
对每个
x ∈ V,x ∈ T -
如果
t1 ∈ T 且 x ∈ V,那么λx . t1 ∈ T -
如果
t1 ∈ T 且 t2 ∈ T,那么t1 t2 ∈ T
定义:项 t 的自由变量集合记为 FV(t)
-
FV(x) = x -
FV(λx . t1) = FV(t1) - x -
FV(t1 t2) = FV(t1) + FV(t2)
代换
上面给出了一个简单的代换 (λx . t1) t2 = [x → t2]t1
形式上的定义一个函数 [x → s],有这样一个特殊的例子:
[x → y](λx . x) = λx . y
这个转换将一个恒等函数变换为了一个常量函数
- 第一个错误:
x本来已被界定,代换后变为自由的
[x → z](λz . x) = λz . z
这个转换将一个常量函数变换为了一个恒等函数
- 第二个错误:
x本来是自由变量,代换后变成界定的(变量捕捉)
然后我们稍作修改,可以得到一个几乎正确的定义:
新定义无法操作 [x → y z](λy . x y),问题在于 y
解决这个问题的共同方法是假定项在受界定变量的重新命名下是相同的(在 alpha 转换下是相同的)
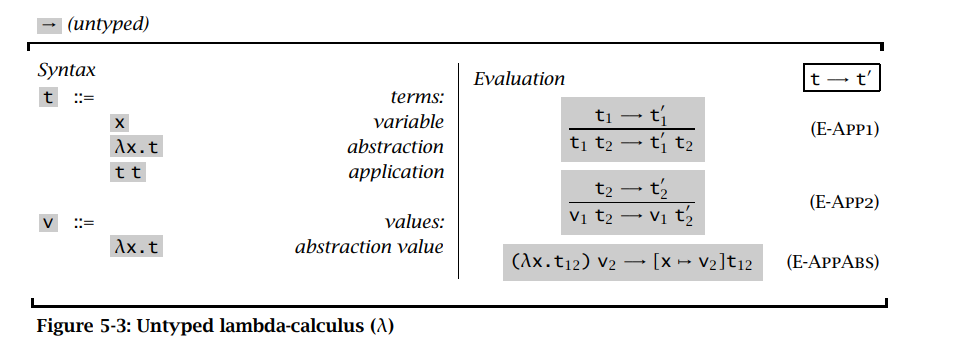
操作语义
这个语义隐含地包含了求值顺序 E-App1 -> E-App2 -> E-AppABS


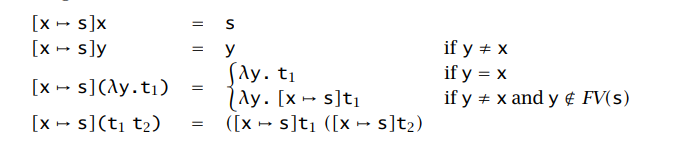

 浙公网安备 33010602011771号
浙公网安备 33010602011771号