一、傅里叶级数
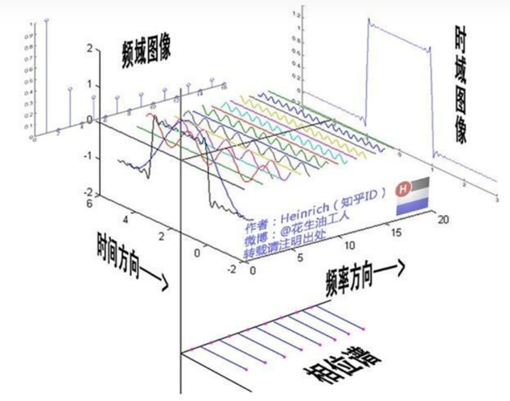
核心思想:周期函数\(f(t)\)可以看成是一系列频率(周期)不同的周期函数\({f_k}(t)\)的叠加,即:
\[\begin{array}{c}
f(t) = {c_1}{f_1}(t) + {c_2}{f_2}(t) + \cdots + {c_n}{f_n}(t)\\
= \sum\nolimits_{k = 1}^n {{c_k}} {f_k}(t)
\end{array}\]
傅里叶级数假设:周期函数${f_k}(t)$的形式为${e^{ik{w_0}t}}$,其中${w_0}$称为基频,${f_k}(t)$的频率为基频${w_0}$的整数倍,则有:
\[\begin{array}{c}
f(t) = \sum\nolimits_{k = - \infty }^{ + \infty } {{c_k}{e^{ik{w_0}{\rm{t}}}}} \\
= \cdots + {c_{ - 2}}{e^{ - 2i{w_0}t}} + {c_{ - 1}}{e^{ - 1i{w_0}t}} + {c_0}{e^{0i{w_0}t}} + {c_1}{e^{1i{w_0}t}} + {c_2}{e^{2i{w_0}t}} + \cdots
\end{array}\]
根据基频${w_0}$,理论上我们可以拟合任意周期函数$f(t)$。可是目前${c_k}$对我们而言仍然是不可知的。于是接下来给出求${c_k}$的方法。
在上式两边同时乘以${e^{in{w_0}t}}$,则有:
\[\begin{array}{c}
f(t){e^{ - in{w_0}{\rm{t}}}} = \sum\nolimits_{k = - \infty }^{ + \infty } {{c_k}{e^{i\left( {k - n} \right){w_0}{\rm{t}}}}} \\
= \cdots + {c_{n - 2}}{e^{ - 2i{w_0}t}} + {c_{n - 1}}{e^{ - 1i{w_0}t}} + {c_n}{e^{0i{w_0}t}} + {c_{n + 1}}{e^{1i{w_0}t}} + {c_{n + 2}}{e^{2i{w_0}t}} + \cdots
\end{array}\]
接下来对上式两边进行积分,根据三角函数性质:
\[\int_0^T {{e^{ - ik{w_0}{\rm{t}}}}} dt = 0\begin{array}{*{20}{c}}
{}&{\left( {k \ne 0,T = \frac{{2\pi }}{{{w_0}}}} \right)}
\end{array}\]
于是积分结果为:
\[\int_0^T {f(t){e^{ - in{w_0}{\rm{t}}}}} dt = \cdots + 0 + 0 + T{c_n} + 0 + 0 + \cdots \]
故:
\[{c_n} = \frac{1}{T}\int_0^T {f(t){e^{ - in{w_0}{\rm{t}}}}} dt\]
称数列${c_k}$为$f(t)$的离散频谱,$\left| {{c_k}} \right|$为$f(t)$的离散振幅谱,$\arg \left( {{c_k}} \right)$为$f(t)$的离散相位谱。
至此,对于任意周期为T,频率为${w_0}$的函数$f(t)$,可以分解为一系列周期函数${e^{ik{w_0}t}}$的线性叠加,即:
\[f(t) = \sum\nolimits_{k = - \infty }^{ + \infty } {{c_k}{e^{ik{w_0}{\rm{t}}}}} \]
\[{c_k} = \frac{1}{T}\int_0^T {f(t){e^{ - ik{w_0}{\rm{t}}}}} dt\]
其中,${w_0}$为基频,${c_k}$的求取方法上文已经给出。
二、傅里叶变换
傅里叶级数有其局限性,即要求$f(t)$为周期函数,而对于非周期函数只能进行有限区间上的拟合。
例如,当$f(t)$为非周期函数,对其在$\left[ {0,T} \right]$上进行拟合,如下图:

于是,人们开始想,能不能对非周期函数$f(t)$进行全局上的拟合呢?
于是,将非周期函数$f(t)$看成一个周期无穷大的周期函数,便得到傅里叶级数的推广——傅里叶积分定理。下面具体介绍推广过程:
对非周期函数$f(t)$在区间$\left[ { - \frac{T}{2},\frac{T}{2}} \right]$上展开为傅里叶级数得:
\[f(t) = \sum\nolimits_{k = - \infty }^{ + \infty } {{c_k}{e^{ik{w_0}{\rm{t}}}}} \]
\[{c_k} = \frac{1}{T}\int_{ - T/2}^{T/2} {f(t){e^{ - ik{w_0}{\rm{t}}}}} dt\]
相邻频率的周期函数得频率间隔为:
\[\Delta w = \left( {k + 1} \right){w_0} + k{w_0} = {w_0}\]
代入上式有:
\[{c_k} = \frac{{\Delta w}}{{2\pi }}\int_{ - T/2}^{T/2} {f(t){e^{ - ik{w_0}{\rm{t}}}}} dt\]
\[\begin{array}{c}
f(t) = \sum\nolimits_{k = - \infty }^{ + \infty } {\left( {\frac{{\Delta w}}{{2\pi }}\int_{ - T/2}^{T/2} {f(t){e^{ - ik{w_0}{\rm{t}}}}} dt} \right){e^{ik{w_0}{\rm{t}}}}} \\
= \frac{1}{{2\pi }}\sum\nolimits_{k = - \infty }^{ + \infty } {\left( {\int_{ - T/2}^{T/2} {f(t){e^{ - ik{w_0}{\rm{t}}}}} dt} \right){e^{ik{w_0}{\rm{t}}}}} \cdot \Delta w
\end{array}\]
将非周期函数$f(t)$看成周期无穷大的周期函数,等价于$\left( {T \to + \infty } \right)$,于是$\Delta w = {w_0} = \frac{{2\pi }}{T} \to 0$,${\rm{k}}{{\rm{w}}_0}$可以视为连续变量。因此接下来如下记作:
\[\mathop {\lim }\limits_{T \to + \infty } \Delta w \Rightarrow dw\]
\[\mathop {\lim }\limits_{T \to + \infty } k{w_0} \Rightarrow w\]
接下来,就有:
\[\begin{array}{c}
f(t) = \mathop {\lim }\limits_{T \to + \infty } \frac{1}{{2\pi }}\sum\nolimits_{k = - \infty }^{ + \infty } {\left( {\int_{ - T/2}^{T/2} {f(t){e^{ - ik{w_0}{\rm{t}}}}} dt} \right){e^{ik{w_0}{\rm{t}}}}} \cdot \Delta w\\
= \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } {\left( {\int_{ - \infty }^{ + \infty } {f(t){e^{ - iw{\rm{t}}}}} dt} \right){e^{iw{\rm{t}}}}} dw
\end{array}\]
上式被称为傅里叶积分定理。
\[F(w) = \xi [f(t)] = \int_{ - \infty }^{ + \infty } {f(t){e^{ - iw{\rm{t}}}}} dt\]
上式即为傅里叶变换(函数的函数)。$F(w)$描述的是$f(t)$中${e^{iwt}}$的分布密度。称$F(w)$为$f(t)$的频谱密度函数(简称为连续频谱或频谱)。$\left| {F(w)} \right|$为$f(t)$的振幅谱,$\arg \left[ {F\left( w \right)} \right]$为$f(t)$的相位谱。
得到频谱函数可以通过傅里叶逆变换变回去,即
\[f(t) = {\xi ^{ - 1}}\left[ {F\left( w \right)} \right] = \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } {F\left( w \right){e^{iw{\rm{t}}}}} dw\]
三、离散傅里叶变换(DFT)
傅里叶变换的目的就是得到信号的频谱密度函数$F(w)$,即:
\[F(w) = \xi [f(t)] = \int_{ - \infty }^{ + \infty } {f(t){e^{ - iw{\rm{t}}}}} dt\]
这里t和w均为连续变量,但是计算机采集的信号在时域上是离散的,即t是离散的,故计算机中储存的是经过采样处理后的${f_s}(t)$。
同时,计算机只能计算出有限个频率对应的幅值密度,即w也是离散的。
因此,DFT是t和w都为离散版的傅里叶变换。
在具体推导DFT之前,先了解冲激函数$\delta (t)$,具有以下性质。
\[\delta (t) = 0\begin{array}{*{20}{c}}
{}&{when t \ne 0}
\end{array}\]
\[\int_{ - \infty }^{ + \infty } {\delta (t)} dt = 1\]
根据定义,有:
\[\int_{ - \infty }^{ + \infty } {\delta (t - {t_0})} f\left( t \right)dt = f\left( {{t_0}} \right)\]
定义梳状函数(用于采样,${T_s}$为采样周期):
\[{\delta _s}(t) = \sum\nolimits_{n = - \infty }^{ + \infty } {\delta (t - n{T_s})} \]
将$f(t)$与它相乘,便得到采样处理后的离散函数:
\[{f_s}(t) = \sum\nolimits_{n = - \infty }^{ + \infty } {f(t)\delta (t - n{T_s})} \]
根据习惯,我们将${f_s}(t)$重新记为${x_s}(t)$,即:
\[{x_s}(t) = \sum\nolimits_{n = - \infty }^{ + \infty } {x(t)\delta (t - n{T_s})} \]
对${x_s}(t)$进行傅里叶变换,有:
\[\begin{array}{c}
{X_s}\left( w \right) = \int_{ - \infty }^{ + \infty } {{x_s}\left( t \right){e^{ - iwt}}dt} \\
= \int_{ - \infty }^{ + \infty } {\left( {\sum\nolimits_{n = - \infty }^{ + \infty } {x(t)\delta (t - n{T_s})} } \right){e^{ - iwt}}dt} \\
= \sum\nolimits_{n = - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {x(t)\delta (t - n{T_s}){e^{ - iwt}}dt} } \\
= \sum\nolimits_{n = - \infty }^{ + \infty } {x(n{T_s}){e^{ - iwn{T_s}}}}
\end{array}\]
我们此时只是对时域进行了离散化,但是${X_s}(w)$在频域上依然是连续的,而计算机只能求取有限个w对应的频谱密度。此外,${X_s}(w)$中的时域采样次数N为无穷大,实际应用中显然不会进行无穷多次时域采样。
我们首先解决N为无穷大的问题。对于连续信号$x(t)$进行N次(N为有限值)采样,采样周期为${T_s}$。然后对采样得到的信号进行时域上的周期延拓(延拓至正负无穷),这样我们就得到了一个周期为${T_0} = N{T_s}$的函数。对于周期函数而言,它的频谱函数是离散化的,这样我们就成功把频域也进行了离散化。具体计算方法如下:
在一个周期内,N次采样离散信号的表达式为:
\[{x_s}(t) = \sum\nolimits_{n = 0}^{N - 1} {x(t)\delta (t - n{T_s})} \]
${x_s}(t)$为离散周期函数,周期${T_0} = N{T_s} = 2\pi /{w_0}$,由傅里叶级数一节,可知:
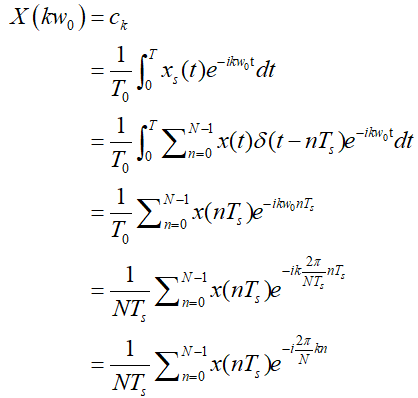
为更加简明,记$X\left[ k \right] = X\left( {k{w_0}} \right)N{T_s}$,$x\left[ n \right] = x\left( {n{T_s}} \right)$,则有:
\[X\left[ k \right] = \sum\nolimits_{n = 0}^{N - 1} {x\left[ n \right]} {e^{ - i\frac{{2\pi }}{N}kn}}\]
对于一个特定k值,求$X\left[ k \right]$,需要N次乘法,(N-1)次加法运算。
而需要这样运算的k值总共有多少个?一般来说,由于${e^{ - i2\pi n\frac{k}{N}}}$的周期性,我们只取0<k<N-1进行运算。可得复杂度为$O\left( {{N^2}} \right)$。我们总算把运算次数变成了有限次。
四、快速傅里叶变换(FFT)
令:
\[W\left[ {n,k} \right] = {e^{ - i\frac{{2\pi }}{N}nk}}\]
因为当n为偶数时(用2n表示),可证明:
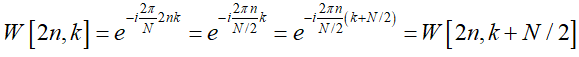
即,当n为偶数时有:
\[W\left[ {n,k} \right] = W\left[ {n,k + N/2} \right]\]
将$X\left[ k \right]$分为n为偶数以及n为奇数两个部分。
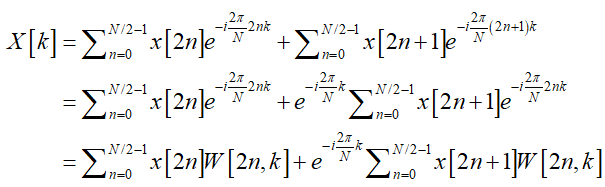
对上式简化处理,将偶数部分记作$E\left[ k \right]$,奇数部分中的求和部分记作$O\left[ k \right]$,则:
\[X\left[ k \right] = E\left[ k \right] + W\left[ {1,k} \right]O\left[ k \right]\]
易证得:
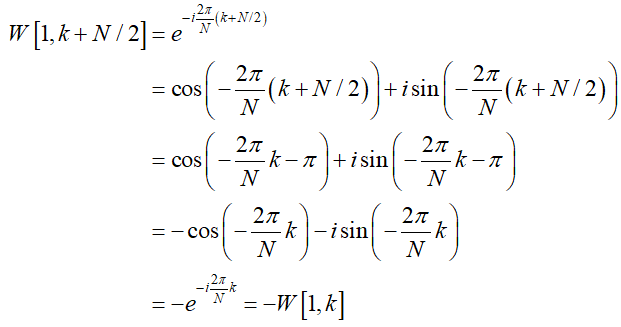
此外,易证得:
\[W\left[ {1,k} \right] = - W\left[ {1,k + N/2} \right]\]
\[E\left[ k \right] = E\left[ {k, + N/2} \right]\]
\[O\left[ k \right] = O\left[ {k, + N/2} \right]\]
因此,有:
\[X\left[ {k + N/2} \right] = E\left[ k \right] - W\left[ {1,k} \right]O\left[ k \right]\]
$E\left[ k \right]$,$O\left[ k \right]$可以继续分解为奇数和偶数部分,此时$N' = N/2$,如此迭代。
示例(N=8):
第一次分解:
$N$=8,n=(0,1,2,3,4,5,6,7),2n=(0,2,4,6),2n+1=(1,3,5,7)
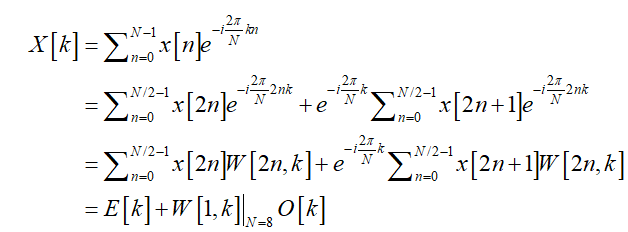
第二次分解:(以$E\left[ k \right]$为例,$O\left[ k \right]$类似)
$N'$=4,n=(0,1,2,3),4n=(0,4),4n+2=(2,6)
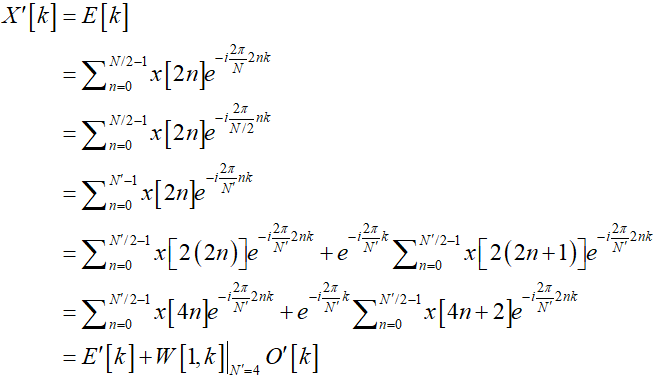
第三次分解:(以$E'\left[ k \right]$为例,$O'\left[ k \right]$类似)
$N''$=2,n=(0,1),8n=0,8n+4=4
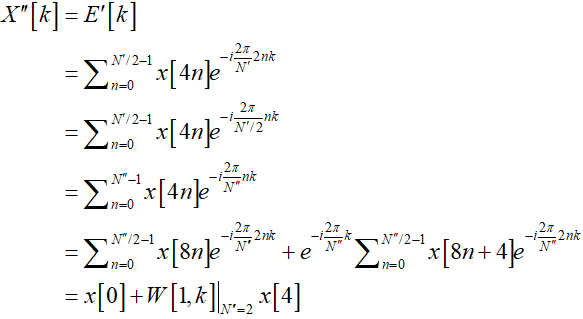
有:
\[X''\left[ 0 \right] = E'\left[ 0 \right] = x\left[ 0 \right] + {\left. {W\left[ {1,0} \right]} \right|_{N'' = 2}}x\left[ 4 \right]\]
\[X''\left[ 1 \right] = E'\left[ 1 \right] = x\left[ 0 \right] - {\left. {W\left[ {1,0} \right]} \right|_{N'' = 2}}x\left[ 4 \right]\]
认识蝶形图:
(1) 级的概念
每分解一次,称为一级运算。设 FFT 运算点数为 N,共有 M 级运算,则它们满足:
\[M = {\log _2}N\]
每一级运算的标识为 m = 0, 1, 2, ..., M-1。为了便于分解计算,FFT 点数 N 的取值经常为 2 的整数次幂。
(2) 蝶形单元
FFT 计算结构由若干个蝶形运算单元组成,每个运算单元示意图如下:
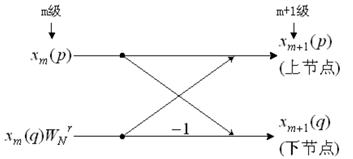
\[{X_{m + 1}}(p) = {X_m}(p) + {X_m}(q)W_N^k\]
\[{X_{m + 1}}(p) = {X_m}(p) - {X_m}(q)W_N^k\]
其中,$q = p + {2^m}$,每一个蝶形单元运算时,进行了一次乘法和两次加法。每一级中,均有 N/2 个蝶形单元。故完成一次 FFT 所需要的乘法次数和加法次数分别为:
\[N/2 \cdot {\log _2}N\]
\[N \cdot {\log _2}N\]
(3) 组的概念
每一级 N/2 个蝶形单元可分为若干组,每一组有着相同的结构与$W_N^k$因子分布。
例如:m=0 时,可以分为 N/2=4 组。
m=1 时,可以分为 N/4=2 组。
m=M-1 时,此时只能分为 1 组。
(3) 因子化简
\[W_N^k = {\left. {W\left[ {1,k} \right]} \right|_N} = {e^{ - i\frac{{2\pi }}{N}k}}\]
\[W_N^k = W_{2N}^{2k}\]
例如,在 8 点 FFT 第二级运算中,即 m=1 ,蝶形运算因子可以化简为:
\[\begin{array}{*{20}{c}}
{W_4^0}&{W_4^1}
\end{array} \Rightarrow \begin{array}{*{20}{c}}
{W_8^0}&{W_8^2}
\end{array}\]
(5) 码位倒置
对于 N=8 点的 FFT 计算,x(0) ~ x(7) 位置对应的 2 进制码为:
X(000), X(001), X(010), X(011), X(100), X(101), X(110), X(111)
将其位置的 2 进制码进行翻转:
X(000), X(100), X(010), X(110), X(001), X(101), X(011), X(111)
此时位置对应的 10 进制为:
X(0), X(4), X(2), X(6), X(1), X(5), X(3), X(7)
恰好对应 FFT 第一级输入数据的顺序,该特性有利于 FFT 的编程实现。
(6) 8点FFT设计
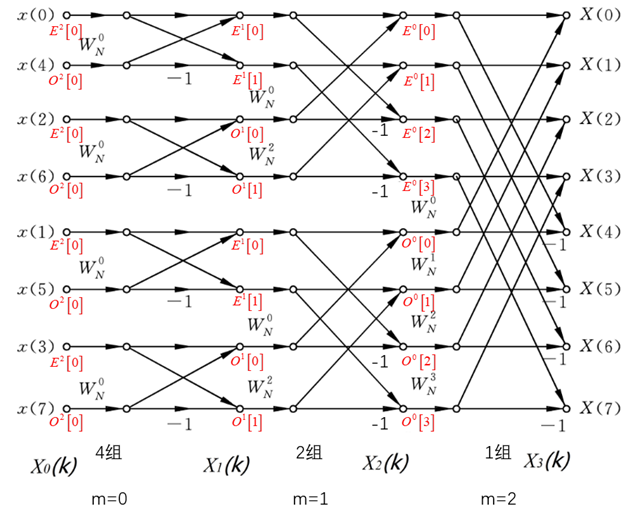
(1) 8 点 FFT 设计,需要 3 级运算,每一级有 4 个蝶形单元,每一级的组数目分别是 4、2、1。
(2) 每一级的组内一个蝶形单元中两个输入端口的距离恒为2m(m 为级标号,对应左移运算 1<<m),组内两个蝶形单元的第一个输入端口间的距离为 1。
(3) 每一级相邻组间的第一个蝶形单元的第一个输入端口的距离为2m+1
参考资料:
1.知乎. Tetradecane. 《积分变换(1)——傅里叶级数》.https://zhuanlan.zhihu.com/p/108017728
2.知乎. Tetradecane. 《积分变换(2)——傅里叶变换》.https://zhuanlan.zhihu.com/p/108271985
3.知乎. cronus-裁.《快速理解FFT算法(完整无废话)》.https://zhuanlan.zhihu.com/p/407885496
4.菜鸟教程.《Verilog FFT 设计》.https://www.runoob.com/w3cnote/verilog-fft.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号