CF895 div3
CF895 div3
A. Two Vessels

题意
有两杯水,一杯有a毫升,另一杯有b毫升,被子的容积无限大。另外还有一个容量为c毫升的杯子,可以用这个杯子在前两个杯子之间舀水,问最少需要几次可以令前两个杯子内的水一样多,舀水的时候不必舀整数毫升。
样例输入
6
3 7 2
17 4 3
17 17 1
17 21 100
1 100 1
97 4 3
样例输出
1
3
0
1
50
16
题解
显然,舀水次数等于ceil(fabs(a - b) / (2c))
#include<iostream>
using namespace std;
inline int Abs(int x) { return x < 0 ? -x : x; }
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int T , a , b , c;
cin >> T;
while(T--)
{
cin >> a >> b >> c;
cout << (Abs(a - b) + 2 * c - 1) / (2 * c) << '\n';
}
return 0;
}
B.The Corridor or There and Back Again
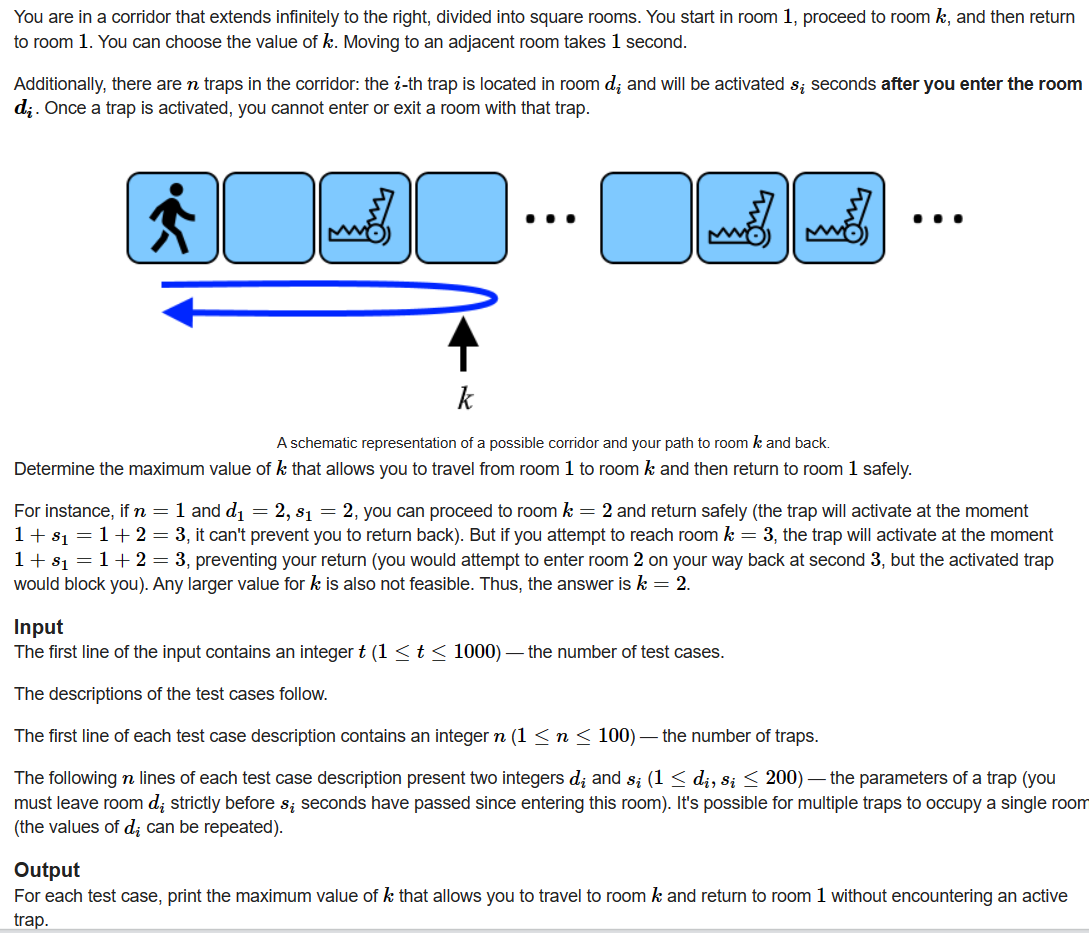
题意
在一排方格中,初始位置在最左侧1号格子里。
有些格子有陷阱,陷阱会在你进入这个格子后的第\(s_i\)秒触发。
不能通过有激活活后陷阱的格子,问最远能到达哪个格子。
样例输入
7
1
2 2
3
2 8
4 3
5 2
1
200 200
4
1 20
5 9
3 179
100 1
2
10 1
1 18
2
1 1
1 2
3
1 3
1 1
1 3
样例输出
2
5
299
9
9
1
1
题解
有陷阱的格子相当于给了一个限制,这个限制类似弹力绳,规定了一个右边界。
比如一个延时s秒之后触发的陷阱,就规定了从此处开始向右行走的距离k满足\(k * 2 < s\),综合所有的限制,就可以得出能到达的最右端了。
#include<iostream>
using namespace std;
const int N = 110;
int n;
struct Node{
int d , s;
}A[N];
void Solve()
{
int Min;
cin >> n;
for(int i = 1 ; i <= n ; ++i)
cin >> A[i].d >> A[i].s;
Min = 500;
for(int i = 1 ; i <= n ; ++i)
Min = min(Min , A[i].d + (A[i].s - 1) / 2);
cout << Min << '\n';
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int T; cin >> T; while(T--) Solve();
return 0;
}
C.Non-coprime Split

题意
给出l,r要求找出一对a,b满足下面的条件
- \(l <= a + b <= r\)
- gcd(a , b) != 1
样例输入
11
11 15
1 3
18 19
41 43
777 777
8000000 10000000
2000 2023
1791791 1791791
1 4
2 3
9840769 9840769
样例输出
6 9
-1
14 4
36 6
111 666
4000000 5000000
2009 7
-1
2 2
-1
6274 9834495
题解
分情况讨论。
如果\(l == r\),令gcd(a,b) = c,那么l也应该是c的倍数,并且l还不能等于c。
所以可以枚举l的约数,看能否找到一个非本身和1的约数,如果可以就令a,b其中一个等于该约数,另一个等于l-约数。
如果\(l != r\),那么判断一下r是否小于4,那么手动枚举一下可以发现,没有解。如果r大于等于4的话,可以选取两个\(\lfloor\frac{r}{2}\rfloor\),这样是绝对满足gcd!=1的。并且\(2 * \lfloor\frac{r}{2}\rfloor\)的值要么等于r,要么等于r-1,所以范围上也是满足的。
#include<iostream>
using namespace std;
int Check(int n)
{
for(int i = 2 ; i * i <= n ; ++i)
{
if(n % i == 0 && n / i >= 2)
return i;
}
return -1;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int T , a , b , d;
cin >> T;
while(T--)
{
cin >> a >> b;
if(a == b)
{
d = Check(a);
if(d != -1)
cout << d << ' ' << a - d << '\n';
else
cout << -1 << '\n';
}
else
{
if(b >= 4)
cout << (b / 2) << ' ' << (b / 2) << '\n';
else
cout << -1 << '\n';
}
}
return 0;
}
D. Plus Minus Permutations

题意
给出n,x,y,要求构造一个长度为n的排列,使得所有下标为x的倍数的数字和所有下标为y的倍数的数字的差值最大。
样例输入
8
7 2 3
12 6 3
9 1 9
2 2 2
100 20 50
24 4 6
1000000000 5575 25450
4 4 1
样例输出
12
-3
44
0
393
87
179179179436104
-6
题解
差值=只是x的倍数的下标对应的值-只是y的倍数的下标对应的值。
可以求出这些下标,然后对于x的部分就安排最大的数字,对于y的部分就安排最小的数字。
#include<algorithm>
#include<iostream>
using namespace std;
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int T;
long long n , x , y , numx , numy , numxy;
cin >> T;
while(T--)
{
cin >> n >> x >> y;
numx = n / x; numy = n / y; numxy = n / ((x * y) / __gcd(x , y));
numx -= numxy; numy -= numxy;
cout << (n - numx + 1 + n) * numx / 2 - (1 + numy) * numy / 2 << '\n';
}
return 0;
}
E.Data Structures Fan

题意
给出一个序列a和一个01字符串s,有两种操作。
第一种,1 l r 要求将字符串s的[l , r]部分取反。
第二种,2 g,其中g=1或者g=0,要求将字符串s中等于g的位置对应的a序列上的值异或起来并输出。
也就是如果s[i]==g,那么对应的a[i]就要加入异或,最后输出结果。
数据范围是1e5
输出样例
5
5
1 2 3 4 5
01000
7
2 0
2 1
1 2 4
2 0
2 1
1 1 3
2 1
6
12 12 14 14 5 5
001001
3
2 1
1 2 4
2 1
4
7 7 7 777
1111
3
2 0
1 2 3
2 0
2
1000000000 996179179
11
1
2 1
5
1 42 20 47 7
00011
5
1 3 4
1 1 1
1 3 4
1 2 4
2 0
输出样例
3 2 6 7 7
11 7
0 0
16430827
47
题解
题目中只设计字符串s的修改,序列a中没有改变。
维护两个变量Answer0,Answer1,分别表示s中0对应的位置的异或和s中1对应位置的异或。
对于操作2,直接输出即可。
对于操作1,将s取反,对于Answer0和Answer1都是异或上这段区间的区间异或和。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int n;
int Array[N] , Sum[N];
char String[N];
int Solve()
{
int Q , opt , l , r , x , Answer0 , Answer1;
cin >> n;
for(int i = 1 ; i <= n ; ++i)
cin >> Array[i];
cin >> (String + 1);
for(int i = 1 ; i <= n ; ++i)
Sum[i] = Sum[i-1] ^ Array[i];
Answer0 = Answer1 = 0;
for(int i = 1 ; i <= n ; ++i)
if(String[i] == '0')
Answer0 ^= Array[i];
else
if(String[i] == '1')
Answer1 ^= Array[i];
cin >> Q;
while(Q--)
{
cin >> opt;
if(opt == 1)
{
cin >> l >> r;
Answer0 ^= Sum[r] ^ Sum[l-1];
Answer1 ^= Sum[r] ^ Sum[l-1];
}
else
{
cin >> x;
if(x == 0)
cout << Answer0 << ' ';
else
cout << Answer1 << ' ';
}
}
cout << '\n';
return 0;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int T; cin >> T; while(T--) Solve();
return 0;
}
F.Selling a Menagerie

题意
马戏团里有n只动物,每只动物i都有唯一一个害怕的其它动物a[i],现在要将这些动物一个接一个地卖出去。如果动物i卖出的时候,它害怕的动物a[i],还没被卖出,那么动物i就可以卖出双倍的价格。反之就只有一倍的价格。
现在要求构造一个排列,使得获利最大。
输入样例
8
3
2 3 2
6 6 1
8
2 1 4 3 6 5 8 7
1 2 1 2 2 1 2 1
5
2 1 1 1 1
9 8 1 1 1
2
2 1
1000000000 999999999
7
2 3 2 6 4 4 3
1 2 3 4 5 6 7
5
3 4 4 1 3
3 4 5 6 7
3
2 1 1
1 2 2
4
2 1 4 1
1 1 1 1
输出样例
1 2 3
2 4 5 1 6 3 7 8
3 4 5 1 2
1 2
7 5 1 3 2 6 4
5 3 2 4 1
3 2 1
3 4 1 2
题解
将所有的<a[i] , i>连边,那么得到的图中,最多出现一个环。
在这个图中,取没有出度的点,可以获得两倍的收益。
对于环上的点,则只有一个点不能有两倍收益。
所以,先取没有出度的点,如果碰到了环,则找到环上权值最小的点,然后令最小权值的点只能卖出单倍的价格,换上其它点都是双倍的价格。
#include<iostream>
using namespace std;
const int N = 1e5+10;
long long Answer;
int n , Cnt , Top , Tmp , Tag;
int A[N] , C[N] , head[N] , Stack[N] , Visit[N] , tmp[N] , Output[N];
struct edge{
int v , nex;
}e[N];
inline void add(int u , int v)
{
e[++Cnt].v = v; e[Cnt].nex = head[u]; head[u] = Cnt;
}
void dfs(int x)
{
Visit[x] = Tag; Stack[++Top] = x;
for(int i = head[x] ; i ; i = e[i].nex)
{
int v = e[i].v;
if(!Visit[v]) dfs(v);
else
{
if(Visit[v] != Tag) continue;
int t; Tmp = 0;
do
{
t = Stack[Top--]; tmp[++Tmp] = t;
Output[t] = 1;
}while(t != v);
}
}
if(Top && !Output[Stack[Top]])
Output[Stack[Top]] = 1 , cout << Stack[Top--] << ' ';
}
void Solve()
{
cin >> n;
for(int i = 1 ; i <= n ; ++i) cin >> A[i];
for(int i = 1 ; i <= n ; ++i) cin >> C[i];
for(int i = 1 ; i <= n ; ++i)
add(A[i] , i);
for(int i = 1 ; i <= n ; ++i) if(!Visit[i])
{
++Tag; Tmp = 0;
dfs(i);
if(Tmp)
{
int Min = -1 , pos = -1;
for(int i = 1 ; i <= Tmp ; ++i)
if(Min == -1 || C[Min] > C[tmp[i]])
Min = tmp[i];
for(int i = 1 ; i <= Tmp ; ++i)
if(tmp[i] == Min) { pos = i; break; }
for(int i = 1 ; i <= Tmp ; ++i)
{
pos = pos + 1;
if(pos == Tmp + 1) pos = 1;
cout << tmp[pos] << ' ';
// Output[tmp[pos]] = 1;
}
Tmp = 0;
}
}
cout << '\n';
Top = Cnt = Tag = Tmp = 0;
for(int i = 1 ; i <= n ; ++i)
Visit[i] = Output[i] = head[i] = 0;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int T; cin >> T; while(T--) Solve();
return 0;
}
G.Replace With Product

题意
给一个序列,可以操作最多一次,选择一个区间[l , r]将其替换为区间内所有数的乘积,问最后序列之和的最大值是多少?
输入样例
9
4
1 3 1 3
4
1 1 2 3
5
1 1 1 1 1
5
10 1 10 1 10
1
1
2
2 2
3
2 1 2
4
2 1 1 3
6
2 1 2 1 1 3
输出样例
2 4
3 4
1 1
1 5
1 1
1 2
2 2
4 4
1 6
题解
只有在序列元素为1的时候,选择乘法才比较亏。
如果整个序列的乘积足够大的话,选择整个序列(不含前缀和后缀1)做乘积是比较优的。
如果序列乘积并没有很大的话,那么序列中大于1的数字的个数也不会很多。
这时就可以枚举这些大于1的数字,以它们作为左右边界,选最大值即可。
#include<iostream>
using namespace std;
const int N = 2e5+10;
int n;
int A[N] , t[666];
long long Sum[N];
void Solve()
{
int flag = 0 , m = 0 , L , R;
double Mul = 1.0;
long long tmp , res , Max;
cin >> n;
for(int i = 1 ; i <= n ; ++i) cin >> A[i];
for(int i = 1 ; i <= n ; ++i)
{
Mul = Mul * A[i];
if(Mul > 1e16) { flag = 1; break; }
}
if(flag)
{
for(int i = 1 ; i <= n ; ++i) if(A[i] > 1) { cout << i << ' '; break; }
for(int i = n ; i >= 1 ; --i) if(A[i] > 1) { cout << i << '\n'; break; }
}
else
{
res = 1; Max = 1; L = 1; R = 1;
for(int i = 1 ; i <= n ; ++i)
if(A[i] > 1) t[++m] = i;
for(int i = 1 ; i <= n ; ++i) Sum[i] = Sum[i-1] + A[i];
for(int i = 1 ; i <= m ; ++i)
{
res = 1;
for(int j = i ; j <= m ; ++j)
{
res = res * A[t[j]];
tmp = Sum[t[i] - 1] + Sum[n] - Sum[t[j]] + res;
if(tmp > Max)
L = t[i] , R = t[j] , Max = tmp;
}
}
cout << L << ' ' << R << '\n';
}
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int T; cin >> T; while(T--) Solve();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号