数据结构期末复习知识点总结（二）——树，图（未完结）

数据结构期末知识点总结

一. 树与二叉树

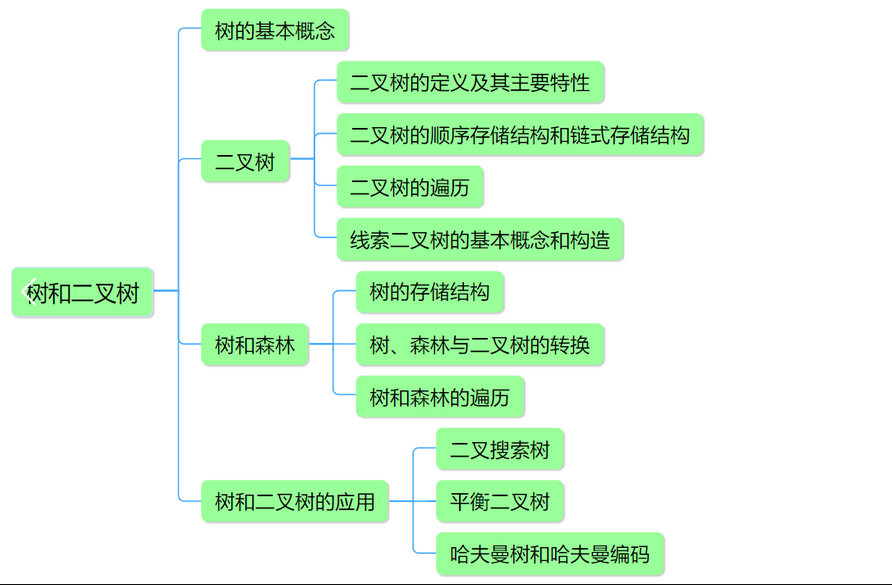
树和二叉树相关概念

基本知识概念

• 树：n个结点的有限集合（n>=0）n为0时为空树。树中有一个根结点，它没有直接前驱，有零个或多个直接后继，根结点之外的n-1个结点可以划分成m个互不相交的有限集，这些有限集称为根的子树（子树互不相交）。

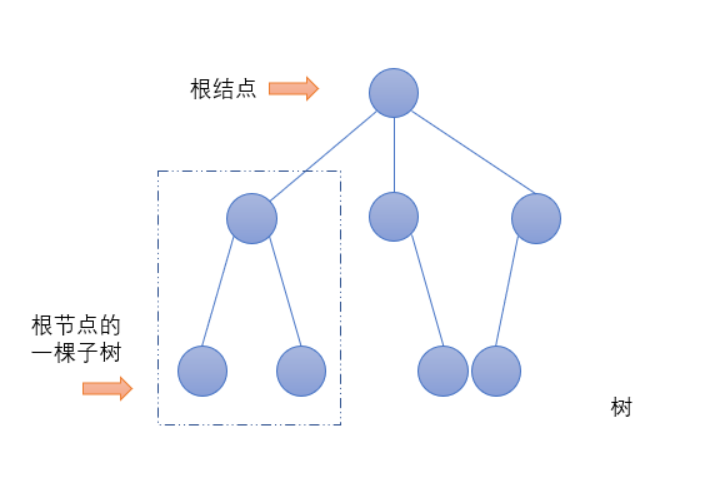
• 二叉树：有限的结点的集合，由根结点和不相交的二叉子树组成

和二叉树的联系与区别

满足以下两个条件的树形结构叫做二叉树：

每个结点至多只有两棵子树
二叉树的子树有左右之分，其次序不能颠倒。树可以有序可以无序

因此树和二叉树结构不等价

【孩子与双亲：结点若有直接后继，则可称它为它直接后继结点的父亲或双亲，直接后继结点为它的孩子，位于左边的孩子叫做左孩子，位于右边的孩子叫做右孩子】

树的基本术语

• 结点的度：子结点或非空子树的个数
• 树的度：树中所有结点的度的最大值
• 叶结点：树中度为0的结点
• 中间结点：树中叶结点以外的结点，亦称内部结点
• 兄弟结点：父结点相同的结点彼此是兄弟结点
• 结点的层次：根结点在第1层；如果结点的层次是𝑘 (𝑘≥1) ，则其子结点都在第𝑘+1层。亦称结点的深度
• 结点的高度：叶结点的高度等于1；中间结点的高度等于其所有子结点的高度的最大值加1
• 树的高度：根结点的高度，亦称树的深度
• 有序树：树中各结点的子树从左向右依次排列，不能交换次序；否则称作无序树
• 森林：零个或多个互不相交（独立）的树的集合
• 祖先结点：根没有祖先；父结点以及父结点的祖先都是结点的祖先结点
• 子孙结点：叶结点没有子孙；中间结点的各子结点以及子结点的子孙都是它的子孙结点

树的基本操作

InitTree(tree):初始化一个空树tree
CreatTree(tree,definition):按照definition构造一个树
IsEmpty(tree):树tree为空返回true,否则返回false
Root(tree):返回树tree的根结点
Get(tree, node):返回树tree的结点node的值
Parent(tree,node):返回树tree中结点node的父结点
GetChild(tree,node,k):返回树tree中结点node的第k个子树
InsertChild(tree,node,k,subtree):将树subtree插入到树tree中，使其成为结点node的第k个子树
Search(tree,x):在树tree中查找值为x的结点，如果查找成功，返回结点，否则返回NIL
Traverse(tree):访问树tree中每个结点，且每个结点只访问一次

二叉树的基本操作

BinaryTreeNodeO:创建一个二叉树结点
CreatBinaryTree(value,left_tree,right_tree):构造二叉树，根结点的数据为value,
左子树和右子树分别是left_tree和right_tree
IsLeaf(tree,node):如果二叉树tree中结点node为叶结点，返回true；否则返回false
Height(tree):返回二叉树tree的高度（深度）
PreOrder(tree):前序遍历二叉树tree
InOrder(tree):中序遍历二叉树tree
PostOrder(tree):后序遍历二叉树tree
LevelOrder(tree):层序遍历二叉树tree

满二叉树与完全二叉树

• 满二叉树：每层结点均满，每层均具有最大结点数，又称完美二叉树
• 完全二叉树：与满二叉树的编号对应，但不要求每层均具有最大结点数

区别于联系：满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树

1. 树的基本性质：

树中所有结点数等于所有结点的度数之和加1

2. 二叉树的基本性质

性质1：二叉树第i层上至多有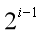
个节点

性质2：深度为k的二叉树最多有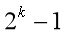
个结点

性质3：任何一颗二叉树，若其叶子节点数为n0,度为2的节点数为n2，则n0=n2+1

性质4：具有n个节点的完全二叉树的深度为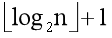

（向下取整）

3. 特殊二叉树

满二叉树：深度为k且含有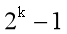
个结点的二叉树，对于编号为i的结点，若存在左孩子，则左孩子编号为2i，右孩子为2i+1

完全二叉树：满二叉树的子图（没有左子树不能有右子树，上一层没有铺满不能有下一层）

二叉树的主要存储方式：顺序存储 + 链接存储

完全二叉树的顺序存储：完全二叉树所有结点可以分层从左向右连续编号，可用一组地址连续的存储单元（顺序表）存储二叉树的各个结点

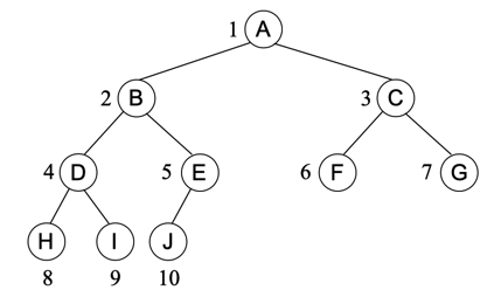
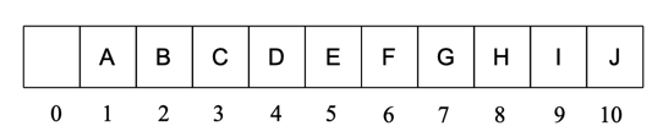
非完全二叉树的顺序存储结点编号：树根的索引为1；设结点的编号为𝑘 (𝑘≥1)，如果其左子树非空，则左子结点的编号为2𝑘；如果右子树非空，则右子结点为2𝑘+1顺序存放：用一组地址连续的存储单元存储二叉树的各个结点

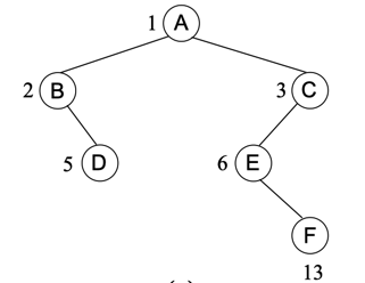
二叉树的创建以及遍历（先序，中序，后序以及先序非递归）

二叉树的链式结构

typedef struct TreeNode{
	char data;
	TreeNode* lchild;
	TreeNode* rchild;
}TreeNode;
typedef TreeNode *BiTree;

二叉树的创建

void createTree(BiTree* T) {  // 参数：指向二叉树节点指针的指针
    char ch;
    scanf("%c", &ch);         // 读取用户输入的字符
    if(ch == '#') {           // 如果输入'#'表示空节点
        *T = NULL;            // 将当前节点指针设为NULL
    }
    else {
        // 动态分配新节点内存
        *T = (BiTree)malloc(sizeof(TreeNode));  
        (*T)->data = ch;      // 将输入字符存入节点
        // 递归创建左子树（注意：&((*T)->lchild)是取左孩子指针的地址）
        createTree(&((*T)->lchild));  
        // 递归创建右子树
        createTree(&((*T)->rchild));  
    }
}

前序遍历

void preOrder(BiTree T){
	if(T==NULL){
		return;
	}
	printf("%c",T->data);
	preOrder(T->lchild);
	preOrder(T->rchild);
}

中序遍历

void inOrder(BiTree T){
	if(T==NULL){
		return;
	}
	inOrder(T->lchild);
	printf("%c",T->data);
	inOrder(T->rchild);
} 

后序遍历

void postOrder(BiTree T){
	if(T==NULL){
		return;
	}
	postOrder(T->lchild);
	postOrder(T->rchild);
	printf("%c",T->data);
} 

先根序非递归

void preorderTraversal2(BiTree root) {
    if (root == NULL) return;
    Stack stk;
    initStack(&stk);
    push(&stk, root);
    while (!isEmpty(&stk)) {
        BiTree node = pop(&stk);
        printf("%c ", node->data);
        if (node->rchild != NULL) push(&stk, node->rchild);
        if (node->lchild != NULL) push(&stk, node->lchild);
    }
}

二叉树遍历性质：

已知前序遍历和中序遍历，可以唯一确定一棵二叉树

已知中序遍历和后序遍历，可以唯一确定一棵二叉树

已知前序遍历和后序遍历，不能唯一确定一棵二叉树