直接插入和希尔排序的缠绵交错
1.问题的提出
数据结构课上我们学习了排序的内容,包括以下这些:冒泡排序,选择排序,插入排序,希尔排序,归并排序,快速排序,堆排序,计数排序,桶排序和基数排序。 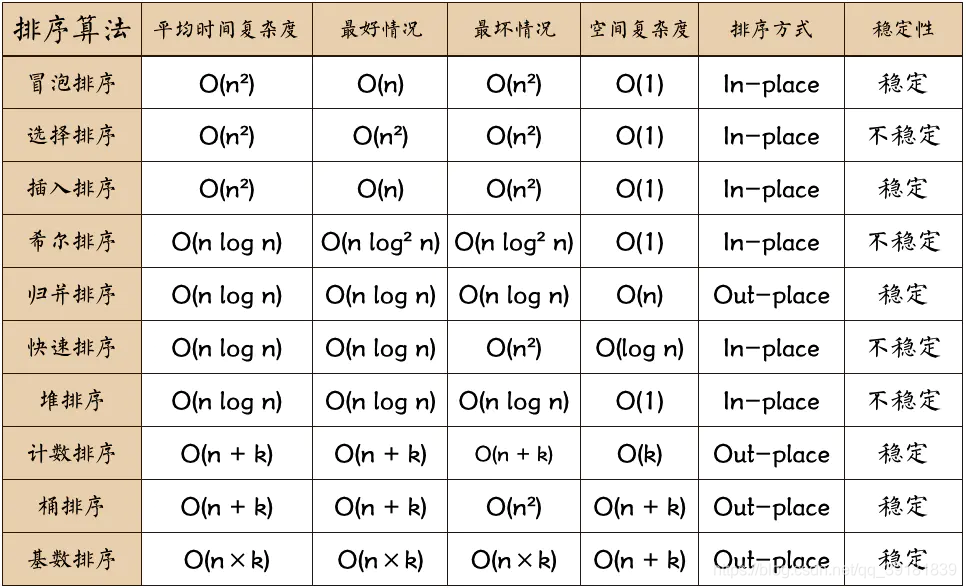
这些排序算法各有各的魅力,但又有其缺陷,可以想到一个人最完美的地方之一也许就是允许自己不完美,时间与空间不能两全,也许这就是算法的美所在,我允许你的不完美,成就了如此多样的你。而每一个你又是如此的令我着迷。
算法的不完美,激起我的探索欲,既然每一种算法都有其独特的地方,何不比较一下他们之间又有什么关联。我们知道算法的快慢与算法本身有关也有数据量的大小有关,而排序本质就是比较,移动两个操作。是不是有可能数据在某个范围内,A算法优于B算法,而大于这个范围B算法优于A算法。为此我选择比较两种有着独特关联的排序算法在不同的数据量条件下他们的的比较和移动次数来探索在不同数据量的情况下,他们的次数如何比变化。
希尔排序中直接用到直接插入算法,可以说直接插入是希尔排序的重要组成部分,没有直接插入就美有希尔排序。
2、基本理论基础
直接插入排序: 英文名:Straight Insertion Sort
也是一种最简单的排序方法,其基本操作是将一条记录插入到已排好的有序表中,从而得到一个新的、记录数量增1的有序表 。
基本原理:将未排序部分的元素逐个插入到已排序部分的正确位置,逐步构建有序序列。
算法步骤
- 初始化:将第一个元素视为已排序序列。
- 遍历未排序元素:从第二个元素开始,逐个与已排序序列的元素比较。
- 插入操作:
- 若当前元素 < 已排序元素,则将已排序元素向后移动一位。
- 重复此过程,直到找到当前元素的正确位置。
- 插入元素:将当前元素放入正确位置,已排序序列长度+1。
- 重复:直至所有元素处理完毕。
例子:以下用数组2,5,8,3,6,9,1,4,7为例,从小到大排序 。
1.先看第一个数,将数****组划分为有序和无序部分
首先看第一个数2,一个数必然有序,所以将2划分有序,后面都是无序

2.无序部分的首个插入到有序部分
取出无序部分的首个,在有序部分从后向前比较,插入到合适的位置
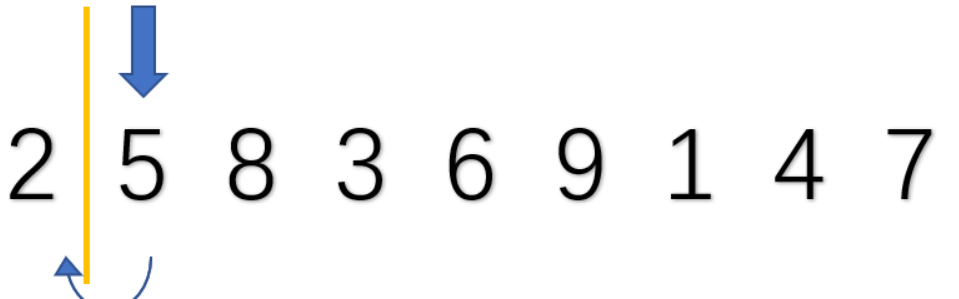


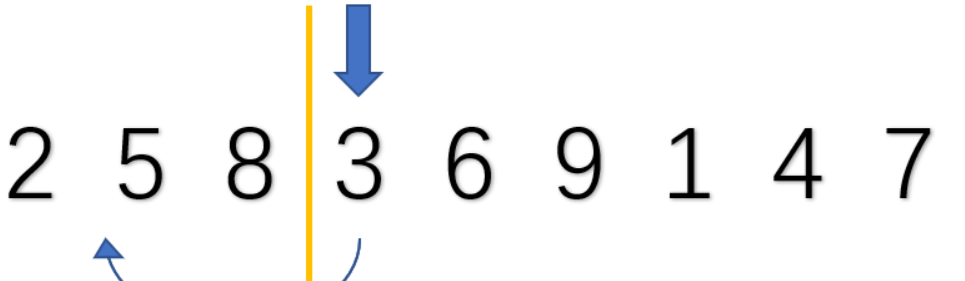
3.重复第2步直到无序部分全部插入有序
8也是一次比较就可以插入



3就需要多次比较,注意是多次比较,直接插入,不是比较一次插入一次(与冒泡不同 )

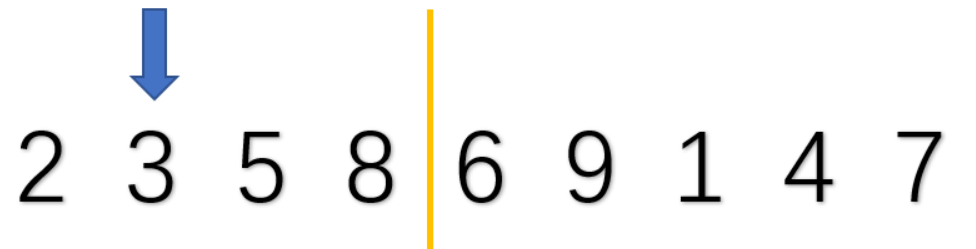
从以上过程可得,这个算法是遍历一次所有数,分别插入,但第一个数一定有序,不用排,因此n个数需要n-1次遍历,即i直接从1开始,每一次插入的比较都是从前一个数开始,所以我们可以直接将第二个循环的参数j设为i-1。
直接插入算法代码
1.时间复杂度
最好情况就是全部有序,此时只需遍历一次,最好的时间复杂度为 O ( n )
最坏情况全部反序,内层每次遍历已排序部分,最坏时间复杂度为 O ( (1+2+……+n+1)/2 )
2.空间复杂度:平均的空间复杂度为: O ( 1 )
3.算法稳定性:相同元素的前后顺序是否改变,插入到比它大的数前面,所以直接插入排序是稳定的
#include <iostream>
using namespace std;
template<class T>
void InsertSort(T a[],int l) {
T temp;
int j;
for (int i = 1; i < l; i++) {
if (a[i] < a[i - 1]) {
temp = a[i];
for (j = i - 1; j >= 0 && temp < a[j]; j--) {
a[j + 1] = a[j];
}
a[j + 1] = temp;
}
}
}
//测试
int main()
{
float a[10] = { 2,5,8,3,6,9,1,4,7,10 };
int len = sizeof(a)/sizeof(a[0]);
cout << len << endl;
InsertSort<float>(a, len);
//测试
for (int k = 0; k < len; k++)
cout << a[k] << " ";
cout << endl;
return 0;
}

**希尔排序: 英文名:Shell’s Sort **
是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。该方法因 D.L.Shell 于 1959 年提出而得名。
基本原理:希尔排序是 插入排序的优化版本,通过 分组插入+逐步缩小区间 的策略减少无效比较和移动。其核心思想是:将原始数组按间隔(gap)分组,对每组进行插入排序,逐步缩小gap直至1,最终完成整体排序。
算法步骤
- 选择增量序列(gap):初始通常取
gap = n/2,后续每次减半。 - 分组插入排序:对每个gap值,将数组分为gap组,每组进行插入排序。
- 缩小gap:重复步骤2,直到gap=1(此时退化为标准插入排序,但数据已部分有序)。
- 最终排序:当gap=1时,执行最后一次插入排序,完成整个数组的排序。
例子:以下用数组2,5,8,3,6,9,1,4,7,0为例,从小到大排序 。
1.先取一个小于n的整数d1作为第一个增量,把数据分组
一般来说取n/2作为d1,所以当前是5
现在相同颜色的就是一组

2.每组进行直接插入排序
首先2和9位置不变, 然后5和1,需要改变,注意是组内直接插入,然后8和4 , 3和7 , 6和0 。


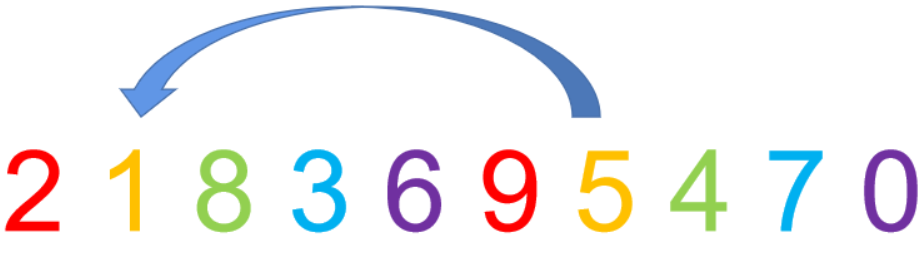

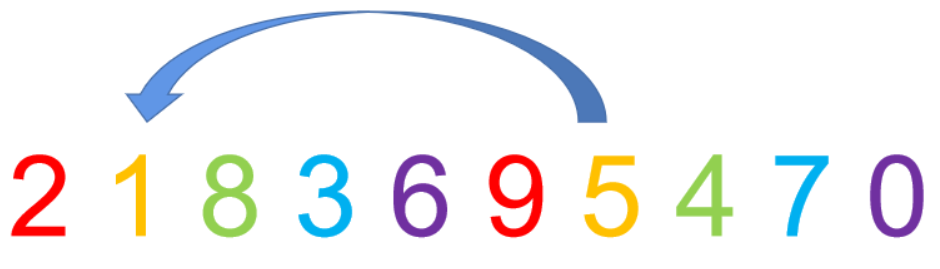

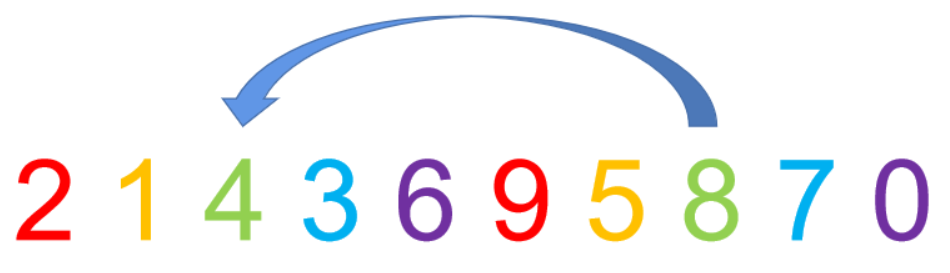

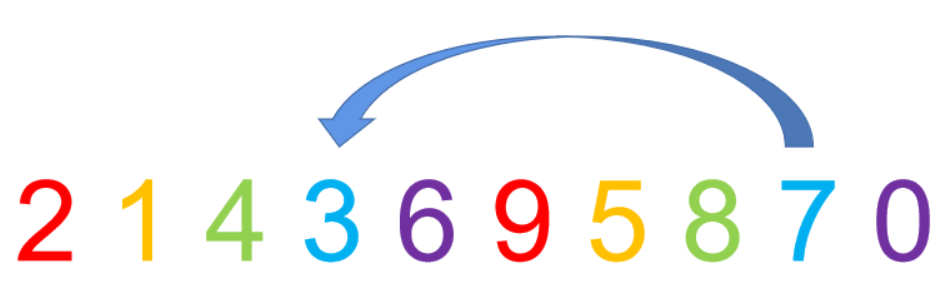

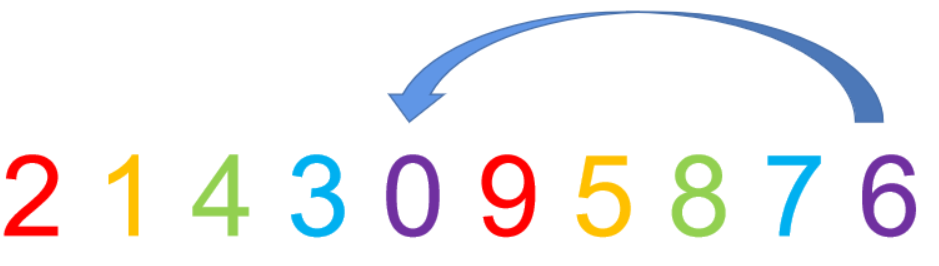
3.缩小增量并重复第二步
希尔排序算法代码
1.时间复杂度:常见结果:O(nlogn)
2.空间复杂度:和直接插入一样,平均的空间复杂度为: O ( 1 ) O(1) O(1)
3.算法稳定性:相同元素的前后顺序是否改变,举个很简单的例子:2 1 1 2,如果gap=2,第三个一会移
动到第一个1前面, 所以希尔排序排序是不稳定的
#include<iostream>
using namespace std;
template<class T>
void ShellSort(T a[], int len)
{
T temp;
int j;
int gap = len / 2;
while(gap) {
for (int i = gap; i < len; i++)
{
if (a[i] < a[i - gap])
{
temp = a[i];//取出改变值
for (j = i - gap; j >= 0 && a[j] > temp; j -= gap)
{
a[j + gap] = a[j];//右移
}
a[j + gap] = temp;
}
}
gap /= 2;
}
}
int main()
{
float a[10] = { 2.0,5.8,8.6,3.4,6.8,9.3,1.3,4.5,7.2,0.0 };
int len = sizeof(a) / sizeof(a[0]);
cout << len << endl;
ShellSort<float>(a, len);
for (int k = 0; k < len; k++)
cout << a[k] << " ";
cout << endl;
return 0;
}

3、代码实现过程
采用表格比较,折线图比较来展示两个算法随数据变化时,比较次数和移动次数的变化过程,采用的
折线图实现方法是把C++得到的数据存到csv文件中,通过python读取文件内容,在通过pandas读
取csv文件,利用matplotlib作图进行可视化操作.
C++代码实现
头文件
#include <cstdint>
#include<iostream>
using namespace std;
template<class T>
void ShellSort(T a[], int len, uint64_t& comparecount, uint64_t& movecount)
{
T temp;
int j;
int gap = len / 2;
comparecount = 0;
movecount = 0;
while (gap) {
for (int i = gap; i < len; i++)
{
comparecount++;
if (a[i] < a[i - gap])
{
temp = a[i];
for (j = i - gap; j >= 0 && a[j] > temp; j -= gap)
{
comparecount++;
a[j + gap] = a[j];
movecount++;
}
comparecount++;
a[j + gap] = temp;
movecount++;
}
}
gap /= 2;
}
}
template<class T>
void InsertSort(T a[], int l, uint64_t& compareCount, uint64_t& moveCount)
{
T temp;
int j;
compareCount = 0;
moveCount = 0;
for (int i = 1; i < l; i++)
{
compareCount++;
if (a[i] < a[i - 1])
{
temp = a[i];
compareCount++;
for (j = i - 1; j >= 0 && temp < a[j]; j--)
{
compareCount++;
if (temp < a[j])
{
a[j + 1] = a[j];
moveCount++;
}
}
a[j + 1] = temp;
moveCount++;
}
}
}
template <typename T>
T* generateRandomArray(int len) {
T* arr = new T[len];
srand(time(0));
for (int i = 0; i < len; i++) {
arr[i] = static_cast<T>(rand() % 10000) / 100.0;
}
return arr;
}
主函数cpp文件
#include <fstream>
#include <cstdint>
#include<iostream>
#include <iomanip>
#include "XIER.h"
#include <cmath>
#include <ctime>
using namespace std;
// 释放动态数组
template <typename T>
void freeArray(T* arr) {
delete[] arr;
}
int main() {
ofstream outfile("sort_data.csv"); // 创建数据文件
outfile << "DataSize,ShellCompare,ShellMove,InsertCompare,InsertMove\n";
cout << "+------------+---------------------+---------------------+\n";
cout << "| 数据量 | 希尔排序 | 直接插入排序 |\n";
cout << "+------------+----------+----------+----------+----------+\n";
cout << "| | 比较次数 | 移动次数 | 比较次数 | 移动次数 |\n";
cout << "+------------+----------+----------+----------+----------+\n";
for (int exp = 1; exp <= 5; exp++) {
int len = pow(10, exp);
//int len = exp;
uint64_t shellCompare, shellMove, insertCompare, insertMove;
double* a = generateRandomArray<double>(len);
double* b = generateRandomArray<double>(len);
std::copy(a, a + len, b);
ShellSort<double>(a, len, shellCompare, shellMove);
InsertSort<double>(b, len, insertCompare, insertMove);
// 写入CSV文件
outfile << len << ","
<< shellCompare << "," << shellMove << ","
<< insertCompare << "," << insertMove << "\n";
cout << "| " << left << setw(10) << len << " | "
<< right << setw(8) << shellCompare << " | "
<< setw(8) << shellMove << " | "
<< setw(8) << insertCompare << " | "
<< setw(8) << insertMove << " |\n";
delete[] a;
delete[] b;
}
cout << "+------------+----------+----------+----------+----------+\n";
outfile.close();
cout << "数据已保存到 sort_data.csv" << endl;
return 0;
}
python可视化实现代码
绘制折线图
import os
import pandas as pd
import matplotlib.pyplot as plt
csv_path = r"C:\Users\寒傲冬雪\Desktop\洛谷\数据结构\sort_data.csv"
data = pd.read_csv(csv_path)
plt.figure(figsize=(10, 6))
plt.plot(data["DataSize"], data["ShellCompare"], label="Shell Sort (Compare)", marker="o")
plt.plot(data["DataSize"], data["InsertCompare"], label="Insert Sort (Compare)", marker="s")
plt.plot(data["DataSize"], data["ShellMove"], label="Shell Sort (Move)", linestyle="--", marker="o")
plt.plot(data["DataSize"], data["InsertMove"], label="Insert Sort (Move)", linestyle="--", marker="s")
plt.xscale("log")
plt.yscale("log")
plt.xlabel("Data Size")
plt.ylabel("Count")
plt.title("Sorting Algorithm Performance")
plt.legend()
plt.grid(True)
plt.savefig("sort_comparison.png")
plt.show()
4、实验数据分析
表格比较:
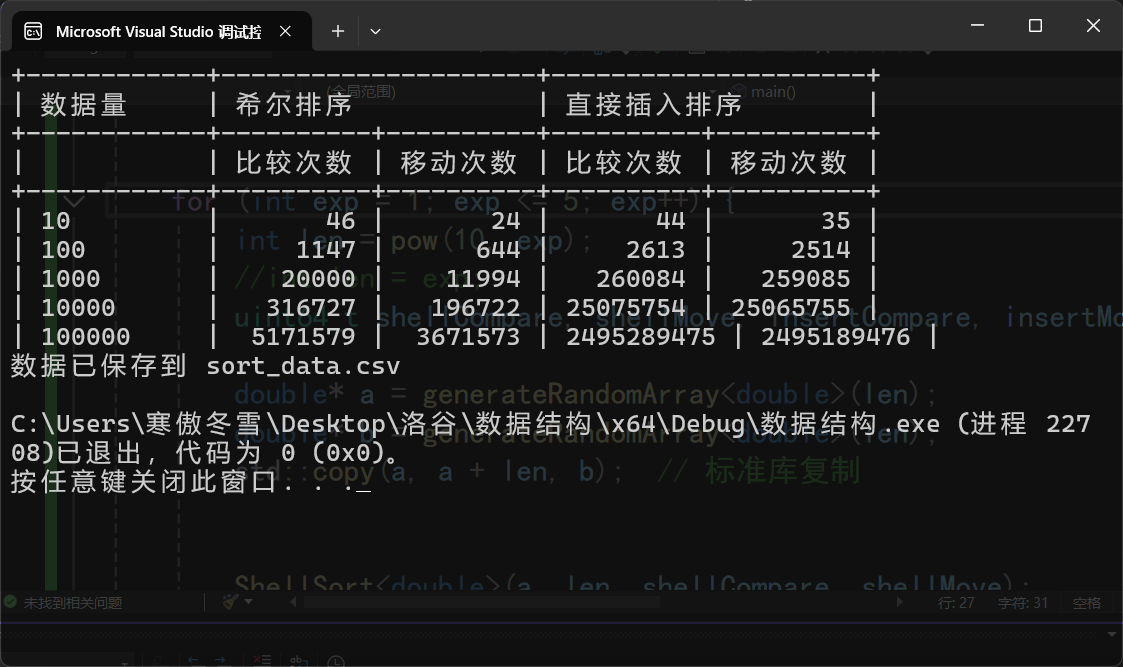
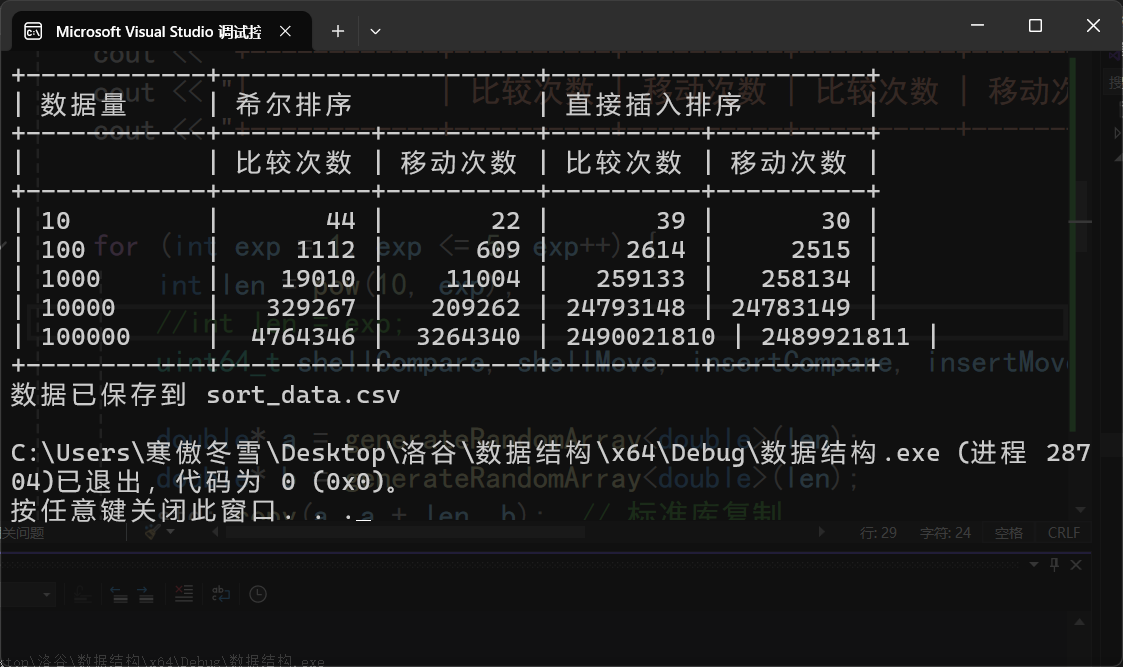
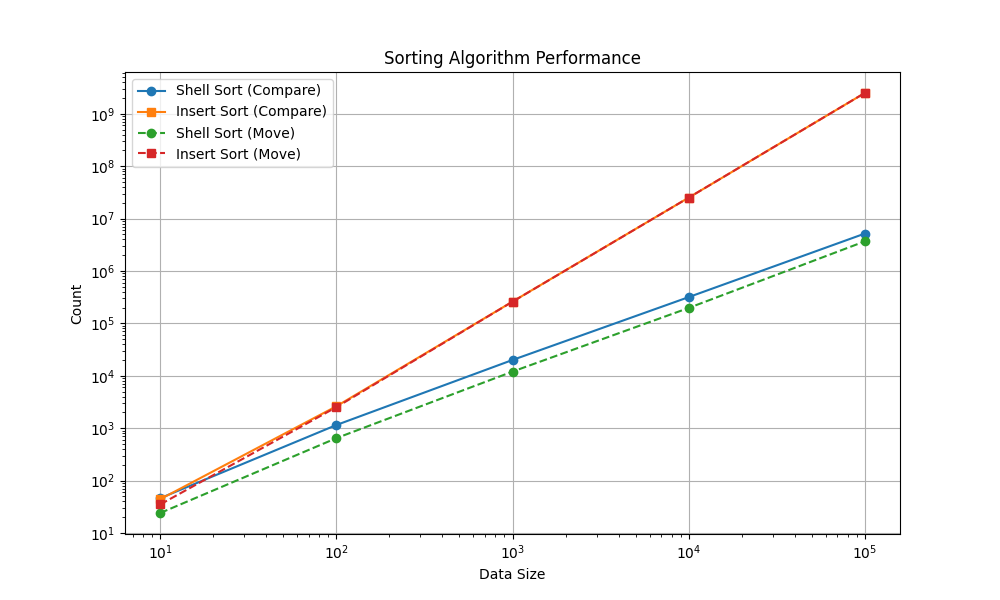
折线图比较:
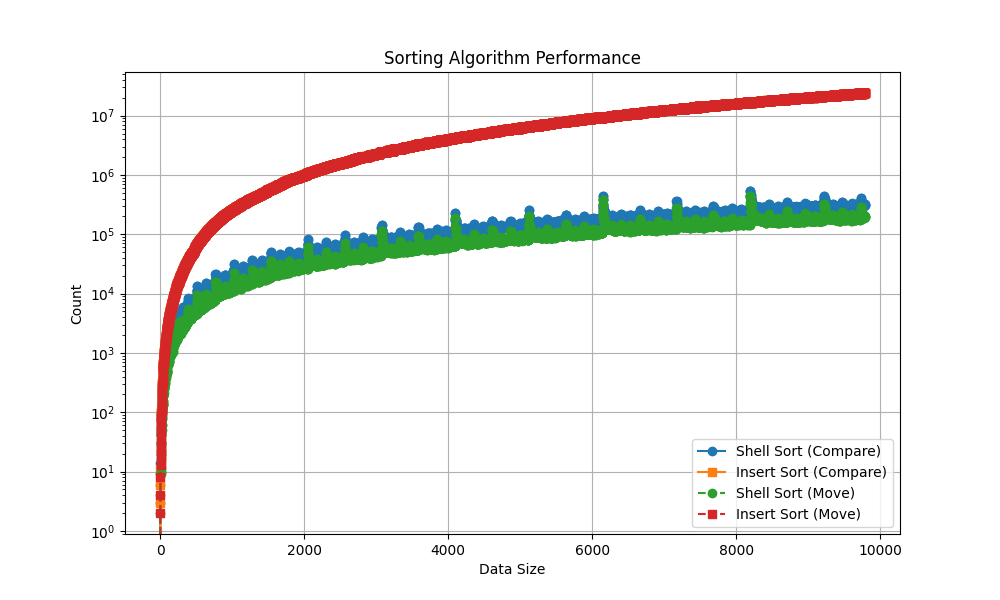
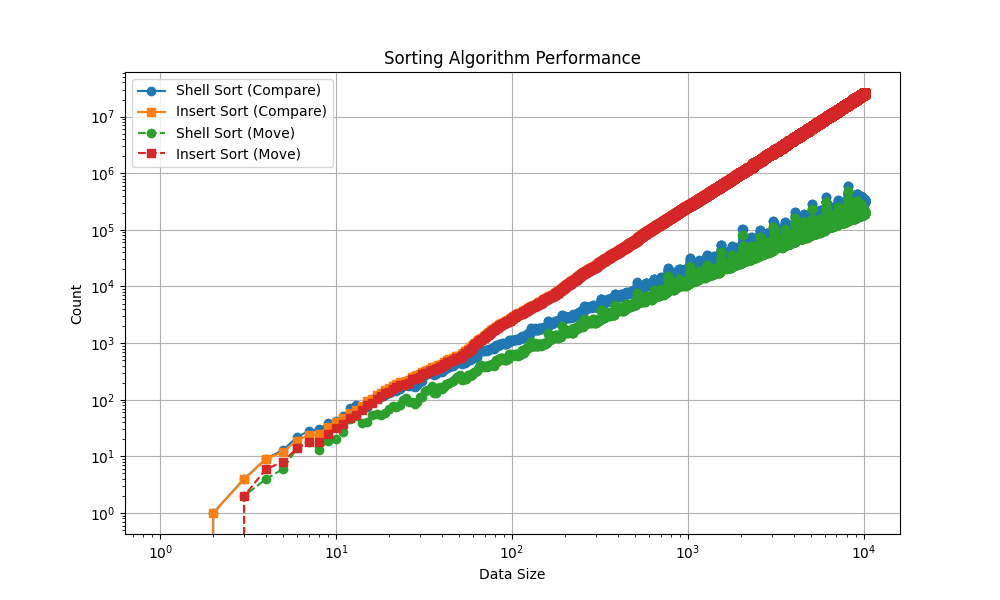
5、结论
以上得到的数据图表格和折线图可以分析得到一下几点结论:
1.在数据较多时,两终算法的比较次数和移动次数在同一数量级;
2.当数据量较少时(datasize<100),两个算法移动次数和比较次数相差不大;
3.当数据量位于100以内时,有时直接插入优于希尔排序;
4.当数据量大于10^3规模时,希尔排序明显好于直接插入;
5.两种算法比较次数和移动次数随数量级近视线性增长。
由此可见,当数据量较少时,算法之间的差异显现的不明显,在有些情况下两种算法可适用于少量数据,时间上并无明显差别,只有当数据量极大时才能体现算法的优异和差别。
6、讨论到十万级以后,希尔的序列怎么取?
** **十万级数据建议: 使用 Sedgewick增量序列:1, 5, 19, 41, 109, 209, 505, 929... 公式:gap = 9 * 4^i - 9 * 2^i + 1 或 gap = 4^i - 3 * 2^i + 1
1. Sedgewick增量序列的原理
Sedgewick增量序列是由计算机科学家Robert Sedgewick提出的优化方案,通过数学公式生成高效的间隔序列(gap sequence),其核心优势是:
- 减少比较和移动次数:相比原始希尔排序的
gap = n/2,能更快速将元素移动到接近最终位置 - 理论最优:平均时间复杂度可优化至 O(n^(4/3)),最坏情况仍为O(n²)
- 适应大数据量:特别适合10万级及以上数据规模
2. 序列生成公式
Sedgewick提出了两种交替使用的公式:
公式A(奇数项)
gap=9×4i−9×2i+1gap=9×4i−9×2i+1
生成序列:1, 19, 109, 505, 2161...
公式B(偶数项)
gap=4i−3×2i+1gap=4i−3×2i+1
生成序列:5, 41, 209, 929, 3905...
合并后的完整序列
将两个公式生成的序列按升序排列:
1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905...
3.deep seek解答讨论到十万级以后,希尔的序列怎么取?

 浙公网安备 33010602011771号
浙公网安备 33010602011771号