概率与期望

1.一些定义

看看就好，很好理解

随机试验：

• 不能预先确知结果
• 试验之前可以预测所有可能结果或范围
• 可以在相同条件下重复实验

样本空间：随机试验所有可能结果组成的集合
离散样本空间、无穷样本空间

样本空间的任意一个子集称之为事件
所以说事件也可以看成一个集合，那么集合的运算和定律，放在事件上也适用

事件发生：在一次试验中，事件的一个样本点发生
必然事件：样本空间全集
不可能事件：空集

2.概率

概率这里的几个性质可能有用
概率：为样本空间每一个事件定义一个实数，称为概率。事件\(A\)的概率称为\(P[A]\)

• \(P(A)\geq 0\)
• \(\sum P(A)=1\)
• 若\(A_1,A_2,\dots\)两两不相容，也就是对于任意\(i,j,A_i\cap A_j=\emptyset\)，则\(P(A_1\cup A_2 \cup\dots)=P(A_1)+P(A_2)+\dots\)
• \(P(B-A)=P(B)-P(AB)\)，\(P(AB)\)即为\(AB\)同时发生的概率，相当于\(B\)的一个子集
• \(0\leq P(A) 1\)
• \(P(A\cup B)=P(A)+P(B)-P(AB)\)，本质上就是一个容斥原理

3.条件概率

\(P(A\mid B)=\dfrac{P(AB)}{P(B)}\)，表示\(B\)发生时，\(A\)发生的概率

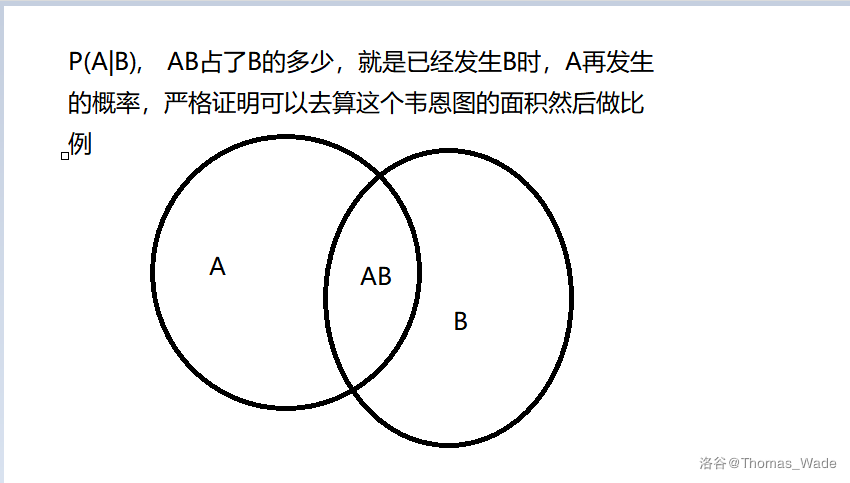
然后把分母一乘就是\(P(AB)=P(A\mid B)P(B)\)

• \(P(\emptyset \mid A)=0\)
• 还是如果\(B_1,B_2,\dots\)互不相容，\(P(B_1\cup B_2\cup\dots)\mid A=\sum_{i=1}^{n}P(B_i\mid A)\)，画个韦恩图很好理解
• \(P(\complement B\mid A)=1-P(B|A)\)，这个也很显然
• \(P(B\cup C\mid A)-P(B\mid A)+P(C\mid A)-P(BC\mid A)\)
  

独立事件：
这个要用到条件概率，所以放在这了
若\(P(AB)=P(A)P(B)\)，那么\(AB\)独立
\(AB\)独立：

\[P(B\mid A)=\frac{P(AB)}{P(A)}=\frac{P(A)P(B)}{P(A)}=P(B) \]

也可以理解为，若\(AB\)独立，则\(A\)是否发生，与\(B\)是否发生无关
不可能事件，必然事件，和任何事件都是独立事件

4.期望

期望实际上是建立在一个函数上
是对所有情况的概率乘以当前情况的权值求和的结果，这个权值和概率无关

期望的和=和的期望

5.贝叶斯公式

设\(B_1,B_2,\dots,B_n\)为一个样本空间的划分，\(A\)是任意事件，则：

\[P(B_i\mid A)=\dfrac{P(A\mid B_i)P(B_i)}{\sum_{j=1}^n P(A\mid B_j)P(B_j)} \]

证明，考虑等号右边
对分子变形，运用刚才条件概率那个变形以后的式子：

\[P(A\mid B_i)P(B_i)=P(AB_i) \]

又因为\(B_1,B_2,\dots,B_n\)是对样本空间的划分，也就是不会有一个\(A\)的子集和任意一个\(B\)都没有交集，所以对分母：

\[\sum_{j=1}^n P(A\mid B_j)P(B_j)=\sum_{j=1}^n P(AB_j)=P(A) \]

那么原式就等于：

\[\frac{P(AB_i)}{P(A)}=P(B_i\mid A) \]

那么得证
其中，对分母做变形的结果，叫做全概率公式

比如说这样一个例子，摘自百度百科

因此，\(B_i\)一般视为导致实验结果\(A\)的原因，\(P(B_i)\)就是各种原因的发生可能性大小，称为先验概率
\(P(B_i\mid A)\)反应的是，当结果\(A\)发生后，再对各种原因概率的新认识，称为后验概率
这就是一些很复杂的东西了，更为具体的就从那两个链接点进去看吧

6.概率与期望dp

这的确是个烦人的东西

关于期望dp为什么要逆推而顺推不行

对于期望dp，一般使用逆推，这一点就很迷惑
以P2473 [SCOI2008]奖励关一题为例
这个题用状压dp没什么好说的，\(f_{i,t}\)表示的是当前第\(i\)次抛出物品，已经选了的物品集合为\(t\)的最优期望得分
尝试写出顺推的转移方程，\(j\)是当前枚举到的物品：
如果\(j\)可以选：

\[f_{i,t}+a_j\rightarrow f_{i+1,t|2^{j-1}} \]

如果\(j\)不能选：

\[f_{i,t}\rightarrow f_{i+1,t} \]

如果顺推，考虑\(f_{i,t}\)这样一个状态，它可以转移到\(f_{i+1,t|2^{j-1}}\)，这是选了第\(j\)个的情况
当然如果没选它也可以转移到另一个状态，这里只是举着一个例子，另一种转移到的状态就不讨论了
但是这个转移到的状态(\(f_{i+1,t|2^{j-1}}\))，由于\(f_{i,t'}\)中还有好多能通过上面说的两种转移方法使\(f_{i,t'}\rightarrow f_{i,t}\)
所以这个状态还可以通过其它一堆状态转移而来，十分混乱
那么也就并不能只通过最后除以\(n\)来得到期望

那为什么逆推是可以的呢？

if((t&s[j])==s[j]){
	f[i][t]+=std::max(f[i+1][t],f[i+1][t|(1<<(j-1))]+a[j]);
}
else f[i][t]+=f[i+1][t];

看这样一段逆推的代码，是从我下面给出的AC代码中摘出来的
显而易见，\(f_{i,t}\)只能由一种情况转移而来，就可以用除以\(n\)来算期望了

另外，@天泽龟大佬的这段话也可以结合着体会一下

个人理解是：因为一个状态到后面状态的可能性是均分的（1/n1/n），但是由从其他状态导入后一个状态时，由于题目条件的约束，其他状态的各个概率并不是均分的。而且这题的条件约束是个乱七八糟的集合，毫无规律，所以正推不了。

给出我的AC代码

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<iomanip>
#include<cstring>
#define reg register
#define EN std::puts("")
#define LL long long
inline int read(){
	int x=0,y=1;
	char c=std::getchar();
	while(c<'0'||c>'9'){if(c=='-') y=0;c=std::getchar();}
	while(c>='0'&&c<='9'){x=x*10+(c^48);c=std::getchar();}
	return y?x:-x;
}
int n,k;
int s[20];
double f[106][35000];
int a[20];
inline void max(double a,double b){(a<b)&&(a=b);}
int main(){
	k=read();n=read();
	for(reg int x,i=1;i<=n;i++){
		a[i]=read();
		while(x=read()){
			s[i]|=(1<<(x-1));
		}
	}
	reg int lim=1<<n;
	for(reg int i=k;i;i--){
		for(reg int t=0;t<lim;t++){
			for(reg int j=1;j<=n;j++){
				if((t&s[j])==s[j]){
					f[i][t]+=std::max(f[i+1][t],f[i+1][t|(1<<(j-1))]+a[j]);
				}
				else f[i][t]+=f[i+1][t];
			}
			f[i][t]/=n;
		}
	}
	std::printf("%.6lf",f[1][0]);
	return 0;
}