计算机体系结构01之原码与补码

计算机体系结构之01之原码与补码

这一篇用来讲计算机中的原码与补码。

目录

• 计算机体系结构之01之原码与补码
  • 1 计算机采用二进制的原因
  • 2 R进制及加权和
    • 2.1 R进制数
    • 2.2 R进制数的按权展开的加权和
  • 3 有符号数的表示法：原码与补码
    • 3.1 原码
    • 3.2 补码
    • 3.3 原码转补码
    • 3.4 补码转原码
    • 3.5 原码补码转换工具
    • 3.6 补码计算的溢出规则

提供原码补码转换工具：

https://surez-ok.github.io/toolkit/Complement2Origin/

原码补码转换工具界面如下图所示（使用示例可点击？按钮）：

1 计算机采用二进制的原因

计算机是采用二进制进行编码的，主要原因如下：

1. 技术实现简单：二进制有两种基本状态（0和1），在物理层面，这可以对应于电路的两种状态，比如开/关、高电压/低电压等。这种简单的二元状态非常容易通过电子元件如晶体管来实现，使得硬件设计变得相对简单且成本较低；
2. 可靠性高：由于二进制系统只有两种状态，在实际的物理存储和传输过程中更容易区分这两个值，从而减少了出错的可能性。相比之下，如果使用更多的数值（例如十进制），则需要更复杂的电路设计，并且随着状态数量的增加，出错的概率也会增加；
3. 计算逻辑简单：基于二进制的算术运算规则比较简单，加法、减法、乘法和除法等基本运算都可以通过一系列固定的逻辑操作完成。这些逻辑操作易于用硬件电路实现。

2 R进制及加权和

2.1 R进制数

二进制同人们日常使用的十进制原理是相同的，区别是两者的基数不同。

一般的，任意一个R进制数（R是正整数）

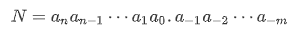
其中：

• R 表示基数（如二进制 R=2，十进制 R=10，十六进制 R=16）
• ai：每一位上的数码（digit），取值范围为 0 ≤ ai < R
• 整数部分有 n+1 位，小数部分有 m 位

2.2 R进制数的按权展开的加权和

R 进制数可以写成如下 按权展开的加权和 形式：

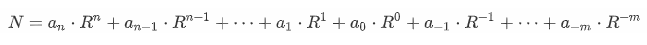
或者用求和符号简洁地表示为：

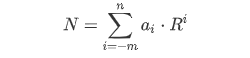
注意：按权展开的加权和主要用于将任意进制转换为十进制

举例如下，将二进制数 101.11B 转十进制：

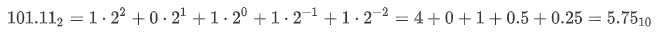
3 有符号数的表示法：原码与补码

上述讨论的R进制数只是纯数值的表示形式，本身并不直接涉及符号，而计算机需要表示有符号数，如（+5，-10 等），所以有两种解决思路：原码与补码。

下面讨论的都是有符号数，无符号数不涉及原码与补码

3.1 原码

原码（Sign-Magnitude Representation）：采用“符号-数值”的表示形式，在这种表示法中，最高位（MSB, Most Significant Bit）用来表示符号（0 表示正数，1 表示负数），其余位用来表示数值部分。

对于形式如下的原码

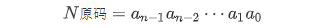
其表示的值为：

原码有两个优点：

1. 原码直观易懂，对于人类来说，原码非常直观。例如，8 位二进制原码 00000101 表示真实值 +5，而 10000101 表示真实值 -5;
2. 原码实现乘除运算比较简单直接，必须首先检查操作数的符号，然后根据符号执行相应的操作（如将减法转换为加法）。这增加了运算的复杂性和硬件实现的成本。

但原码也存在两个缺点：

1. 存在两个0，一个+0和一个-0，这有悖与人类的习惯，使用也不方便
2. 原码的加减运算规则复杂，这对于逻辑的实现影响很大

权衡上述利弊，现代计算机中基本不使用原码来表示整数，而是使用补码。

3.2 补码

补码时有符号数的另一种表示方法，补码最大的优点是：可以用加法来完成减法运算，实现加减法的统一。

对于形式如下的补码：

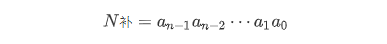
其表示的值为：

先来看看补码时怎么实现加减法统一的？

举例：

8位有符号运算：5 - 3 可转换为 5 + （256 - 3) ，其中 （256 - 3) 正好是-3 的补码，这样变换后就可以将减法变为加法了。

这样在计算机中不用把加法器和减法器分开了，只需要加法器就可以实现减法和加法。

这个例子有一个问题，5 - 3 = 5 + （256 - 3) 并不相等啊，这样处理没有问题，因为位数是8位的，超过8位的高位会自动舍弃。

3.3 原码转补码

一般方法总是喜欢引入反码来计算补码，但其实反码仅仅是个中间产物，我们也可以绕过反码来计算补码

原码转补码公式：

对于n位原码（即1位符号位和n-1位数值位），转为补码采用如下公式：

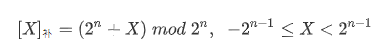
原码转补码采用的方法：

方法1： 直接采用上述公式计算

方法2：当最高位为0时，补码与原码相同，当最高位为1时，原码的高位不变，其余位取反后末尾加1

举例如下：

正数转补码

8位有符号数+3 转为补码，其8位原码为0b00000011

采用方法1，补码为( 0b100000000+0b00000011)然后取模 = (0b100000011)然后取模 = 0b00000011

采用方法2，最高位为0，补码与原码相同，为0b00000011

负数转补码：

8位有符号数-3 转为补码，-3的8位原码为0b10000011

采用方法1，补码为(0b100000000 - 0b00000011 ) 然后取模 = 0b11111101

采用方法2，最高位为1，则其补码为反码加1，反码（符号位不变，其余位取反）为0b11111100，加1后得到补码为0b11111101

3.4 补码转原码

补码的补码即原码，针对补码再求一次补码，得到原码。

我们采用上面提到的求补码方法。

举例如下：

其8位补码为0b00000011，求其原码

采用方法1，求补码后，(0b1000000000 + b00000011 ) 然后取模 = (0b100000011)然后取模 = 0b00000011，即原码

采用方法2，最高位为0，补码为0b00000011，即原码

8位补码为0b11111101，求其原码

采用方法1，对其求补码，(0b100000000 - 0b01111101 )=0b10000011 即原码

采用方法2，对其求补码，0b11111101 其补码为反码加1，反码（符号位不变，其余位取反）为0b10000010，加1后得到补码为0b10000011

3.5 原码补码转换工具

3.3与3.4节讲了原码转补码以及补码转原码的方法，我们也可以自制小工具来解决这个问题。

https://surez-ok.github.io/toolkit/Complement2Origin/

原码补码转换工具界面如下所示：

其中：

1. 原码与补码只支持10进制与16进制，16进制需要以0x或0X作为前缀
2. 原码框与补码框都可以作为输入，另一框作为转换结果

其它使用示例可点击工具右上方的问号？按钮

3.6 补码计算的溢出规则

上面讲到：计算机科学一般使用补码来参与有符号数的运算，使用补码运算时候可能存在溢出。

这里仅提一下发生溢出的场景：

发生溢出的情况为：如果两个补码的符号位相同，但结果的符号位与操作数的符号位不同，则发生了溢出。具体来说：如果符号位没有进位而次高位有进位，或者符号位有进位而次高位没有进位，则发生了溢出。

可总结为：符号位的进位（Cf）与次高位的进位（Cn-1）不同时发生溢出。

参考：

1. 《计算机体系结构基础》