栅格距离~~~

曼哈顿距离：

出租车距离，在一个横竖分布的网格上，两点之间的距离即为曼哈顿距离，只能横着走或者竖着走

切比雪夫距离：

棋盘距离，在一个国际棋盘上，王从一点到另一点的距离，王可以向周围八个方向走，显然最优决策是先不断斜着靠近，再横着或者竖着达到目标点

欧式距离又称欧几里得距离或欧几里得度量（Euclidean Metric），以空间为基准的两点之间最短距离

 

摘自http://www.cnblogs.com/hadilo/p/5970408.html

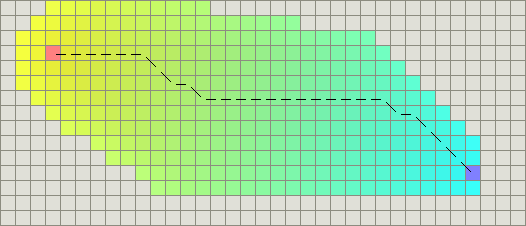
Manhattan distance#

 

The standard heuristic for a square grid is the Manhattan distance. Look at your cost function and find the minimum cost D for moving from one space to an adjacent space. In the simple case, you can set D to be 1. The heuristic on a square grid where you can move in 4 directions should be D times the Manhattan distance:

 

function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * (dx + dy)

 

How do you pick D? Use a scale that matches your cost function. For the best paths, and an “admissible” heuristic, set D to the lowest cost between adjacent squares. In the absence of obstacles, and on terrain that has the minimum movement cost D, moving one step closer to the goal should increase g by D and decrease h by D. When you add the two, f (which is set to g + h) will stay the same; that’s a sign that the heuristic and cost function scales match. You can also give up optimal paths to make A* run faster by increasing D, or by decreasing the ratio between the lowest and highest edge costs.

 

 

(Note: the above image has a tie-breaker added to the heuristic.)

 

Diagonal distance#

 

If your map allows diagonal movement you need a different heuristic. The Manhattan distance for (4 east, 4 north) will be 8⨉D. However, you could simply move (4 northeast) instead, so the heuristic should be 4⨉D2, where D2 is the cost of moving diagonally.

 

 

function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * (dx + dy) + (D2 - 2 * D) * min(dx, dy)

 

Here we compute the number of steps you take if you can’t take a diagonal, then subtract the steps you save by using the diagonal. There are min(dx, dy) diagonal steps, and each one costs D2 but saves you 2⨉D non-diagonal steps.

 

When D = 1 and D2 = 1, this is called the Chebyshev distance. When D = 1 and D2 = sqrt(2), this is called the octile distance.

 

Another way to write this is D * max(dx, dy) + (D2-1) * min(dx, dy). Patrick Lester writes it yet a different way, with if (dx > dy) (D * (dx-dy) + D2 * dy) else (D * (dy-dx) + D2 * dx). These are all equivalent.

 

Euclidean distance#

 

If your units can move at any angle (instead of grid directions), then you should probably use a straight line distance:

 

function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * sqrt(dx * dx + dy * dy)

 

However, if this is the case, then you may have trouble with using A* directly because the cost function g will not match the heuristic function h. Since Euclidean distance is shorter than Manhattan or diagonal distance, you will still get shortest paths, but A* will take longer to run:

 

 

http://theory.stanford.edu/~amitp/GameProgramming/Heuristics.html