数据结构与算法——十个排序算法之四 · 希尔排序

十个排序算法之三的插入排序虽好,但是某些特殊情况也有很多缺点,比如像下面这种情况:

156

161

163

165

167

168

169

1

2

 

 

169 前的元素基本不用插入操作就已经有序, 元素 1 和 2 的排序几乎要移动数组前面的所有元素。 由此需要了解一下希尔排序!

 

1. 希尔排序介绍

希尔排序是希尔（Donald Shell）于 1959 年提出的一种排序算法。希尔排序也是一种插入排 序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序。它与插入排序 的不同之处在于，它会优先比较距离较远的元素。

希尔排序是把记录按下表的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐 渐减少，每组包含的元素越来越多，当增量减至 1 时，所有元素被分成一组,实际上等同于执行一 次上面讲过的插入排序，算法便终止。

 

2. 适用说明

希尔排序时间复杂度是 O(n^(1.3-2))，空间复杂度为常数阶 O(1)。希尔排序没有时间复杂度为 O(n(logn)) 的快速排序算法快 ，因此对中等大小规模表现良好，但对规模非常大的数据排序不是最优选择，总之比一般 O(n^2 ) 复杂度的算法快得多。

 

3. 基本步骤

选择增量 ：gap=length/2，缩小增量：gap = gap/2 增量序列：用序列表示增量选择，{n/2, (n/2)/2, …, 1} 先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述： 选择一个增量序列 t1，t2，…，tk，其中 ti>tj，tk=1； 按增量序列个数 k，对序列进行 k 趟排序； 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进 行直接插入排序; 仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

 

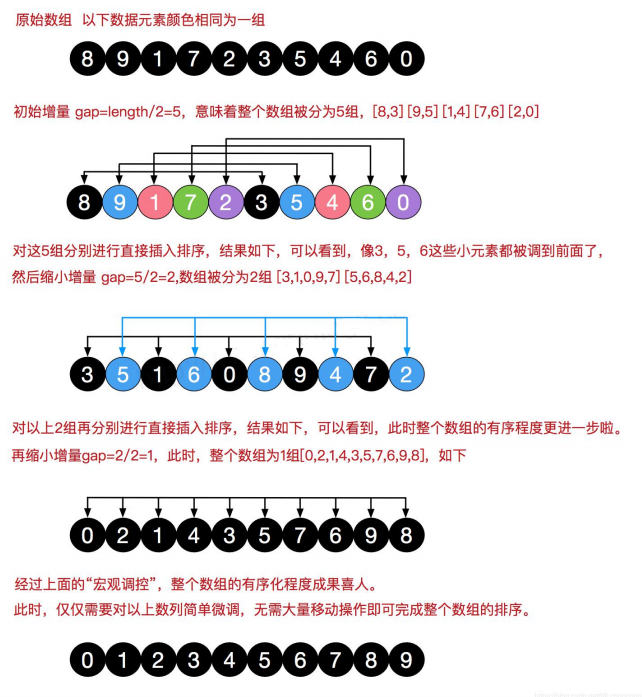
4.过程演示

希尔排序目的为了加快速度改进了插入排序，交换不相邻的元素对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。在此我们选择增量 gap=length/2，缩小增量以 gap = gap/2 的方式，用序列 {n/2,(n/2)/2...1} 来表示。

 

示例：

 

动图演示（来源 runoob.com）：

 

 

代码实现：

#include <stdio.h>
#include <stdlib.h>

void ShellSort(int arr[], int len)            //希尔排序
{
    int gap = len/2;
    for(; gap > 0; gap=gap/2)
    { //增量，依次按除 2 的范围缩小
        for(int i=gap; i<len; i++)
        {
            int current = arr[i];
            int j = 0;
            for(j=i-gap; j>=0 && arr[j] > current; j-=gap)
            {
                arr[j + gap] = arr[j];
            }
            
            arr[j + gap] = current;
        }
    }
}

int main(void)
{
    int beauties[]={163, 161, 158, 165, 171, 170, 163, 1, 2};
    int len = sizeof(beauties)/sizeof(beauties[0]);
    ShellSort(beauties, len);
    
    printf("排序以后的结果是:\n");
    
    for(int i=0; i<len; i++)
    {
        printf("%d ", beauties[i]);
    }
    
    system("pause");
    
    return 0;
}

 

 

 

 

 

=====================================================================================================================