9.29 模拟赛
前言
业精于勤荒于嬉,行成于思毁于随
正文(模拟赛)
卦象:平
感受:5min 口胡 T1,50min 码完代码,有点唐了。开 T2,有点困,思考良久只会暴力,遂弃。厕所浅住一会后,开 T3,神秘构造,试图切掉,思考半小时后无果,选择 20pts 暴力。最后开 T4,发现很像 dottle 讲的一道原题,所以直接试图莽正解,然而两个小时后依旧不会,只会 \(O(n^2 \log n)\),无奈,不写代码回去写 T2。最后一小时,码 T2 的暴力分数,然而代码各种出锅,最后压哨两分钟调出来。最终成绩 \(100+40+20+0=160\),喜提机房倒数……
T1
简单双指针维护极差
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5,M=4e6+5,INF=2147483647,P=1e9+9;
mt19937 RD(time(NULL));
int n,tot,t[N],sum,tar,rnd[N];
struct node{int x,id;}a[M];
inline int read(){
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-f;
c=getchar();
}
while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
return x*f;
}
inline void write(int x){
if(x>9)write(x/10);
putchar(x%10+'0');
return;
}
inline bool cmp(node s,node t){return s.x<t.x;}
inline void init(){
for(int i=1;i<=n;i++)rnd[i]=(int)(RD()%P);
for(int i=1;i<=n;i++)tar^=rnd[i];
return;
}
inline void upd(node o){
if(t[o.id]==0)sum^=rnd[o.id];
t[o.id]++;
return;
}
inline void del(node o){
if(t[o.id]==1)sum^=rnd[o.id];
t[o.id]--;
return;
}
signed main(){
n=read();
if(n==1){puts("0");return 0;}
init();
for(int i=1,k;i<=n;i++){
k=read();
for(int j=1,x;j<=k;j++){
x=read();
a[++tot]={x,i};
}
}
sort(a+1,a+tot+1,cmp);
int ans=INF;
for(int i=1,j=1;i<=tot;i++){
while(j<=tot&&sum!=tar)upd(a[j++]);
if(sum==tar)ans=min(ans,a[j-1].x-a[i].x);
del(a[i]);
}
write(ans);puts("");
return 0;
}
T2
大分讨,有点破防
考虑新加入一个点对答案的影响,要么无影响,要么在答案上加一,要么会影响子树 swap 的操作
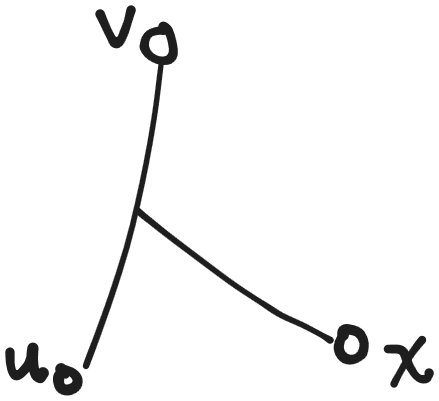
简单抽象出如上三叉结构(其中 \(u \to v\) 是直径,\(x\) 是新加入的点),分讨维护即可
代码上,树上距离以及分讨都需要用到倍增 LCA,剩下的没了
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int id,n,lstans,st,ed,fa[N][19],dep[N];
inline void chkmx(int &x,int y){x=max(x,y);return;}
inline int LCA(int u,int v){
if(dep[u]<dep[v])swap(u,v);
for(int i=18;i>=0;i--)
if(dep[fa[u][i]]>=dep[v])u=fa[u][i];
if(u==v)return u;
for(int i=18;i>=0;i--)
if(fa[u][i]!=fa[v][i])u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
inline int getdis(int u,int v){return dep[u]+dep[v]-dep[LCA(u,v)]*2;}
inline int cal(int nd,int x,int p,int q,int dis){
if(q==x||q==nd)return 0;
int len=dep[nd]-((dep[p]>=dep[q])?dep[p]:dep[q])-1;
return len+dis;
}
inline void work(int x){
for(int i=1;i<=18;i++)fa[x][i]=fa[fa[x][i-1]][i-1];
int len1=getdis(st,ed),len2=getdis(st,x),len3=getdis(ed,x);
int sum=(len1+len2+len3)/2;
int a=sum-len3,b=sum-len2,c=sum-len1,mn=min(min(a,b),c);
if(b==mn&&c>mn)swap(x,ed),lstans++;
else if(a==mn&&c>mn)swap(x,st),lstans++;
chkmx(lstans,getdis(st,ed));
chkmx(lstans,cal(st,x,LCA(st,ed),LCA(st,x),getdis(ed,x)));
chkmx(lstans,cal(ed,x,LCA(st,ed),LCA(ed,x),getdis(st,x)));
return;
}
inline void init(){
st=ed=1;fa[1][0]=0;dep[1]=1;lstans=0;
return;
}
int main(){
// freopen("forest.in","r",stdin);
// freopen("forest.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>id>>n;init();
for(int i=2;i<=n;i++){
int f;cin>>f;f^=lstans;
fa[i][0]=f;dep[i]=dep[f]+1;
work(i);
cout<<lstans<<'\n';
}
return 0;
}
T3
神秘构造题
钦定循环移位周期为 \(x\),则容易做到在有限次数内使得 \([x+1,n]\) 归位
对于前 \(x\) 个元素,我们希望能做到邻项交换,使得修改其循环移位的顺序,进一步地,我们希望在不影响其它元素的情况下交换 \(p_1,p_2\)
当 \(x\) 为偶数时,注意到可以由如下构造方式完成邻项交换操作
\([2,x+1]\) 一次,随后 \([2,x+1]\) 与 \([1,x]\) 交替进行共计 \(x\) 次
如何思考到这个结论无从得知,可能需要强大的拍脑袋能力。而正确性相当有保证,可以手玩
现在我们 level-up,完成 \(p_1\) 与 \(p_i\) 的交换操作,容易想到先把 \(p_i\) 移位到下标 \(2\) 的位置,套用上述邻项交换之后,再还原即可
因此,我们也可以按 \(1 \to x\) 的顺序使其依次归位
上述构造一定是有正确性保证的,而操作次数也有讲究,具体地,期望操作次数可以被刻画为如下公式
由后面这一项,\(x\) 的上界不应该超过 \(\sqrt{m}\),所以直接枚举 \(x=2,4 \dots\) 确定最优的 \(x\)
事实上,取 \(x=\frac{2}{3} \sqrt{n}\) 可以草过去
剩下的就是直接模拟实现了……
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e4+5,M=2e6+5;
int n,x,a[N],res[M],ans;
inline void upd(int l){
rotate(a+l,a+l+1,a+l+x),res[++ans]=l;
return;
}
int main(){
// freopen("rotate.in","r",stdin);
// freopen("rotate.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;x=(int)(0.666666*sqrt(n));
if(x&1)x++;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=n;i>=x;i--){
int u=find(a+1,a+n+1,i)-a;
while(u+x-1<=i)upd(u),u+=x-1;
if(u==i)continue;
while(u>=i-x+1)upd(i-x+1),u--;
}
for(int i=1;i<=x-1;i++){
int u=find(a+1,a+x,i)-a;
if(u==i)continue;
for(int j=1;j<=u-i-1;j++)upd(i+1);
upd(i+1);
for(int j=1;j<=x;j++)upd(i+(j&1));
for(int j=1;j<=x-(u-i-1);j++)upd(i+1);
}
cout<<x<<' '<<ans<<'\n';
for(int i=1;i<=ans;i++)cout<<1<<' '<<res[i]<<'\n';
return 0;
}
T4
赛时想法与正解的 LCP 是 \(O(n^3)\) 的 DP,就顺着这个思路继续向下延伸
记 \(f_{i,a,b}\) 表示考虑前 \(i\) 个数,上升序列的前缀 \(\max\) 为 \(a\),下降序列的前缀 \(\min\) 为 \(b\) 的最大答案
转移是容易的,可以刷表,一个状态只会对 \(O(1)\) 个状态产生贡献
考虑优化,我们对 \(a,b\) 间的大小关系进行分析
为了方便表述,不妨投射到二维平面上进行刻画,并定义相关记号
定义:\(\operatorname{{LIS}}(i,x)\) 表示以 \([i,n]\) 这一后缀中,首项 \(>x\) 的最长上升子序列长度;\(\operatorname{{LDS}}(i,x)\) 表示以 \([i,n]\) 这一后缀中,首项 \(<x\) 的最长下降子序列长度
若 \(a>b\),考虑新插入的 \(p_i\),应当如下图所示
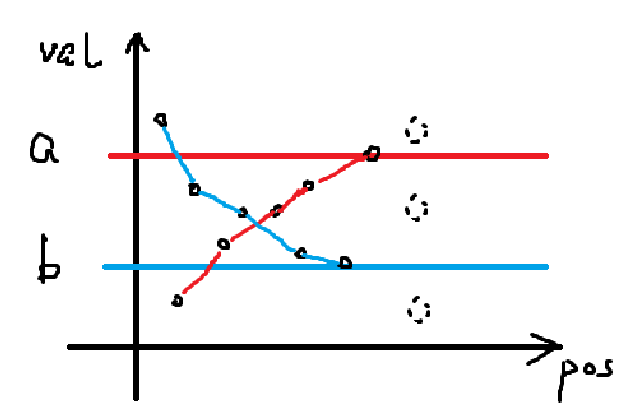
注意到 \(p_i\) 在 \((a,b)\) 间是没有贡献的,而接在上升(或下降)序列后面只会让限制更加严格。因此,当 \(a>b\) 时,容易发现答案就是 \(f_{i,a,b}\) 加上 \(\operatorname{LIS}(i+1,a) + \operatorname{LDS}(i+1,b)\)
而对于 \(a<b\) 的情况,仍旧考虑新插入的 \(p_i\),如下图
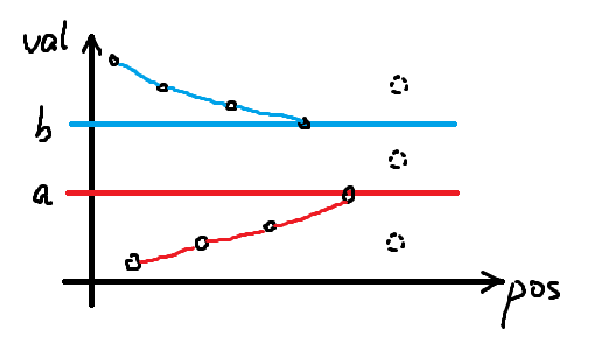
如果 \(p_i\) 在 \(a,b\) 之间,那么 \(f_{i-1,a,b}\) 这个状态会贡献给 \(f_{i,a,p_i}\) 和 \(f_{i,p_i,b}\) 这两个状态。更进一步地,由于前缀 \(\max\) 和前缀 \(\min\) 的性质,所谓的 \(f_{i-1,a,b}\) 一定可以被描述成 \(f_{i-1,pre,nxt}\),其中 \(pre,nxt\) 分别表示 \(p_i\) 在 \(p_{1 \dots i-1}\) 中的前驱与后继
如果 \(p_i\) 满足 \(p_i>b\),分讨其接在哪条序列之后。如果在下降序列之后,显然无贡献,如果接在上升序列之后,相当于 \(f_{i-1,a,b} \to f_{i,p_i,b}\)。转移之后可以转化为 \(a>b\) 的情况,直接用前面 \(\operatorname{LIS} + \operatorname{LDS}\) 的方法贡献答案即可
如果 \(p_i\) 满足 \(p_i<a\),与 \(p_i>b\) 对称,不多赘述
注意到后面的转移本质上只有一维进行改变,不妨搬到线段树上维护,一下子就能做到 \(O(n \log n)\) 的复杂度
如何求 \(\operatorname{LIS}\) 和 \(\operatorname{LDS}\)?以 \(\operatorname{LDS}\) 为例,首项有限制不好做可以考虑倒过来让末项有限制。类似二分求最长上升子序列的思想,当倒序扫描到新元素 \(p_i\) 时,可以先 lower_bound 找到新元素可以影响到的上升子序列,如果钦定元素 \(i\) 为原 \(\operatorname{LDS}\) 的首项的话,它对值域限制的贡献是一段区间,显然可以线段树维护
剩下的就是代码实现上的细节问题了,可能多多少少有点麻烦
点击查看代码
#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define lwbd lower_bound
using namespace std;
const int N=2e5+5;
int n,a[N],b[N],f[N],g[N];pii p1[N],p2[N];
set<int> S;
inline void chkmx(int &x,int y){x=max(x,y);return;}
struct Segment_tree{
struct node{int l,r,mx,tag;}tr[N<<2];
inline void pushup(int u){
tr[u].mx=max(tr[u<<1].mx,tr[u<<1|1].mx);
return;
}
inline void maketag(int u,int v){
tr[u].tag+=v,tr[u].mx+=v;
return;
}
inline void pushdown(int u){
if(!tr[u].tag)return;
int v=tr[u].tag;
maketag(u<<1,v),maketag(u<<1|1,v);
tr[u].tag=0;
return;
}
inline void build(int u,int l,int r){
tr[u].l=l,tr[u].r=r,tr[u].tag=0;
if(l==r){tr[u].mx=0;return;}
int mid=(l+r)>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
return;
}
inline void modify(int u,int ql,int qr,int v){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r){maketag(u,v);return;}
pushdown(u);
int mid=(l+r)>>1;
if(ql<=mid)modify(u<<1,ql,qr,v);
if(qr>mid)modify(u<<1|1,ql,qr,v);
pushup(u);
return;
}
inline int query(int u,int ql,int qr){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r)return tr[u].mx;
pushdown(u);
int mid=(l+r)>>1,res=0;
if(ql<=mid)chkmx(res,query(u<<1,ql,qr));
if(qr>mid)chkmx(res,query(u<<1|1,ql,qr));
return res;
}
}sgt1,sgt2;
inline void initlis(){
for(int i=1;i<=n;i++)b[i]=0;
for(int i=n;i>=1;i--){
int now=lwbd(b+1,b+n+1,-a[i])-b;
p1[i]=mkp(-b[now]+1,a[i]),b[now]=-a[i];
sgt1.modify(1,p1[i].fi,p1[i].se,1);
}
return;
}
inline void initlds(){
for(int i=1;i<=n;i++)b[i]=n+1;
for(int i=n;i>=1;i--){
int now=lwbd(b+1,b+n+1,a[i])-b;
p2[i]=mkp(a[i],b[now]-1),b[now]=a[i];
sgt2.modify(1,p2[i].fi,p2[i].se,1);
}
return;
}
int main(){
// freopen("shung.in","r",stdin);
// freopen("shung.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
sgt1.build(1,1,n),sgt2.build(1,1,n);
initlis(),initlds();
S.insert(0),S.insert(n+1);int ans=0;
for(int i=1;i<=n;i++){
sgt1.modify(1,p1[i].fi,p1[i].se,-1),sgt2.modify(1,p2[i].fi,p2[i].se,-1);
int x=a[i],pre=(*prev(S.lower_bound(a[i]))),nxt=(*S.lower_bound(a[i]));
chkmx(ans,(pre>=1?sgt2.query(1,1,pre):0)+sgt1.query(1,x,x)+1);
chkmx(ans,(nxt<=n?sgt1.query(1,nxt,n):0)+sgt2.query(1,x,x)+1);
if(pre>=1)sgt1.modify(1,pre,pre,1);
if(nxt<=n)sgt2.modify(1,nxt,nxt,1);
f[x]=(pre>=1?f[pre]:0)+1,g[x]=(nxt<=n?g[nxt]:0)+1;
sgt1.modify(1,x,x,f[x]+g[x]-1),sgt2.modify(1,x,x,f[x]+g[x]-1);
S.insert(x);
}
cout<<ans<<'\n';
return 0;
}
好消息:没有挂分
坏消息:rk 5,错估自我能力,策略严重失误
后记
世界孤立我任它奚落
完结撒花!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号