9.23 jsy 随机化选讲
前言
业精于勤荒于嬉,行成于思毁于随
正文(加餐)
随机化选讲,题目有点多,不过完全在可接受范围内
预习的收获颇丰,学到了很多很有意思的《乱搞》,有点期待晚上的授课内容了
A
可重集哈希入门题,随一个键值异或或者求和均可
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
mt19937 RD(time(NULL));
int n,Q,a[N],b[N],s1[N],s2[N];
unordered_map<int,int> mp;
inline bool chk(int l,int r,int L,int R){
if(R-L!=r-l)return false;
return (s1[r]-s1[l-1])==(s2[R]-s2[L-1]);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>Q;
for(int i=1;i<=n;i++){
cin>>a[i];
if(!mp.count(a[i]))mp[a[i]]=RD();
}
for(int i=1;i<=n;i++){
cin>>b[i];
if(!mp.count(b[i]))mp[b[i]]=RD();
}
for(int i=1;i<=n;i++)s1[i]=s1[i-1]+mp[a[i]];
for(int i=1;i<=n;i++)s2[i]=s2[i-1]+mp[b[i]];
while(Q--){
int l,r,L,R;cin>>l>>r>>L>>R;
cout<<(chk(l,r,L,R)?"Yes\n":"No\n");
}
return 0;
}
B
难点在于拍脑袋想到极值分治
注意到当我们钦定最大值之后,区间长度也随之确定,因此用极值分治去维护
假设我们可以 \(O(1)\) 进行区间判断是否为排列,现在确定了区间长度,只需要确定一个区间端点就能做。极值分治惯用技巧,每次只枚举较短的分值区间,容易证明,可能对答案有贡献的区间只有 \(O(n)\) 个
问题转化为,如何 \(O(1)\) 判断一个区间是否为排列
啧,和 A 题找不到差异,随一个键值上去做区间和或者区间异或和即可
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
using namespace std;
const int N=1e6+5;
mt19937 RD(time(NULL));
int n,a[N],s1[N],s2[N],ans;
int stk[N],tp,ls[N],rs[N],rt;bool vis[N];
unordered_map<int,int> mp;
inline void build(){
for(int i=1;i<=n;i++){
int k=tp;
while(k&&a[stk[k]]<a[i])k--;
if(k)rs[stk[k]]=i;
if(k<tp)ls[i]=stk[k+1];
stk[++k]=i,tp=k;
}
return;
}
inline void gethsh(){
for(int i=1;i<=n;i++)mp[i]=RD();
for(int i=1;i<=n;i++)s2[i]=s2[i-1]+mp[i];
for(int i=1;i<=n;i++)s1[i]=s1[i-1]+mp[a[i]];
return;
}
inline bool chk(int l,int r,int L,int R){
if(r-l!=R-L)return false;
return (s1[r]-s1[l-1])==(s2[R]-s2[L-1]);
}
inline void solve(int u,int l,int r){
if(l>r)return;
if(l==r){ans+=(a[l]==1);return;}
int mid=u;
if(ls[u])solve(ls[u],l,mid-1);
if(rs[u])solve(rs[u],mid+1,r);
int len=a[mid];
if(mid-l<=r-mid){
for(int i=l;i<=mid;i++){
int j=i+len-1;
if(j>r)break;
if(j<mid)continue;
ans+=chk(i,j,1,len);
}
}else{
for(int j=r;j>=mid;j--){
int i=j-len+1;
if(i<l)break;
if(i>mid)continue;
ans+=chk(i,j,1,len);
}
}
return;
}
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
gethsh();
build();
for(int i=1;i<=n;i++)vis[ls[i]]=vis[rs[i]]=true;
for(int i=1;i<=n;i++)
if(!vis[i]){rt=i;break;}
solve(rt,1,n);
cout<<ans<<'\n';
return 0;
}
C
完全平方数经典转化:质因子的幂次为偶数
偶数经典转化:异或和为 \(0\)
所以只需要先筛出值域范围内的所有质数,然后再对这些质数随一个键值,那么树上的点的权值就是它质因子分解后的的异或和
考虑维护点到根的路径异或和,记为 \(s_u\),对答案有贡献相当于对 \(s_u=s_v\) 的情况计数,随便做
卡常题都去死
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+5,M=1e4+5;
mt19937 RD(time(NULL));
int n,head[N],tot;ll dis[N];
struct Edge{int to,nxt;ll val;}e[N<<1];
int prime[M],num;bool isprime[M];
unordered_map<int,ll> mp;
unordered_map<ll,int> t;
inline void euler(){
for(int i=1;i<M;i++)isprime[i]=true;
isprime[1]=false;
for(int i=2;i<M;i++){
if(isprime[i])prime[++num]=i;
for(int j=1;j<=num&&i*prime[j]<=n;j++){
isprime[i*prime[j]]=false;
if(i%prime[j]==0)break;
}
}
return;
}
inline ll getkey(int x){
if(mp.count(x))return mp[x];
return mp[x]=RD();
}
inline ll sep(int x){
int res=0;
for(int i=1;i<=num;i++){
if(x<prime[i])break;
if(x%prime[i]==0){
ll w=getkey(prime[i]);
while(x%prime[i]==0)res^=w,x/=prime[i];
}
}
if(x>1)res^=getkey(x);
return res;
}
inline void add(int u,int v,int w){
e[++tot]={v,head[u],w};head[u]=tot;
return;
}
inline void dfs(int u,int fa){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to,w=e[i].val;
if(v==fa)continue;
dis[v]=dis[u]^w;dfs(v,u);
}
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
euler();
cin>>n;
for(int i=1,u,v;i<=n-1;i++){
ll w;cin>>u>>v>>w;w=sep(w);
add(u,v,w),add(v,u,w);
}
dfs(1,0);
for(int i=1;i<=n;i++)t[dis[i]]++;
ll ans=0;
for(auto it=t.begin();it!=t.end();it++){
int c=(it->second);
ans+=(c*(c-1));
}
cout<<ans<<'\n';
return 0;
}
D
我嘞个超绝拍脑袋题,注意到 \(ans \ge n-3\)
这究竟是怎么注意到的
首先,如果 \(k\) 是奇数,就先把它视作为 \(k-1\),转化为 \(k\) 是偶数的情况
不妨设 \(m=\frac{k}{2}\),有
推完式子还有个小尾巴,继续做。\(C^2\) 是完全平方数,不管;如果 \(m\) 是奇数,那么就把一个 \(2!\) 丢出去;对于 \(m!\) ,直接把 \(m!\) 撇了就行
有了下界之后,我们就可以枚举答案,用异或哈希判定其合法性
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
using namespace std;
const int MOD=(1ll<<61)-1ll;
const int N=1e6+5;
mt19937_64 RD(time(NULL));
bool isprime[N];int n,prime[N],tot,f[N];
unordered_map<int,int> mp;
inline void euler(){
for(int i=1;i<N;i++)isprime[i]=true;
isprime[1]=false;
for(int i=2;i<N;i++){
if(isprime[i])prime[++tot]=i,f[i]=RD()%MOD;
for(int j=1;j<=tot&&prime[j]*i<N;j++){
isprime[i*prime[j]]=false;
f[i*prime[j]]=f[i]^f[prime[j]];
if(i%prime[j]==0)break;
}
}
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
euler();
cin>>n;
for(int i=1;i<=n;i++)f[i]^=f[i-1];
int sum=0;
for(int i=1;i<=n;i++)sum^=f[i];
if(sum==0){
cout<<n<<'\n';
for(int i=1;i<=n;i++)cout<<i<<' ';
cout<<'\n';
return 0;
}
for(int i=1;i<=n;i++)
if(sum==f[i]){
cout<<n-1<<'\n';
for(int j=1;j<=n;j++)if(i!=j)cout<<j<<' ';
cout<<'\n';
return 0;
}
for(int i=1;i<=n;i++)mp[f[i]]=i;
for(int i=1;i<=n;i++){
if(mp.count(sum^f[i])&&mp[sum^f[i]]!=i){
int p=mp[sum^f[i]];
cout<<n-2<<'\n';
for(int j=1;j<=n;j++)
if(j!=p&&j!=i)cout<<j<<' ';
cout<<'\n';
return 0;
}
}
cout<<n-3<<'\n';
for(int i=1;i<=n;i++)
if(i!=2&&i!=n&&i!=n/2)cout<<i<<' ';
cout<<'\n';
return 0;
}
E
结论:如果一个区间合法,对于 \(A\) 中任意的某种颜色 \(c_A\),它在 \(A\) 中的出现位置构成的集合 \(S_A\),都会对应一个出现在 \(B\) 中的颜色 \(c_B\),使得它在 \(B\) 中的出现位置构成的集合 \(S_B\) 满足 \(S_A=S_B\)
正确性显然,但想到这个结论很难,需要强大的拍脑袋功力
考虑如何根据上述结论完成者道题目,注意到集合相等,可以哈希
具体地,对于每个位置 \(i\),我们将随机一个权值 \(w_i\)。对于上面的结论,可以概括为由所有集合 \(S_A\) 构成的可重集合,与由所有 \(S_B\) 构成的可重集合,应保证集合相等
可重集合相等,可以想到和哈希或者异或哈希
里面的 \(S_A\) 与 \(S_B\) 判等,依旧是哈希。具体地,对于颜色 \(c_A\),当它出现在 \(i\) 位置的时候,获取 \(f(w_i)\) 的哈希值,对于颜色 \(c_B\),当它出现在 \(i\) 位置的时候,获取 \(-f(w_i)\) 的哈希值。由上,可以发现,\(c_A\) 可以找到在出现位置上一一对应的 \(c_B\),当且仅当哈希值最后为 \(0\)
当然,这边建议令 \(f(x)=x^3\),不容易产生哈希冲突
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=6e5+5,MOD=1e9+9;
mt19937 RD(time(NULL));
int n,m,q,a[N][3],b[N][3];
int w[N],ha[N],hb[N],pos[N],res;
inline int f(int x){return x*x%MOD*x%MOD;}
inline void upda(int x,int v){
for(int j=0;j<3;j++){
int u=a[x][j];
res=(res-f(ha[u])+MOD)%MOD;
ha[u]=(ha[u]+v*w[x])%MOD;
res=(res+f(ha[u]))%MOD;
}
return;
}
inline void updb(int x,int v){
for(int j=0;j<3;j++){
int u=b[x][j];
res=(res+f(hb[u]))%MOD;
hb[u]=(hb[u]+v*w[x])%MOD;
res=(res-f(hb[u])+MOD)%MOD;
}
return;
}
inline void upd(int x,int v){
upda(x,v),updb(x,v);
return;
}
inline void work(){
for(int i=1;i<=n;i++)w[i]=RD()%MOD;
for(int i=1,j=0;i<=n;i++){
while(j<=n&&!res)upd(++j,1);
pos[i]=j-1;upd(i,-1);
}
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m>>q;
for(int i=1;i<=n;i++)
for(int j=0;j<3;j++)cin>>a[i][j];
for(int i=1;i<=n;i++)
for(int j=0;j<3;j++)cin>>b[i][j];
work();
while(q--){
int l,r;cin>>l>>r;
cout<<((pos[l]>=r)?"Yes\n":"No\n");
}
return 0;
}
F
不可以,总司令
简化题意:
\(n\) 点 \(m\) 边有向图,\(q\) 次操作,每次操作形如
-
失活某条边
-
失活某个结点的所有入边
-
激活某条边
-
激活某个结点的所有入边
每次操作时候,判断每个点是否都恰好有一条出边
维护出边,直接模拟,可以获得对应的暴力分数。发现时间复杂度瓶颈在于操作 \(2\) 和操作 \(4\),而维护入边情况上述两种操作都可以 \(O(1)\) 解决,思考如何维护答案
给出一个答案的必要条件 \(入度和=出度和=n\),但这远远不够
注意到对于结点 \(u\),指向结点 \(u\) 的所有点构成的点集 \(S_u\) 是好做的;而如果每个结点恰好有一条出边,那么这些 \(S_u\) 的可重集并应当恰好是全集(因为每个点只有一条出边,所以只会贡献给唯一三 \(S_u\) 恰好一次)
可重集?并?想到哈希,直接维护维护完了,代码不超过 \(30\) 行
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+5;
mt19937 RD(time(NULL));
int n,m,q,in[N],all[N],w[N];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)w[i]=RD();
int sum=0;
for(int i=1;i<=n;i++)sum+=w[i];
int now=0;
for(int i=1;i<=m;i++){
int u,v;cin>>u>>v;
in[v]+=w[u],all[v]=in[v],now+=w[u];
}
cin>>q;
while(q--){
int opt,u,v;cin>>opt;
if(opt==1){cin>>u>>v;in[v]-=w[u];now-=w[u];}
else if(opt==2){cin>>u;now-=in[u];in[u]=0;}
else if(opt==3){cin>>u>>v;in[v]+=w[u];now+=w[u];}
else if(opt==4){cin>>u;now+=(all[u]-in[u]);in[u]=all[u];}
cout<<(now==sum?"YES\n":"NO\n");
}
return 0;
}
G
留坑待填
H
真·随机化
先把所有点随机重排,然后每次维护前缀的答案 \(d\)
比较核心的思想是,把平面按 \(d \times d\) 正方形分块
考虑新插入第 \(i\) 个点,如果它对答案没贡献就跳过,否则它一定对答案有贡献(废话)
有贡献的必要条件一定满足,第 \(i\) 个点所在块的周边的 \(3 \times 3\) 的块是有点的
也就是说,我们只需要枚举周边 \(3 \times 3\) 的块内的点,而由于是按最短距离 \(d\) 分块,所以一个块中最多有 \(O(1)\) 个点,所以直接枚举即可
那么,如果新插入这个点 \(i\) 可以更新答案,那么我们需要重建块状结构
根据随机重排的性质,一个点成为前缀最小值的概率是 \(\frac{1}{i}\),而重建所影响到的点就是 \(i\)。因此,这个算法的总时间复杂度是 \(O(\sum i \times \frac{1}{i})\),即期望线性的
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define db long double
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define vi vector<int>
#define vp vector<pii>
#define pb emplace_back
using namespace std;
const int N=2e5+5;const db INF=4e18;
mt19937 RD(time(NULL));
int n,m;pii a[N];db ans=INF;
unordered_map<int,bool> vis;
unordered_map<int,vp> mp;
inline int geth(int x,int y){return x*(1<<31)+y;}
inline bool check(){
for(int i=1;i<=n;i++){
int x=a[i].fi,y=a[i].se;
if(vis[geth(x,y)])return true;
vis[geth(x,y)]=true;
}
return false;
}
inline db cal(pii s,pii t){
return sqrtl((s.fi-t.fi)*(s.fi-t.fi)+(s.se-t.se)*(s.se-t.se));
}
inline void init(){
for(int i=1;i<=m;i++)
for(int j=i+1;j<=m;j++)
ans=min(ans,cal(a[i],a[j]));
return;
}
inline void rebuild(int m){
mp.clear();
for(int i=1;i<=m;i++){
int x=a[i].fi,y=a[i].se;
int s=floor(x/ceil(ans)),t=floor(y/ceil(ans));
mp[geth(s,t)].pb(mkp(x,y));
}
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;m=max(2ll,(int)(sqrt(n)));
for(int i=1;i<=n;i++)cin>>a[i].fi>>a[i].se;
if(check()){cout<<fixed<<setprecision(4)<<0.0<<'\n';return 0;}
shuffle(a+1,a+n+1,RD);
init();rebuild(m);
for(int i=m+1;i<=n;i++){
int x=a[i].fi,y=a[i].se;
int s=floor(x/ceil(ans)),t=floor(y/ceil(ans));
db res=ans;
for(int ns=s-1;ns<=s+1;ns++){
for(int nt=t-1;nt<=t+1;nt++){
if(!mp.count(geth(ns,nt)))continue;
for(pii o:mp[geth(ns,nt)])res=min(res,cal(a[i],o));
}
}
if(res<ans)ans=res,rebuild(i);
else mp[geth(s,t)].pb(a[i]);
}
cout<<fixed<<setprecision(4)<<ans<<'\n';
return 0;
}
不理解为什么跑不过加强加强版,期望线性还不如双 \(\log\),棒棒糖
I
一个很牛的转化,就是把两个集合的问题捏到一个集合里面,具体操作是把 \(B\) 集合中的所有物品的重量取反(至于怎么想到的?可能看到最大化的东西具有交换律,然后限制条件也只是一个相等关系,所以可能拍一下脑袋就想到了?)
问题转化为了一个经典的 \(01\) 背包问题,然而你发现物品数量是 \(n+m\),背包容量是 \((n+m)\max\{w_i\}\),然后就倒闭了
但是有奇技淫巧之随机重排,随机重排后注意到期望背包容量大概是 \(\sqrt{n} \max \{ w_i \}\) 范围的,然后就可做了
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define vn vector<NODE>
#define pb push_back
using namespace std;
const int N=2e3+5,B=1e5+5,INF=4e18;
mt19937 RD(time(NULL));
int n,m,f[B];
struct NODE{int w,v;};
vn a;
inline void solve(){
a.clear();
cin>>n>>m;
for(int i=1,w,v;i<=n;i++)cin>>w>>v,a.pb({w,v});
for(int i=1,w,v;i<=m;i++)cin>>w>>v,a.pb({-w,v});
shuffle(a.begin(),a.end(),RD);
memset(f,-0x3f,sizeof(f));
int mid=40000;f[mid]=0;
for(int i=0;i<n+m;i++){
if(a[i].w>0){
for(int j=2*mid;j>=a[i].w;j--)f[j]=max(f[j],f[j-a[i].w]+a[i].v);
}else{
for(int j=0;j<=2*mid;j++)f[j]=max(f[j],f[j-a[i].w]+a[i].v);
}
}
cout<<f[mid]<<'\n';
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int T;cin>>T;while(T--)solve();
return 0;
}
J
考虑弱化版,思考长度为 \(2\) 的链如何去做
记 \(f_{u,0/1}\) 表示 \(u\) 子树内,要求有一条贯穿 \(u\) 且长度为 \(0/1\) 的链的答案
这个东西似乎没什么脑子,注意到我们并不关心拼接操作之间的具体匹配关系,我们只需要让它们匹配即可。不难想到记一个辅助数组 \(g_{now,0/1}\),表示考虑 \(u\) 的前 \(now\) 个儿子,长度为 \(1\) 的路径数目奇偶性为 \(0/1\) 时的答案
子树合并的方式转移 \(g\),再用转移出来的 \(g\) 去转移 \(f\),这很对劲
现在来 level-up,思考长度为 \(4\) 的情况
注意到在长度为 \(4\) 的条件下,在 \(u\) 处合并有了更多可能,包括 \(1,3\) 合并与 \(2,2\) 合并
\(2,2\) 合并完全可以类比弱化版的 \(1,1\) 合并,简单在 \(g\) 数组上记录奇偶性即可;\(1,3\) 合并也比较朴素,维护这些链的个数差,不妨多在 \(g\) 上记录一维
重述 \(g\) 的定义,记 \(g_{now,i,0/1}\) 表示考虑前 \(now\) 个儿子,\(1\) 比 \(3\) 多 \(i\) 个,\(2\) 的奇偶性为 \(0/1\) 的最优答案
先不说 \(g\) 的内部转移,先来思考 \(g \to f\) 的转移(即现在 \(u\) 的所有儿子都已经合并,\(g\) 现在集体贡献给 \(f\)),根据 \(0/1/2/3\) 分类讨论
为了方便表述,记 \(siz\) 为 \(u\) 的儿子个数,以下简单刻画 \(g \to f\) 的过程
\(f_{u,0}\) 的转移
首先,你什么都不做,直接用 \(g_{siz,0,0}\) 转移肯定没问题。形式化地,有
其次,你可以选择 \((u,fa)\) 这条边,接在某条长度为 \(3\) 的边上也是 OK 的。形式化地,有
记住第二个式子,后面都和这个式子形式差不多
\(f_{u,1}\) 的转移
贯穿 \(u\) 的链长度为 \(1\),则在 \(u\) 内部的长度一定是 \(0\),所以转移来源只有 \(g_{siz,0,0}\)。形式化地,有
并非困难……
\(f_{u,2}\) 的转移
同 \(f_{u,1}\),在 \(u\) 内部的长度一定是 \(1\),因此拼接之后才可能获得长度为 \(2\) 的链。转移是好写的,形式化地,有
可能还算比较好理解?
\(f_{u,3}\) 的转移
同 \(f_{u,1}\),容易发现在 \(u\) 内部的长度一定是 \(2\)。区别于之前的 \(f_{u,0/1}\),长度为 \(2\) 的链影响的是奇偶性,不过这都是细节问题了,转移方程形如
不理解就看转移式子吧,这一部分不是重难点
现在我们会了由 \(g\) 转移到 \(f\),考虑 \(g\) 的内部转移。具体地,思考 \(g_{now,i,o=0/1}\) 的转移来源
第一维度毋庸置疑,一定是 \(now-1\) 贡献给 \(now\)
然后子树合并,依旧是分讨,分讨合并进来的 \(f_{v}\) 的链长度,即分讨 \(f\) 的第二维度
推一推就能搞出来如下式子
码完式子人麻了
答案显然是 \(f_{1,0}\),但问题在于,\(g\) 的转移包 \(O(n^2)\) 的,没前途咋办
随机打乱一下,就有前途了。因为注意到枚举 \(g\) 的第二维是时间复杂度瓶颈,而子树合并在 \(g\) 的第二维度上的表现是 \(+1/-1/0\) 前缀和的形式。在随机打乱之后,这个前缀和的绝对值期望 \(\max\) 是根号量级的,现在就有前途了
代码实现上注意下标偏移,开 long long,以及 \(f,g\) 的初始化
常数优化?时间其实不用优化了,别问,问就是 \(7\)s 时限给的底气。空间上把 \(g\) 的第二维弄到根号量级,同时第一维也可以滚动数组优化
期望时间复杂度 \(O(n \sqrt{n})\),\(g\) 的第二维度算上坐标偏移取 \(2000\) 比较优秀
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define vi vector<int>
#define vp vector<pii>
#define pb push_back
using namespace std;
const int N=2e5+5,M=2e3+5,INF=4e18;
mt19937 RD(time(NULL));
int n,f[N][4],g[2][M][2];vp G[N];
inline void chkmx(int &x,int y){x=max(x,y);return;}
inline void dfs(int u,int fa,int w){
for(auto x:G[u])
if(x.fi!=fa)dfs(x.fi,u,x.se);
memset(g,-0x3f,sizeof(g));
int B=1001,now=1;g[0][B][0]=0;
for(auto x:G[u]){
int v=x.fi;
if(v==fa)continue;
for(int i=1;i<=2*B-1;i++){
for(int o=0;o<=1;o++){
chkmx(g[now][i][o],g[now^1][i][o^1]+f[v][2]);
chkmx(g[now][i][o],g[now^1][i-1][o]+f[v][1]);
chkmx(g[now][i][o],g[now^1][i+1][o]+f[v][3]);
chkmx(g[now][i][o],g[now^1][i][o]+f[v][0]);
}
}
now^=1;
}
chkmx(f[u][0],g[now^1][B][0]);
chkmx(f[u][0],g[now^1][B-1][0]+w);
chkmx(f[u][1],g[now^1][B][0]+w);
chkmx(f[u][2],g[now^1][B+1][0]+w);
chkmx(f[u][3],g[now^1][B][1]+w);
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n-1;i++){
int u,v,w;cin>>u>>v>>w;
G[u].pb(mkp(v,w)),G[v].pb(mkp(u,w));
}
for(int i=1;i<=n;i++)shuffle(G[i].begin(),G[i].end(),RD);
memset(f,-0x3f,sizeof(f));
dfs(1,0,-INF);
cout<<f[1][0]<<'\n';
return 0;
}
K
标算是区间 DP,可是谁写那玩意,随机化草过不香吗?
比较暴力的做法是什么,对于每个卡车二分答案,取 \(\max\) 即可
拍脑袋的结论是,随机打乱之后,前缀 \(\max\) 的数目只有 \(\log\) 个,所以可以通过随机打乱,避免掉很多无效二分
时间复杂度 \(O(n \log m \log v)\)
乱搞做法硬生生地把这个题目变成了普及组难度题目
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=405,M=2.5e5+5;
mt19937 RD(time(NULL));
int n,m,pos[N],mx[N][N];
struct NODE{int s,t,c,r;}a[M];
inline bool check(int id,int mid){
if(mx[a[id].s][a[id].t]*a[id].c>mid)return false;
int rem=mid,tim=0;
for(int i=a[id].s;i<=a[id].t-1;i++){
int d=pos[i+1]-pos[i],cst=d*a[id].c;
if(cst<=rem)rem-=cst;
else tim++,rem=mid-cst;
}
return tim<=a[id].r;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>pos[i];
for(int i=1,s,t,c,r;i<=m;i++)cin>>s>>t>>c>>r,a[i]={s,t,c,r};
for(int i=1;i<=n;i++){
int MX=0;
for(int j=i+1;j<=n;j++){
MX=max(MX,pos[j]-pos[j-1]);
mx[i][j]=MX;
}
}
shuffle(a+1,a+m+1,RD);
int ans=0;
for(int i=1;i<=m;i++){
if(check(i,ans))continue;
int l=max(mx[a[i].s][a[i].t]*a[i].c,ans+1);
int r=(pos[a[i].t]-pos[a[i].s])*a[i].c,res=r;
while(l<=r){
int mid=(l+r)>>1;
if(check(i,mid))r=mid-1,res=mid;
else l=mid+1;
}
ans=max(ans,res);
}
cout<<ans<<'\n';
return 0;
}
L
rz 计算几何,云落不语,只是默默地吃《》
被精度误差各种暴打,代码宣告破产
M
包随机化乱搞好题的!你可以永远相信 CF 的题目质量!
单点修改比较朴素,区间查询就比较抽象了,而且目前已知的数据结构中似乎没有维护这个玩意的东西
其实有,比如带修莫队套根号分治,显然时间复杂度上没有前途
然后你发现这个出现次数都是 \(k\) 的倍数就非常灵性
出现次数这个东西可以用哈希去维护,显然如果一个区间内某种颜色的出现次数是 \(k\) 的倍数,那么该颜色在区间内的和哈希也一定是 \(k\) 的倍数
上面这个是充要转化,问题转化为判定一个颜色的哈希值集合,集合中每一个元素是否均为 \(k\) 的倍数
这玩意肯定暴力维护没有前途,数据结构似乎也做不了。但是我们可以弱化条件,把判定每种颜色的出现次数是 \(k\) 的倍数,转化为出现次数之和
然而,并没有解决核心问题,只用 (r-l+1)%k 去判定还是太草率了,可以用一万个数据卡掉
但是我们可以继续延伸前面的哈希做法,如果每个颜色的哈希值求和之后满足是 \(k\) 的倍数,那么是不是这个区间一定合法?
哈希值的判定方式是一个限制更强的必要不充分条件,但是如果想错判,数据是依赖于你哈希随机的键值的
虽然判错的概率不低,但是我们依旧可以使用多次随机的方式使得判错的概率指数级下降
然后就没有然后了,必要不充分条件在相当大的概率上是充要的,那我们就认定塔式充要的
通过哈希,留给我们的就只有单点修改,区间求和了,简单树状数组维护
本题略微卡常,请非必要不使用 #define int long long,建议使用快读
点击查看代码
#include<bits/stdc++.h>
#define ll long long
#define lwbd lower_bound
using namespace std;
const int N=3e5+5;
const ll MOD1=1e13+37,MOD2=1e13+51;
int n,Q,a[N],t[N],m,b[N<<1];ll rnd[N<<1];bool ans[N];
mt19937_64 RD(time(NULL));
struct que{int l,r,k,o;}q[N];
struct BIT{
ll c[N];
inline ll lb(ll x){return x&(-x);}
inline void clr(){
for(int i=1;i<=n;i++)c[i]=0ll;
return;
}
inline void add(int x,ll v){
for(int i=x;i<=n;i+=lb(i))c[i]+=v;
return;
}
inline ll ask(int x){
ll res=0ll;
for(int i=x;i;i-=lb(i))res+=c[i];
return res;
}
inline ll qry(int l,int r){return ask(r)-ask(l-1);}
}bit;
inline int read(){
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){
if(c=='-')f=-f;
c=getchar();
}
while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
return x*f;
}
signed main(){
n=read(),Q=read();
for(int i=1;i<=n;i++)a[i]=read(),b[++m]=a[i];
for(int i=1;i<=Q;i++){
int opt=read(),l,r,k;
if(opt==1)l=read(),k=read(),q[i]={l,l,k,1};
else if(opt==2)l=read(),r=read(),k=read(),q[i]={l,r,k,2};
b[++m]=k;
}
sort(b+1,b+m+1);
m=unique(b+1,b+m+1)-b-1;
for(int i=1;i<=n;i++)a[i]=lwbd(b+1,b+m+1,a[i])-b;
for(int i=1;i<=Q;i++)
if(q[i].o==1)q[i].k=lwbd(b+1,b+m+1,q[i].k)-b;
for(int i=1;i<=Q;i++)ans[i]=true;
for(int T=1;T<=30;T++){
for(int i=1;i<=m;i++)rnd[i]=(ll)(RD())%MOD1+(ll)(RD())%MOD2;
bit.clr();
memcpy(t,a,sizeof(t));
for(int i=1;i<=n;i++)bit.add(i,rnd[t[i]]);
for(int i=1;i<=Q;i++){
if(q[i].o==1){
int p=q[i].l;
bit.add(p,rnd[q[i].k]-rnd[t[p]]);
t[p]=q[i].k;
}else if(q[i].o==2){
if(!ans[i])continue;
int l=q[i].l,r=q[i].r,k=q[i].k;
if((r-l+1)%k||bit.qry(l,r)%k)ans[i]=false;
}
}
}
for(int i=1;i<=Q;i++)
if(q[i].o==2)puts(ans[i]?"YES":"NO");
return 0;
}
N
BBT 科普性质题
结论:竞赛图中一定存在某个关键点,使得它到任意一点的最短路不超过 \(2\)
证明:考虑数学归纳法
首先一个点是合法的,其次假设前 \(i-1\) 个点构成的竞赛图合法,考虑新插入的结点 \(i\) 所构成的竞赛图是否合法
为了方便表述,记前 \(i\) 个点中的关键点为 \(rt\)
如果 \(rt \to i\) 有边相连,显然合法(I.)
由于是竞赛图,若无 \(rt \to i\),则一定有 \(i \to rt\)。不妨遍历 \(rt\) 的邻接点 \(j\),如果找到与 \(j \to i\) 就显然合法(II.),否则指定 \(i\) 为新的 \(rt\)(III.)
构造显然合法,结论得证
直接说感觉有点晕,结合图来看吧……
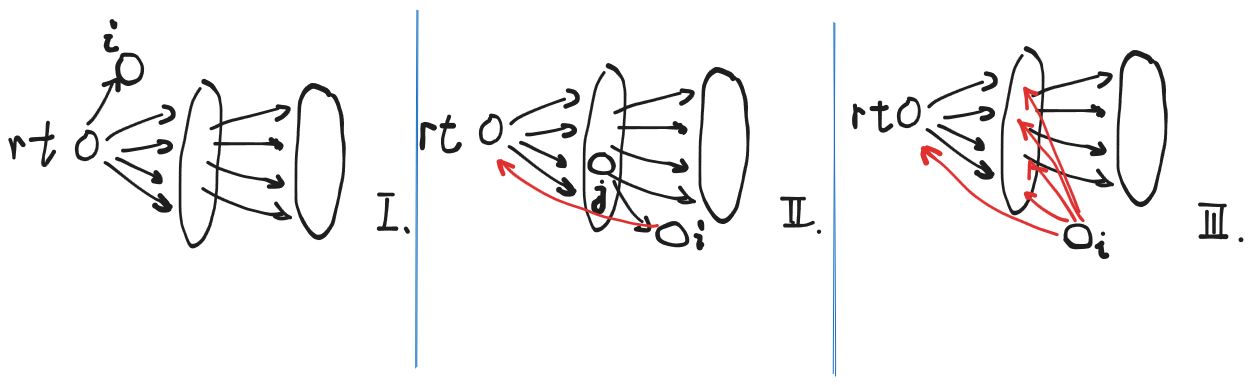
上面的证明非常牛,给出了一种交互的构造方案
问题是时间复杂度没保证呐,一个不小心就 \(O(n^2)\) 了。然后你注意到这是随机化选讲,随机重排一下插入点的顺序,期望时间复杂度就对了
点击查看代码
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=1e6+5;
mt19937 RD(time(NULL));
int fa[N],rt,a[N];
bool sense(int i,int j);
void ins(int x,int n){
if(sense(rt,x)){fa[x]=rt;return;}
vector<int> vec;
for(int i=1;i<n;i++)
if(fa[a[i]]==rt)vec.pb(a[i]);
for(int i:vec)
if(sense(i,x)){fa[x]=i;return;}
fa[rt]=x,rt=x;
for(int i:vec)fa[i]=x;
return;
}
int altar(int n){
for(int i=1;i<=n;i++)fa[i]=0,a[i]=i;
shuffle(a+1,a+n+1,RD);
rt=a[1];
for(int i=2;i<=n;i++)ins(a[i],i);
return rt;
}
O
拍脑袋拍成这个样子也是没谁了
考虑对于每种颜色,用一个矩阵去代替它,然后思考矩阵乘法相关
你发现对于矩阵 \(A\),构造出矩阵 \(A^{-1}\),就能实现一次匹配
因此,进行如下构造。对于第 \(i\) 种颜色,所有下标为奇数的随机一个矩阵 \(A_i\),下标为偶数的随机一个 \({A_i}^{-1}\)
容易发现,当某个区间的矩乘结果为单位矩阵时,这个区间极大概率是合法的
矩阵乘法是有结合律但没有交换律的运算,所以不会被 \(\texttt{123123}\) 这样的数据卡掉
小 Tip:无需写什么高斯消元求矩阵逆,注意到一个叫做对合矩阵的东东性质非常优秀,满足矩阵的逆等于它本身
剩下的就没什么了,简单线段树维护矩阵乘法
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+5,P=1e9+9;
mt19937 RD(time(NULL));
int n,Q;string s;
inline int qpow(int a,int b){
int res=1ll;
while(b){
if(b&1)res=res*a%P;
a=a*a%P,b>>=1;
}
return res;
}
struct Matrix{
int a,b,c,d;
inline void gen(){
int x=(int)(RD())%P,y=(int)(RD())%P;
a=x,b=y,c=(1+(P-a)*a)%P*qpow(b,P-2)%P,d=P-x;
return;
}
friend Matrix operator * (const Matrix &A,const Matrix &B){
Matrix C;
C.a=(A.a*B.a%P+A.b*B.c%P)%P,C.b=(A.a*B.b%P+A.b*B.d%P)%P;
C.c=(A.c*B.a%P+A.d*B.c%P)%P,C.d=(A.c*B.b%P+A.d*B.d%P)%P;
return C;
}
friend bool operator == (const Matrix &A,const Matrix &B){
return A.a==B.a&&A.b==B.b&&A.c==B.c&&A.d==B.d;
}
}M[3],I;
struct Segment_tree{
struct node{int l,r,tag;Matrix A[3];}tr[N<<2];
inline void pushup(int u){
for(int i=0;i<3;i++)tr[u].A[i]=tr[u<<1].A[i]*tr[u<<1|1].A[i];
return;
}
inline void maketag(int u,int v){
if(v==1)swap(tr[u].A[0],tr[u].A[1]),swap(tr[u].A[1],tr[u].A[2]);
if(v==2)swap(tr[u].A[0],tr[u].A[1]),swap(tr[u].A[0],tr[u].A[2]);
tr[u].tag=(tr[u].tag+v)%3;
return;
}
inline void pushdown(int u){
if(!tr[u].tag)return;
int v=tr[u].tag;
maketag(u<<1,v),maketag(u<<1|1,v);
tr[u].tag=0;
return;
}
inline void build(int u,int l,int r){
tr[u].l=l,tr[u].r=r,tr[u].tag=0;
if(l==r){
for(int i=0;i<3;i++)tr[u].A[i]=M[(s[l]-'0'+i)%3];
return;
}
int mid=(l+r)>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
return;
}
inline void modify(int u,int ql,int qr,int v){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r){maketag(u,v);return;}
pushdown(u);
int mid=(l+r)>>1;
if(ql<=mid)modify(u<<1,ql,qr,v);
if(qr>mid)modify(u<<1|1,ql,qr,v);
pushup(u);
return;
}
inline Matrix query(int u,int ql,int qr){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r)return tr[u].A[0];
pushdown(u);
int mid=(l+r)>>1;
if(qr<=mid)return query(u<<1,ql,qr);
if(ql>mid)return query(u<<1|1,ql,qr);
return query(u<<1,ql,qr)*query(u<<1|1,ql,qr);
}
}sgt;
inline void init(){
for(int i=0;i<3;i++)M[i].gen();
I.a=1,I.b=0,I.c=0,I.d=1;
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>Q>>s;s=' '+s;
init();sgt.build(1,1,n);
while(Q--){
int opt,l,r;cin>>opt>>l>>r;
if(opt==1)sgt.modify(1,l,r,1);
else if(opt==2)cout<<(sgt.query(1,l,r)==I?"Yes\n":"No\n");
}
return 0;
}
P
留坑待填
Q
什么鬼东西啊???
先做 \(420\) 次随机,记录每个点作为交互库返回值的次数
然后可以猜测最大值和次大值是根的两个儿子,分别记为 \(x,y\)
最后枚举 \(i\),交互 \((x,y,i)\),如果返回 \(i\),那么 \(i\) 就是根
不会证明,啥都不会,说实话,人麻了
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=(1ll<<18)+5;
mt19937 RD(time(NULL));
int h,n,cnt[N];
inline int ask(int u,int v,int w){
cout<<"? "<<u<<" "<<v<<" "<<w<<'\n';
cout.flush();
int x;cin>>x;
return x;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>h;n=(1<<h)-1;
for(int i=1;i<=420;i++){
int x=RD()%n+1,y=RD()%n+1,z=RD()%n+1;
while(x==y||x==z||y==z)x=RD()%n+1,y=RD()%n+1,z=RD()%n+1;
cnt[ask(x,y,z)]++;
}
int mx=0,cmx=0;
for(int i=1;i<=n;i++){
if(cnt[i]>cnt[mx])cmx=mx,mx=i;
else if(cnt[i]>cnt[cmx])cmx=i;
}
for(int i=1;i<=n;i++)
if(i!=mx&&i!=cmx&&ask(i,mx,cmx)==i){
cout<<"! "<<i<<'\n';cout.flush();
break;
}
return 0;
}
R
留坑待填
后记
世界孤立我任它奚落
完结撒花!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号