9.22 模拟赛

前言

业精于勤荒于嬉，行成于思毁于随

正文（模拟赛）

卦象：大凶

感受：服，一打模拟赛就大凶。先去参加了无聊的升旗仪式，回来调整 5min，开题。然后被 T1 创飞，思考 1.5h 后进度 0%，遂放弃。开 T2，马拉车简单题，被 \(n \le 3000\) 吓唬到了。中途各种线性科技，算上调试代码，码了 3.4k 的代码。剩余 1.5h，开 T3。甚至不会暴力，观测大样例的分布情况后选择总司令做法。最后 1h，目标明确，T4 的暴力分数。通过样例后教练正好进来宣布剩余 20min。这下是真罚坐了，转头回去思考 T1 的正解，以及 T4 半成品的部分分，直到比赛结束。最后 T2 实现细节上复杂度爆炸，挂了 15pts；T4 暴力写挂，挂了 4pts；T3 总司令白嫖 4pts。总分没有破百，道心崩溃

T1

哦，原来看漏了题目条件，自闭 ing。

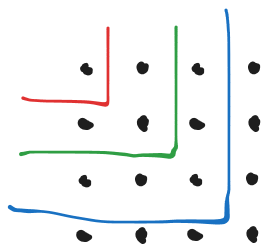
看漏条件的核心就是上图——每个点被点亮的时间是固定的，且一定是分层的

\(n<m\) 的情况可以规约到 \(n=m\) 情况，毕竟最后的 \(m-n\) 轮扩展对方案数的贡献都是 \(\times C\) 的形式，其中 \(C\) 是一个定值，容易用快速幂维护

考虑 \(n=m\) 时候如何去计算答案，注意到题意要求扩展不允许交叉

记 \(f_{i,j}\) 表示关心相邻两行且分别只关心前 \(i\) 个和前 \(j\) 个的方案数

啧，\(|i-j|>1\) 的状态根本没有贡献，所以无需 \(f_{i,j}\)，只需 \(f_{i,0/1/2}\) 即能描述所有情况

转移也是平凡的，分讨 \(0/1/2\) 即可

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e6+5;
int n,m,P,f[N][3];
inline int qpow(int a,int b){
    int res=1;
    while(b){
        if(b&1)res=res*a%P;
        a=a*a%P;b>>=1;
    }
    return res;
}
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n>>m>>P;
    if(n>m)swap(n,m);
    f[1][1]=1;
    for(int i=2;i<=n;i++){
        f[i][0]=(f[i-1][0]+f[i-1][1])%P;
        f[i][1]=(f[i-1][0]+f[i-1][1]+f[i-1][2])%P;
        f[i][2]=(f[i-1][0]+f[i-1][1]+f[i-1][2])%P;
    }
    int ans=1;
    for(int i=2;i<=n-1;i++){
        int x=(f[i][0]+f[i][1]+f[i][2])%P;
        ans=ans*x%P*x%P;
    }
    ans=ans*(qpow((f[n][0]+f[n][1]+f[n][2])%P,m-n))%P;
    cout<<ans<<'\n';
    return 0;
}

T2

算错复杂度而功亏一篑的屑云落

Manacher 求出矩阵中若干横纵线段，对每个点维护包含它的最长横纵线段长度

具体实现上，可以将线段按值域从大到小（类似贴海报）扫描。至于如何维护连续段，血的教训——不能只记录 vis，而应该使用并查集

点击查看代码

#include<bits/stdc++.h>
#define db long double
#define vi vector<int>
#define pb push_back
using namespace std;
const int N=3e3+5;
bool memST;
int n,m;char a[N][N],s[N<<1];int p[N<<1];
struct Line{int l,r,v;}seg1[N][N<<1],seg2[N][N<<1];
int tol1[N],tol2[N];
vi rev[N];bool vis[N];
int r[N][N],c[N][N],ans;
struct dsu{
    int fa[N];
    inline void init(){
        for(int i=1;i<N;i++)fa[i]=i;
        return;
    }
    inline int getfa(int x){return fa[x]==x?x:fa[x]=getfa(fa[x]);}
    inline void merge(int x,int y){
        x=getfa(x),y=getfa(y);
        if(x!=y)fa[y]=x;
        return;
    }
}t;
inline void Manacher1(int id){
    for(int i=0;i<N;i++)p[i]=0;
    int LEN=m*2+1;
	for(int i=1;i<=LEN;i++)s[i]=((i&1)?'#':a[id][i>>1]);
	int c=0,r=0,len=0;
	for(int i=1;i<=LEN;i++){
		len=(r>i?min(p[c*2-i],r-i):1);
		while(i+len<=LEN&&i-len>=1&&s[i+len]==s[i-len])len++;
		if(i+len>r)r=i+len,c=i;
		p[i]=len;
	}
    for(int i=1;i<=LEN;i++)p[i]--;
    for(int i=1;i<=LEN;i++){
        if(!p[i])continue;
        int l=(i-p[i]+1)/2,r=(i+p[i]-1)/2;
        int v=r-l+1;
        seg1[id][++tol1[id]]={l,r,v};
    }
    return;
}
inline void Manacher2(int id){
    for(int i=0;i<N;i++)p[i]=0;
    int LEN=n*2+1;
	for(int i=1;i<=LEN;i++)s[i]=((i&1)?'#':a[i>>1][id]);
	int c=0,r=0,len=0;
	for(int i=1;i<=LEN;i++){
		len=(r>i?min(p[c*2-i],r-i):1);
		while(i+len<=LEN&&i-len>=1&&s[i+len]==s[i-len])len++;
		if(i+len>r)r=i+len,c=i;
		p[i]=len;
    }
    for(int i=1;i<=LEN;i++)p[i]--;
    for(int i=1;i<=LEN;i++){
        if(!p[i])continue;
        int l=(i-p[i]+1)/2,r=(i+p[i]-1)/2;
        int v=r-l+1;
        seg2[id][++tol2[id]]={l,r,v};
    }
    return;
}
inline void work1(int id){
    for(int i=1;i<=N-1;i++)rev[i].clear(),vis[i]=false;
    for(int i=1;i<=tol1[id];i++)rev[seg1[id][i].v].pb(i);
    t.init();
    for(int i=N-1;i>=1;i--){
        if(!rev[i].size())continue;
        for(int o:rev[i]){
            int L=seg1[id][o].l,R=seg1[id][o].r;
            int now=R;
            while(now>=L){
                int nxt=t.getfa(now);
                if(now==nxt)r[id][now]=i,t.merge(t.getfa(now-1),now);
                now=t.getfa(now);
            }
        }
    }
    return;
}
inline void work2(int id){
    for(int i=1;i<=N-1;i++)rev[i].clear(),vis[i]=false;
    for(int i=1;i<=tol2[id];i++)rev[seg2[id][i].v].pb(i);
    t.init();
    for(int i=N-1;i>=1;i--){
        if(!rev[i].size())continue;
        for(int o:rev[i]){
            int L=seg2[id][o].l,R=seg2[id][o].r;
            int now=R;
            while(now>=L){
                int nxt=t.getfa(now);
                if(now==nxt)c[now][id]=i,t.merge(t.getfa(now-1),now);
                now=t.getfa(now);
            }
        }
    }
    return;
}
bool memED;
int main(){
    // freopen("mat.in","r",stdin);
    // freopen("mat.out","w",stdout);
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>(a[i]+1);
    for(int i=1;i<=n;i++)Manacher1(i);
    for(int j=1;j<=m;j++)Manacher2(j);
    for(int i=1;i<=n;i++)work1(i);
    for(int j=1;j<=m;j++)work2(j);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            ans=max(ans,r[i][j]*c[i][j]);
    cout<<ans<<'\n';
    return 0;
}

T3

留坑待填

T4

破大防

\(t_0>t_1\)，直接飞翔，跨过山和大海……

现在考虑游泳的情况，钦定飞翔非常劣（比如特殊性质二），感性理解人与龙的行进过程。人龙游泳，龙游不动了，人就向前获取能量，直到收集足够，返回寻龙继续游泳

注意到游泳你无法避免，最小化答案等价于最小化走路时长

考虑贪心，为了方便表述，记 \(a_i\) 的前缀和为 \(s_i\)。人如果无需经过道路 \(i \to i+1\)，则必然有 \(s_{i-1}- (i-1)d \ge 0\)

这个时候再把飞翔加进来，由于飞翔是对贡献清零，所以容易想根据飞翔分段。换句话说，两次飞翔操作之间就是上面只有游泳与走路的情况

容易想到 \(O(n^2)\) 的 DP，记 \(f_i\) 表示飞翔到 \(i\) 的最小时间。转移是经典的连续段 DP，枚举上一次飞翔结束的位置 \(j\)，方程大概是 \(f_i = \min \{ f_j + w(j,i-1) \}\) 的形式

在转移 \(i\) 的过程中，涉及到 \(a_i\) 是否被提前获取，可能需要 \(f_{i,0/1}\) 的状态设计

（转移是简单的，代码是困难的）

简单说一下优化，注意到前面那个 \(s_{i-1} - (i-1)d \ge 0\) 的情况再连续段 DP 的转移中也是适用的。其本质都是，区间获取的能量之和要多于游泳经过这段区间所消耗的体力

区间贡献可以拆成前缀差分，对于每个 \(i\)，维护 \(g_i,h_i\)，分别表示 \(s_{i-1}-(i-1)d\) 和 \(s_{i}-(i-1)d\)

根据前面的限制条件，可以写出一个关于 \(g,h\) 的不等关系。丢到权值线段树上，可以简单维护

现在飞翔的用 DP 连续段结算去维护，游泳也在区间的前缀差分保证了，只差走路了

回到 \(O(n^2)\) 的 DP 中来，推式子，观测结论

\[\begin{aligned} s_{i-1} - s_{j-1} &\ge (i-j-1)d \newline s_{i-1} - i \cdot d &\ge s_{j-1} - (j-1) \cdot d \end{aligned} \]

注意到起点 \(j\) 固定的时候，\(i \to i+1\) 是否行走已经确定了，与终点的位置没有特别大的关系

而终点 \(i\) 确定的时候，符合要求的 \(j\) 一定符合上述式子，在值域上形如一个前缀。而这个值域非常神奇，它正好是我们权值线段树上的下标！

所以你可以直接在权值线段树上修改一个前缀，把贡献都丢上去即可

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define ubbd upper_bound
using namespace std;
const int N=5e5+5,INF=4e18;
int n,d,t0,t1,t2,a[N],pre[N],b[N<<1],tot;
struct Segment_tree{
    struct node{int l,r,mn,tag;}tr[N<<3];
    inline void pushup(int u){
        tr[u].mn=min(tr[u<<1].mn,tr[u<<1|1].mn);
        return;
    }
    inline void mketag(int u,int v){
        tr[u].mn+=v,tr[u].tag+=v;
        return;
    }
    inline void pushdown(int u){
        if(!tr[u].tag)return;
        int v=tr[u].tag;
        mketag(u<<1,v),mketag(u<<1|1,v);
        tr[u].tag=0;
        return;
    }
    inline void build(int u,int l,int r){
        tr[u].l=l,tr[u].r=r,tr[u].tag=0;
        if(l==r){tr[u].mn=INF;return;}
        int mid=(l+r)>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        pushup(u);
        return;
    }
    inline void modify(int u,int pos,int v){
        int l=tr[u].l,r=tr[u].r;
        if(l==r){tr[u].mn=min(tr[u].mn,v);return;}
        pushdown(u);
        int mid=(l+r)>>1;
        if(pos<=mid)modify(u<<1,pos,v);
        else modify(u<<1|1,pos,v);
        pushup(u);
        return;
    }
    inline void update(int u,int ql,int qr,int v){
        if(ql>qr)return;
        int l=tr[u].l,r=tr[u].r;
        if(ql<=l&&qr>=r){mketag(u,v);return;}
        pushdown(u);
        int mid=(l+r)>>1;
        if(ql<=mid)update(u<<1,ql,qr,v);
        if(qr>mid)update(u<<1|1,ql,qr,v);
        pushup(u);
        return;
    }
    inline int query(int u,int ql,int qr){
        if(ql>qr)return INF;
        int l=tr[u].l,r=tr[u].r;
        if(ql<=l&&qr>=r)return tr[u].mn;
        pushdown(u);
        int mid=(l+r)>>1,res=INF;
        if(ql<=mid)res=min(res,query(u<<1,ql,qr));
        if(qr>mid)res=min(res,query(u<<1|1,ql,qr));
        return res;
    }
}sgt;
inline int fnd(int x){return upbd(b+1,b+tot+1,x)-b-1;}
inline void solve(){
    cin>>n>>d>>t0>>t1>>t2;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=1;i<=n;i++)pre[i]=pre[i-1]+a[i];
    for(int i=1;i<=n;i++)b[++tot]=pre[i]-d*i,b[++tot]=pre[i-1]-d*i;
    sort(b+1,b+tot+1);tot=unique(b+1,b+tot+1)-b-1;
    sgt.build(1,1,tot);sgt.modify(1,fnd(-d),0);
    int ans=INF;
    for(int i=2;i<=n;i++){
        int o1=sgt.query(1,1,fnd(pre[i]-d*(i-1)-1))+t1-t0;
        int o2=sgt.query(1,1,fnd(pre[i-1]-d*(i-1)-1))+t1-t0;
        sgt.modify(1,fnd(pre[i]-d*i),o1);
        sgt.modify(1,fnd(pre[i-1]-d*i),o2);
        sgt.update(1,1,fnd(pre[i-1]-d*i),-(t2*2));
        if(i==n)ans=o2;
    }
    ans=min(ans,sgt.query(1,1,fnd(pre[n]-d*n)));
    cout<<ans+(t2*2+t0)*(n-1)<<'\n';
    return;
}
inline void clr(){
    for(int i=1;i<=n;i++)pre[i]=0;
    for(int i=1;i<=tot;i++)b[i]=0;
    tot=0;
    return;
}
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int C,T;cin>>C>>T;while(T--)solve(),clr();
    return 0;
}

小结

心态 -3

后记

世界孤立我任它奚落

完结撒花！