9.16 jsy 支配对选讲

前言

业精于勤荒于嬉，行成于思毁于随

正文（加餐）

支配对选讲，象征性意义的放一个题单（题单是个人私有的，毕竟是别人辛辛苦苦积累的东西，公开容易带来知识产权上的一些纠纷）

支配对这一概念，目前云落对于支配对的理解就是，另一种形式的“偏序”

可能第一次接触支配对的概念应该是在单调队列 or 单调栈当中，再者就是一些 DP 优化当中。核心思想就是观测一个由点对构成的集合 $S$，对于某个 $S' \subset S$，发现 $S'$ 内的所有点对总是优于 $S-S'$。那么，我们就不需要枚举 $S$ 中的所有元素，而是只需要枚举 $S'$ 中的所有元素即可

对于任意的 $x \in S ,\ y \in S-S'$，我们称点对 $x$ 支配了点对 $y$，其中点对 $x$ 可被称为支配对

A

题面：给定序列 $a,b$，每次给定区间 $[l,r]$，要从区间内选出 $i,j$ 满足 $a_i=a_j$，求 $b_i+b_j$ 的最大值

直接 $O(n^2)$ 固然是可行的，但也肯定是过不了的，考虑支配关系，试图挖掘性质 ing

假设贡献答案的部分点对 $(i,j)$ 满足 $i<j \ \land \ a_i<a_j$（假设显然是不影响答案正确性的，因为 $i<j \land a_i>a_j$ 的情况可以把序列倒过来再做一遍），容易发现当 $i$ 固定的时候，$j$ 的答案一定是 $i$ 以后的前缀 $\max$ 的位置

不妨设这些位置依次为 $j_0,j_1,\dots,j_k$

注意到只有点对 $(i,j_0)$ 可能造成贡献，因为对于任意的 $p(p \neq 0)$，总有点对 $(i,j_p)$ 被点对 $(i,j_{p-1})$ 支配

因此，对于固定点 $i$ 来说，你只需要维护 $j_0$ 即可，也就是 $O(1)$ 个点

那么总的支配对数量就是 $O(n)$，直接枚举比较即可

B

讲个乐子，三倍经验

经验一 and 经验二 and 经验三

虽然这题紫的发黑，但是了解支配对之后，再加上一点脑电波，就可以轻松切掉

依旧假设 $i<j \land a_i <a_j$……嗯，这假设对吗？包对的，另一种情况你让 $a_i \gets INF - a_i$ 再做一遍就好了嘛

那么，固定 $i$ 之后，只有 $i$ 之后且比 $a_i$ 大的前缀 $\min$ 的位置 $j$ 才有可能贡献答案

不妨设这些位置分别为 $j_0,j_1,\dots,j_k$

看上去还是 $O(n^2)$ 的，比如构造一个单调递减的序列就凉凉了，要进一步提取性质

先从这些前缀 $\min$ 位置中抽取两个幸运儿，分别记作 $x,y$，并且钦定 $(i,x)$ 已经是一个支配对。显然我们需要考察 $(i,y)$ 不被支配的性质

容易列出式子 $a_i<a_y<a_x$，而且进一步地，$y$ 应当还需满足

\[a_y-a_i < a_x -a_y \]

为啥子嘞？因为不满足这个条件的话就被 $(x,y)$ 给支配了。

简单整理一下，有

\[a_y < \frac{a_i+a_x}{2} \]

你发现每新加入一个支配对 $(i,y)$，不等号右边的规模都会减半，所以是 $\log$ 的

那么总的支配对数目就是 $O(\log)$ 的，非常可做

维护 $j_0$ 的位置可以扫描线 $+$ 动态开点权值线段树，每次加入新的支配对 $(i,y)$ 就可以在找到 $j_0$ 之后树状数组去做

贴个代码辅助理解

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define vi vector<int>
#define vp vector<pii>
#define pb push_back
using namespace std;
const int N=3e5+5,INF=1e9;
int n,m,a[N],ans[N];
vp vec[N];
struct Segment_tree{
	int rt,cnt;
	struct node{int l,r,mx;}tr[N<<5];
	inline void pushup(int u){
		tr[u].mx=max(tr[tr[u].l].mx,tr[tr[u].r].mx);
		return;
	}
	inline void clr(){
		for(int i=1;i<=cnt;i++)tr[i]={0,0,0};
		rt=cnt=0;
		return;
	}
	inline void modify(int &u,int l,int r,int pos,int v){
		if(!u)u=++cnt;
		if(l==r){tr[u].mx=max(tr[u].mx,v);return;}
		int mid=(l+r)>>1;
		if(pos<=mid)modify(tr[u].l,l,mid,pos,v);
		else modify(tr[u].r,mid+1,r,pos,v);
		pushup(u);
		return;
	}
	inline int query(int u,int l,int r,int ql,int qr){
		if(!u)return 0;
		if(ql<=l&&qr>=r)return tr[u].mx;
		int mid=(l+r)>>1,res=0;
		if(ql<=mid)res=max(res,query(tr[u].l,l,mid,ql,qr));
		if(qr>mid)res=max(res,query(tr[u].r,mid+1,r,ql,qr));
		return res;
	}
}sgt;
struct BIT{
	int c[N];
	inline int lb(int x){return x&(-x);}
	inline void clr(){
		for(int i=1;i<=n;i++)c[i]=INF;
		return;
	}
	inline void add(int x,int v){
		for(int i=x;i;i-=lb(i))c[i]=min(c[i],v);
		return;
	}
	inline int ask(int x){
		int res=INF;
		for(int i=x;i<=n;i+=lb(i))res=min(res,c[i]);
		return res;
	}
}bit;
inline void solve(){
	bit.clr();sgt.clr();
	for(int i=1;i<=n;i++){
		int pos=sgt.query(sgt.rt,0,INF,a[i],INF);
		while(pos){			
			bit.add(pos,a[pos]-a[i]);
			pos=sgt.query(sgt.rt,0,INF,a[i],(a[i]+a[pos]-1)/2);
		}
		sgt.modify(sgt.rt,0,INF,a[i],i);
		for(auto x:vec[i])ans[x.se]=min(ans[x.se],bit.ask(x.fi));
	}
	return;
}
signed main(){
	// freopen("in.txt","r",stdin);
	// freopen("out.txt","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	cin>>m;
	for(int i=1,l,r;i<=m;i++)cin>>l>>r,vec[r].pb(mkp(l,i));
	for(int i=1;i<=m;i++)ans[i]=INF;
	solve();
	for(int i=1;i<=n;i++)a[i]=INF-a[i];
	solve();
	for(int i=1;i<=m;i++)cout<<ans[i]<<'\n';
	return 0;
}

C

题目传送门

有数据结构的地方，就一定有 Ynoi

首先维护路径信息，你完全可以使用淀粉质技巧。根据一些经验，当分治中心确定的时候，同属于一棵子树内的点对 $(i,j)$ 一定不会在当前这一层贡献答案

不是？那不就转化为 A 了吗？每分治出来一层就单调栈维护支配对，根据淀粉质的时间复杂度证明，这么做一点问题没有。然后把查询离线扫描线，相当于给支配对二维数点

额，算法与数据结构捏合的 Ynoi，又是爱上淀粉质的一天

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define vi vector<int>
#define vp vector<pii>
#define pb push_back
using namespace std;
const int N=5e5+5,INF=4e18;
int n,Q,head[N],tot,ans[N];
struct Edge{int to,nxt,val;}e[N<<1];
int siz[N];bool vis[N];
pii a[N],stk[N];int tol,tp;
vp p[N],q[N];
struct BIT{
	int c[N];
	inline int lb(int x){return x&(-x);}
	inline void init(){
		for(int i=1;i<N;i++)c[i]=INF;
		return;
	}
	inline void add(int x,int v){
		for(int i=x;i<N;i+=lb(i))c[i]=min(c[i],v);
		return;
	}
	inline int ask(int x){
		int res=INF;
		for(int i=x;i;i-=lb(i))res=min(res,c[i]);
		return res;
	}
}bit;
inline void add(int u,int v,int w){
	e[++tot]={v,head[u],w};head[u]=tot;
	return;
}
inline void getsz(int u,int fa){
	siz[u]=1;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa||vis[v])continue;
		getsz(v,u);siz[u]+=siz[v];
	}
	return;
}
inline void getzx(int u,int fa,int rt,int &mn,int &g){
	int sub=siz[rt]-siz[u];
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa||vis[v])continue;
		sub=max(sub,siz[v]);
		getzx(v,u,rt,mn,g);
	}
	if(sub<mn)mn=sub,g=u;
	return;
}
inline void dfs(int u,int fa,int dis){
	a[++tol]=mkp(u,dis);
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to,w=e[i].val;
		if(v==fa||vis[v])continue;
		dfs(v,u,dis+w);
	}
	return;
}
inline void solve(int u){
	getsz(u,0);
	int mn=n,g=0;
	getzx(u,0,u,mn,g);vis[g]=true;
	tol=0;dfs(g,0,0);sort(a+1,a+tol+1);
	tp=0;
	for(int i=1;i<=tol;i++){
		while(tp&&stk[tp].se>=a[i].se){
			p[stk[tp].fi].pb(mkp(a[i].fi,a[i].se+stk[tp].se));
			tp--;
		}
		if(tp)p[stk[tp].fi].pb(mkp(a[i].fi,a[i].se+stk[tp].se));
		stk[++tp]=a[i];
	}
	for(int i=head[g];i;i=e[i].nxt){
		int v=e[i].to;
		if(vis[v])continue;
		solve(v);
	}
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n-1;i++){
		int u,v,w;cin>>u>>v>>w;
		add(u,v,w),add(v,u,w);
	}
	cin>>Q;
	for(int i=1;i<=Q;i++){
		int l,r;cin>>l>>r;
		q[l].pb(mkp(r,i));
	}
	solve(1);
	bit.init();
	for(int i=n;i>=1;i--){
		for(auto x:p[i])bit.add(x.fi,x.se);
		for(auto x:q[i])ans[x.se]=bit.ask(x.fi);
	}
	for(int i=1;i<=Q;i++)cout<<(ans[i]>=INF?-1:ans[i])<<'\n';
	return 0;
}

D

对 $y$ 分治，再结合 $x_i,x_j$ 分居 $y$ 轴两侧，容易发现 $(x_i,y_i)$ 与 $(x_j,y_j)$ 被分割在两个不同的 $\frac{1}{4}$ 平面上

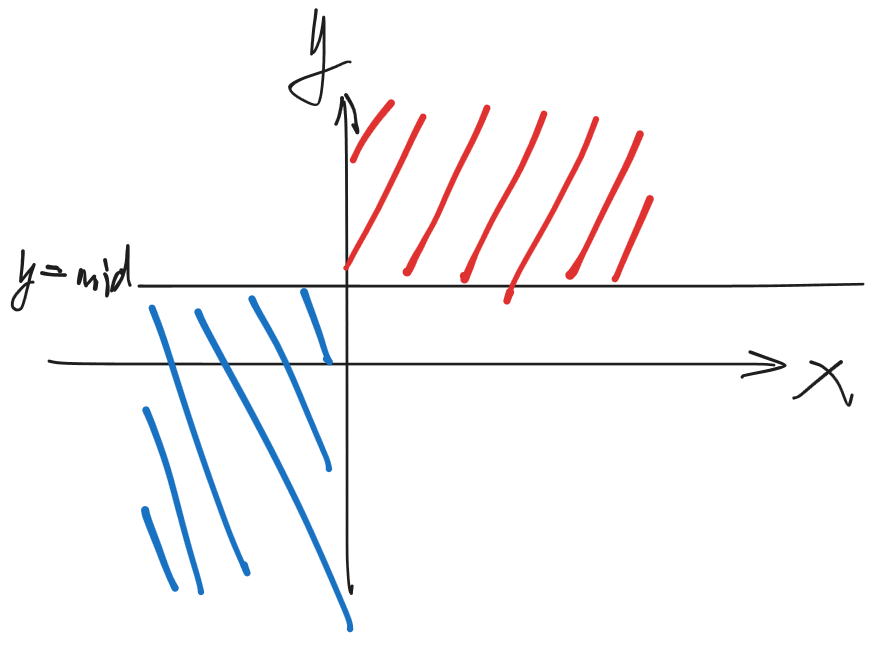
接下来考虑查询 $[l,r]$，令 $[l,r]$ 的答案为由点 $i$ 和点 $j$ 贡献

记分居两个四分之一平面内 $w$ 最大的分别为 $p,q$，对于任意一个点对 $x,y$，你总是可以把 $x$ 调整为 $p$，或者把 $y$ 调整为 $q$，使得答案不劣

显然发现了支配关系，一层分治 $O(n)$ 个支配对，总计 $O(n \log n)$ 个支配对

分治把支配对扫出来之后简单扫描线计算答案即可

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define vi vector<int>
#define vp vector<pii>
#define pb push_back
#define lwbd lower_bound
using namespace std;
const int N=1e5+5,M=5e5+5;
int n,Q,b[N<<1],ans[M],tree[N];
vp p[N],q[N];
struct node{int x,y,w;}a[N<<1];
struct BIT{
	int c[N];
	inline int lb(int x){return x&(-x);}
	inline void clr(){
		for(int i=1;i<=n;i++)c[i]=-1;
		return;
	}
	inline void add(int x,int v){
		for(int i=x;i<=n;i+=lb(i))c[i]=max(c[i],v);
		return;
	}
	inline int ask(int x){
		int res=-1;
		for(int i=x;i;i-=lb(i))res=max(res,c[i]);
		return res;
	}
}bit;
inline bool cmp(node s,node t){return s.y<t.y;}
inline void solve(int l,int r){
	if(l==r)return;
	int mid=(l+r)/2;
	solve(l,mid),solve(mid+1,r);
	int o=0;
	for(int i=l;i<=mid;i++)
		if(a[i].x<=n&&a[i].w>a[o].w)o=i;
	if(o){
		for(int i=mid+1;i<=r;i++)
			if(a[i].x>n)p[a[o].x].pb(mkp(a[i].x-n,a[o].w+a[i].w));
	}
	o=0;
	for(int i=mid+1;i<=r;i++)
		if(a[i].x>n&&a[i].w>a[o].w)o=i;
	if(o){
		for(int i=l;i<=mid;i++)
			if(a[i].x<=n)p[a[i].x].pb(mkp(a[o].x-n,a[o].w+a[i].w));
	}
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=2*n;i++)cin>>a[i].x>>a[i].y>>a[i].w,b[i]=a[i].x;
	sort(a+1,a+2*n+1,cmp),sort(b+1,b+2*n+1);
	for(int i=1;i<=2*n;i++)a[i].x=lower_bound(b+1,b+2*n+1,a[i].x)-b;
	solve(1,2*n);
	cin>>Q;
	for(int i=1;i<=Q;i++){
		int l,r;cin>>l>>r;
		l=lwbd(b+1,b+2*n+1,l)-b-1,r=lwbd(b+1,b+2*n+1,r)-b-1-n;
		q[l].pb(mkp(r,i));
	}
	for(int i=1;i<=Q;i++)ans[i]=-1;
	bit.clr();
	for(int i=1;i<=n;i++){
		for(auto x:p[i])bit.add(n-x.fi+1,x.se);
		for(auto x:q[i])ans[x.se]=max(ans[x.se],bit.ask(n-x.fi));
	}
	bit.clr();
	for(int i=n;i>=1;i--){
		for(auto x:q[i])ans[x.se]=max(ans[x.se],bit.ask(x.fi));
		for(auto x:p[i])bit.add(x.fi,x.se);
	}
	for(auto x:q[0])ans[x.se]=max(ans[x.se],bit.ask(x.fi));
	for(int i=1;i<=Q;i++)cout<<ans[i]<<'\n';
	return 0;
}

E

题面：给定排列 $p$，每次查询区间 $[l,r]$，求 $[l,r]$ 内满足 $l \le i < j \le r$ 的 $\varphi(p_i \times p_j)$ 的最大值

需要知道一个（套路的）性质……

\[\varphi(p_ip_j)=\frac{\varphi(p_i)\varphi(p_j)\gcd(p_i,p_j)}{\varphi(\gcd(p_i,p_j))} \]

性质的证明放在最后，先假设这个是对的

典中典之枚举 $\gcd$，在序列中提取出 $\gcd$ 的倍数的所有位置，然后显然是想最大化 $\varphi(p_i)\varphi(p_j)$ 的值

基本上又和 A 题一样了，依旧是对于 $i$ 来说，在右侧找第一个比 $\varphi(p_i)$ 大的 $\varphi(p_j)$

容易证明这个支配关系是正确的

接下来倒回去推式子，证明如下：

\[\begin{aligned} \varphi(xy) &= xy \prod _{i \in S \cup T}(1-\frac{1}{p_i}) \\ &= \frac{ x \prod \limits_{i \in S} (1-\frac{1}{p_i}) \cdot y \prod \limits_{j \in T}(1- \frac{1}{p_j})}{\prod \limits_{k \in S \cap T} (1-\frac{1}{p_k})} \\ &= \varphi(x) \varphi(y) \cdot \frac{\gcd(x,y)}{\varphi(\gcd(x,y))} \end{aligned} \]

数论可真是太有意思了……

F

题目传送门

~~小清新~~

首先根据数论题的经验，看到 $\gcd$ 想到枚举 $\gcd$ 的约数 $d$，把这个过程稍微形式化一下，可以这么说：

定义一个区间 $[l,r]$ 是 “$d$ 亲和”的，当且仅当存在 $l<m<r$ 满足 $d \mid \gcd(a_l,a_m,a_r)$。特别地，对于区间 $[l,r]$，若不存在 $[l',r'] \subset [l,r]$，则我们称 $[l,r]$ 是“极短 $d$ 亲和”的

注意到对于一个序列来说，“极短 $d$ 亲和”的区间只有 $O(n \cdot d(V))$ 个

并且这些区间性质优秀，显然如果可以求出这些“极短 $d$ 亲和”的区间，我们只需要套一层二维数点就能计算答案

考虑怎么求出所有的“极短 $d$ 亲和”的区间

先对每个因数 $d$ 存储它的倍数在数列中的位置并排序。枚举 $l$，首先 $m-l$ 自然越小越好，所以直接取相邻的两个位置作为 $l$ 和 $m$ 即可，问题转化为找 $r$

lower_bound 就有点太抽象了，约数个数是根号的，二分是 $\log$ 的，根号 $\log$ 凑一块就容易在时限上出事

但是又没说一定要在线，你发现抛开 $d$ 整除的条件，限制 $r$ 的条件只有一个，即

\[m-l \le r-m \]

稍微整理一下，就有

\[r \ge 2m-l \]

把这些可能的 $r$ 挂在 $2m-l$ 上，倒着扫一遍就好了嘛

我们现在已经获得了 $O(n \cdot d(V))$ 个支配对，该计算答案了

然而好像不太好弄，$O(\log n)-O(\log n)$ 的树状数组二维数点有点劣，毕竟你发现扫描线过程中有 $O(n \cdot d(V))$ 组修改和 $O(Q)$ 组查询

都说到这肯定复杂度平衡呐！用分块维护二维数点，做到单次 $O(1)-O(\sqrt{n})$，所以总复杂度就是严格的根号量级

当然据说根号 $\log$ 卡卡常数也能过

点击查看代码

#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define vi vector<int>
#define vp vector<pii>
#define pb push_back
using namespace std;
const int N=1.5e5+5,B=400,V=1e6+5;
int n,Q,a[N],lst[V];vi d[V];
int L[B],R[B],blk[N],val[N],tag[N],siz,tot;
vp vec[N<<1],p[N],q[N];int ans[N];
inline void init(int n){
	for(int i=1;i<=n;i++)
		for(int j=i;j<=n;j+=i)d[j].pb(i);
	return;
}
inline void build(){
	siz=sqrt(n),tot=n/siz;
	for(int i=1;i<=tot;i++)L[i]=(i-1)*siz+1,R[i]=i*siz;
	if(R[tot]<n){
		tot++;
		L[tot]=R[tot-1]+1,R[tot]=n;
	}
	for(int i=1;i<=tot;i++)for(int j=L[i];j<=R[i];j++)blk[j]=i;
	return;
}
inline void upd(int u,int v){
	val[u]=max(val[u],v);
	tag[blk[u]]=max(tag[blk[u]],v);
	return;
}
inline int get(int l,int r){
	int res=0;
	if(blk[l]==blk[r]){
		for(int i=l;i<=r;i++)res=max(res,val[i]);
		return res;
	}
	for(int i=l;i<=R[blk[l]];i++)res=max(res,val[i]);
	for(int i=L[blk[r]];i<=r;i++)res=max(res,val[i]);
	for(int i=blk[l]+1;i<=blk[r]-1;i++)res=max(res,tag[i]);
	return res;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>Q;init(V-5);
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++){
		for(int x:d[a[i]]){
			if(!lst[x])continue;
			vec[2*i-lst[x]].pb(mkp(lst[x],x));
		}
		for(int x:d[a[i]])lst[x]=i;
	}
	for(int i=1;i<=V-5;i++)lst[i]=0;
	for(int i=n;i>=1;i--){
		for(int x:d[a[i]])lst[x]=i;
		for(auto x:vec[i]){
			if(!lst[x.se])continue;
			p[lst[x.se]].pb(mkp(x.fi,x.se));
		}
	}
	build();
	for(int i=1,l,r;i<=Q;i++)cin>>l>>r,q[r].pb(mkp(l,i));
	for(int i=1;i<=n;i++){
		for(auto x:p[i])upd(x.fi,x.se);
		for(auto x:q[i])ans[x.se]=get(x.fi,i);
	}
	for(int i=1;i<=Q;i++)cout<<ans[i]<<'\n';
	return 0;
}

G

被 dsu on tree 逼疯的一天

考虑什么样的点对可以对答案造成贡献。发现若一个区间 $[l,r]$ 内，存在一组 $(x,y)$，使得 $lca(x,y)=u$ 且同时存在 $x<a<b<y$，满足 $lca(a,b)=u$，则 $(x,y)$ 属于无效贡献。换言之，在上述情况下，$(x,y)$ 被 $(a,b)$ 支配

由题意，套路地去想枚举 $lca$，显然如果 $lca(x,y)=u$，那么 $x,y$ 一定分别属于 $u$ 的两棵不同子树（当然，除了 $lca(u,u)=u$ 这一特殊情况；至于 $lca(u,x)=u$ 的情况，它一定被 $lca(u,u)=u$ 这一情况支配，不作考虑）

概括本题支配对的性质：要么是本身与本身，形如 $(u,u)$；要么是对于某个 $lca$ 来说，在树上编号极近的一对点

那么根据支配对的思想，当枚举 $u$ 并固定 $u$ 某棵子树内的 $x$ 时，我们要去找其它子树中编号离 $x$ 最近的 $y$。而这一过程直接做是 $O(n^2)$ 的，需要用一个 dsu on tree 来做到 $O(n \log n)$

支配对总数是 $O(n \log n)$ 的，为啥子嘞？因为根据 dsu on tree 的相关结论，你发现一个点只会被遍历到 $\log n$ 次，而遍历到一次就只会产生 $O(1)$ 个支配对，所以支配对总数就是 $O(n \log n)$ 的

代码实现上，你考虑对于一个 $x$，找支配对的过程相当于 $x$ 在其它子树构成的点集中寻找编号上的前驱与后继，用一个 set 维护即可（注意一些特判一些边界情况）

最后计算答案是对 $dep_{lca}$ 计数，显然你把所有支配对求出来，然后跑一遍静态区间数颜色就对了

云落实现的时候不知道为什么 Ctrl+C 的 HH 的项链假了，也不知道为什么正着循环初值为 $-1$ 就不对，反而倒着循环初值为 $n+1$ 就对了，神秘代码

时间复杂度两支 $\log$

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define vi vector<int>
#define vp vector<pii>
#define pb push_back
#define lwbd lower_bound
#define upbd upper_bound
using namespace std;
const int N=1e5+5,M=5e5+5;
int n,m,head[N],tot;
struct Edge{int to,nxt,val;}e[N<<1];
int siz[N],son[N],dis[N],col[N];
set<int> S;vp p[N],q[N];
int lst[N],ans[M];
struct BIT{
	int c[N];
	inline int lb(int x){return x&(-x);}
	inline void add(int x,int v){
		for(int i=x;i<=n;i+=lb(i))c[i]+=v;
		return;
	}
	inline int ask(int x){
		int res=0;
		for(int i=x;i;i-=lb(i))res+=c[i];
		return res;
	}
}bit;
inline void add(int u,int v,int w){
	e[++tot]={v,head[u],w};head[u]=tot;
	return;
}
inline void init(int u,int fa){
	siz[u]=1;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to,w=e[i].val;
		if(v==fa)continue;
		dis[v]=dis[u]+w;init(v,u);siz[u]+=siz[v];
		if(siz[son[u]]<siz[v])son[u]=v;
	}
	return;
}
inline void upd(int u,int c){
	auto it1=S.lwbd(u),it2=S.upbd(u);
	int pr=(it1==S.begin()?0:(*(--it1)));
	int nx=(it2==S.end()?0:(*it2));
	if(pr)p[pr].pb(mkp(u,c));
	if(nx)p[u].pb(mkp(nx,c));
	return;
}
inline void work(int u,int fa,int col){
	upd(u,col);
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa)continue;
		work(v,u,col);
	}
	return;
}
inline void ins(int u,int fa){
	S.insert(u);
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa)continue;
		ins(v,u);
	}
	return;
}
inline void dfs(int u,int fa,int o){
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa||v==son[u])continue;
		dfs(v,u,1);
	}
	if(son[u])dfs(son[u],u,0);
	upd(u,col[u]);S.insert(u);
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa||v==son[u])continue;
		work(v,u,col[u]);ins(v,u);
	}
	if(o)S.clear();
	return;
}
signed main(){

	// freopen("in.txt","r",stdin);
	// freopen("out.txt","w",stdout);

	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n-1;i++){
		int u,v,w;cin>>u>>v>>w;
		add(u,v,w),add(v,u,w);
	}
	init(1,0);
	for(int i=1;i<=n;i++)col[i]=dis[i];
	sort(dis+1,dis+n+1);
	int T=unique(dis+1,dis+n+1)-dis-1;
	for(int i=1;i<=n;i++)col[i]=lwbd(dis+1,dis+T+1,col[i])-dis;
	dfs(1,0,0);
	for(int i=1;i<=n;i++)p[i].pb(mkp(i,col[i]));

	// for(int i=1;i<=n;i++){
	// 	for(auto x:p[i])cerr<<"("<<i<<","<<x.fi<<","<<x.se<<")"<<' ';
	// 	cerr<<endl;
	// }
	
	for(int i=1;i<=T;i++)lst[i]=n+1;
	for(int i=1,l,r;i<=m;i++)cin>>l>>r,q[l].pb(mkp(r,i));
	for(int i=n;i>=1;i--){
		for(auto x:p[i]){
			bit.add(lst[x.se],-1);
			lst[x.se]=min(lst[x.se],x.fi);
			bit.add(lst[x.se],1);
		}
		for(auto x:q[i])ans[x.se]=bit.ask(x.fi);
	}
	for(int i=1;i<=m;i++)cout<<ans[i]<<'\n';
	return 0;
}

/*
(1,2,5) (1,1,5) 
(2,10,7) (2,5,7) (2,3,3) (2,2,8) 
(3,7,2) (3,5,3) (3,4,5) (3,3,1) 
(4,5,5) (4,4,6) 
(5,10,7) (5,6,7) (5,5,6) 
(6,10,7) (6,8,4) (6,7,3) (6,6,8) 
(7,8,3) (7,7,2) 
(8,10,4) (8,9,3) (8,8,4) 
(9,10,3) (9,9,3) 
(10,10,7)
*/

H

题目传送门

评黑全是因为后面需要使用大量的 jiao

还是套路的先抓出一组 $a_x,a_y$（依旧钦定 $a_x<a_y$），令 $u=lca(x,y)$，然后去考察 $a_u$ 与 $a_x,a_y$ 之间的大小关系

为了方便分析与表述，不妨设 $a_x<a_y$，显然本质不同的大小关系只有如下三种

$a_u < a_x < a_y$
$a_x < a_u < a_y$
$a_x < a_y < a_u$

这里不需要考虑取等条件，如果出现取等关系只需要调整法得知 $(x,y)$ 此时一定被支配。所以需要对上述问题进行分讨，假设我们可以获取所有 $(x,y)$ 点对，考虑对查询的贡献

区间子区间问题的经典套路是把子区间 $[L,R]$ 在二维平面上刻画，而维护二维平面上的一些信息往往是扫描线 $+$ 线段树

暂时不说数据结构如何维护，先来看上面三种情况对子区间的影响。对于某点对来说，合法子区间不好统计，我们转去统计不合法的子区间

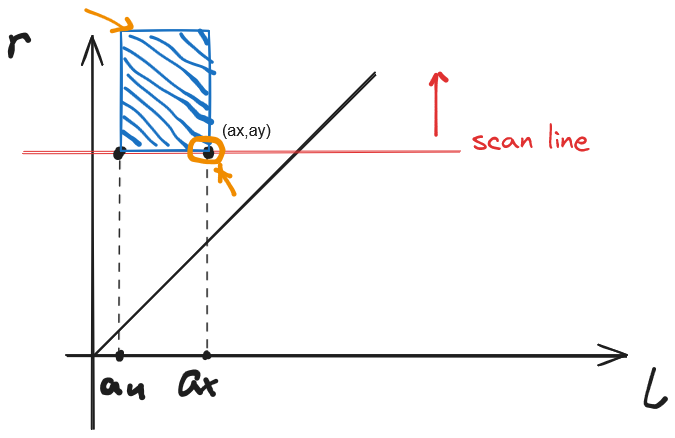
当扫描线扫过 $a_y$ 之后，即 $R \ge a_y$

第一种情况，当 $L \in [a_u+1,a_x]$，点对 $(x,y)$ 无贡献
第二种情况，无事发生
第三种情况，当 $R \in [a_r,a_u-1]$ 而 $L$ 任取，点对 $(x,y)$ 无贡献

简单丢个图上来……

第一种情况的无贡献矩形

第二种情况，无事发生

（这里有一张皇帝的新图片）

第三种情况的无贡献矩形

至于点对数目是 $O(n^2)$ 的，可以运用上题的 dsu on tree 思想弄出支配对

注意到上述三种情况均可被刻画为矩形，题目转化为平面上有若干矩形，求给定矩形范围内 $0$ 的个数

给出一个用到类似吉司机线段树的思想的朴素线段树实现

简单扫描线，显然需要区间加减，求矩形内 $0$ 的个数在线段树上需要维护若干信息，包括区间 $\min$ 值 mn，区间 $\min$ 的个数 mncnt，区间内的 $0$ 个数 sum，区间加的懒标记 tag，以及表示区间 $\min$ 在时间戳上出现的次数 mntag（用于更新 mncnt 的信息）

这里的奇技淫巧还是太有说法了，非常聪明的 mntag

简单说一下具体实现，每次扫描线向上扫一格，就会对 $[1,i]$ mntag 积累 $1$ 次贡献（自增 $1$）

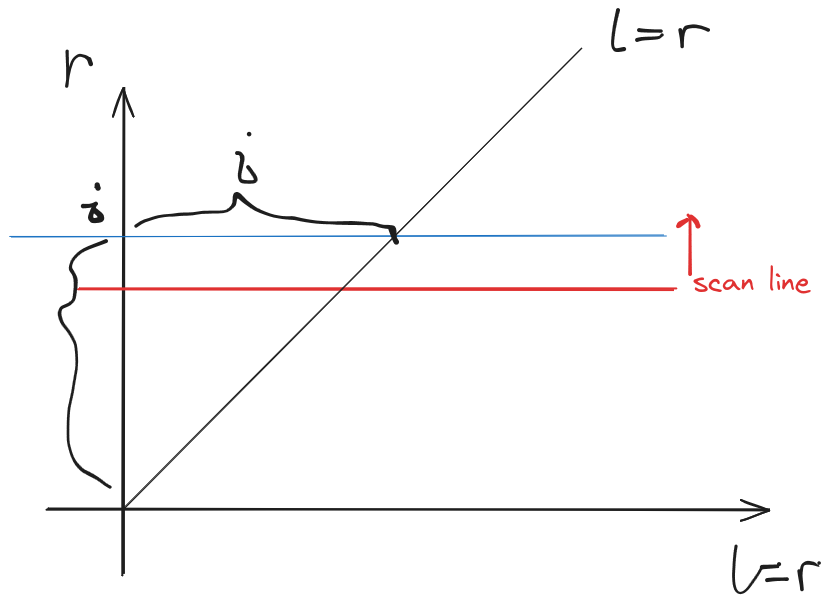
忽略图片右下角的 “$=r$”，莫名其妙的无法删除，也不知道是什么情况

这里的序列不应当是 $[1,n]$，而应当是 $[1,i]$，因为不存在 $l>r$ 的情况

当区间拆分为小区间的时候，我们应当去考察其 $\min $是否为 $0$，只有区间 $\min$ 为 $0$ 的区间才会打上标记

然后考虑 pushdown 的情况，tag 要放在 mntag 之前做，也就是先把区间加这些操作弄掉

做完之后如果左（右）区间的最小值与当前区间的最小值相同，那么这个标记就可以下放

下放标记的同时，要把左（右）区间的 sum 结算一下，显然是 mncnt*mntag

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define vi vector<int>
#define vp vector<pii>
#define vn vector<NODE>
#define pb push_back
#define lwbd lower_bound
#define upbd upper_bound
using namespace std;
const int N=2e5+5;
int n,m,a[N],ans[N];
vi G[N];int siz[N],son[N];
set<int> S[N];
struct NODE{int x,y,w;};
vn p[N];vp q[N];
struct Segment_tree{
	struct node{int l,r,mn,mncnt,mntag,sum,tag;}tr[N<<2];
	inline void build(int u,int l,int r){
		tr[u].l=l,tr[u].r=r,tr[u].mncnt=r-l+1;
		if(l==r)return;
		int mid=(l+r)>>1;
		build(u<<1,l,mid),build(u<<1|1,mid+1,r);
		return;
	}
	inline void maketag(int u,int v){
		tr[u].mn+=v,tr[u].tag+=v;
		return;
	}
	inline void makemntag(int u,int lim,int v){
		if(tr[u].mn==lim)tr[u].sum+=tr[u].mncnt*v,tr[u].mntag+=v;
		return;
	}
	inline void pushdown(int u){
		if(tr[u].tag){
			int v=tr[u].tag;
			maketag(u<<1,v);
			maketag(u<<1|1,v);
			tr[u].tag=0;
		}
		if(tr[u].mntag){
			int lim=tr[u].mn,v=tr[u].mntag;
			makemntag(u<<1,lim,v);
			makemntag(u<<1|1,lim,v);
			tr[u].mntag=0;
		}
		return;
	}
	inline void modify(int u,int ql,int qr,int v){
		int l=tr[u].l,r=tr[u].r;
		if(ql<=l&&qr>=r){maketag(u,v);return;}
		pushdown(u);
		int mid=(l+r)>>1;
		if(ql<=mid)modify(u<<1,ql,qr,v);
		if(qr>mid)modify(u<<1|1,ql,qr,v);
		if(tr[u<<1].mn==tr[u<<1|1].mn)tr[u].mn=tr[u<<1].mn,tr[u].mncnt=tr[u<<1].mncnt+tr[u<<1|1].mncnt;
		else if(tr[u<<1].mn<tr[u<<1|1].mn)tr[u].mn=tr[u<<1].mn,tr[u].mncnt=tr[u<<1].mncnt;
		else if(tr[u<<1].mn>tr[u<<1|1].mn)tr[u].mn=tr[u<<1|1].mn,tr[u].mncnt=tr[u<<1|1].mncnt;
		return;
	}
	inline void update(int u,int ql,int qr,int v){
		int l=tr[u].l,r=tr[u].r;
		if(ql<=l&&qr>=r){makemntag(u,0,v);return;}
		pushdown(u);
		int mid=(l+r)>>1;
		if(ql<=mid)update(u<<1,ql,qr,v);
		if(qr>mid)update(u<<1|1,ql,qr,v);
		tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
		return;
	}
	inline int query(int u,int ql,int qr){
		int l=tr[u].l,r=tr[u].r;
		if(ql<=l&&qr>=r)return tr[u].sum;
		pushdown(u);
		int mid=(l+r)>>1,res=0;
		if(ql<=mid)res+=query(u<<1,ql,qr);
		if(qr>mid)res+=query(u<<1|1,ql,qr);
		return res;
	}
}sgt;
inline void init(int u,int fa){
	siz[u]=1;
	for(int v:G[u]){
		if(v==fa)continue;
		init(v,u);siz[u]+=siz[v];
		if(siz[son[u]]<siz[v])son[u]=v;
	}
	return;
}
inline void ins(int l,int r,int k){
	if(r<k)p[r].pb({1,l,1}),p[k].pb({1,l,-1});
	if(l>k)p[r].pb({k+1,l,1});
	return;
}
inline void dfs(int u,int fa){
	if(son[u])dfs(son[u],u),swap(S[u],S[son[u]]);
	S[u].insert(a[u]);
	for(int v:G[u]){
		if(v==fa||v==son[u])continue;
		dfs(v,u);
		for(int x:S[v]){
			auto it=S[u].lwbd(x);
			if(it!=S[u].end()&&(*it)!=a[u])
				ins(x,(*it),a[u]);
			if(it!=S[u].begin()&&(*prev(it))!=a[u])
				ins((*prev(it)),x,a[u]);
		}
		for(int x:S[v])S[u].insert(x);
		S[v].clear();
	}
	return;
}
signed main(){
	// freopen("in.txt","r",stdin);
	// freopen("out.txt","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=2;i<=n;i++){
		int x;cin>>x;
		G[i].pb(x),G[x].pb(i);
	}
	init(1,0);dfs(1,0);
	for(int i=1,l,r;i<=m;i++)cin>>l>>r,q[r].pb(mkp(l,i));
	sgt.build(1,1,n);
	for(int i=1;i<=n;i++){
		for(auto o:p[i])sgt.modify(1,o.x,o.y,o.w);
		sgt.update(1,1,i,1);
		for(auto o:q[i])ans[o.se]=sgt.query(1,o.fi,n);
	}
	for(int i=1;i<=m;i++)cout<<ans[i]<<'\n';
	return 0;
}

I

题目传送门

对味了，一股 CCF 的味道，又是一套算法捏合题

结论：编号连续的所有结点的 $lca$ 的深度，是所有编号相邻两点的 $lca$ 的深度取 $\min$

证明：
假设这个共同的 $lca$ 由点对 $(L,R)$ 贡献，那么 $L,R$ 一定分属于 $lca$ 的不同子树。考虑那么最不利的情况，$L+1$ 一定与 $L$ 同属于一棵 $lca$ 的子树。同理，不断向下递推……直到 $R-1$ 与 $L$ 同一棵子树，这时候发现 $R-1,R$ 分属于 $lca$ 的不同子树。当最不利的情况依旧说明上述结论正确，则结论一定是正确且具有一般性的

假设我们可以枚举所有的点对 $(x,y)$，那么查询就可以离线扫描线去维护

可以用类似 G 题的方式，搞出支配对，形如一个三元组 $(x,y,v)$，表示支配对 $(x,y)$ 的权值为 $v$

问题转化为：对于每个查询 $[l,r]$，取出所有满足条件 $| [x,y] \cap [l,r] | \ge k$ 的支配对 $(x,y,v)$，对 $v$ 取 $\max$

有交可以分为三类：前缀交、包含交、后缀交。分开做三次扫描线即可，线段树维护区间 $\max$

回到支配对的求解上来，依旧可以是 dsu on tree 那一套流程。不过由于我们这次有相邻这一条件，可以并查集维护连续段——这也保证了支配对数目是 $O(n)$ 的

时间复杂度 $O(n \log n)$，感觉难点在于结论观测和代码实现上

~~怎么还要卡常啊！！！~~

点击查看代码

#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define vi vector<int>
#define vp vector<pii>
#define vn vector<NODE>
#define pb push_back
using namespace std;
const int N=5e5+5;
int n,Q;vi G[N];
int dep[N],son[N],siz[N],dfn[N],tim,rev[N];
struct dsu{
	int fa[N];
	inline void init(){for(int i=1;i<=n;i++)fa[i]=i;return;}
	inline int getfa(int x){return fa[x]==x?x:fa[x]=getfa(fa[x]);}
	inline void merge(int x,int y){
		x=getfa(x),y=getfa(y);
		if(x!=y)fa[y]=x;
		return;
	}
}s1,s2;
struct mod{int l,r,d;}a[N<<1];int tol;
struct que{int l,r,k;}b[N];
vi p[N],q[N];int ans[N];
struct Segment_tree{
	struct node{int l,r,mx;}tr[N<<2];
	inline void pushup(int u){
		tr[u].mx=max(tr[u<<1].mx,tr[u<<1|1].mx);
		return;
	}
	inline void build(int u,int l,int r){
		tr[u].l=l,tr[u].r=r;
		if(l==r){tr[u].mx=0;return;}
		int mid=(l+r)>>1;
		build(u<<1,l,mid),build(u<<1|1,mid+1,r);
		pushup(u);
		return;
	}
	inline void modify(int u,int pos,int v){
		int l=tr[u].l,r=tr[u].r;
		if(l==r){tr[u].mx=max(tr[u].mx,v);return;}
		int mid=(l+r)>>1;
		if(pos<=mid)modify(u<<1,pos,v);
		else modify(u<<1|1,pos,v);
		pushup(u);
		return;
	}
	inline int query(int u,int ql,int qr){
		int l=tr[u].l,r=tr[u].r;
		if(ql<=l&&qr>=r)return tr[u].mx;
		int mid=(l+r)>>1,res=0;
		if(ql<=mid)res=max(res,query(u<<1,ql,qr));
		if(qr>mid)res=max(res,query(u<<1|1,ql,qr));
		return res;
	}
}sgt;
inline int read(){
	int x=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c-'0'),c=getchar();
	return x*f;
}
inline void write(int x){
	if(x>9)write(x/10);
	putchar(x%10+'0');
	return;
}
inline void init(int u,int fa){
	dep[u]=dep[fa]+1;siz[u]=1;dfn[u]=++tim;rev[tim]=u;
	for(int v:G[u]){
		if(v==fa)continue;
		init(v,u);siz[u]+=siz[v];
		if(siz[v]>siz[son[u]])son[u]=v;
	}
	return;
}
inline bool check(int nd,int u){
	return nd>=dfn[u]&&nd<=dfn[u]+siz[u]-1;
}
inline void mrg(int u,int lca){
	int l=s1.getfa(u),r=s2.getfa(u),tmpl=l,tmpr=r;
	while(l>1&&check(dfn[l-1],lca))
		s1.merge(l-1,l),s2.merge(l,l-1),l=s1.getfa(l);
	while(r<n&&check(dfn[r+1],lca))
		s2.merge(r+1,r),s1.merge(r,r+1),r=s2.getfa(r);
	if(l!=tmpl||r!=tmpr)a[++tol]={l,r,dep[lca]};
	return;
}
inline void dfs(int u,int fa){
	for(int v:G[u])
		if(v!=fa)dfs(v,u);
	for(int v:G[u]){
		if(v==fa||v==son[u])continue;
		for(int i=dfn[v];i<=dfn[v]+siz[v]-1;i++)mrg(rev[i],u);
	}
	mrg(u,u);
	return;
}
inline void chkmx(int &x,int y){x=max(x,y);return;}
signed main(){
	// freopen("in.txt","r",stdin);
	// freopen("out.txt","w",stdout);
	n=read();
	for(int i=1;i<=n-1;i++){
		int u=read(),v=read();
		G[u].pb(v),G[v].pb(u);
	}
	init(1,0);s1.init(),s2.init();
	for(int i=1;i<=n;i++)a[++tol]={i,i,dep[i]};
	dfs(1,0);
	Q=read();
	for(int i=1;i<=Q;i++)b[i]={read(),read(),read()};
	for(int i=1;i<=tol;i++)p[a[i].l].pb(i);
	for(int i=1;i<=Q;i++)q[b[i].l].pb(i);
	sgt.build(1,1,n);
	for(int i=1;i<=n;i++){
		for(int x:p[i])sgt.modify(1,a[x].r,a[x].d);
		for(int x:q[i])chkmx(ans[x],sgt.query(1,b[x].r,n));
		p[i].clear(),q[i].clear();
	}

	for(int i=1;i<=tol;i++)p[a[i].r-a[i].l+1].pb(i);
	for(int i=1;i<=Q;i++)q[b[i].k].pb(i);
	sgt.build(1,1,n);
	for(int i=n;i>=1;i--){
		for(int x:p[i])sgt.modify(1,a[x].r,a[x].d);
		for(int x:q[i])chkmx(ans[x],sgt.query(1,b[x].l+b[x].k-1,b[x].r));
		p[i].clear(),q[i].clear();
	}

	for(int i=1;i<=tol;i++)p[a[i].r-a[i].l+1].pb(i);
	for(int i=1;i<=Q;i++)q[b[i].k].pb(i);
	sgt.build(1,1,n);
	for(int i=n;i>=1;i--){
		for(int x:p[i])sgt.modify(1,a[x].l,a[x].d);
		for(int x:q[i])chkmx(ans[x],sgt.query(1,b[x].l,b[x].r-b[x].k+1));
		p[i].clear(),q[i].clear();
	}

	for(int i=1;i<=Q;i++)write(ans[i]),puts("");
	return 0;
}

J

题目传送门

$x$ 级祖先越界无贡献这一件事提示我们去分深度考虑

假设 $x$ 是固定的，显然我们可以预处理出每个结点的 $x$ 级祖先，跑一遍区间数颜色

这个做法是否可以推广？

由题意，互相影响的点一定在同一个深度。进一步地，如果把 $x$ 级祖先相同的点放在一个集合，那么当 $x$ 向上扫描的时候相当于要合并若干集合

注意到将一个点丢到一个集合中，至多只会修改两个 pre，而如果我们在合并集合使用启发式合并就相当于完成带 $O(n \log n)$ 次修改的在线二维数点

这玩意不就是离线三维数点吗，CDQ 简单维护，时间复杂度是三支 $\log$

问题转化为如何把向集合插入元素的环节离线下来

那还废什么话，直接上 stl 呗（包括但不限于 set 和 vector）

代码还没来得及写，要下班了

又双叒叕上班了，荣升为大常数选手

卡常技巧：如果你在 QOJ 上被卡常（包括但不限于 41pts/77pts）

尝试把 sort 替换成 stable-sort。据说 sort 是基于快排的排序，在对一些结构体或者 pair 之类的 stl 常数比较神秘；而 stable-sort 是基于归并排序，所以可能在 CDQ 的分治结构中效果更佳
QOJ 可以手动内联和 O2 优化
如果你使用了 vector，建议将 push_back 替换成 emplace_back
高效的输入输出
可以不建双向边，让 vector 的内存压力小一点
这道题无需 long long，请删除你的无效 #define int long long
不要出现 memset 等类似的大常数选手
CDQ 内部建议双指针维护，不要莫名其妙地多出一支 $\log$

贴一份峰值时间 2491ms 的代码

点击查看代码

#pragma GCC optimize(2,"Ofast","inline")
#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
#define mkp make_pair
#define vi vector<int>
#define vp vector<pii>
#define vn vector<NODE>
#define pb emplace_back
#define lwbd lower_bound
using namespace std;
const int N=1e6+2;
int n,m,rt,ans[N];vi G[N];
int dep[N],siz[N],son[N],dfn[N],tim,rev[N];
set<int> S[N];vp vec[N];
struct NODE{int x,y,z,id,o;}a[N*3];int tol;
struct BIT{
	int c[N];
	int lb(int x){return x&(-x);}
	void clr(int x){
		for(int i=x;i<=n;i+=lb(i))c[i]=0;
		return;
	}
	void add(int x,int v){
		for(int i=x;i<=n;i+=lb(i))c[i]+=v;
		return;
	}
	int ask(int x){
		int res=0;
		for(int i=x;i;i-=lb(i))res+=c[i];
		return res;
	}
}bit;
int read(){
	int x=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c-'0'),c=getchar();
	return x*f;
}
void write(int x){
	if(x>9)write(x/10);
	putchar(x%10+'0');
	return;
}
void init(int u,int fa){
	dep[u]=dep[fa]+1,siz[u]=1,dfn[u]=++tim,rev[tim]=u;
	for(int v:G[u]){
		init(v,u);siz[u]+=siz[v];
		if(siz[v]>siz[son[u]])son[u]=v;
	}
	return;
}
void dfs(int u){
	for(int v:G[u]){
		if(v==son[u])continue;
		dfs(v);
		for(int i=dfn[v];i<=dfn[v]+siz[v]-1;i++)S[dep[rev[i]]].erase(rev[i]);
	}
	if(son[u])dfs(son[u]);
	for(int v:G[u]){
		if(v==son[u])continue;
		for(int i=dfn[v];i<=dfn[v]+siz[v]-1;i++){
			int x=rev[i],d=dep[x];auto it=S[d].lwbd(x);
			if(it!=S[d].end())vec[*it].pb(mkp(x,d-dep[u]));
			if(it!=S[d].begin())vec[x].pb(mkp(*--it,d-dep[u]));
			S[d].insert(x);
		}
	}
	S[dep[u]].insert(u);
	return;
}
bool cmp(pii s,pii t){return s.fi>t.fi;}
bool cmp1(NODE s,NODE t){
	if(s.x!=t.x)return s.x>t.x;
	if(s.y!=t.y)return s.y<t.y;
	if(s.z!=t.z)return s.z<t.z;
	return s.o<t.o;
}
bool cmp2(NODE s,NODE t){
	if(s.y!=t.y)return s.y<t.y;
	if(s.z!=t.z)return s.z<t.z;
	return s.o<t.o;
}
void cdq(int l,int r){
	if(l>=r)return;
	int mid=(l+r)>>1;
	cdq(l,mid),cdq(mid+1,r);
	stable_sort(a+l,a+mid+1,cmp2),stable_sort(a+mid+1,a+r+1,cmp2);
	int j=l;
	for(int i=mid+1;i<=r;i++){
		if(!a[i].o)continue;
		while(j<=mid&&a[j].y<=a[i].y){
			if(!a[j].o)bit.add(a[j].z,a[j].id);
			j++;
		}
		ans[a[i].id]-=bit.ask(a[i].z);
	}
	for(int i=l;i<=mid;i++)
		if(!a[i].o)bit.clr(a[i].z);
	return;
}
int main(){
	n=read(),m=read();
	for(int i=1,x;i<=n;i++){
		x=read();
		if(x)G[x].pb(i);
		else rt=i;
	}
	init(rt,0);dfs(rt);
	for(int i=1;i<=n;i++)vec[i].pb(mkp(i,dep[i]));
	for(int i=1;i<=n;i++){
		stable_sort(vec[i].begin(),vec[i].end(),cmp);
		int mn=n+1;
		for(auto x:vec[i]){
			if(x.se>=mn)continue;
			if(mn<=n)a[++tol]={x.fi,i,mn,-1,0};
			a[++tol]={x.fi,i,x.se,1,0};
			mn=x.se;
		}
	}
	for(int i=1,l,r,x;i<=m;i++){
		l=read(),r=read(),x=read();
		a[++tol]={l,r,x,i,1};
		ans[i]+=r-l+1;
	}
	stable_sort(a+1,a+tol+1,cmp1);
	cdq(1,tol);
	for(int i=1;i<=m;i++)write(ans[i]),puts("");
	return 0;
}

后记

世界孤立我任它奚落

完结撒花！

posted @ 2025-09-17 14:14 sunxuhetai 阅读(25) 评论(0) 收藏举报

刷新页面返回顶部

浮海沉天

笔名：云落

9.16 jsy 支配对选讲

前言

正文（加餐）

A

B

C

D

E

F

G

H

I

J

后记

公告