9.12 lyc CF 杂题选讲
前言
业精于勤荒于嬉,行成于思毁于随
正文(加餐)
杂题选讲
CF1637F
注意到建塔一定建在叶子上(调整法易证),然后容易想到以 \(h\) 最大的结点为根
把根拎出来之后,在钦定根合法的情况下,其它的所有非根结点只需保证自己的子树内有关键点即可,这也是确定根结点的原因
非根结点对答案的贡献是简单的。设当前访问到 \(u\) 结点,\(u\) 子树内(不含 \(u\))的关键点最大权值为 \(mx\),则有如下两种情况:
- \(h_u \le mx\),显然对答案毫无贡献,直接忽略
- \(h_u>mx\),对答案的贡献是 \(h_u-mx\),并把 \(mx\) 调整至 \(h_u\)
让根合法也不难做,维护根节点每棵子树返回的最大值,取所有最大值中最大的和次大的两个,分别记作 \(mx\) 和 \(cmx\),那么对答案的贡献就是 \(\max(0,h_{rt}-mx)+\max(0,h_{rt}-cmx)\)
这个贡献计算方式是不失一般性的,即便 \(rt\) 在只有一个儿子的时候也适用(此时 \(cmx=0\),后半部分的贡献就是 \(h_{rt}\),相当于令 \(rt\) 成为一个关键点)
剩下的代码实现就没什么了,依照上述分析模拟即可
CF468D
set 这玩意还是太强大了,直接把代码实现难度降低了好几个 level
不喜欢无根树,要有根树,所以有了根。钦定根结点的操作是完全与答案无关的,所以根结点可以由我们自由抉择。另一方面,有了根之后,可以把式子拆成
观察到前面两项是个定值,所以对于我们钦定的根结点,想要卡到最大值就一定是让后面这一项最小
不妨设根结点为树的重心,根据类似摩尔投票的性质,我们总可以构造出一种方案使得对于任意的 \((i,p_i)\),有 \(lca(i,p_i)=rt\)(换言之,最后一项为 \(0\))
Q:如何想到钦定根为树的重心的?
A:三个角度。一是自由决策根结点,根据套路可以先想一想重心;二是上面那个式子推出来之后可以去想 \(lca=rt\) 的性质;三是维护的是路径信息,就有一种淀粉质的感觉(虽然八竿子打不着),思维发散一下就好了
答案已经显然了,接下来是构造方案,一个基本约束是 \(i,p_i\) 分属于根的不同子树,或者存在一个为根
字典序问题,显然从小到大贪心去做,假设我们当前要给 \(x\) 找一个 \(p_x\)
首先,是否有合法方案存在,或者说合法方案存在的判定条件是什么?
为了方便表述,在 \(x \to p_x\) 的一组匹配中,我们称 \(p_x\) 为入点,\(x\) 为出点
记 \(in_u\) 表示 \(u\) 子树中未匹配的入点数目,\(out_u\) 表示 \(u\) 子树中未匹配的出点数目,方案存在的充要条件是:
对于任意的 \(rt\) 的子结点 \(i\),满足
式子太丑陋了,转化为
不等号右边可以理解为,剩余未匹配的数目。可以简单转化为总匹配数目刨除已匹配数目,由于我们枚举到 \(x\),所以已匹配数目就是 \(x-1\),总匹配数目显然为 \(n\),那么上面的式子又可以写成——
考虑用 set 去记录所有的 \(in_i + out_i\)
如果枚举到 \(x\) 的时候触发了取等情况,那么 \(p_x\) 就只能在 \(i\) 子树中选取编号最小的。因此,我们还需要再来一个 set 取存储每个子树中剩余未匹配的编号
反之,如果没有触发取等情况,那么 \(p_x\) 就可以任选。显然取出每个子树未匹配的编号最小值,再给它塞到一个 set 里去维护。细节上,为了保证不会出现同子树的情况,我们还需要维护 bel[u] 表示 \(u\) 隶属于哪棵子树
剩下的就没了,匹配一组之后在 set 上作相应修改即可
CF1879D
切入点一:经典的贡献计算问题,肯定去想区间批量处理,并且容易想到前缀差分
切入点二:贡献里面带一个异或值,考虑拆位统计
前面两步第一反应之后,问题转化为,对于 \(k\) 组 \(01\) 序列 \(a\),计算下列式子:
考虑批量处理所有以 \(r\) 为右端点的答案,换言之,扫描右端点 \(r\),动态维护答案
为了方便表述,记 \(f(l,r)=\oplus_{i=l}^{r} a_i\)
具体地,记 \(c0,c1,s0,s1\),含义如下:
- \(c0\) 表示 \(\sum \limits_{1 \le j \le i}[f(j,i)=0]\);
- \(c1\) 表示 \(\sum \limits_{1 \le j \le i}[f(j,i)=1]\);
- \(s0\) 表示 \(\sum \limits_{1 \le j \le i}[f(j,i)=0](i-j+1)\);
- \(s1\) 表示 \(\sum \limits_{1 \le j \le i}[f(j,i)=0](i-j+1)\)
典中典之计算右端点 ++ 之后带来的变化量
首先就是由于 \(i \to i+1\),所以 \(s0,s1\) 都会变化,变化量分别为 \(c0,c1\)
然后就是看当前 \(a_i\) 的 \(0/1\) 情况*
- 如果 \(a_i=0\) 就只会影响 \(c0,s0\);
- 如果 \(a_i=1\) 就需要先
swap(s0,s1),swap(c0,c1),再影响 \(c1,s1\)
贡献给当前答案的当然是 \(s1\),不过不要忘记拆位的权重和取模问题
CF1706D2
观测题解发现是清一色的利用数论分块的思想?
本人这个过了,但是时间复杂度双 \(\log\),不知道有没有 hack 或者正确性的证明
先让 \(p_i=k\),计算出一个 \(ans\) 的可行解
注意到贡献计算式子和 \(a\) 的顺序无关,不妨钦定其有序
然后容易想到枚举最小值 \(mn\),然后去最小化最大值
如果我们想最小化 \(\lfloor \frac{a_i}{p_i} \rfloor\) 的最大值,在 \(a_i\) 给定的情况下,一定是让 \(p_i\) 越大越好
不过需要满足下面的限制
为了方便表述,记函数 \(f(a_i,mn)\) 表示在给定 \(a_i,mn\) 且保证合法的情况下,\(p_i\) 的最大取值
可能题解区这个时候就枚举 \(\lfloor \frac{a_i}{p_i} \rfloor\) 了,但为什么不直接去枚举 \(p\) 捏?
注意到,在 \(mn\) 固定的时候,\(f(a_i,mn)\) 一定会在序列上会拆分成不超过 \(\min(\frac{a_n}{mn},k)\) 个连续段的形式。而且由于已经钦定了序列 \(a\) 有序,那么对每个连续段,只有连续段的右端点才可能对最大值造成贡献
时间复杂度应当是找连续段右端点 \(\times\) 连续段总数
前面的可以简单 lower_bound 解决,后面看似 \(O(n^2)\),实则调和级数
总时间复杂度双 \(\log\),而且代码短,空间常数小(基本就没有空间常数)
不会被神秘的 \(62.5\)MB 的空间限制卡掉
CF1699E
又是一道最小化极差的问题,依旧考虑枚举最小值,最小化最大值
当然,由题意分析,肯定从大到小枚举最小值是符合常理的
为了方便表述,记 \(f_i\) 表示数 \(i\) 在所有不分解出比 \(<mn\) 的因子的分解方式中,最大因子最小的那一个
根据上述定义,当 \(mn\) 固定的时候,\(mx\) 可以表示为
问题转化为对于每一个确定的 \(mn\),求出所有的 \(f_x\)
考虑 DP 及其转移,初始化 \(f_i=i\)
注意到 \(mn\) 在更新的时候,会影响到所有 \([mn^2,m]\) 范围内 \(mn\) 的倍数,因为可以分解出一个因子 \(mn\)
所以,枚举上述受影响的数 \(i\),有转移方程
啧,容易发现,受影响的数是调和级数量级的,也就是最多转移 \(O(m \ln m)\) 次,时间复杂度很有保证
然而,要求的是 \(x \in S f_x\),显然不能遍历 \(f\) 数组求最大值
观察到枚举最小值,快速找最大值的操作本质上与双指针类似,并且容易证明其单调性
所以可以维护一个 \(f\) 的桶数组,由于最大值随着最小值的递减而单调不降,所以在桶数组上记录指针可以同时保证正确性与时间复杂度
代码实现上注意多测清空,DP 初始化的问题即可
CF1691F
换根 DP 是显然的,先来看根确定的情况
记 \(f_u\) 表示 \(u\) 子树内的答案,有转移方程
不难理解,首先所有的 \(f_v\) 肯定会直接贡献给 \(f_u\),然后只需要考虑 \(lca\) 为 \(u\) 的情况。在 \(u\) 子树中任选 \(k\) 个点,然后刨除 \(k\) 个点在同一棵 \(v\) 子树中的情况,把 \(siz_u\) 作为权值乘上就没问题了
然后开始换根,这坨式子并不好看,但是可以大致分为与 \(u\) 有关,与 \(v\) 有关,与 \(u,v\) 都有关三大类
因为一次换根只会对 \(siz\) 产生影响,只需要把 \(\sum {siz_v \choose k}\) 提前预处理出来,剩下的可以按照转移式子直接做
CF1770E
疑似是“特殊——一般”的巅峰之作,推广的过程相当精彩
假设蝴蝶翅膀断了,没有飞行的功能,考虑如何去计算答案
你发现可以枚举每条边(有点换根 DP 那意思?),维护被这条边割开两个连通块中各有多少只蝴蝶。假设某一联通块的蝴蝶数目为 \(x\),那么这条边的贡献就是 \(x(k-x)\),据此也可以计算出总的期望,即
其中 \(sum_u\) 表示 \(u\) 所在连通块的蝴蝶数目
好了,现在蝴蝶的翅膀痊愈了,考虑飞行的情况
注意到一条边只会经过蝴蝶一次,而且最多只能经过一只蝴蝶,进一步地只会在边的两端产生蝴蝶的修改,所以对 \(sum_u\) 的影响最多只有 \(1\)
我们把飞行的事件加进来,显然 \(sum_u\) 把连通块内的蝴蝶数目修改为连通块内期望的蝴蝶数目
不妨设 \(p_u\) 表示 \(u\) 的位置存在蝴蝶的概率,要计算 \((u,v)\) 的贡献
现在有 \(p_u,p_v\),考虑 \(u \to v\) 飞行之后去更新 \({p'}_u,{p'}_v\)
-
若 \(u,v\) 都有蝴蝶,则 \({p'}_u=p_up_v\)
-
若 \(u,v\) 都没有蝴蝶,则 \({p'}_u=0\)
-
若 \(u\) 有而 \(v\) 无,则 \({p'}_u=\frac{p_u(1-p_v)}{2}\)
-
若 \(u\) 无而 \(v\) 有,则 \({p'}_u=\frac{p_v(1-p_u)}{2}\)
所以对于 \(u \to v\) 飞行事件,\(u\) 还留有蝴蝶的概率就是上述四种情况的和,简单计算得 \({p'}_u = \frac{p_up_v}{2}\)
当然,在这个事件上,\(v\) 与 \(u\) 是对称的,所以有 \({p'}_v={p'}_u=\frac{p_up_v}{2}\)
我们已经学会了概率的更新,那么贡献的计算捏?
按照上面四种情况继续分讨嘛,根据全期望公式和期望的线性性,随便维护一下就好了嘛
CF1635F
清新结论题,可能思考过程更有参考价值叭……
为了方便表述,定义 \(L_i,R_i\) 如下:
结论:成为答案的一定是 \((i,R_i)\) 或者 \((L_i,i)\)
证明略
后续操作经典扫描线加线段树(当然也可以写后缀 \(\min\) 的树状数组)
以下是猜结论的思维过程……
猜结论没什么技巧,整套流程都很感性,建议酌情食用
当固定左端点 \(i\) 的时候,注意到 \(j\) 近小绝对是上上签。其次是远小或者近大,而远大可以大胆猜测其不构成答案
显然接下来要考察远小,所有满足远小这一概念的 \(j\) 一定会决出一个最优的,而如果把这些可能的 \(j\) 按 \(x_j\) 排序,有可能造成贡献的一定是一条 \(w_j\) 单减的序列
这个感性理解也可以推广到近大这一类中
进一步地,把可能成为答案的 \(j\) 投射到 \(xOw\) 的二维平面上
展示一张草稿图……画风略丑
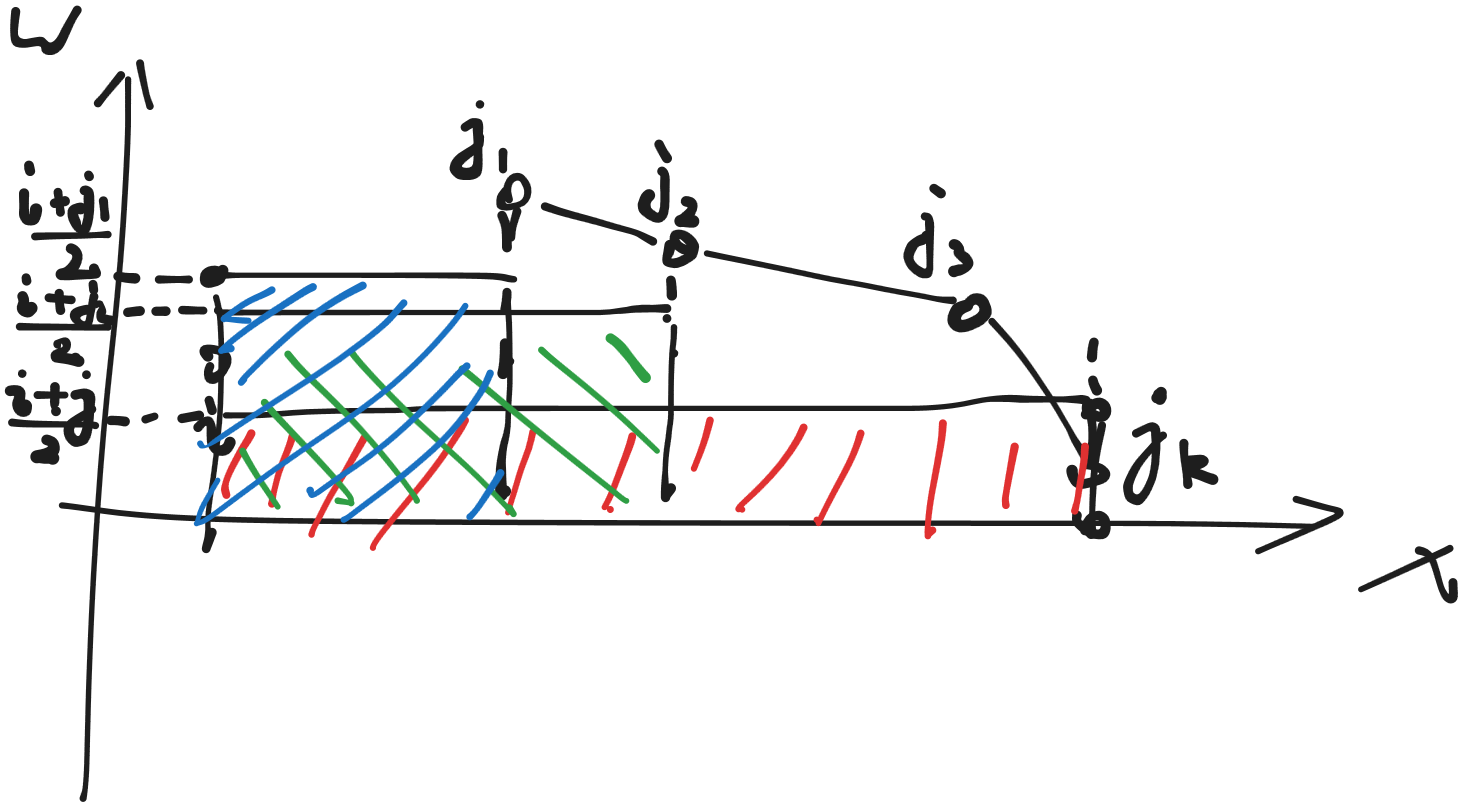
然后开始关注 \(j_k\) 这个点,在 \(i\) 右侧第一个满足 \(w_j \le w_i\) 这个点
斗胆断言,\(j_k\) 就是 \(i\) 为左端点的最优解,因为它是第一个拉低把长方形的宽拉到 \(w_i\) 以下的(长方形面积显然是贡献式子,宽这里取 \(\frac{w_i+w_j}{2}\),图上标错了)
然后弄了几组 hack,最优解结论破产
但没有完全破产,因为前面有钦定 \(i\) 为左端点的,局限性很强。而且观测到 hack 数据总可以通过采用相同的结论而更换固定点的方式得到答案
所以 hack 了,但没完全 hack
结论弄出来之后,补充完善一下,就是前面的那个形式化表述,很幸运,这是正确的
CF1691E
???什么鬼,讲板子题?
连通块这种概念一出来一定是并查集……而且你发现区间交的形式一定是坐标的顺序有关,所以排序扫描线呗。具体地,按右端点排序
然后你对每种颜色维护类似单调栈的结构,栈顶应当是当前右端点最靠右的线段
每次新插入一条线段,把异色栈顶取出,快速判断线段是否相交,然后并查集合并
额,直接模拟即可?注意多测清空就好了
CF1854C
期望好题
根据期望的线性性,答案可以转化为 \(\sum E(S_i)\),其中 \(E(S_i)\) 表示把 \(S_i\) 删除的期望步数
你发现 \(E(S_i)\) 只和 \(E(S_{i+1})\) 有关,因为在 \(S_i\) 前面的都可以被 \(S_i\) 吃掉,而在 \(S_{i+1}\) 后面的都会被 \(S_{i+1}\) 碰撞,灵魂交换后被删除
考虑根据上述分析写出 DP,记 \(f_{i,j}\) 表示前值在 \(i\),后值在 \(j\),而 \(i\) 追上 \(j\) 的期望步数,转移方程形如
这个 \(\frac{1}{2}\) 相当精辟,重点就是在于我们其实并不关心其它点的情况
答案是好计算的,对所有的 \(f_{a_i,a_{i+1}}\) 求和之后,再加上 \(S_n\) 走出边界的步数即可
形式化地,有
代码疑似不超过 \(20\) 行
CF1610E
dottle 说,这类题型都有部分显著的特点,叫做子结构问题
你可能会在题面中看到如下叙述:“对于 xxx,我们称 xxx 是“好的”,当且仅当……”
后面那个……往往比较繁琐,令人摸不着头脑。因此,分析的时候从条件切入,考虑去寻找或者猜测一个满足……条件的子结构,并且这个子结构会让我们身心愉悦
可能干说没什么感觉,结合这个题来说吧
题面中有这样一句话:我们称一个长度为 \(m\) 的整数数组 \(b_1,b_2,\dots,b_m\) 是坏的,当且仅当它存在至少一个非空子序列是糟糕的,否则称其为好的
非空子序列这种东西根本没有办法去维护,其规模是指数级的。而子序列的结构又是板上钉钉不容更改的,So……?
《注意到》我们可以缩减子序列的长度以达到减少条件规模的目的
比如,我们认为,如果一个序列中不存在长度为 \(3\) 的非空子序列是糟糕的,那么这个序列就是好的
上面这一坨是我们拍脑袋拍出来的,有没有正确性保证需要再议,不过这也的确提供了一个不错的思考方式
接下来试图证明上述结论和题目描述等价
必要性显然,充分性考虑反证法
证明:
假设存在反例,则反例一定满足,存在某个长度 \(>3\) 的子序列是糟糕的,但不存在长度 \(=3\) 的长度是糟糕的
我们把这个不合法的子序列提取出来,记作 \(c_1,c_2,\dots,c_k\)。根据题意,这个序列排序之后一定是满足中位数的值要大于序列的平均值的。为了方便表述,记 \(m=\lceil \frac{k}{2} \rceil\),形式化地,有
同样地,由于该序列不存在长度 \(=3\) 的糟糕子序列,所以其也应满足相关性质。形式化地,对于任意的 \(i,j,x\),满足
你考虑对序列 \(c\) 进行一个首尾配对,结合上式,对于任意的 \(x\),有
不妨令 \(x=m\),上述式子可以写成
现在我们对每一对 \(i\),进行首尾配对,并求和,得到
整理一下,有
你会发现与前面中位数严格大于平均值的结论是矛盾的,故假设不成立,结论得证
所以条件就被我们成功缩小了,然后这个问题变得非常简单。删除元素不好做,考虑加尽可能多的元素
重点:钦定初始的 \(x,y\) 是两个极值,然后在极值之间加入元素
你注意到每次在已有 \(x,y\) 的情况下新加入一个 \(z\)(此时有 \(x \le y \le z\)),需要满足
规模缩半,显然对于固定的 \(x,y\),插入操作次数上限为 \(O(\log V)\) 次
\(x,y\) 不需要都枚举,枚举 \(x\),容易发现一个贪心性质,即 \(y\) 越大越好,不妨取序列最大值
一个小细节,在取等的条件中,只有最小值 \(x\) 可以多次出现,否则就会出现糟糕的子序列形如 \(\{ x,k,k \}\)
剩下的直接模拟即可
CF1620F
好题
啧,出现一个逆序对,就会有一条边。二分图的判定条件是是否存在奇环,显然是又是一个与子序列相关的判定条件……
那么还是仿照上题结论,考察一些性质较优的子结构,比如长度为 \(3\) 的子序列
你发现一个序列中存在长度为 \(3\) 的下降子序列,那么这个序列一定不合法
上面这句话说明了必要性,充分性有木有?
dottle:当你用一个必要条件大量排除了很多不合法的子序列,就可以去思考这个条件是否也是充分的
根据 Dilworth 定理,如果一个序列不存在长度为 \(3\) 的下降子序列,那么其肯定可以划分为两个不交的最长上升子序列
那么上升子序列内部没有任何边相连,显然你已经构造出了一种二分图,所以该序列一定是可二分的,进而说明了结论的充分性
构造方案似乎可以简单贪心,不多赘述
CF1750F
后面的题都很有 CF 特色,吃点神秘 DP 总归是不错的
计数题,并且很难组合数去做,显然 DP。不过 DP 之前,我们要求去判定条件进行分析。具体地,合法结构不好描述,转而描述不合法的结构
一个串是不合法的,当且仅当他可以被拆分为若干 \(01\) 相间的连续段,其中对于每个 \(0\) 连续段,与之相邻的两个 \(1\) 连续段的长度之和 \(\le\) 当前 \(0\) 连续段的长度
根据这个连续段长度的情况,我们对无法继续操作的串进行考察,并设计出如下 DP
记 \(f_{i,j}\) 表示串长为 \(i\),钦定两端为 \(1\),最后一个 \(1\) 连续段的长度为 \(j\) 的方案数,答案显然是 \(f_{n,n}\)
考虑转移。显然不合法的情况和合法的情况不能一块做,要分开转移
合法串转移
\(f_{i,i}\) 可以简单容斥,转移方程形如
前面的 \(2^{i-2}\) 好理解,即总方案数;后面的 \(\sum\) 表示不合法的方案数,而对于不合法的情况,其最后的 \(1\) 连续段长度至多到 \(\lfloor \frac{i-1}{2} \rfloor\),所以有如上转移方程
不合法串转移
\(f_{i,j}\) 转移比较朴素,枚举最后一个 \(0\) 连续段的长度,再枚举倒数第二个 \(1\) 的连续段长度,简单求个和即可
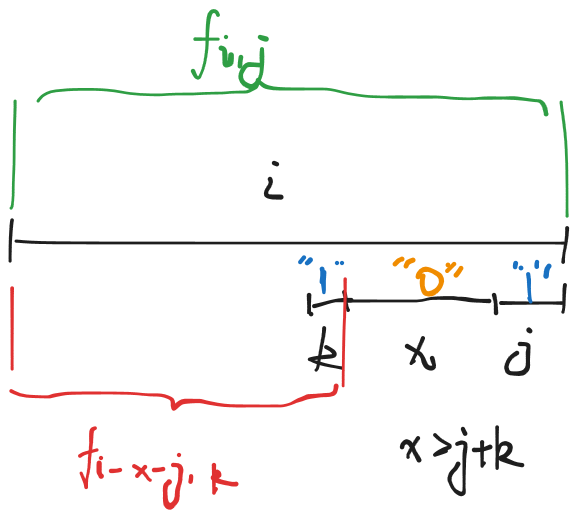
具体地,转移方程形如
上式结合着下图去看可以辅助理解,写代码的话,循环上界还得自己弄一弄,调完之后不带艾弗森括号就舒服了
不过这玩意过不了,毕竟 \(O(n^4)\) 摆在这里,不过显然可以前缀和优化,直接干掉两层 \(\sum\),宣告撒花!
CF1693D
需要较为强大的拍脑袋能力
题意相当于对满足如下条件的连续段计数
- 可以划分为一个单调递减子序列和一个单调递增子序列
计数问题有点困难,先思考如何判定上述条件
记 \(f_{i,0}\) 表示考虑到第 \(i\) 位且第 \(i\) 位在单增序列中,单减序列的末尾元素最大值;记 \(f_{i,1}\) 表示考虑到第 \(i\) 位且第 \(i\) 位在单减序列中,单增序列的末尾元素最小值
想出这个 DP 状态的估计都是吃 deepseek 长大的
初值肯定都是 \(+ \infty/-\infty\)
那么如果一个连续段合法,当且仅当 \(f_{n,0} \neq -\infty \lor f_{n,1} \neq +\infty\)
转移应该就是简单的 \(f_{i-1} \to f_{i}\),单次 \(O(1)\),总时间复杂度 \(O(n)\)
先不说具体地转移方程如何刻画,先来考虑计算答案
枚举 \(l,r\) 然后跑上面的 DP 肯定有正确性,但 \(O(n^3)\) 肯定过不了
注意到当固定左端点的时,随着右端点的向后扩展,限制只会越来越严格。所以你只需要线性扫过去,记录最极限的合法情况,然后批量统计,可以做到 \(O(n^2)\)
燃尽了,还有一个 \(O(n)\) 消不掉。拼尽全力,无法战胜……
回过头来思考这个 DP 的转移实质,发现只有 \(i-1\) 才会对 \(i\) 造成贡献。这意味着,如果我们从大到小枚举左端点,每次左端点平移一格的时候,是不是可能会有一段后缀的 DP 值不受影响?
换言之,是不是只有一部分的 DP 值会随左端点平移而改变?那我们只修改会改变的部分就好了嘛,剩下不变的部分直接 break 掉
把这个“剪枝”优化加上去就是线性的了,至于为什么嘛,还得看具体的转移方程
转移方程推导
简单分类讨论一下,现在由 \(i-1\) 贡献到 \(i\)
假设 \(i-1\) 在单增序列中——
-
若 \(a_i\) 在单增序列中,则要求 \(a_i>a_{i-1}\),转移方程形如 \(\text{chkmx} (f_{i,0},f_{i-1,0})\)
-
若 \(a_i\) 在单减序列中,则要求 \(a_i<f_{i-1,0}\),转移方程形如 \(\text{chkmn}(f_{i,1},a_{i-1})\)
假设 \(i-1\) 在单减序列中——
-
若 \(a_i\) 在单减序列中,则要求 \(a_i<a_{i-1}\),转移方程形如 \(\text{chkmn} (f_{i,1},f_{i-1,1})\)
-
若 \(a_i\) 在单增序列中,则要求 \(a_i>f_{i-1,1}\),转移方程形如 \(\text{chkmx}(f_{i,0},a_{i-1})\)
收工!!!
时间复杂度分析
我们断言,对于每个 \(i\),其 DP 值最多只会被更新 \(7\) 次
具体地,考虑 \(f_{i,0}\) 以及下图的结构

\(j\) 是 \(i\) 之前第一个满足 \(a_{j}>a_{j+1}\) 的点
对于某个包含 \(i\) 的连续段来说,你发现 \(f_{i,0}\) 有且至多有四种取值……
-
若不存在这样的 \(j\),若 \(f_{i,0}\) 可以是 \(+\infty\)
-
若前面的情况已经无法构造合法方案,\(f_{i,0}=-\infty\)
-
若 \(j\) 在单增序列中,则 \(j+1\) 一定在下降序列中,\(f_{i,0}=a_{j+1}\)
-
若 \(j\) 在单减序列中,则 \(j+1\) 无所谓,\(f_{i,0} = a_{j}/a_{j+1}\)
所以对于一个 \(i\) 来说,\(f_{i,0/1}\) 共计八种情况,也就是说只会被更新 \(7\) 次
那么均摊下来时间复杂度就没问题咯!
代码实现应该不难,反正云落就写了 \(30\) 行
后记
世界孤立我任它奚落
完结撒花!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号