1.15 下午-矩阵初步

前言

勿让将来，辜负曾经

也是最后一章了，云落想咕咕咕咕咕咕咕掉咯！

哎，云落有个强迫症，如果要贴代码的话必须自己重新敲，但是最近确实有点忙，没时间敲（重点是漫长的 debug），所以代码就咕咕咕了

正文

怎么感觉矩阵相关问题都和矩阵本身没有什么太多关系？

知识点

矩阵，数学里的定义更为严谨一些，不过放在 oi 中，就是二维数组

矩阵乘法

左行右列。给定 \(P \times M\) 的矩阵 \(A\) 和 \(M \times Q\) 的矩阵 \(B\)，记 \(A \times B\) 的结果为矩阵 \(C\)，有：

\[C_{i,j} = \sum_{k=1}^{M} A_{i,k}B_{k,j} \]

显然，矩阵 \(C\) 的尺寸为 \(P \times Q\)

矩阵乘法没有交换律，有结合律

矩阵快速幂

其实就是将矩阵乘法中的乘号重载之后直接套用快速幂模板即可

引入：单位矩阵

单位矩阵就是主对角线 （所有 \(A_{i,i}\)）上全是 \(1\)，其余位置都是 \(0\) 的方阵

一般我们默认参与矩阵快速幂的矩阵都是方阵（否则很难保证矩阵乘法有意义）

动态 DP

动态维护树上最大权独立集问题。说人话就是带修的没有上司的舞会

首先要将一个点，虽然说这个算法比较长，但是整个思维过程相当自然，所以云落个人认为这东西甚至比 KMP 好理解

先简单解决一下静态问题，记 \(f_{u,0/1}\) 表示 \(u\) 结点 不选/选 的子树内的答案，在叶子结点上初始化

转移方程形如：

\[f_{u,0} = \sum_{v \in son_u} \max (f_{v,0},f_{v,1}) \newline f_{u,1} = a_u + \sum_{v \in son_u} f_{v,0} \]

时间复杂度 \(O(n)\)

但是现在出现了一个动态的单点修改问题，比较朴素的是每次修改之后重新去扫一遍 DP。如果有 \(q\) 次操作，时间复杂度是 \(O(n \times q)\) 的，显然不优

然后注意力惊人一下，我们发现，对于一次单点修改操作，受到影响的仅有本身以及其返祖链上的所有结点的 DP 值

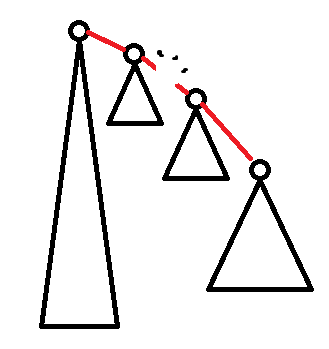
维护链修改，子树查询（虽然是全树查询，但是可以视作以 \(1\) 为根的子树），考虑树链剖分

如果我们能快速地维护一条重链上的 DP 值，那么这个问题就解决了。不过，目前比较优秀的性质就只有重链的 DFS 序连续

所以回归原来这个式子，我们试图在在原有的式子上发掘一些新的性质

\[f_{u,0} = \sum_{v \in son_u} \max (f_{v,0},f_{v,1}) \newline f_{u,1} = a_u + \sum_{v \in son_u} f_{v,0} \]

结合重链剖分，容易想到轻重儿子分开处理——引入两个变量

记 \(g0\) 表示对于一个子树 \(u\)，结点 \(u\) 不选，且不考虑重儿子的贡献的答案；记 \(g1\) 表示对于一个子树 \(u\)，结点 \(u\) 选，且不考虑重儿子的贡献的答案

于是乎上面的式子的求和号就没咯

\[f_{u,0} = g0 + \max(f_{son_u,0},f_{son_u,1}) \newline f_{u,1} = g1 + f_{son_u,0} \]

简单变形

\[f_{u,0} = \max(g0 + f_{son_u,0},g0 + f_{son_u,1}) \newline f_{u,1} = \max(g1 + f_{son_u,0},- \infty) \]

写到这里基本上就差不多咯！注意到里面的转移式可以写成一个广义矩阵乘法的形式，形如：

\[\begin{equation} \begin{gathered} &\begin{bmatrix} g0 & g0 \newline g1 & -\infty \end{bmatrix} & \times &\begin{bmatrix} f_{son_u,0} \newline f_{son_u,1} \end{bmatrix} & = &\begin{bmatrix} f_{u,0} \newline f_{u,1} \end{bmatrix} \end{gathered} \nonumber \end{equation} \]

剩下的就是对于每个结点构造矩阵，然后矩阵加速就结束了

一题一解

T1 【模板】矩阵快速幂（P3390）

链接

板，不要忘记取模

T2 斐波那契数列（P1962）

链接

典中典，转移方程的矩阵形式如下：

\[\begin{equation} \begin{gathered} &\begin{bmatrix} f_{i-2} & f_{i-1} \end{bmatrix} & \times &\begin{bmatrix} 0 & 1 \newline 1 & 1 \end{bmatrix} & = &\begin{bmatrix} f_{i-1} & f_{i} \end{bmatrix} \end{gathered} \nonumber \end{equation} \]

上快速幂即可

T3 数学作业（P3216）

链接

不同位数分开处理，做至多 \(18\) 遍矩阵快速幂即可

好像这么说太敷衍了，那么说的细一点——

记 \(f_i = \text{Concatenate}(i)\)，显然有（取模就不写了）

\[f_i = f_{i-1} \times 10^{1 + \lg i} + i \]

首先，答案所代表的矩阵比较显然，形如：

\[\begin{aligned} \begin{bmatrix} f_i & i+1 & 1 \end{bmatrix} \nonumber \end{aligned} \]

然后，我们就先写出来转移式的这一部分

\[\begin{aligned} \begin{gathered} &\begin{bmatrix} f_i & i+1 & 1 \end{bmatrix} & = &\begin{bmatrix} f_{i-1} & i & 1 \end{bmatrix} & \times & P \end{gathered} \nonumber \end{aligned} \]

然后往里填这个方阵 \(P\) 即可，直接把结论放在这里吧！

\[\begin{aligned} \begin{gathered} & P & = \begin{bmatrix} 10^{k} & i & 1 \newline 1 & 1 & 0 \newline 0 & 1 & 1 \end{bmatrix} \end{gathered} \nonumber \end{aligned} \]

然后判断一下临界条件，及时更新 \(P_{1,1}\) 的值

Warning：如果你 WA 最后几个点，请 #define int unsigned long long，原因是最后一次更新会炸

T4 矩阵游戏（P1397）

链接

矩阵的转移写法应该不难，就是这个数据范围有点毒瘤（\(n \le 10^{10^5}\)）

所以是一道十进制快速幂的板题，这个就简单过掉了

T5 生成树计数（P2109）

链接

注：云落还没有通过此题，以下仅展示口胡做法，并不保证正确性

\(k\) 是极小的，并且综合题目无向图的特殊连边性质以及最小生成树的原理（连通块），考虑状压维护连通块

具体地，对于结点 \(u\)，我们只关心 \([u-k+1,u]\) 之间的连通块情况，在转移的时候保证 \([1,u-k]\) 是连通的即可

然后是状压维护连通块，事实上这个不是朴素的考虑某条边是否选入，而是一个类似集合划分的问题

需要说明的是，枚举集合划分的操作在字符串中是我们称之为最小表示法。在计数（组合数学）里，我们说 \(n\) 个数的集合划分的方案数记作 \(\text{Bell}(n)\)，也就是大名鼎鼎的贝尔数
结论：\(\text{Bell}(5) = 52\)

如此小的数量级也给时间复杂度提供了保障

圆规正传，其实状压什么的都出来了，整体就差不多了，但是 \(n\) 的范围总是会给我们带来惊喜

那么大概细化一下——

记 \(f_{i,j}\) 表示考虑到结点 \(i\)，状态为 \(j\) 的方案数，然后预处理一个 \(g_{s,t}\) 表示状态 \(s\) 转移到状态 \(t\) 的贡献

大概方程就是这样的——

\[f_{i,j} \gets \sum_{k} f_{i-1,k} \times g_{k,j} \]

矩阵快速幂直接加速上面这个式子就行

还有一些云落想到的小细节……

• 计算 \(g\) 的时候，对于同一个连通块，不能连入超过 \(1\) 条边，否则就出环了……

• \([1,u-k]\) 要和当前状态的结点中的至少一个点连通……

• 并查集维护不要忘记初始化

T6 Cow Relays G（P2886）

链接

讲故事时间：Once upon a time，云落刷了一个题库叫做高效进阶

这种东西看着就很 Floyd，不过云落确实没有想明白怎么说这个事……

那么直接上正解吧！

设矩阵 \(A\) 表示经过 \(x\) 条边的路径数，矩阵 \(B\) 表示经过 \(y\) 条边的路径数，则 \(A \times B\) 表示经过 \((x+y)\) 条边的路径数，有：

\[C_{i,j} = \sum_{k=1}^{n} (A_{i,k}+B_{k,j}) \]

求路径长度？不是路径数？那有啥区别，把求和号改成 \(\min\) 号不就结了？

\[C_{i,j} = \min_{1 \le k \le n} (A_{i,k}+B_{k,j}) \]

云落愿称之为广义矩阵乘法意义下的矩阵快速幂

T7 【模板】“动态 DP” & 动态树分治（P4719）

链接

素板，速切

T8 保卫王国（P5024）

链接

2018 年，恍如昨日（说人话，就是还热乎着捏！）

结论：最小权覆盖集 \(=\) 全集 \(-\) 最大权独立集

就剩个模板了

后记

打卡下班（最开心的一集）！

完结撒花！