1.14 上午-树上启发式合并 & 线性基
前言
勿让将来,辜负曾经
也许云落是机房里唯一一个不会 DSU-on-tree 的蒟蒻了
正文
知识点
讲了两个算法,或者说是处理一类问题的思路
树上启发式合并(DSU-on-tree)
是一种维护树上信息的离线算法,实现方式比较朴素
简单说一下实现的大致流程:
-
遍历轻儿子,计算它们子树内的答案,但是不向父亲给予贡献(即计算之后直接清空)
-
遍历重儿子,计算答案的同时也向父亲给出贡献(计算之后不请空)
-
再次遍历轻儿子,此时将贡献合并给父亲(维护父亲的答案)
整套流程仍旧是暴力的板式(优雅的暴力),但是时间复杂度是有保障的 \(O(n \log n)\) 的,听上去还不错?
结合例子——
考虑 DSU-on-tree 的实现过程(请注意,DSU-on-tree 需要题目支持离线算法,如果强制在线,建议用树套树等若干强力的数据结构维护!)
首先第一遍 DFS 预处理一些树上的信息(fa,son,sz,dep,dfn,rev……)。很好理解,如果你写过重链剖分,那么这些东西都不在话下
目标:在极优秀的时间复杂度内预处理,并 \(O(1)\) 输出答案
具体地,考查某一个树上的结点 \(u\),对其的答案计算采用启发式合并
- 遍历轻儿子 \(v\),即向下递归计算 \(v\) 子树的答案
for(int v:G[u]){
if(v==fa[u]||v==son[u]){
continue;
}
solve(v,false);
}
- 遍历重儿子 \(son_u\),即向下递归计算 \(son_u\) 的答案
if(son[u]){
solve(son[u],true);
}
- 加入所有儿子的贡献,计算答案
for(int v:G[u]){
if(v==fa[u]||v==son[u]){
continue;
}
for(int i=dfn[v];i<=dfn[v]+sz[v]-1;i++){
ins(rev[i]);
}
}
ins(u);
ans=tol;
- 在加入之前,需要先清除自身贡献,等待第二次计算(轻重儿子可以通过传入布尔型参数来维护)
if(!flag){
for(int i=dfn[u];i<=dfn[u]+sz[u]-1;i++){
del(rev[i]);
}
}
完整代码如下——
点击查看代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int maxn=1e5+5;
int n,m,c[maxn];
vector<int> G[maxn];
int fa[maxn],son[maxn],dep[maxn],sz[maxn];
int dfn[maxn],tim,rev[maxn];
int cnt[maxn],tol,ans[maxn];
inline void dfs(int u,int fath){
fa[u]=fath;
dep[u]=dep[fath]+1;
sz[u]=1;
dfn[u]=++tim;
rev[tim]=u;
int mx=-1;
for(int v:G[u]){
if(v==fath){
continue;
}
dfs(v,u);
sz[u]+=sz[v];
if(sz[v]>mx){
mx=sz[v];
son[u]=v;
}
}
return;
}
inline void ins(int u){
if(!cnt[c[u]]){
tol++;
}
cnt[c[u]]++;
return;
}
inline void del(int u){
cnt[c[u]]--;
if(!cnt[c[u]]){
tol--;
}
return;
}
inline void solve(int u,bool flag){
for(int v:G[u]){
if(v==fa[u]||v==son[u]){
continue;
}
solve(v,false);
}
if(son[u]){
solve(son[u],true);
}
for(int v:G[u]){
if(v==fa[u]||v==son[u]){
continue;
}
for(int i=dfn[v];i<=dfn[v]+sz[v]-1;i++){
ins(rev[i]);
}
}
ins(u);
ans[u]=tol;
if(!flag){
for(int i=dfn[u];i<=dfn[u]+sz[u]-1;i++){
del(rev[i]);
}
}
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n-1;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
for(int i=1;i<=n;i++){
cin>>c[i];
}
dfs(1,0);
solve(1,false);
cin>>m;
for(int i=1;i<=m;i++){
int x;
cin>>x;
cout<<ans[x]<<endl;
}
return 0;
}
众所周知,不说时间复杂度的算法就是耍流氓……所以简单证明一下(挺感性的哈)
先说结论:对于上面这道典题来说,时间复杂度为 \(O(n \log n + m)\)
在证明重链剖分的时间复杂度时,有一条关于重儿子和重链的性质是非常好用的。对于任意一个树上的结点,其返祖链上最多经过 \(\lceil \log n \rceil\) 条轻边
然后观察 DSU-on-tree 的实现过程,我们考查一个节点被遍历到的次数。结论:遍历次数 等于 其返祖链上的轻边条数 \(+1\) (自己本身就需要被遍历到)
为什么嘞?如果它的返祖链上存在一条轻边,那么该子树内它就有前后两次贡献计算;反之,只有一次计算
而轻边数是极有限的 \(O(\log n)\) 量级,所以一个点被遍历到的次数就是 \(O(\log n)\) 量级。树上共计 \(n\) 个结点,所以总时间复杂度为 \(O(n \log n)\)
查询显然是 \(O(m)\) 的哈!
总结:DSU-on-tree 借助离线的思想可以处理一些数据结构不好维护的东西(或者说数据结构可以维护但实现难度大,比如树套树……),并且其时间复杂度比一些暴力的根号算法更优(比如莫队)。应用范围还是挺广泛的哈!代码好写比什么都强——
线性基
线性基是线性代数的一个重要概念。笼统地给出定义——线性基是用一些有限的基向量去描述一些无限的线性空间,这个无限空间我们说它是基向量的张成空间
虽然说的很复杂,但是我们都见过(前置知识:平面向量,空间向量)
对于欧式几何来说(平常见到的就是欧式几何……),平面直角坐标系就是一个张成空间,显然基向量就是我们天天画的坐标轴。换言之,坐标系上每一个点对应的平面向量都可以由相应的 \(x,y\) 的线性组合而成,三维空间也是同理
其实线性基就是在欧式几何上的推广……
线性相关 & 线性无关
基向量(极大线性无关组)之间线性无关——那么什么是线性无关?
简单来说,就是多余
对于某一组基向量的张成空间来说,该空间内任意一个向量都可以由基向量的线性组合表示
举个例子,对于向量 \(\overrightarrow{OC}\),显然有 \(\overrightarrow{OC} = \overrightarrow{OA} + \overrightarrow{OB}\)
对于一个向量组 \(V\),若存在一个向量 \(a_k\) 使得其可以被向量组 \(P\)(满足 \(a_k \notin P \land P \subsetneqq V\))所表示,那么该向量组线性相关
否则,该向量组线性无关
那么对于一个给定的向量组,我们可以通过消去一些“多余的”向量,使得剩余的向量组线性无关。我们称这个向量组叫做极大线性无关组,其中每一个向量叫做基向量
说人话就是,由基向量构成的极大线性无关组是最少的可以将给定的向量组通过线性组合表述出来的
接下来把云落刚才写的全部忘掉,我们要短暂地告别线性代数,回归 oi 咯!
在 oi 中,线性基特指异或线性基,是用于解决一些与异或有关的问题,包括但不限于:
-
判断一个数能否表示成某数集子集的异或和
-
求一个数表示成某数集子集异或和的方案数
-
求某数集子集的最大/最小/第 k 大/第 k 小异或和
-
求一个数在某数集子集异或和中的排名
线性基本身挺黑盒的,因为它属于一种构造型的算法。一些和线性基有关的题目都绕不开构造线性基
先插一句,线性基的重要性质(其实前面都写了,但是回归 oi 之后还是复述一下比较好)
-
原序列的任意一个数都可以由线性基内部的一些数异或得到
-
线性基内部的任意数异或起来都不能得到 \(0\)
-
线性基内部的数个数唯一且是所有满足性质一的构造方案中个数最少的
构造序列的异或线性基一般有两种做法:贪心或高斯消元
贪心做法是在线的,考虑每次将一个元素插入序列并构造线性基
具体地,我们先对原序列做一步转二进制,然后从高位到低位枚举。对于待插入的一个数 \(x\) 如果之前构造的线性基 \(P\) 中不存在这一位为 \(1\) 的基向量 \(P_i\),那么直接就将当前的数插入线性基;否则,令 \(x \gets x \oplus P_i\)
这个贪心是有正确性的,读者自证不难
如果各位接触过高斯消元解异或方程组,那么这玩意就是一眼秒;如果没接触过,先去高斯消元那里接触接触
一题一解
T1 Race(P4191)
居然评了紫题(甚至这还是 IOI 的题目……)
P.S. 正解是点分治,但是为什么不写简单无脑地 DSU-on-tree 捏?
还是考虑 DSU-on-tree,那么我们需要去观察什么东西可能会给答案造成贡献,显然是距离恰好为 \(k\) 的点对。形式化地,我们记 \(\text{dis}(x,y)\) 表示路径长度(即路径上的边权和),对于所有 \(\text{dis}(x,y) = k\) 的点对 \((x,y)\),都会给答案造成贡献
特别地,如果不存在这样的点对 \((x,y)\),自然是题目中所描述的无解的情况
接下来我们要细化一些这个贡献到底是什么。是路径 \((x,y)\) 所经过的边数。为了方便表述,记 \(\text{dep}_x\) 表示 \(x\) 结点的深度。考虑路径问题,不难想到 LCA 与树上差分,所以这个贡献显然是
类似地,刚才对于贡献的判定条件也可以写成
那么索性,我们不记录 \(\text{dis}(x,y)\),直接记录 \(\text{dis}_x\) 表示 \(\text{dis}(1,x)\) 即可。判定式子就可以改写成
回到 DSU-on-tree 上来,我们发现对于 \(u\) 子树的贡献来源可以有三部分组成:一种是 \(lca = u\) 的,另一种是 \(lca\) 在 \(v\) 的子树中
后者可以递归向下转化为前者,考虑怎么统计 \(lca=u/v\) 的贡献
注意到这个实现过程和 DSU-on-tree 的过程很类似,先统计 \(lca\) 在 \(v\) 子树内的贡献,再向上合并给 \(lca=u\) 的情况
观察这个判定式子——
假设我们枚举的结点为 \(v\),那么我们现在已知的是 \(dis_y\)(也就是当前枚举的 \(v\)),\(dis_{lca}\)(众所周知,\(lca=u\)),以及 \(k\)(这是输入得到的),所以把未知的 \(\text{dis}_x\) 拉到一遍,移项得
需要查询这个东西在之前的枚举中是否出现过,用 map 维护即可
当然,有一个小细节,如果这条路径是一个返祖关系,也要计算进去
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e5+5,inf=9e18;
int n,k;
int head[maxn],tot;
struct Edge{
int to,nxt,val;
}e[maxn<<1];
int fa[maxn],son[maxn],dep[maxn],dis[maxn],sz[maxn];
int dfn[maxn],tim,rev[maxn];
map<int,int> mp;
int ans=inf;
inline void add(int u,int v,int w){
e[++tot].to=v;
e[tot].val=w;
e[tot].nxt=head[u];
head[u]=tot;
return;
}
inline void dfs(int u,int fath){
fa[u]=fath;
dep[u]=dep[fath]+1;
sz[u]=1;
dfn[u]=++tim;
rev[tim]=u;
int mx=-1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to,w=e[i].val;
if(v==fath){
continue;
}
dis[v]=dis[u]+w;
dfs(v,u);
sz[u]+=sz[v];
if(sz[v]>mx){
mx=sz[v];
son[u]=v;
}
}
return;
}
inline void ins(int u){
if(!mp[dis[u]]){
mp[dis[u]]=dep[u];
}else{
mp[dis[u]]=min(mp[dis[u]],dep[u]);
}
return;
}
inline void solve(int u,bool flag){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa[u]||v==son[u]){
continue;
}
solve(v,false);
}
if(son[u]){
solve(son[u],true);
}
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa[u]||v==son[u]){
continue;
}
for(int j=dfn[v];j<=dfn[v]+sz[v]-1;j++){
int len=k+dis[u]*2-dis[rev[j]];
if(mp[len]){
ans=min(ans,dep[rev[j]]+mp[len]-dep[u]*2);
}
}
for(int j=dfn[v];j<=dfn[v]+sz[v]-1;j++){
ins(rev[j]);
}
}
ins(u);
if(mp[dis[u]+k]){
ans=min(ans,mp[dis[u]+k]-dep[u]);
}
if(!flag){
mp.clear();
}
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>k;
for(int i=1;i<=n-1;i++){
int u,v,w;
cin>>u>>v>>w;
u++;
v++;
add(u,v,w);
add(v,u,w);
}
dfs(1,0);
solve(1,false);
if(ans==inf){
cout<<-1<<endl;
return 0;
}
cout<<ans<<endl;
return 0;
}
T2 天天爱跑步(P1600)
被各种做法打烂的题目(树剖,LCT,DSU-on-tree,树上差分,线段树合并,扫描线……)
不同做法 \(++\)
静态树上信息维护(直接想线段树合并……),并且支持离线,考虑 DSU-on-tree
需要形式化贡献的计算方式,我们发现当 \(\text{dep},\text{w}\) 之间满足某种关系的时候,会给答案造成贡献
考虑每次询问 \((s,t)\),注意到一次跑步任务会按照 LCA 拆分成两段,形如:
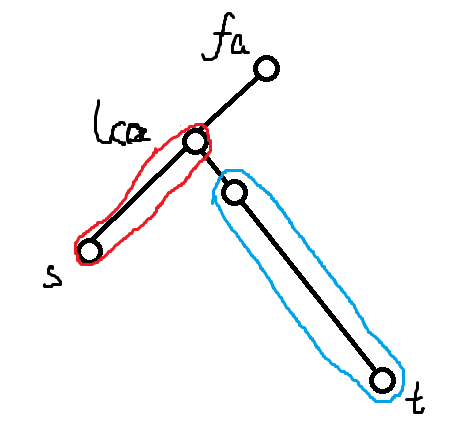
对于红色的上行部分,若一个结点 \(i\) 有贡献,当且仅当
同理,对于蓝色的下行部分,结点 \(i\) 有贡献当且仅当
将上述式子整理移项,有
上行:
下行:
做到这里基本上就和上一道题很类似咯,只不过需要针对上下行维护两个桶数组(当然云落是用 map 实现的),计算贡献略复杂一些,贴个代码自行理解即可
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=3e5+5;
int n,m,w[maxn];
vector<int> G[maxn];
int fa[maxn],son[maxn],dep[maxn],sz[maxn];
int dfn[maxn],tim,Top[maxn],rev[maxn];
vector<int> d[maxn][4];
map<int,int> up,down;
int ans[maxn];
inline void dfs1(int u,int fath){
fa[u]=fath;
dep[u]=dep[fath]+1;
sz[u]=1;
int mx=-1;
for(int v:G[u]){
if(v==fath){
continue;
}
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>mx){
mx=sz[v];
son[u]=v;
}
}
return;
}
inline void dfs2(int u,int tp){
dfn[u]=++tim;
Top[u]=tp;
rev[tim]=u;
if(!son[u]){
return;
}
dfs2(son[u],tp);
for(int v:G[u]){
if(v==fa[u]||v==son[u]){
continue;
}
dfs2(v,v);
}
return;
}
inline int LCA(int x,int y){
while(Top[x]!=Top[y]){
if(dep[Top[x]]<dep[Top[y]]){
swap(x,y);
}
x=fa[Top[x]];
}
return dep[x]<=dep[y]?x:y;
}
inline void add(int u,int wson){
for(int i:d[u][0]){
up[i]++;
}
for(int i:d[u][1]){
up[i]--;
}
for(int i:d[u][2]){
down[i]++;
}
for(int i:d[u][3]){
down[i]--;
}
for(int v:G[u]){
if(v==fa[u]||v==wson){
continue;
}
add(v,wson);
}
return;
}
inline void solve(int u,bool flag){
for(int v:G[u]){
if(v==fa[u]||v==son[u]){
continue;
}
solve(v,false);
}
if(son[u]){
solve(son[u],true);
}
add(u,son[u]);
ans[u]=up[dep[u]+w[u]]+down[w[u]-dep[u]];
if(!flag){
up.clear();
down.clear();
}
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n-1;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
for(int i=1;i<=n;i++){
cin>>w[i];
}
dfs1(1,0);
dfs2(1,1);
for(int i=1;i<=m;i++){
int s,t;
cin>>s>>t;
int lca=LCA(s,t);
d[s][0].push_back(dep[s]);
d[fa[lca]][1].push_back(dep[s]);
d[t][2].push_back(dep[s]-2*dep[lca]);
d[lca][3].push_back(dep[s]-2*dep[lca]);
}
solve(1,false);
for(int i=1;i<=n;i++){
cout<<ans[i]<<' ';
}
return 0;
}
不推荐参考云落的写法哈!是这样的,DSU-on-tree 用到了重儿子等信息,正好还要求 LCA,所以索性云落就敲了一个树链剖分上去,然后对于计算贡献的部分云落单写了一个函数,用于维护子树问题
比较难参悟透彻的应当是代码中 vector d[maxn][4] 数组的含义。其实就是一个典型的树上差分,以上行为例,可以感性理解为给这段路径每个点发放了一个 \(dep_s\) 的物品。但是这个发放物品的过程不支持暴力发放,所以写了一个差分进去,大家自行理解哈!
T3 【模板】线性基(P3812)
板,构造线性基 \(p\) 后由高位至低位取 \(\max (res,res \oplus p_i)\) 即可
嗯呐——不开祖宗见 long long
点击查看代码
#include<iostream>
#define int long long
using namespace std;
const int M=64;
int n,p[M];
inline void ins(int x){
for(int i=M-1;i>=0;i--){
if(x&(1ll<<i)){
if(p[i]==0){
p[i]=x;
return;
}
x^=p[i];
}
}
return;
}
inline int query(){
int res=0ll;
for(int i=M-1;i>=0;i--){
res=max(res,res^p[i]);
}
return res;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
int x;
cin>>x;
ins(x);
}
int ans=query();
cout<<ans<<endl;
return 0;
}
T4 元素(P4570)
两句话题意:一个长度为 \(n\) 的序列,序列上的每个元素都具有两个属性——编号、权值。现在要在序列中选出一部分元素,使得在满足这些元素编号的线性无关性之后权值最大
其实就是一个简单的贪心结论,按权值非严格递减排序,然后一次插入线性基即可
做一些比较感性的贪心结论证明
一些性质
-
极大线性无关组的集合大小(也就是基向量的个数)是固定的
-
异或的逆运算仍然是异或
简单举一个实例,若在一个向量组中出现了如下情况
若仅考虑维护其线性无关性,“剔除” \(a,b,c\) 三个向量实际上是等价的
说到这里基本上就完结了,我们为了让权值最大,所以每次剔除总选择权值最小的剔除。换言之,在插入线性基之前,肯定优选权值大的元素
证明完贪心,代码是好实现的,简单排序然后构造线性基即可
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1024,M=64;
int n;
struct node{
int x,y;
bool operator < (node s){
return y>s.y;
}
}a[maxn];
int p[M],ans;
inline bool ins(int x){
for(int i=M-1;i>=0;i--){
if(x&(1ll<<i)){
if(p[i]==0){
p[i]=x;
return true;
}
x^=p[i];
}
}
return false;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
int pos,val;
cin>>pos>>val;
a[i]={pos,val};
}
sort(a+1,a+n+1);
for(int i=1;i<=n;i++){
bool flag=ins(a[i].x);
if(flag){
ans+=a[i].y;
}
}
cout<<ans<<endl;
return 0;
}
T5 最大 XOR 和路径(P4151)
一句话题意:给定一个带边权的无向连通图,求 \(1\) 到 \(N\) 的一条路径使得该路径在所有 \(1\) 到 \(N\) 的方案中,边权的异或和最大,输出这个最大的异或和
其实题干提示了我们,重复经过的边,边权要重复计算。而异或的性质非常好,有 \(x \oplus x = 0\)
考虑如何利用这个性质,不妨先完成一个弱化版——钦定这个无向连通图是一棵树
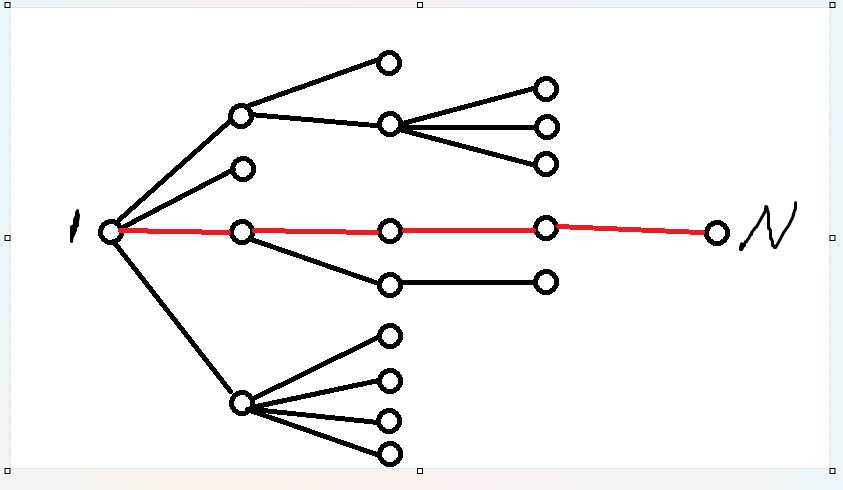
简单手模一下,发现答案是唯一的,即所有红色边边权的异或和
因为对于树上的路径是唯一的,所以如果走黑色边,一定会一去一返,经过偶数次。而对于异或运算来说偶数次异或同一个数是没有任何贡献滴!
那么,在原问题中可以把具有树性质的结构给略去,换言之,仅考虑环的影响
继续考虑一个弱化版
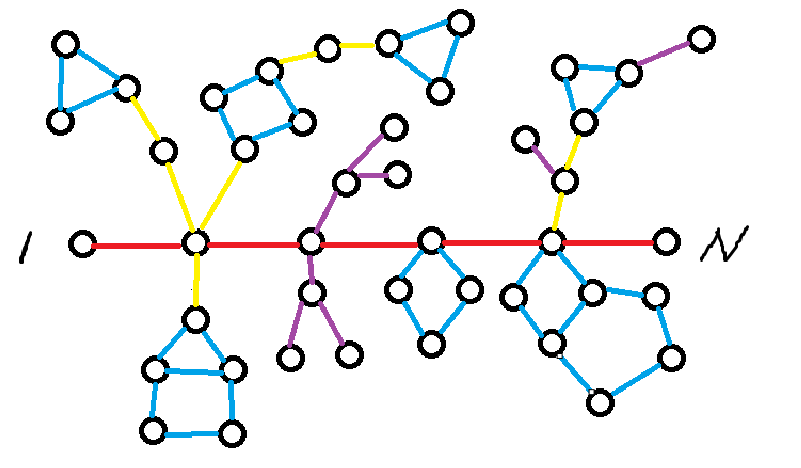
别看这个图长的很复杂,但实际上简单分析一下就可以了
紫色边就是类似树形结构的东西,可以扔掉不管,然后这里就只剩下两种结构,分类讨论一下即可
- 链带环
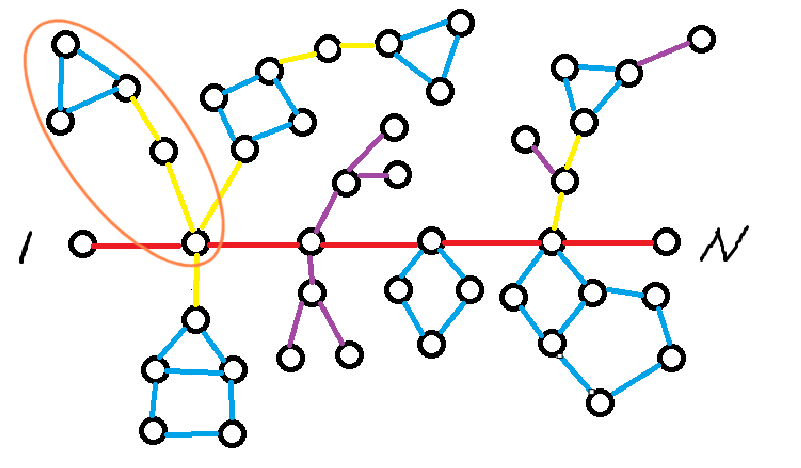
橙色椭圆圈出来的部分就很神奇,我们发现如果走入这条支路,我们不再是获得 \(0\) 的贡献,而是可以获得蓝色边的贡献,也就是环的贡献。黄色边是桥,所以一定被走两次,不造成贡献
- 环套环
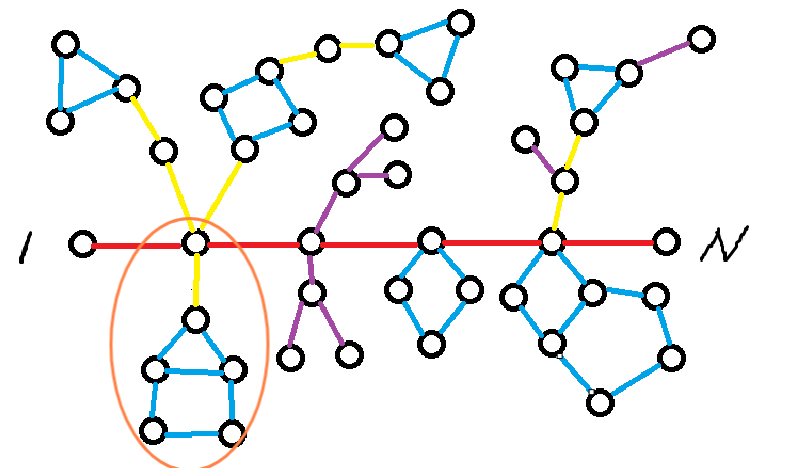
自己手模吧,结论还是造成环的贡献(请注意是环的贡献,而不是环的边集的并集造成贡献)。对应到原图的例子上,就是可能只有靠上的三元环给贡献,可能只有靠下的四元环给贡献,还可能是外面的五元环给贡献
- 挂环
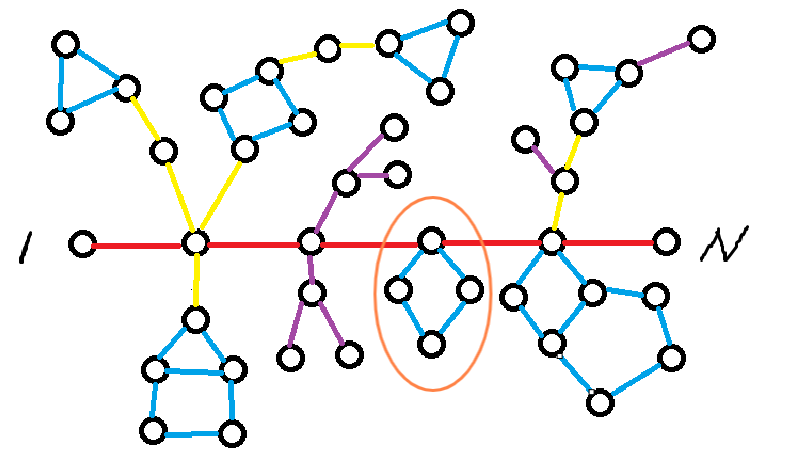
不论是链挂环还是环挂环,本质上和链带环没有任何差异
也就是说对于这个稍强一些的弱化版,结论就是求环与红色路径的最大异或和
接下来考虑原问题,很多人可能不理解上面东西到底哪里弱化了,其实忽略掉了一种情况,我们来再看一个图
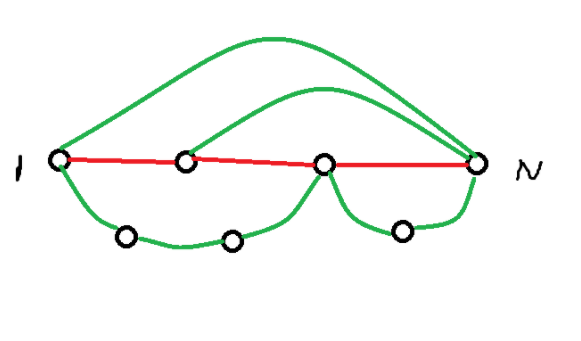
云落称之为链粘环,其实你发现,这种情况等价于 $1 \to N $ 存在多条简单路径。注意到刚才的结论是仍然适用的,直接把环拎出来,随便找一条简单路径,求最大异或和即可
综上所述,原问题转化为了两个子问题
-
找环
-
求最大异或和
直接做做完了,代码难度不大,这道题目还是挺偏思维的
点击查看代码
#include<iostream>
#define int long long
using namespace std;
const int maxn=5e4+10,maxm=1e5+10,M=64;
int n,m;
int head[maxn],tot;
struct Edge{
int to,nxt,val;
}e[maxm<<1];
int dis[maxn];
bool vis[maxn];
int p[M];
inline void add(int u,int v,int w){
e[++tot].to=v;
e[tot].val=w;
e[tot].nxt=head[u];
head[u]=tot;
return;
}
inline void ins(int x){
for(int i=M-1;i>=0;i--){
if(x&(1ll<<i)){
if(p[i]==0){
p[i]=x;
return;
}
x^=p[i];
}
}
return;
}
inline void dfs(int u,int d){
dis[u]=d;
vis[u]=true;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to,w=e[i].val;
if(vis[v]){
ins(d^w^dis[v]);
continue;
}
dfs(v,d^w);
}
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
add(u,v,w);
add(v,u,w);
}
dfs(1,0);
int ans=dis[n];
for(int i=M-1;i>=0;i--){
ans=max(ans,ans^p[i]);
}
cout<<ans<<endl;
return 0;
}
T6 albus 就是要第一个出场(P4869)
科普题 or 小清新结论题
结论:对于这个异或出来的数,每个数都出现恰 \(2^{n-|V|}\) 次,其中 \(n\) 是序列长度,\(|V|\) 是线性基大小
先不提这个结论的证明,简单说一下计算答案的方式。
可以直接记录每个有值的位置 \(pos\) 及线性基中比它小的位置上有值的位置个数 \(cnt\),枚举每个满足 \(k\) 在二进制第 \(pos\) 位有值的位置作为最高的不选位置,剩下更低位随便选,方案数 \(2^{cnt}\),简单累加一下即可
然后就是比较抽象的证明……
注意到线性“基”,也就是说原来的所有数都可以被基向量的线性组合表示。那么我们随机选一个不在线性基中的数 \(x\),自然地,它可以被线性基表示出来
形式化地,有 \(a_{k_1} \oplus ... \oplus a_{k_p} = x\)(应该好理解吧),移项有 \(a_{k_1} \oplus ... \oplus a_{k_{p-1}} \oplus x = a_{k_p}\)
上面这个鬼东西有个推论,注意力惊人的云落发现,在线性基中的任何一个数都可以用类似方式表示出来,并且这个东西只和 \(x\) 的选取方案有关(因为线性基中总能找到一个方案与 \(x\) 的选取方案对应)
而不在线性基的数一共有 \(n-|V|\),每个数都有选或不选两种方案,所以对于一个数的出现次数,答案的下界是 \(2^{n-|V|}\)
上界也是 \(2^{n-|V|}\),因为线性基的选取方案是唯一的(其实的“总能找到一个方案与之对应”应该描述为“总能找到有且仅有一个方案与之对应”)
证毕,撒花!
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int M=64,mod=10086;
int n,q;
int p[M],pos,cnt;
inline int qpow(int a,int b){
int res=1;
while(b){
if(b&1){
res=res*a%mod;
}
a=a*a%mod;
b>>=1;
}
return res;
}
inline void ins(int x){
for(int i=M-1;i>=0;i--){
if(x&(1ll<<i)){
if(p[i]==0){
p[i]=x;
return;
}
x^=p[i];
}
}
return;
}
inline void kth(int k){
for(int i=0;i<=M-1;i++){
if(p[i]==0){
continue;
}
if(k&(1ll<<i)){
pos+=(1ll<<cnt);
}
cnt++;
}
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
int x;
cin>>x;
ins(x);
}
cin>>q;
kth(q);
cout<<pos*qpow(2,n-cnt)%mod+1;
return 0;
}
T7 无力回天(P11620)
前言:这道题目 luogu 更了一下题号,所以会 WA,去上面的传送门交吧!
一句话题意:用数据结构维护区间异或以及求区间最大异或和的操作
其实思路并不难,就是 Ynoi 的题目都是一些毒瘤数据结构题(然而这个题目一点也不毒瘤),debug 难度很大
先考虑一个弱化版——单点异或,区间最大异或和(可以参考这道题目,云落的参考代码放这里咯)
简单说一下这道弱化版的做法,就是线段树维护线性基。什么意思捏,我们线段树的每一个区间不再维护什么区间和,区间最值,而是直接把这个区间的线性基扔进去
比较好想的是 modify 和 query。单点修改操作可以理解为,给这个结点对应的线性基插入一个数。query 就是找到相应的区间分拆方案,把所有的线性基合并到一块去,最后再做求最大异或和的工作
其实说到这里,难想的 pushup 操作就呼之欲出了,也就是两个小区间的线性基的合并
因为线性基的个数是极少的,所以整个合并过程的时间复杂度是有保障的
然后就比较简单咯,区间修改转化为单点修改的经典 trick 就是树状数组维护差分数组捏,然后再把刚刚上面的代码修修补补即可
点击查看代码
#include<iostream>
#include<cstring>
#define endl '\n'
using namespace std;
const int maxn=5e4+5,M=32;
int n,m,a[maxn];
struct Linear_basis{
int p[M];
void clr(){
memset(p,0,sizeof(p));
return;
}
void ins(int x){
for(int i=M-1;i>=0;i--){
if(x&(1ll<<i)){
if(p[i]==0){
p[i]=x;
return;
}
x^=p[i];
}
}
return;
}
void merge(Linear_basis x){
for(int i=M-1;i>=0;i--){
if(x.p[i]){
ins(x.p[i]);
}
}
return;
}
int solve(int x){
int res=x;
for(int i=M-1;i>=0;i--){
res=max(res,res^p[i]);
}
return res;
}
};
struct Segment_tree{
struct node{
int l,r;
Linear_basis lb;
}tr[maxn<<2];
void pushup(int u){
tr[u].lb.clr();
tr[u].lb.merge(tr[u<<1].lb);
tr[u].lb.merge(tr[u<<1|1].lb);
return;
}
void build(int u,int l,int r){
tr[u].l=l;
tr[u].r=r;
tr[u].lb.clr();
if(l==r){
tr[u].lb.ins(a[l]);
return;
}
int mid=l+r>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
return;
}
void modify(int u,int pos,int k){
int l=tr[u].l,r=tr[u].r;
if(l==pos&&r==pos){
tr[u].lb.clr();
tr[u].lb.ins(a[pos]^=k);
return;
}
int mid=l+r>>1;
if(pos<=mid){
modify(u<<1,pos,k);
}else{
modify(u<<1|1,pos,k);
}
pushup(u);
return;
}
Linear_basis query(int u,int ql,int qr){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r){
return tr[u].lb;
}
int mid=l+r>>1;
Linear_basis res;
res.clr();
if(ql<=mid){
res.merge(query(u<<1,ql,qr));
}
if(qr>mid){
res.merge(query(u<<1|1,ql,qr));
}
return res;
}
}Tr;
struct BIT{
int c[maxn];
int lowbit(int x){
return x&(-x);
}
void add(int x,int k){
while(x<=n){
c[x]^=k;
x+=lowbit(x);
}
return;
}
int ask(int x){
int res=0;
while(x){
res^=c[x];
x-=lowbit(x);
}
return res;
}
}bit;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=n-1;i>=1;i--){
a[i+1]^=a[i];
}
for(int i=1;i<=n;i++){
bit.add(i,a[i]);
}
Tr.build(1,1,n);
while(m--){
int opt,l,r,v;
cin>>opt>>l>>r>>v;
if(opt==1){
bit.add(l,v);
Tr.modify(1,l,v);
if(r<=n-1){
bit.add(r+1,v);
Tr.modify(1,r+1,v);
}
}else{
int tmp=bit.ask(l);
if(l==r){
cout<<max(tmp^v,v)<<endl;
continue;
}
Linear_basis ans=Tr.query(1,l+1,r);
ans.ins(tmp);
cout<<ans.solve(v)<<endl;
}
}
return 0;
}
后记
最简单的一集
完结撒花!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号