1.13 上午-树链剖分
前言
我累个超绝 debug 难度啊!
勿让将来,辜负曾经
正文
知识点
树链剖分其实是一类算法的合称,如果只说树链剖分,我们认为是指重链剖分。抛却重链剖分,树链剖分还包含长链剖分(用于优化 DP),实链剖分(用于 LCT)
显然这节课是重链剖分的一次专题强化课捏!
树链剖分的核心思想是通过维护“重链”解决树上问题,理解重链建议结合图示哈!
云落盗张图——
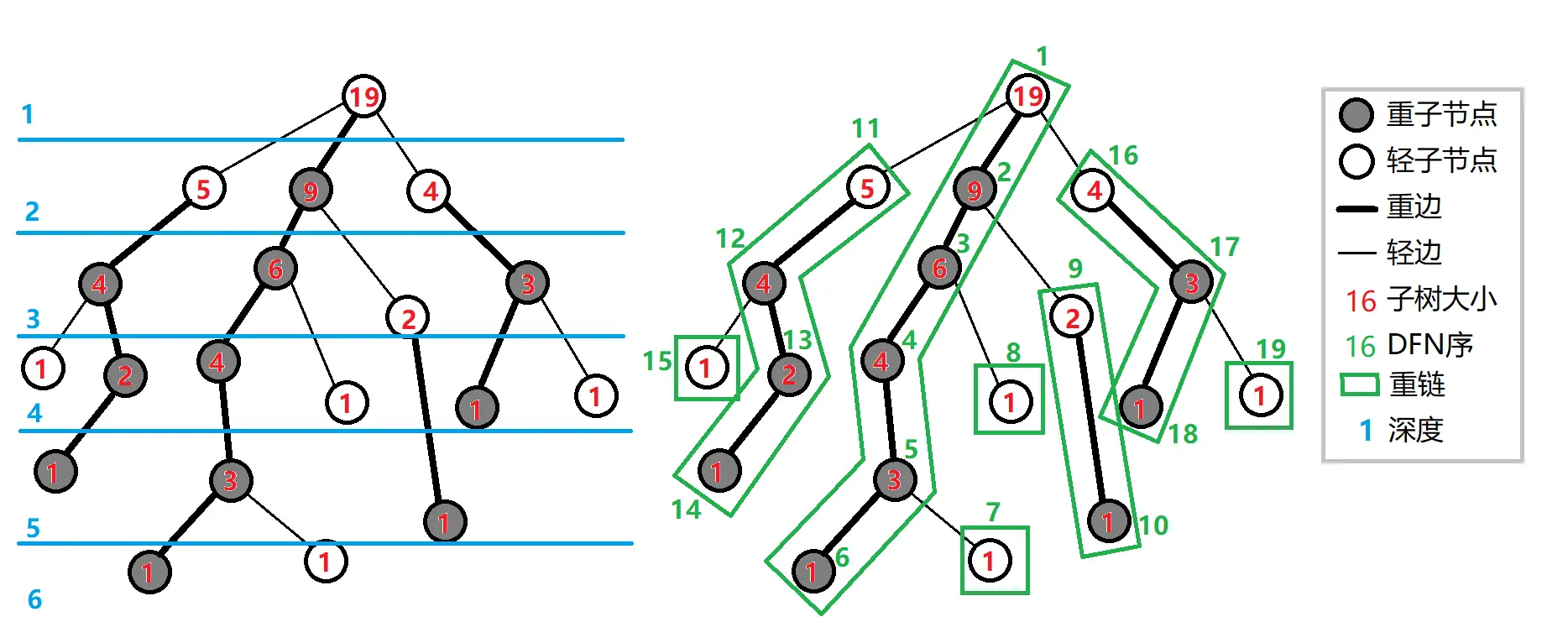
重链剖分可用于维护 LCA,也可结合线段树维护链信息,子树信息等
安利一篇云落的早期博客,可能写得很抽象捏
一题一解
T1 【模板】重链剖分/树链剖分(P3384)
模板题,不想多说,浅聊两句。
某一场模拟赛,云落顺利地 15 min 瞪出正解,是一个需要重链剖分维护的 DP。没有被 T1 降智的云落非常开心,然后那天就开心了这么一会……原因是,一个简单的树链剖分整场模拟赛云落都没有调出来,反复地重构确实让云落有点麻木了。现在想起来还是有点后怕,后来刷了一些树链剖分的题目,但是嘛——效果不佳。只能说树链剖分是一个熟能生巧的东西, 唉——((ε=(´ο`*)))。
这警示我们,模拟赛的时候不要死磕一道题(虽然那场模拟赛的其它题目云落一道也不会 qwq),并且功夫要下在平时。云落自认为给树链剖分这个算法分配的时间还算不少,板子也是敲了不下十遍咯,但是嘛,哑巴吃黄连哟……
不建议各位对着题解或者对着模板写树链剖分,建议充分理解后自己独立完成树链剖分模板题哈!
多唠叨一句,前几日云落的队友就链式前向星和 vector 实现邻接表存图哪个更优大干了一架。作为两种方法混用的云落瑟瑟发抖,如果屏幕前的你有食用树形 DP 题解中的代码的话,你会注意到云落两种方法都会用到。
事实上是这样的,云落倒不是真的随心所欲哈,还是有一些学问在里面。
链式前向星时空常数均略优于 vector 实现邻接表,但是这点小常数完全可以忽略不计。
云落想说的是,在面对一些复杂图论的情况下,具体地,存在边权,网络流等题目的时候,推荐使用链式前向星。毕竟一个结构体写的会很清楚,调用起来也很好看(而且云落不太了解网络流的 vector 写法,据说很复杂)。
这时候有人肯定会抬杠,vector 也可以套用结构体!你猜云落为什么要先说时空常数?当 vector 等其它 STL 套用非整型结构的时候,慢的离谱。
举两个实例哈,还是刚才那一场模拟赛,云落的一个很厉害的学长,写了一个 vector 套结构体,TLE 了 \(12\) 个点,和打暴力一个分数,改成链式前向星后抢到了时间最优解,就很离谱……另外一个栗子,云落和火腿肠在某一场模拟赛挂了 \(40pts\),原因是使用了平衡树的结构(其实是一个二分套二维数点问题),然后直接 T 飞了。云落用的 map<double,int> 离散化 + 树状数组维护,火腿肠手搓了一颗 FHQ_Treap,然后就双双起飞
但是如果说,一条边就只有孤零零的两个端点 \(u,v\),这时候云落就很喜欢用 vector 实现邻接表。不为别的,就为了好写。一部分原因是云落的码风比较冗长,所以能节省一些代码自然是节省一些比较好哇!
不多说了哈,有点跑题了,贴个模板代码跑路咯!
点击查看代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int maxn=1e5+10;
int n,m,rt,p,a[maxn];
vector<int> G[maxn];
int fa[maxn],son[maxn],dep[maxn],sz[maxn];
int dfn[maxn],tim,Top[maxn],rev[maxn];
struct Segment_tree{
struct node{
int l,r,sum,tag;
}tr[maxn<<2];
void pushup(int u){
tr[u].sum=(tr[u<<1].sum+tr[u<<1|1].sum)%p;
return;
}
void pushdown(int u){
if(tr[u].tag==0){
return;
}
int k=tr[u].tag;
tr[u<<1].sum=(tr[u<<1].sum+k*(tr[u<<1].r-tr[u<<1].l+1)%p)%p;
tr[u<<1|1].sum=(tr[u<<1|1].sum+k*(tr[u<<1|1].r-tr[u<<1|1].l+1)%p)%p;
tr[u<<1].tag=(tr[u<<1].tag+k)%p;
tr[u<<1|1].tag=(tr[u<<1|1].tag+k)%p;
tr[u].tag=0;
return;
}
void build(int u,int l,int r){
tr[u].l=l;
tr[u].r=r;
if(l==r){
tr[u].sum=rev[l]%p;
return;
}
int mid=l+r>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
return;
}
void modify(int u,int ql,int qr,int k){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r){
tr[u].sum=(tr[u].sum+k*(r-l+1)%p)%p;
tr[u].tag=(tr[u].tag+k)%p;
return;
}
pushdown(u);
int mid=l+r>>1;
if(ql<=mid){
modify(u<<1,ql,qr,k);
}
if(qr>mid){
modify(u<<1|1,ql,qr,k);
}
pushup(u);
return;
}
int query(int u,int ql,int qr){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r){
return tr[u].sum%p;
}
pushdown(u);
int mid=l+r>>1,res=0;
if(ql<=mid){
res=(res+query(u<<1,ql,qr))%p;
}
if(qr>mid){
res=(res+query(u<<1|1,ql,qr))%p;
}
return res%p;
}
}Tr;
inline void dfs1(int u,int fath){
fa[u]=fath;
dep[u]=dep[fath]+1;
sz[u]=1;
int mx=-1;
for(int v:G[u]){
if(v==fath){
continue;
}
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>mx){
mx=sz[v];
son[u]=v;
}
}
return;
}
inline void dfs2(int u,int tp){
dfn[u]=++tim;
Top[u]=tp;
rev[tim]=a[u];
if(!son[u]){
return;
}
dfs2(son[u],tp);
for(int v:G[u]){
if(v==fa[u]||v==son[u]){
continue;
}
dfs2(v,v);
}
return;
}
inline void update_chain(int u,int v,int w){
w%=p;
while(Top[u]!=Top[v]){
if(dep[Top[u]]<dep[Top[v]]){
swap(u,v);
}
Tr.modify(1,dfn[Top[u]],dfn[u],w);
u=fa[Top[u]];
}
if(dep[u]>dep[v]){
swap(u,v);
}
Tr.modify(1,dfn[u],dfn[v],w);
return;
}
inline int query_chain(int u,int v){
int res=0;
while(Top[u]!=Top[v]){
if(dep[Top[u]]<dep[Top[v]]){
swap(u,v);
}
res=(res+Tr.query(1,dfn[Top[u]],dfn[u]))%p;
u=fa[Top[u]];
}
if(dep[u]>dep[v]){
swap(u,v);
}
res=(res+Tr.query(1,dfn[u],dfn[v]))%p;
return res;
}
inline void update_subtree(int u,int k){
k%=p;
Tr.modify(1,dfn[u],dfn[u]+sz[u]-1,k);
return;
}
inline int query_subtree(int u){
int res=Tr.query(1,dfn[u],dfn[u]+sz[u]-1)%p;
return res;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m>>rt>>p;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n-1;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs1(rt,0);
dfs2(rt,rt);
Tr.build(1,1,n);
for(int k=1;k<=m;k++){
int opt;
cin>>opt;
if(opt==1){
int x,y,z;
cin>>x>>y>>z;
update_chain(x,y,z);
}else if(opt==2){
int x,y;
cin>>x>>y;
int ans=query_chain(x,y)%p;
cout<<ans<<endl;
}else if(opt==3){
int x,z;
cin>>x>>z;
update_subtree(x,z);
}else if(opt==4){
int x;
cin>>x;
int ans=query_subtree(x)%p;
cout<<ans<<endl;
}
}
return 0;
}
T2 软件包管理器(P2416)
一句话题意:树上维护三个操作,路径修改,子树修改,全局和
上面那个板子稍微改改就好了哇!
一些细节:
-
编号从 \(0\) 开始
-
tag不建议初始化为 \(0\),存在赋值为 \(0\) 的操作 -
如果你是直接把板子贴过来的,主函数的部分请留心
-
虽然这道题目并不需要用到重编号,但是还是写一下形成习惯比较好
-
pushdown最后给tag恢复初值的时候别写挂了
点击查看代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int maxn=2e5+10;
int n,q;
vector<int> G[maxn];
int fa[maxn],son[maxn],dep[maxn],sz[maxn];
int dfn[maxn],tim,Top[maxn],rev[maxn];
struct Segment_tree{
struct node{
int l,r,sum,tag;
}tr[maxn<<2];
void pushup(int u){
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
return;
}
void pushdown(int u){
if(tr[u].tag==-1){
return;
}
int k=tr[u].tag;
tr[u<<1].sum=k*(tr[u<<1].r-tr[u<<1].l+1);
tr[u<<1|1].sum=k*(tr[u<<1|1].r-tr[u<<1|1].l+1);
tr[u<<1].tag=k;
tr[u<<1|1].tag=k;
tr[u].tag=-1;
return;
}
void build(int u,int l,int r){
tr[u].l=l;
tr[u].r=r;
tr[u].tag=-1;
if(l==r){
return;
}
int mid=l+r>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
return;
}
void modify(int u,int ql,int qr,int k){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r){
tr[u].sum=k*(r-l+1);
tr[u].tag=k;
return;
}
pushdown(u);
int mid=l+r>>1;
if(ql<=mid){
modify(u<<1,ql,qr,k);
}
if(qr>mid){
modify(u<<1|1,ql,qr,k);
}
pushup(u);
return;
}
int query(int u,int ql,int qr){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r){
return tr[u].sum;
}
pushdown(u);
int mid=l+r>>1,res=0;
if(ql<=mid){
res+=query(u<<1,ql,qr);
}
if(qr>mid){
res+=query(u<<1|1,ql,qr);
}
return res;
}
}Tr;
inline void dfs1(int u,int fath){
fa[u]=fath;
dep[u]=dep[fath]+1;
sz[u]=1;
int mx=-1;
for(int v:G[u]){
if(v==fath){
continue;
}
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>mx){
mx=sz[v];
son[u]=v;
}
}
return;
}
inline void dfs2(int u,int tp){
dfn[u]=++tim;
Top[u]=tp;
rev[tim]=u;
if(son[u]==0){
return;
}
dfs2(son[u],tp);
for(int v:G[u]){
if(v==fa[u]||v==son[u]){
continue;
}
dfs2(v,v);
}
return;
}
inline void update(int u,int v,int k){
while(Top[u]!=Top[v]){
if(dep[Top[u]]<dep[Top[v]]){
swap(u,v);
}
Tr.modify(1,dfn[Top[u]],dfn[u],k);
u=fa[Top[u]];
}
if(dep[u]>dep[v]){
swap(u,v);
}
Tr.modify(1,dfn[u],dfn[v],k);
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=2;i<=n;i++){
int x;
cin>>x;
G[++x].push_back(i);
}
dfs1(1,0);
dfs2(1,1);
Tr.build(1,1,n);
cin>>q;
while(q--){
string s;
int x;
cin>>s>>x;
x++;
int pre=Tr.tr[1].sum;
if(s[0]=='i'){
update(1,x,1);
int cur=Tr.tr[1].sum;
cout<<abs(cur-pre)<<endl;
}else{
Tr.modify(1,dfn[x],dfn[x]+sz[x]-1,0);
int cur=Tr.tr[1].sum;
cout<<abs(cur-pre)<<endl;
}
}
return 0;
}
T3 旅行(P3313)
山东省选是这样的……
首先,一眼树链剖分,维护路径修改,路径和与路径最大值
如果诸位对 P4556 雨天的尾巴 /【模板】线段树合并 还有印象的话,可能更容易想到这道题目的正解
倒不是说这道题要用什么线段树合并去维护,而是对于不同颜色建立不同的线段树的思想很类似
说人话就是,对于每一个宗教,我们都给它开一棵线段树,然后路径上的查询(QS 操作,QM 操作)就在相应的宗教对应的线段树上直接查询即可
两个修改更好维护咯,单点修改就记住先清空原有信息,再赋值更新信息
点击查看代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int maxn=1e5+10;
int n,q,w[maxn],c[maxn];
vector<int> G[maxn];
int fa[maxn],son[maxn],sz[maxn],dep[maxn];
int dfn[maxn],tim,Top[maxn],rev[maxn];
struct Segment_tree{
struct node{
int l,r,sum,mx;
}tr[maxn<<5];
int rt[maxn],cnt;
void pushup(int u){
tr[u].sum=tr[tr[u].l].sum+tr[tr[u].r].sum;
tr[u].mx=max(tr[tr[u].l].mx,tr[tr[u].r].mx);
return;
}
void modify(int &u,int l,int r,int pos,int k){
if(u==0){
u=++cnt;
}
if(l==r){
tr[u].sum+=k;
tr[u].mx=max(tr[u].mx,k);
return;
}
int mid=l+r>>1;
if(pos<=mid){
modify(tr[u].l,l,mid,pos,k);
}else{
modify(tr[u].r,mid+1,r,pos,k);
}
pushup(u);
return;
}
void del(int &u,int l,int r,int pos){
if(l==r){
tr[u].sum=0;
tr[u].mx=0;
return;
}
int mid=l+r>>1;
if(pos<=mid){
del(tr[u].l,l,mid,pos);
}else{
del(tr[u].r,mid+1,r,pos);
}
pushup(u);
return;
}
int query1(int u,int l,int r,int ql,int qr){
if(ql<=l&&qr>=r){
return tr[u].sum;
}
int mid=l+r>>1,res=0;
if(ql<=mid){
res+=query1(tr[u].l,l,mid,ql,qr);
}
if(qr>mid){
res+=query1(tr[u].r,mid+1,r,ql,qr);
}
return res;
}
int query2(int u,int l,int r,int ql,int qr){
if(ql<=l&&qr>=r){
return tr[u].mx;
}
int mid=l+r>>1,res=0;
if(ql<=mid){
res=max(res,query2(tr[u].l,l,mid,ql,qr));
}
if(qr>mid){
res=max(res,query2(tr[u].r,mid+1,r,ql,qr));
}
return res;
}
}Tr;
inline void dfs1(int u,int fath){
fa[u]=fath;
dep[u]=dep[fath]+1;
sz[u]=1;
int mx=-1;
for(int v:G[u]){
if(v==fath){
continue;
}
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>mx){
mx=sz[v];
son[u]=v;
}
}
return;
}
inline void dfs2(int u,int tp){
dfn[u]=++tim;
Top[u]=tp;
rev[tim]=u;
if(son[u]==0){
return;
}
dfs2(son[u],tp);
for(int v:G[u]){
if(v==fa[u]||v==son[u]){
continue;
}
dfs2(v,v);
}
return;
}
inline int query_sum(int u,int v,int p){
int res=0;
while(Top[u]!=Top[v]){
if(dep[Top[u]]<dep[Top[v]]){
swap(u,v);
}
res+=Tr.query1(Tr.rt[p],1,n,dfn[Top[u]],dfn[u]);
u=fa[Top[u]];
}
if(dep[u]>dep[v]){
swap(u,v);
}
res+=Tr.query1(Tr.rt[p],1,n,dfn[u],dfn[v]);
return res;
}
inline int query_max(int u,int v,int p){
int res=0;
while(Top[u]!=Top[v]){
if(dep[Top[u]]<dep[Top[v]]){
swap(u,v);
}
res=max(res,Tr.query2(Tr.rt[p],1,n,dfn[Top[u]],dfn[u]));
u=fa[Top[u]];
}
if(dep[u]>dep[v]){
swap(u,v);
}
res=max(res,Tr.query2(Tr.rt[p],1,n,dfn[u],dfn[v]));
return res;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;i++){
cin>>w[i]>>c[i];
}
for(int i=1;i<=n-1;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs1(1,0);
dfs2(1,1);
for(int i=1;i<=n;i++){
Tr.modify(Tr.rt[c[i]],1,n,dfn[i],w[i]);
}
while(q--){
string s;
int x,y;
cin>>s>>x>>y;
if(s[1]=='C'){
Tr.del(Tr.rt[c[x]],1,n,dfn[x]);
Tr.modify(Tr.rt[y],1,n,dfn[x],w[x]);
c[x]=y;
}else if(s[1]=='W'){
Tr.del(Tr.rt[c[x]],1,n,dfn[x]);
Tr.modify(Tr.rt[c[x]],1,n,dfn[x],y);
w[x]=y;
}else if(s[1]=='S'){
int ans=query_sum(x,y,c[x]);
cout<<ans<<endl;
}else if(s[1]=='M'){
int ans=query_max(x,y,c[x]);
cout<<ans<<endl;
}
}
return 0;
}
T4 轻重边(P7735)
2021 年的国赛题,还热乎!
首先,树上链的信息修改,一眼树链剖分
但似乎树上直接维护轻重边不好做(根本不能做好叭!),并且树链剖分也不适用于维护树边信息,而应维护结点信息。故此,一个经典 trick,把轻重边的判定转化为一条边两端点的判定
考虑出现重边的缘由,显然在一条路径上。那么如何用结点去描述一条路径捏?一个比较神奇的想法叫做染色。对于每一次路径修改,我们都考虑给这条路径上的每一个点染色(需要区别于所有其它已有颜色)。你会惊奇地发现,这个染色操作很有正确性保障。两端点颜色相同,则该树边是重边,否则是轻边
现在转化为树上维护颜色的问题,并且要对重边计数,树链剖分的板子还是风采依旧,转化为了线段树的一个区间信息维护问题
首先对于每一个区间,线段树要记录重边数量,也就是相邻点对颜色相同的数目。这个东西怎么用小区间合并捏?显然是与小区间的左右断电有关的,所以还要记录区间左右端点的信息
剩下的就比较好维护咯!
亿些细节:
-
多测不清空,等着见祖宗
-
路径修改的时候颜色种类一定要自增 \(1\)
-
pushup和pushdown的写法需要注意一下,区间染色和区间加的写法在sum以及tag上略有区别,并且不要忘记维护区间左右端点颜色 -
线段树不建树也是要见祖宗的
-
线段树向下查询需要一个特判,也是区间左右端点惹的祸
-
考虑树链剖分向上跳跃的过程,我们不能只关注一条重链的信息,还需要关注重链的链顶与其父亲之间的颜色关系,所以也需要特判
剩下的奇奇怪怪的问题云落就不知道了捏!实在不会弄可以拿着云落的代码去对拍一下(别直接抄就行……)
点击查看代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int maxn=2e5+10;
int n,m,w[maxn],col;
vector<int> G[maxn];
int fa[maxn],son[maxn],dep[maxn],sz[maxn];
int dfn[maxn],tim,Top[maxn],rev[maxn];
struct Segment_tree{
struct node{
int l,r,col_l,col_r,sum,tag;
}tr[maxn<<2];
inline void pushup(int u){
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum+(tr[u<<1].col_r==tr[u<<1|1].col_l);
tr[u].col_l=tr[u<<1].col_l;
tr[u].col_r=tr[u<<1|1].col_r;
return;
}
inline void pushdown(int u){
if(tr[u].tag==0){
return;
}
int l=tr[u].l,r=tr[u].r,k=tr[u].tag;
int mid=l+r>>1;
tr[u<<1].sum=mid-l;
tr[u<<1|1].sum=r-mid-1;
tr[u<<1].tag=k;
tr[u<<1|1].tag=k;
tr[u<<1].col_l=k;
tr[u<<1].col_r=k;
tr[u<<1|1].col_l=k;
tr[u<<1|1].col_r=k;
tr[u].tag=0;
return;
}
inline void build(int u,int l,int r){
tr[u].l=l;
tr[u].r=r;
tr[u].tag=0;
if(l==r){
tr[u].sum=0;
tr[u].col_l=rev[l];
tr[u].col_r=rev[l];
return;
}
int mid=l+r>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
return;
}
inline void modify(int u,int ql,int qr,int k){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r){
tr[u].col_l=k;
tr[u].col_r=k;
tr[u].tag=k;
tr[u].sum=r-l;
return;
}
pushdown(u);
int mid=l+r>>1;
if(ql<=mid){
modify(u<<1,ql,qr,k);
}
if(qr>mid){
modify(u<<1|1,ql,qr,k);
}
pushup(u);
return;
}
inline int query(int u,int ql,int qr){
int l=tr[u].l,r=tr[u].r;
if(ql<=l&&qr>=r){
return tr[u].sum;
}
pushdown(u);
int mid=l+r>>1,res=0;
if(ql<=mid){
res+=query(u<<1,ql,qr);
}
if(qr>mid){
res+=query(u<<1|1,ql,qr);
}
if(ql<=mid&&qr>mid&&tr[u<<1].col_r==tr[u<<1|1].col_l){
res++;
}
return res;
}
inline int check(int u,int pos){
int l=tr[u].l,r=tr[u].r;
if(l==r){
return tr[u].col_l;
}
pushdown(u);
int mid=l+r>>1;
if(pos<=mid){
return check(u<<1,pos);
}else{
return check(u<<1|1,pos);
}
}
}Tr;
inline void init(){
for(int i=1;i<=n;i++){
G[i].clear();
}
memset(w,0,sizeof(w));
col=0;
memset(fa,0,sizeof(fa));
memset(son,0,sizeof(son));
memset(dep,0,sizeof(dep));
memset(sz,0,sizeof(sz));
memset(dfn,0,sizeof(dfn));
tim=0;
memset(rev,0,sizeof(rev));
memset(Top,0,sizeof(Top));
return;
}
inline void dfs1(int u,int fath){
fa[u]=fath;
dep[u]=dep[fath]+1;
sz[u]=1;
int mx=-1;
for(int v:G[u]){
if(v==fath){
continue;
}
dfs1(v,u);
sz[u]+=sz[v];
if(sz[v]>mx){
mx=sz[v];
son[u]=v;
}
}
return;
}
inline void dfs2(int u,int tp){
dfn[u]=++tim;
Top[u]=tp;
rev[tim]=w[u];
if(son[u]){
dfs2(son[u],tp);
}
for(int v:G[u]){
if(v==fa[u]||v==son[u]){
continue;
}
dfs2(v,v);
}
return;
}
inline void update(int u,int v){
col++;
while(Top[u]!=Top[v]){
if(dep[Top[u]]<dep[Top[v]]){
swap(u,v);
}
Tr.modify(1,dfn[Top[u]],dfn[u],col);
u=fa[Top[u]];
}
if(dep[u]>dep[v]){
swap(u,v);
}
Tr.modify(1,dfn[u],dfn[v],col);
return;
}
inline int ask(int u,int v){
int res=0;
while(Top[u]!=Top[v]){
if(dep[Top[u]]<dep[Top[v]]){
swap(u,v);
}
res+=Tr.query(1,dfn[Top[u]],dfn[u]);
if(Tr.check(1,dfn[fa[Top[u]]])==Tr.check(1,dfn[Top[u]])){
res++;
}
u=fa[Top[u]];
}
if(dep[u]>dep[v]){
swap(u,v);
}
res+=Tr.query(1,dfn[u],dfn[v]);
return res;
}
inline void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++){
w[i]=++col;
}
for(int i=1;i<=n-1;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs1(1,0);
dfs2(1,1);
Tr.build(1,1,n);
while(m--){
int opt,x,y;
cin>>opt>>x>>y;
if(opt==1){
update(x,y);
}else{
int ans=ask(x,y);
cout<<ans<<endl;
}
}
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
cin>>T;
while(T--){
init();
solve();
}
return 0;
}
后记
工作量突然变少了,还有点不适应
完结撒花!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号