1.12 下午-换根 DP & 数位 DP & 状压 DP

前言

勿让将来，辜负曾经

这是成为 DP 大佬前的考验吗……

正文

知识点

换根 DP 往往比较明显，但难在转移方程的推导，比如说板子题就有一定的思维难度。这东西的套路就是记 \(f_u\) 表示以 \(u\) 为根的答案，然后试图 \(O(1)\) 转移给 \(f_v\)（其中 \(v\) 满足 \((u,v) \in E\)）

数位 DP 可是一位重量级选手。同机房内对这个鬼东西的评价褒贬不一，反正云落觉得挺难的

某大巨：数数题！直接填数就完事咯！

状压 DP 比之上面两个东东还是友好了许多（虽然有一道题目没有独立做出来……），毕竟比较好理解。不论是二进制状压，还是其它进制的状压，它们的共性都是用一个大整数表示集合。当然，多说一嘴，刨去以状压 DP 为正解的题目，状压 DP 还可以提供一种拿部分分的思路，也许比暴搜好点？

总结来说，三种 DP 都需要熟练掌握，真是好恶心东西

一题一解

T1 STA-Station（P3478）

链接

换根板子题。

我们设 \(u\) 为根，其答案记为 \(f_u\)，这个东西可以 \(O(n)\) 算出来。然后进行转移，形如 \(f_u \to f_v\)，转移方程还是很好想的。

\(v\) 子树内部的每个点少了 \(1\) 的贡献，\(v\) 子树外部的每个点多了 \(1\) 的贡献。所以，转移方程如下：

\[f_v = f_u + n - 2 \times sz_v \]

\(sz_v\) 表示 \(v\) 子树大小

每次转移都是 \(O(1)\) 滴！时间复杂度很有保障

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+10;
int n;
vector<int> G[maxn];
int dep[maxn],sz[maxn];
int f[maxn];
inline void dfs(int u,int fath){
	dep[u]=dep[fath]+1;
	sz[u]=1;
	for(int v:G[u]){
		if(v==fath){
			continue;
		}
		dfs(v,u);
		sz[u]+=sz[v];
	}
	return;
}
inline void solve(int u,int fath){
	for(int v:G[u]){
		if(v==fath){
			continue;
		}
		f[v]=f[u]+n-sz[v]*2;
		solve(v,u);
	}
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	for(int i=1;i<=n-1;i++){
		int u,v;
		cin>>u>>v;
		G[u].push_back(v);
		G[v].push_back(u);
	}
	dfs(1,0);
	for(int i=1;i<=n;i++){
		f[1]+=dep[i];
	}
	solve(1,0);
	int mx=0,ans=0;
	for(int i=1;i<=n;i++){
		if(f[i]>mx){
			mx=f[i];
			ans=i;
		}
	}
	cout<<ans<<endl;
	return 0;
}

T2 Nearby Cows G（P3047）

链接

又是被绿题爆切的一天……

这个题出的很有迷惑性，题面并没有说和根有关，而是隐晦地表述——“距离不超过 \(k\) 的点权和”。其实说到距离这个东西，就应该往换根那个方向去靠拢

记 \(f_{u,i}\) 表示 \(u\) 结点的答案，发现并不好转移。因为当我们确定根结点的位置的时候，距离为 \(k\) 会出现两种情况，子树外和子树内，显然子树外的部分极其不好转移

那么考虑加入一个辅助数组，记 \(g_{u,i}\) 表示子树内距离不超过 \(k\) 的点权和，这个东西显然可以 \(O(n \times k)\) 初始化出来

方程大概长成这个样子：

\[g_{u,i} = c_u + \sum_{v \in son_u,i \in [1,k]} g_{v,i-1} \]

恭喜我们完成了这道题的 \(50 \%\)！现在比较麻烦的一件事就是怎么去转移 \(f\) 数组

首先 \(f_{u,i}\) 肯定包含 \(g_{u,i}\)，代码实现上建议直接赋初值

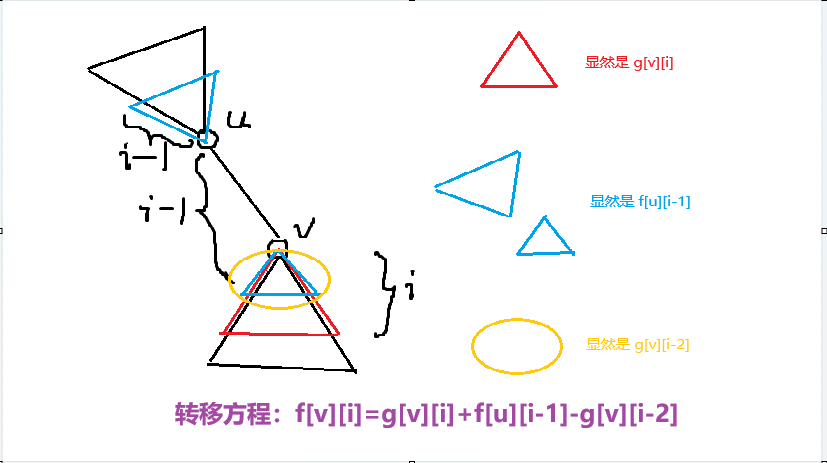
如上图，简单容斥即可！

点击查看代码

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int maxn=1e5+5,maxk=25;
int n,k;
vector<int> G[maxn];
int c[maxn];
int g[maxn][maxk],f[maxn][maxk];
inline void dfs(int u,int fath){
	for(int i=0;i<=k;i++){
		g[u][i]=c[u];
	}
	for(int v:G[u]){
		if(v==fath){
			continue;
		}
		dfs(v,u);
		for(int i=1;i<=k;i++){
			g[u][i]+=g[v][i-1];
		}
	}
	return;
}
inline void solve(int u,int fath){
	for(int v:G[u]){
		if(v==fath){
			continue;
		}
		f[v][1]+=g[u][0];
		for(int i=2;i<=k;i++){
			f[v][i]+=(f[u][i-1]-g[v][i-2]);
		}
		solve(v,u);
	}
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>k;
	for(int i=1;i<=n-1;i++){
		int u,v;
		cin>>u>>v;
		G[u].push_back(v);
		G[v].push_back(u);
	}
	for(int i=1;i<=n;i++){
		cin>>c[i];
	}
	dfs(1,0);
	for(int u=1;u<=n;u++){
		for(int i=0;i<=k;i++){
			f[u][i]=g[u][i];
		}
	}
	solve(1,0);
	for(int u=1;u<=n;u++){
		cout<<f[u][k]<<endl;
	}
	return 0;
}

T3 连珠线（P3647）

链接

Honestly，云落真不想写这个破题好题的题解……

观察性质

蓝线的两种构造——为了方便描述，左图称为“三角”结构，右图称为“链”结构

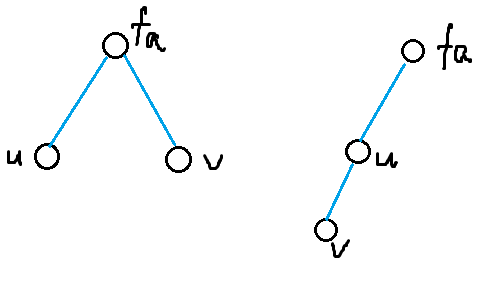
然而类似于下图的会不合法

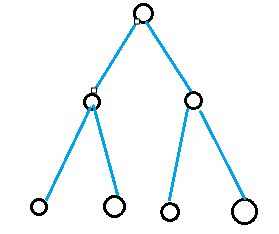
因为它的红线的连法是有要求的——是每次向点集插入，而不是凭空捏造一个——也就是说不会出现两个及以上的“三角”结构

再做一步转化，因为不存在两个及以上的“三角”结构，所以我们总能通过指定根结点的形式，使得整棵树上不存在“三角”结构

所以题目就转化为：对于不同指定的根结点，保证全是树上只存在“链”结构，蓝色边边权和的最大值

DP！

似乎嗅到了一丝换根的气味……

Wait for a minute，也许我们应该先考虑指定一个根结点的时候的答案计算

很显然应该设计一个类似树形 DP 的东西，记 \(f_u\) 表示 \(u\) 子树内的答案，好消息，时间复杂度没啥问题，坏消息，没法转移。

Why？因为“链”结构是存在两种“地位”不同的点的，一种是端点，一种是中点。端点可以直接转移，在刚才的状态设计下不会存在后效性。然而如果结点 \(u\) 是中点，结点 \(u\) 所在的“链”结构就会横穿 \(u\) 子树……然后就寄了

所以就简简单单加一维度：记 \(f_{u,0/1}\) 表示 \(u\) 不是/是 中点时 \(u\) 子树内的答案贡献

为了方便表述，记无向边 \((u,v)\) 的边权为 \(w(u,v)\)

转移方程形如：

\[f_{u,0} = \sum_{v \in son_u} \max(f_{v,0},f_{v,1}+w(u,v)) \\ f_{u,1} = f_{u,0} + \max_{v \in son_u} \lbrace f_{v,0} + w(u,v) - \max(f_{v,0},f_{v,1}+w(u,v))\rbrace \]

固定根结点的答案计算已经弄完了，接下来，是换根时间！（~~好中二~~）

我们记 \(g_{u,0}\) 表示以 \(u\) 为根的答案，\(h_{u,0/1}\) 表示 \(u\) 不是/是 中点时一部分（如下图）的答案

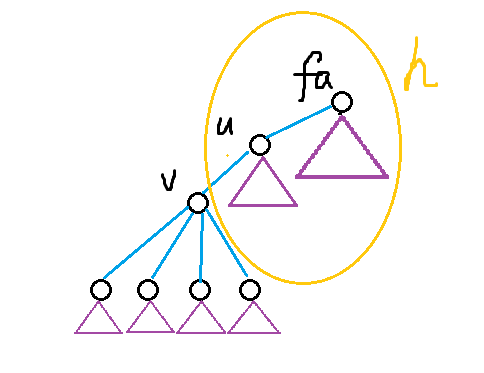
Q：为什么没有 \(g_{u,1}\)？

A：\(u\) 都是树根了怎么还能作为一个“链”结构的中点捏……

考虑通过 \(f\) 转移 \(h\)，再通过 \(f,h\) 转移 \(g\)。（温馨提示：建议理解透彻最上方固定根的两个转移之后再来食用接下来的转移方程）

对于 \(h_{u,0/1}\)，有转移方程：

\[h_{u,0} = g_{u,0} - \max (f_{v,0},f_{v,1}+w(v,u)) \\ h_{u,1} = h_{u,0} + \max (\max_{i \in son_u \land i \neq v} \lbrace f_{i,0} + w(i,u) - \max(f_{i,0},f_{i,1}+w(i,u)) \rbrace,h_{fa,0} + w(fa,u) - \max(h_{fa,0},h_{fa,1}+w(fa,u))) \]

哎，好累……给一些上面式子的说明：

首先，我们需要注意到，\(h\) 数组的调用总是慢于 \(g\) 数组的更新的。什么意思，就是我们要给 \(g_{v,0}\) 更新的时候，需要调用的是 \(h_{u,0/1}\)，所以第一个式子带 \(g\) 的转移没有问题

其次，上面两个式子中重复出现了一个东西，形如 \(\max(f_{v,0},f_{v,1}+w(v,u))\)。这个东西就是 \(v\) 子树向 \(u\) 转移时能给出的最大贡献。什么意思？\(v\) 结点的可能是中点也可能不是中点，在两种情况下，我们要取 \(v\) 子树中最大的一种方案贡献给 \(u\) 子树。如果不是中点，转移没有什么特别，万事大吉！如果是中点，意味着 \((u,v)\) 这条边一定会计入贡献，所以要比较 \(f_{v,0}\) 与 \(f_{v,1}+w(u,v)\)，取较大值贡献上去

如果你可以完全理解一开始 \(f_{u,1}\) 的更新方式，一定也能理解 \(h_{u,1}\)，可以跳过这段废话。

接下来，说点废话。\(f_{u,1}\) 如何贡献，首先当 \(u\) 不是中点的时候，贡献为 \(f_{u,0}\)。那么当 \(u\) 被我们指定为“链”结构的中点时，对其子树内部的影响就是，\(u\) 要在所有儿子 \(v\) 中挑选一个价值最大的儿子作为“链”结构的下端点。

什么是价值最大？这个东西不太好定义，但是我们可以从结果的角度出发，逆推价值。什么意思嘞？就是当我们选中 \(v\) 的时候，\(v\) 子树给 \(u\) 的贡献形如 \(f_{v,0} + w(u,v)\)，而它本来的贡献是 \(\max(f_{v,0},f_{v,1}+w(v,u))\)。价值的概念就出来了，就是贡献的变化量！也就是说，我们只需要选中上述初末状态的差值最大的儿子 \(v\) 贡献上去即可

\(f_{u,1}\) 理解之后，回过头来看 \(h_{u,1}\)，显然在 \(v\) 为根的情况下，什么东西可以转移给 \(h_{u,1}\)，显然是以 \(1\) 为根意义下，\(u\) 的除 \(v\) 以外所有儿子以及 \(u\) 的父亲。分别取最大值，最后再取最大值贡献即可！

说了这么多辅助数组，该更新答案数组力！\(g_{v,0}\) 的转移方程形如——

\[g_{v,0} = f_{v,0} + \max(h_{u,0},h_{u,1}+w(u,v)) \]

思路大概就这样……但是这毕竟是口胡……

细节与代码实现

次大值

其实当初根本没有想到需要更新这个东西，毕竟转移方程式子里面清一色的 \(\max\)，然后就各种样例不过，各种听取 WA 声一片……

你发现在更新 \(h\) 的时候在一个不为人知的小角落里藏匿着这么个东西 \(i \in son_u \land i \neq v\)，也就是说我们在预处理 \(f\) 数组以及最大价值的儿子的时候会出事。因为有可能我们要转移的 \(v\) 就是价值最大的儿子……

所以要维护一个次大值，以备不时之需

边权存储

还是 \(h\) 的转移过程惹的祸，注意到边权调用里会出现什么东西呢，诶嘿就是这玩意——\(w(fa,u)\)，所以要开一个 \(W\) 数组，\(W_u\) 自然表示 \(w(u,fa)\) 咯！

根结点

有个细节需要注意——\(1\) 号节点是没有 \(fa\) 的，需要特判

剩下的没啥了，照着转移方程誊抄就可以力

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e5+5,inf=9e18;
int n;
int head[maxn],tot;
struct Edge{
	int to,nxt,val;
}e[maxn<<1];
int W[maxn];
int mx1[maxn],son1[maxn],mx2[maxn],son2[maxn];
int f[maxn][2],g[maxn][2],h[maxn][2];
inline void add(int u,int v,int w){
	e[++tot].to=v;
	e[tot].val=w;
	e[tot].nxt=head[u];
	head[u]=tot;
	return;
}
inline void dfs(int u,int fath){
	mx1[u]=-inf;
	mx2[u]=-inf;
	son1[u]=0;
	son2[u]=0;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to,w=e[i].val;
		if(v==fath){
			continue;
		}
		W[v]=w;
		dfs(v,u);
		f[u][0]+=max(f[v][0],f[v][1]+w);
		int V=f[v][0]+w-max(f[v][0],f[v][1]+w);
		if(mx1[u]<V){
			son2[u]=son1[u];
			mx2[u]=mx1[u];
			son1[u]=v;
			mx1[u]=V;
		}else if(mx2[u]<V){
			son2[u]=v;
			mx2[u]=V;
		}
	}
	f[u][1]=f[u][0]+mx1[u];
	return;
}
inline void solve(int u,int fath){
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to,w=e[i].val;
		if(v==fath){
			continue;
		}
		if(son1[u]==v){
			swap(mx1[u],mx2[u]);
			swap(son1[u],son2[u]);
		}
		h[u][0]=g[u][0]-max(f[v][0],f[v][1]+w);
		h[u][1]=h[u][0]+mx1[u];
		if(fath!=-1){
			h[u][1]=max(h[u][1],h[u][0]+h[fath][0]+W[u]-max(h[fath][0],h[fath][1]+W[u]));
		}
		g[v][0]=f[v][0]+max(h[u][0],h[u][1]+w);
		if(mx1[u]<mx2[u]){
			swap(mx1[u],mx2[u]);
			swap(son1[u],son2[u]);
		}
		solve(v,u);
	}
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	for(int i=1;i<=n-1;i++){
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,w);
		add(v,u,w);
	}
	dfs(1,-1);
	g[1][0]=f[1][0];
	solve(1,-1);
	int ans=0;
	for(int i=1;i<=n;i++){
		ans=max(ans,g[i][0]);
	}
	cout<<ans<<endl;
	return 0;
}

T4 建造军营（P8867）

链接

这位更是重量级……我嘞个超绝边双缩点加树形 DP 统计答案，真就 \(DAY^{-1}\)

边双缩点是显然的，因为只有当对方炸毁无向图上的桥，才会使得图不连通。自然地，一个边双联通分量内部是可以统一计算的，所以考虑边双缩点

缩点之后显然是一个树结构，然后怎么计算答案捏？

给题意做一步转化，可以理解为在缩点后的树上选中一些关键点，然后再选取一个边集，使得任意两个关键点的路径所经过的边都是这个边集的元素

当然，因为这棵树上是有一些边双缩点之后的结点，所以要记录一下每个树上的结点到底内部有多少个结点多少条边

上述准备工作做完后，接下来 DP 计算方案！云落试图使用树形 DP，但奈何根本就没有根结点，于是乎又双叒叕指定了 \(1\) 号结点为根结点了……

记 \(f_{u,0/1}\) 表示 \(u\) 子树内 没有/有 军营的方案数，日常转移不了。维度好像不是很好加，那么就加限制条件吧！记 \(f_{u,0/1}\) 表示以 \(u\) 为根的子树中 没有/有 军营的方案数，要求如果存在军营 \(v\)，则边集必须包含路径 \((u,v)\) 上的所有边

为了方便表述，记 \(s_u\) 表示 \(u\) 子树内的边数（Warning：这个不是指树边的数目，是包含边双连通分量内部的边数的），\(V_u\) 表示树上结点 \(u\) 所对应的边双连通分量的结点数，\(E_u\) 表示树上结点 \(u\) 所对应的边双连通分量的边数

\(V,E\) 都可以在边双缩点的时候统计出来，\(s\) 也可以 DFS 预处理

先不说转移捏，先考虑答案计算……答案计算有点灵性捏。先让云落偷一张图

（来自 luogu 题解区第一篇）

可以注意到，上述情况会重复计算。为了避免重复，我们计算方案的时候这么考虑，强制 \(u\) 子树外没有任何军营且，强制不选无向边 \((u,fa_u)\)，那么答案就好算了，形如：

\[ans = \Big ( f_{1,1} + \sum_{u=2}^{n} f_{u,1} \times 2^{s_1-s_u-1} \Big ) \bmod 1000000007 \]

提示一点——\(f_{1,1}\) 的特判

初始化比较显然，\(f_{u,0}=2^{E_u},f_{u,1}=2^{E_u+V_u}-f_{u,0}\)，接下来是最快乐的转移环节

\(f_{u,0}\) 是好转移的，因为子树内不存在军营，所以只需考虑本质不同的选边方案即可，显然有：

\[{f'}_{u,0} \gets f_{u,0} \times \prod_{v \in son_u} (2 \times f_{v,0}) \]

注：累乘号里面的 \(2\) 表示边 \((u,v)\) 是否选

\(f_{u,1}\) 也是好转移的，经典套路——每次维护一个由 \(v\) 组成的前缀，先给转移方程：

\[{f'}_{u,1} \gets f_{u,0} \times f_{v,1} + f_{u,1} \times [2 \times f_{v,0} + f_{v,1}] \]

简单解释一下，如果前缀没有建造任何军营（即 \(f_{u,0}\)），那么如果想要有贡献，\(v\) 子树必须建造军营，依据乘法原理，直接 \(\times f_{v,1}\) 即可；而如果前缀已经存在军营，那么 \(v\) 子树的填入方案就可以放飞自我了。如果不建造军营，\((u,v)\) 边可选亦可不选；如果建造军营，就必须选。两种情况是并列的，加法原理直接统计即可

注意下细节：要先更新 \(f_{u,1}\) 后更新 \(f_{u,0}\) 哦！

总体来说不是很难，云落认为比上一道题略简单点捏（但是边双缩点好像是省选难度的算法？）

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=5e5+5,maxm=1e6+5,mod=1e9+7;
int n,m;
int head[maxn],tot;
struct Edge{
	int to,nxt;
}e[maxm<<1];
int dfn[maxn],tim,low[maxn],col[maxn];
bool vis[maxn];
int stk[maxn],tp;
vector<int> G[maxn];
int tol,E[maxn],V[maxn],s[maxn];
int f[maxn][2],ans;
inline void add(int u,int v){
	e[++tot].to=v;
	e[tot].nxt=head[u];
	head[u]=tot;
	return;
}
inline int qpow(int a,int b){
	int res=1;
	while(b){
		if(b&1){
			res=res*a%mod;
		}
		a=a*a%mod;
		b>>=1;
	}
	return res;
}
inline void tarjan(int u,int fa){
	dfn[u]=low[u]=++tim;
	vis[u]=true;
	stk[++tp]=u;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa){
			continue;
		}
		if(!dfn[v]){
			tarjan(v,u);
			low[u]=min(low[u],low[v]);
		}else if(vis[v]){
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(dfn[u]==low[u]){
		tol++;
		int x;
		do{
			x=stk[tp--];
			vis[x]=false;
			col[x]=tol;
			V[tol]++;
		}while(u!=x);
	}
	return;
}
inline void dfs(int u,int fa){
	s[u]=E[u];
	for(int v:G[u]){
		if(v==fa){
			continue;
		}
		dfs(v,u);
		s[u]+=(s[v]+1);
	}
	return;
}
inline void dp(int u,int fa){
	for(int v:G[u]){
		if(v==fa){
			continue;
		}
		dp(v,u);
		f[u][1]=(f[u][1]*((f[v][0]*2%mod+f[v][1])%mod)%mod+f[u][0]*f[v][1]%mod)%mod;
		f[u][0]=f[u][0]*(f[v][0]*2%mod)%mod;
	}
	if(u==1){
		ans=(ans+f[u][1])%mod;
	}else{
		ans=(ans+f[u][1]*qpow(2,s[1]-s[u]-1)%mod)%mod;
	}
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	tarjan(1,0);
	for(int u=1;u<=n;u++){
		for(int i=head[u];i;i=e[i].nxt){
			int v=e[i].to;
			if(col[u]!=col[v]){
				G[col[u]].push_back(col[v]);
			}else{
				E[col[u]]++;
			}
		}
	}
	for(int i=1;i<=tol;i++){
		E[i]>>=1;
		f[i][0]=qpow(2,E[i]);
		f[i][1]=(qpow(2,V[i]+E[i])-f[i][0]+mod)%mod;
	}
	dfs(1,0);
	dp(1,0);
	cout<<ans<<endl;
	return 0;
}

T5 Minimax（P5298）

链接

云落超级喜爱线段树合并——

正如上文所述，这个题又是一道线段树合并优化 DP 的题目，并且和 P6773 非常像，都是经典的线段树合并维护前缀和

一眼树形 DP，还是套路的设 \(f_u\) 表示 \(u\) 子树的答案，发现取值这一维度根本提现不了，索性加一维度，记 \(f_{u,i}\) 表示 \(u\) 子树已经处理完毕，并且 \(u\) 取值为 \(i\) 的概率

注意到题目描述中每个结点最多有两个子结点，也就是说，这是一棵二叉树。那么最大值（或最小值）只能从左儿子或者右儿子贡献，转移方程大概也可以写出来咯！

为了方便表述，记 \(ls\) 表示左儿子，\(rs\) 表示右儿子，转移方程形如：

\[f_{u,i} = f_{ls,i} \times \Big (p_i \times \sum_{j=1}^{i-1} f_{rs,j} + (1-p_i) \times \sum_{j=i+1}^{m} f_{rs,j} \Big ) + f_{rs,i} \times \Big ( p_i \times \sum_{j=1}^{i-1} f_{ls,j} + (1-p_i) \times \sum_{j=i+1}^{m} f_{ls,j} \Big ) \]

显然时间复杂度 \(O(n^2)\)

就上面这么一坨，注意到又是一个静态的树上信息维护，并且 \(f_{u,i}\) 的很多地方是没有值的，以及根据我们做题的经验，看到求和号就会想到前缀和，我们会想到线段树合并优化求和的部分

可能 debug 难度有点大，又是前缀和又是后缀和的……

时间复杂度 \(O(n \log n)\)

点击查看代码

#include<iostream>
#include<algorithm>
#include<vector>
#define int long long
using namespace std;
const int maxn=6e5+10,mod=998244353,inv=796898467,inf=1e9;
int n,val[maxn],sz[maxn];
int head[maxn],tot;
struct Edge{
    int to,nxt;
}e[maxn<<1];
int rt[maxn],cnt,s1,s2,t1,t2;
struct Segment_tree{
    struct node{
        int l,r,sum,tag;
    }tr[maxn<<5];
    int d[maxn];
    void pushup(int u){
        tr[u].sum=(tr[tr[u].l].sum+tr[tr[u].r].sum)%mod;
        return;
    }
    void pushdown(int u){
        if(u==0){
            return;
        }
        if(tr[u].tag==1){
            return;
        }
        tr[tr[u].l].sum=tr[tr[u].l].sum*tr[u].tag%mod;
        tr[tr[u].l].tag=tr[tr[u].l].tag*tr[u].tag%mod;
        tr[tr[u].r].sum=tr[tr[u].r].sum*tr[u].tag%mod;
        tr[tr[u].r].tag=tr[tr[u].r].tag*tr[u].tag%mod;
        tr[u].tag=1;
        return;
    }
    void modify(int &u,int l,int r,int pos,int k){
        if(u==0){
            u=++cnt;
            tr[u].tag=1;
        }
        if(l==r){
            tr[u].sum=(tr[u].sum+k)%mod;
            return;
        }
        pushdown(u);
        int mid=l+r>>1;
        if(pos<=mid){
            modify(tr[u].l,l,mid,pos,k);
        }else{
            modify(tr[u].r,mid+1,r,pos,k);
        }
        pushup(u);
        return;
    }
    int num;
    int query(int u,int l,int r){
        if(u==0){
            return 0;
        }
        if(l==r){
            return (++num)*l%mod*tr[u].sum%mod*tr[u].sum%mod;
        }
        pushdown(u);
        int mid=l+r>>1,res=0;
        res=(res+query(tr[u].l,l,mid))%mod;
        res=(res+query(tr[u].r,mid+1,r))%mod;
        return res;
    }
    int merge(int x,int y,int l,int r,int v){
        if(x==0&&y==0){
            return 0;
        }
        if(x==0){
            t2=(t2+tr[y].sum)%mod;
            tr[y].sum=tr[y].sum*((t1*v%mod+(s1-t1+mod)%mod*(1-v+mod)%mod)%mod)%mod;
            tr[y].tag=tr[y].tag*((t1*v%mod+(s1-t1+mod)%mod*(1-v+mod)%mod)%mod)%mod;
            return y;
        }
        if(y==0){
            t1=(t1+tr[x].sum)%mod;
            tr[x].sum=tr[x].sum*((t2*v%mod+(s2-t2+mod)%mod*(1-v+mod)%mod)%mod)%mod;
            tr[x].tag=tr[x].tag*((t2*v%mod+(s2-t2+mod)%mod*(1-v+mod)%mod)%mod)%mod;
            return x;
        }
        if(l==r){
            t1=(t1+tr[x].sum)%mod;
            t2=(t2+tr[y].sum)%mod;
            int tmp=tr[x].sum*tr[y].sum%mod,res=0;
            res=res+tr[x].sum*((t2*v%mod+(s2-t2+mod)%mod*(1-v+mod)%mod)%mod)%mod;
            res=res+tr[y].sum*((t1*v%mod+(s1-t1+mod)%mod*(1-v+mod)%mod)%mod)%mod;
            tr[x].sum=res;
            return x;
        }
        pushdown(x);
        pushdown(y);
        int mid=l+r>>1;
        tr[x].l=merge(tr[x].l,tr[y].l,l,mid,v);
        tr[x].r=merge(tr[x].r,tr[y].r,mid+1,r,v);
        pushup(x);
        return x;
    }
}Tr;
inline void add(int u,int v){
    e[++tot].to=v;
    e[tot].nxt=head[u];
    head[u]=tot;
    sz[u]++;
    return;
}
inline void dfs(int u){
    if(sz[u]==0){
        return;
    }
    if(sz[u]==1){
        int v=e[head[u]].to;
        dfs(v);
        rt[u]=rt[v];
        return;
    }
    int ls=e[head[u]].to,rs=e[e[head[u]].nxt].to;
    dfs(ls);
    dfs(rs);
    s1=Tr.tr[rt[ls]].sum;
    s2=Tr.tr[rt[rs]].sum;
    t1=0;
    t2=0;
    rt[u]=Tr.merge(rt[ls],rt[rs],1,inf,val[u]);
    return;
}
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++){
        int fa;
        cin>>fa;
        if(fa){
            add(fa,i);
        }
    }
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        if(head[i]==0){
            Tr.modify(rt[i],1,inf,x,1);
        }else{
            val[i]=x*inv%mod;
        }
    }
    dfs(1);
    int ans=Tr.query(rt[1],1,inf);
    cout<<ans<<endl;
    return 0;
}

T6 windy 数（P2657）

链接

数位 DP 的第一道题目呢，还是比较板子的。云落建议多写写记忆化搜索，正经的动态规划的循环写法实在是太不美观了……

圆规正传，对于这道题目，先套路性的把查询区间的个数转化为类似前缀和相减的形式。然后只需要计算区间 \([1,x]\) 中存在多少个合法的 windy 数即可

考虑试填法。注意到我们试填 windy 数是有上界 \(x\) 的约束的，所以考虑从高位向低位试填。那么自然会引出几个参数，试填到第几位 \(pos\)，是否与上界贴合 \(lim\)，前导 \(0\) 判断 \(zero\)

然后再回到 windy 数的性质，很明显当前试填的数字是和上一个试填的数字有关，所以记录一个 \(lst\) 表示上一位填的数字

剩下的就是直接搜的事了，记得加个记忆化！（云落也写了循环写法）

记搜递归：

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=15;
int l,r,a[maxn];
int f[maxn][maxn][2][2];
inline int dfs(int pos,int lst,bool lim,bool zero){
	if(!pos){
		return 1;
	}
	if(~f[pos][lst][lim][zero]){
		return f[pos][lst][lim][zero];
	}
	int res=0;
	for(int i=0;i<=9;i++){
		if((i<=a[pos]||!lim)&&(abs(i-lst)>=2||zero)){
			res+=dfs(pos-1,i,lim&&(i==a[pos]),zero&&(!i));
		}
	}
	f[pos][lst][lim][zero]=res;
	return res;
}
inline int solve(int x){
	memset(f,-1,sizeof(f));
	memset(a,0,sizeof(a));
	int tol=0;
	while(x){
		a[++tol]=x%10;
		x/=10;
	}
	return dfs(tol,10,1,1);
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>l>>r;
	cout<<solve(r)-solve(l-1)<<endl;
	return 0;
}

DP 循环（简单说一下，\(dp_{i,j}\) 表示长度为 \(i\) 最高位为 \(j\) 的 windy 数个数，预处理很显然。答案计算分为三部分，windy 数长度不够的，windy 数最高位填的数小于上界的，剩下的奇奇怪怪的东东）

点击查看代码

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=10;
int l,r,a[maxn],dp[maxn][maxn];
inline void init(){
    for(int i=0;i<=9;i++){
        dp[1][i]=1;
    }
    for(int i=2;i<=10;i++){
        for(int j=0;j<=9;j++){
            for(int k=0;k<=9;k++){
                if(abs(j-k)>=2){
                    dp[i][j]+=dp[i-1][k];
                }
            }
        }
    }
    return;
}
inline int query(int x){
    memset(a,0,sizeof(a));
    int len=0,ans=0;
    while(x){
        a[++len]=x%10;
        x/=10;
    }
    for(int i=1;i<=len-1;i++){
        for(int j=1;j<=9;j++){
            ans+=dp[i][j];
        }
    }
    for(int i=1;i<a[len];i++){
        ans+=dp[len][i];
    }
    for(int i=len-1;i>=1;i--){
        for(int j=0;j<=a[i]-1;j++){
            if(abs(j-a[i+1])>=2){
                ans+=dp[i][j];
            }
        }
        if(abs(a[i+1]-a[i])<2){
            break;
        }
    }
    return ans;
}
int main(){
    init();
    cin>>l>>r;
    cout<<query(r+1)-query(l)<<endl;
    return 0;
}

T7 数字计数（P2602）

[链接]（https://www.luogu.com.cn/problem/P2602）

云落用了点小学奥数就给它水过去了，不推荐哈，还是老老实实写数位 DP 比较好

高端的 oier 是如何优雅地切掉这道题呢？应当是这样的——

仍旧是考虑试填法，仍旧是上界限制，所以从高位向低位试填，记当前位为 \(pos\)。当然也会有 \(pos\) 的好伙伴——\(lim,zero\)，分别表示是否贴合上界以及是否存在前导 \(0\)
这个题目比较灵性，要求我们对每个数码都统计出现次数，那索性就把这个需要计算个数的数码作为一个参数 \(num\) 传进去
最后维护一个参数 \(sum\) 表示试填完整结束之后的答案

还是套路的试填与记搜……（考察考察代码基本功呢！）

记搜递归：

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=15;
int l,r;
int a[maxn],f[maxn][maxn];
inline int dfs(int pos,bool lim,bool zero,int num,int sum){
	if(pos==0){
		return sum;
	}
	if(!lim&&!zero&&~f[pos][sum]){
		return f[pos][sum];
	}
	int res=0;
	for(int i=0;i<=9;i++){
		if(!lim||i<=a[pos]){
			res+=dfs(pos-1,lim&&(i==a[pos]),zero&&(!i),num,sum+((!zero||i)&&(i==num)));
		}
	}
	if(!lim&&!zero){
		f[pos][sum]=res;
	}
	return res;
}
inline int solve(int x,int num){
	memset(f,-1,sizeof(f));
	int tol=0;
	while(x){
		a[++tol]=x%10;
		x/=10;
	}
	return dfs(tol,1,1,num,0);
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>l>>r;
	for(int i=0;i<=9;i++){
		cout<<solve(r,i)-solve(l-1,i)<<' ';
	}
	return 0;
}

小奥乱搞：

点击查看代码

#include<iostream>
#include<cstring>
#define int long long
using namespace std;
const int maxn=16;
int a,b;
int f[maxn],p[maxn],s[maxn];
int cnta[maxn],cntb[maxn],cnt[maxn];
inline void solve(int x){
    memset(cnt,0,sizeof(cnt));
    int len=0;
    int tmp=x;
    while(tmp){
        s[++len]=tmp%10;
        tmp/=10;
    }
    for(int i=len;i;i--){
    	for(int j=0;j<=9;j++){
    		cnt[j]+=(s[i]*f[i-1]);
		}
		for(int j=0;j<s[i];j++){
			cnt[j]+=p[i-1];
		}
		cnt[s[i]]+=(x%p[i-1]+1);
		cnt[0]-=p[i-1];
	}
	return;
}
signed main(){
	p[0]=1;
    for(int i=1;i<=15;i++){
    	p[i]=p[i-1]*10;
	}
    for(int i=1;i<=15;i++){
    	f[i]=f[i-1]*10+p[i-1];
	}
    cin>>a>>b;
    solve(a-1);
    for(int i=0;i<=9;i++){
    	cnta[i]=cnt[i];
	}
    solve(b);
    for(int i=0;i<=9;i++){
    	cntb[i]=cnt[i];
	}
    for(int i=0;i<=9;i++){
    	cout<<cntb[i]-cnta[i]<<' ';
	}
    return 0;
}

T8 花神的数论题（P4317）

链接

就这么个东西，组合数随便搞搞就能干过去……

然而我们要选择数位 DP，虽然码量略大于组合数，但思维难度还是比较平易近人的

参数 \(pos,lim\) 就不说了，都是数位 DP 的老朋友了。注意到这个题的答案贡献计算与 \(\text{popcount}\) 有关，所以需要维护一个 \(sum\) 表示试填了多少个 \(1\)

实现细节：

数位 DP 中答案应赋初值为 \(1\)，否则，嘻嘻

开 long long 以及取模

不知道各位大巨有没有犯这个错误，云落一开始 solve 的时候转成十进制力

记搜递归：

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=65,mod=1e7+7;
int n;
int a[maxn],f[maxn][maxn];
inline int dfs(int pos,bool lim,int sum){
	if(!pos){
		return max(1ll,sum);
	}
	if(!lim&&~f[pos][sum]){
		return f[pos][sum];
	}
	int up=1ll;
	if(lim){
		up=a[pos];
	}
	int res=1ll;
	for(int i=0;i<=up;i++){
		res=(res*dfs(pos-1,lim&&i==up,sum+i))%mod;
	}
	if(!lim){
		f[pos][sum]=res;
	}
	return res;
}
inline int solve(int x){
	int tol=0;
	memset(a,0,sizeof(a));
	memset(f,-1,sizeof(f));
	while(x){
		a[++tol]=x&1;
		x>>=1;
	}
	return dfs(tol,1,0);
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	cout<<solve(n)<<endl;
	return 0;
}

组合递推（还是简单说一下，每次去找 \(sum(i)\) 的出现次数，直接累成起来。仍旧是要对区间 \([1,2^{\lfloor \log n \rfloor}]\) 以及剩余的部分分别计算贡献。需要注意的是，预处理组合数的时候，需要欧拉定理降幂——模数是 \(10000007\) 不是一个质数）：

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=65,mod=1e7+7,phi=9988440;
int n;
int C[maxn][maxn];
inline int lg(int x){
	if(x==1){
		return 0ll;
	}
	return lg(x>>1)+1ll;
}
inline void init(){
	for(int i=0;i<=lg(n);i++){
		C[i][0]=1ll;
		for(int j=1;j<=i;j++){
			C[i][j]=(C[i-1][j]+C[i-1][j-1])%phi;
		}
	}
	return;
}
inline int qpow(int a,int b){
	int res=1ll;
	while(b){
		if(b&1){
			res=res*a%mod;
		}
		a=a*a%mod;
		b>>=1;
	}
	return res;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	n++;
	init();
	int ans=1ll,cnt=0;
	while(n){
		int cal=lg(n);
		if(cnt){
			ans=ans*cnt%mod;
		}
		for(int i=1;i<=cal;i++){
			ans=ans*qpow(i+cnt,C[cal][i])%mod;
		}
		cnt++;
		n-=(1ll<<cal);
	}
	cout<<ans<<endl;
	return 0;
}

T9 Sam 数（P2106）

链接

还是熟悉的配方，数位 DP 走一波

记 \(f_{i,j}\) 表示长度为 \(i\)，且当前位为 \(j\) 的 Sam 数个数，方程如下：

\[f_{i,j} = \sum_{k = \max(0,j-2)}^{\min(9,j+2)} f_{i-1,k} \]

然而 \(k \le 10^18\)，非常的丧心且病狂，时间复杂度直接寄了。于是乎考虑优化，注意到这个转移，似乎可以用矩阵形式来刻画（其实就是一种斐波那契数列的变式），所以直接上矩阵。矩阵加速递推后，时间复杂度就没问题咯！

数位 DP 的题目会越做越顺的，嘻嘻

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=15,mod=1e9+7;
int k;
struct Matrix{
    int n,m,a[maxn][maxn];
    friend Matrix operator * (Matrix A,Matrix B){
        Matrix C;
        C.n=A.n;
        C.m=B.m;
        memset(C.a,0,sizeof(C.a));
        for(int i=0;i<C.n;i++){
            for(int j=0;j<C.m;j++){
                for(int k=0;k<A.m;k++){
                    C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j]%mod)%mod;
                }
            }
        }
        return C;
    }
}s,res;
Matrix qpow(Matrix A,int b){
    Matrix P;
    P.n=A.n;
    P.m=A.m;
    memset(P.a,0,sizeof(P.a));
    for(int i=0;i<P.n;i++){
        P.a[i][i]=1;
    }
    while(b){
        if(b&1){
            P=P*A;
        }
        A=A*A;
        b>>=1;
    }
    return P;
}
inline void init(){
	s.n=1;
	s.m=10;
	memset(s.a,0,sizeof(s.a));
	for(int i=1;i<=9;i++){
		s.a[0][i]=1;
	}
	res.n=10;
	res.m=10;
	memset(res.a,0,sizeof(res.a));
	for(int i=0;i<=9;i++){
		for(int j=0;j<=9;j++){
			if(abs(i-j)<=2){
				res.a[i][j]=1;
			}
		}
	}
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>k;
	if(k==1){
		cout<<10<<endl;
		return 0;
	}
	init();
	res=s*qpow(res,k-1);
	int ans=0;
	for(int i=0;i<=9;i++){
		ans=(ans+res.a[0][i]%mod)%mod;
	}
	cout<<ans<<endl;
	return 0;
}

T10 互不侵犯（P1896）

链接

换根 DP 和数位 DP 暂时告一段落，接下来是状压 DP 时间！

互不侵犯也是经典~~臭名昭著~~的状压 DP 题。娇小的数据范围，但是又是暴搜不可过的鬼东西，往往都是状压 DP

注意到每次我们向棋盘里放置一个国王之后会对后面的国王放置产生影响。所以一些多项式复杂度的朴素 DP 可能在这道题目并不适用，那么注意到 \(n \le 9\)，可以尝试去把每一行格子内是否放置国王的情况状压，通过上一行转移至下一行

大体思路出来了，开始状态设计。记 \(f_{i,j,k}\) 表示考虑到第 \(i\) 行，且第 \(i\) 行状态为 \(j\)，共计放了 \(k\) 个国王的方案数

在说初始化以及转移方程之前，我们需要一个辅助数组 \(F\)，其实就是 \(\text{popcount}\)。可以预处理出来，用于快速维护某一行对应的二进制状态填入了多少个 \(1\)。按题意的描述方式的话，就是在某一行一个合法放置国王的方案中，快速求出该行放置了多少个国王。假设状态为 \(cnt\)，该行放置了 \(sum\) 个国王，那么有 \(F_{cnt} = sum\)

接下来说初始化——直接对第一行进行预处理。由于第一行没有其它行给它的约束，所以只要行内状态合法，就满足条件。形式化地，对于所有合法的状态 \(i\)，有 \(f_{1,i,F_i}=1\)

转移比较显然。第一层循环枚举行，第二、三层循环枚举相邻两行的状态。注意：这里需判断行与行之间是否能满足互不侵犯的条件，出现下列情况的显然不合法：

inline bool check(int k1,int k2){
	return (p[k1]&p[k2])||((p[k1]<<1)&p[k2])||(p[k1]&(p[k2]<<1));
}

第四层枚举国王个数，把所有合法的状态直接转移过来即可

最后统计一下所有合法状态 \(i\) 的 \(f_{n,i,k}\) 的和即可，时间复杂度 \(O(能过)\)

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=10,maxk=85;
int n,k;
int p[1<<maxn],cnt,F[1<<maxn];
int f[maxn][1<<maxn][maxk];
inline void dfs(int pos,int k,int sum){
	if(pos>=n){
		p[++cnt]=k;
		F[cnt]=sum;
		return;
	}
	dfs(pos+1,k,sum);
	dfs(pos+2,k+(1<<pos),sum+1);
	return;
}
inline bool check(int k1,int k2){
	return (p[k1]&p[k2])||((p[k1]<<1)&p[k2])||(p[k1]&(p[k2]<<1));
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>k;
	dfs(0,0,0);
	for(int i=1;i<=cnt;i++){
		f[1][i][F[i]]=1;
	}
	for(int i=2;i<=n;i++){
		for(int k1=1;k1<=cnt;k1++){
			for(int k2=1;k2<=cnt;k2++){
				if(check(k1,k2)){
					continue;
				}
				for(int o=k;o>=F[k1];o--){
					f[i][k1][o]+=f[i-1][k2][o-F[k1]];
				}
			}
		}
	}
	int ans=0;
	for(int i=1;i<=cnt;i++){
		ans+=f[n][i][k];
	}
	cout<<ans<<endl;
	return 0;
}

T11 PRZ（P5911）

链接

状压 DP 经典操作之枚举子集（如果你会枚举子集，这道题你可以直接秒捏！）

先说一下贪心的假做法，因为过桥时间总是和最慢的人的过桥时间绑定在一块。所以有一个假的贪心结论，即以时间为第一关键字（从大到小），重量为第二关键字（从大到小）排序后，能一起走的一起走

这玩意听起来就好假，似乎 luogu 题解区给了个 hack，云落贴这里咯！

Input:

10 4
20 8
15 9
10 1
5 2

Output:

35

所以，干脆就写个 DP，还是状压 DP（数据范围小真的可以为所欲为）。对于某一个状态，不论他是不是一个合法的同时过桥的方案，我们计算其过桥时间、总重量。什么是状态，就是某一个人 是/否 过桥

我们记 \(f_i\) 表示状态 \(i\) 所表示的过桥的人构成的集合可以过桥所花费的最小时间，此时我们要求给出的方案必须合法，即不存在任何一次过桥操作超过桥的限重

转移方程是好写的，形如：

\[f_i = \min_{j \subseteq i} \lbrace T_j + f_{i \oplus j} \rbrace \]

这玩意就是一个简单的枚举子集，时间复杂度 \(O(2^n + 3^n)\)

需要注意的是赋初值为 \(+ \infty\)，不合法的方案直接跳过转移即可

点击查看代码

#include<iostream>
using namespace std;
const int maxn=17,inf=2147483647;
int W,n,t[maxn],w[maxn];
int T[1<<maxn],C[1<<maxn],f[1<<maxn];
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>W>>n;
    for(int i=1;i<=n;i++){
        cin>>t[i]>>w[i];
    }
    for(int i=0;i<(1<<n);i++){
        int b=i,cnt=0;
        while(b){
            cnt++;
            if(b&1){
                C[i]+=w[cnt];
                T[i]=max(T[i],t[cnt]);
            }
            b>>=1;
        }
    }
    for(int i=0;i<(1<<n);i++){
        f[i]=inf;
    }
    f[0]=0;
    for(int i=0;i<(1<<n);i++){
        for(int j=i;j>=0;j=(i&(j-1))){
            if(C[i^j]<=W){
                f[i]=min(f[i],f[j]+T[i^j]);
            }
            if(j==0){
                break;
            }
        }
    }
    cout<<f[(1<<n)-1]<<endl;
    return 0;
}

T12 炮兵阵地（P2704）

链接

~~不愧是某官方组织出的国赛题，终将臭名昭著~~

如果互不侵犯那道题目理解的非常透彻，这道题目也就是小 case 咯！

还是考虑按行转移，首先保证行内方案合法（经过云落的不准确计算，行内合法的状态数至多只有 \(60\) 种）。注意到新一行的炮兵安排方案是受前两行影响的，所以在状态设计的时候需要维护两行的状态

具体地，记 \(f_{i,j,k}\) 表示考虑到第 \(i\) 行，第 \(i\) 行的状态是 \(j\)，第 \(i-1\) 行的状态是 \(k\)，初始化第一行和第二行（需要注意的是，第二行的计算需要依赖于第一行的状态，所以不能同时初始化），考虑转移捏

其实就是依据题意去判断当前的状态是否合法即可，可能条件麻烦点，但是很好想哈！状态转移之前需要标记某一行山地平原的限制，也可以直接把地图状压来做

当你写完状压 DP 愉快地提交之后，你会得到这个东西——

下载数据之后，看着 \(n=1\)，陷入了沉思

所以对于 \(n=1\) 的情况，特判暴搜就行咯！

（P.S. 云落的代码不怎么压行，但是又不打空格，所以码风很抽象，凑合看哈！）

一次函数代码——展示！

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=105,maxm=15,maxs=65;
const int d[]={1,2,-1,-2};
int n,m,cnt;
int K[maxn],f[maxn][maxs][maxs],p[maxs],F[maxs];
bool mp[maxn][maxm];
int col[maxm],ans;
inline bool inbound(int x){
	return x>=1&&x<=m;
}
inline bool check(){
	for(int i=1;i<=m;i++){
		if(col[i]==1&&mp[1][i]){
			return false;
		}
	}
	for(int i=1;i<=m;i++){
		if(col[i]==0){
			continue;
		}
		for(int j=0;j<4;j++){
			int x=i+d[j];
			if(inbound(x)){
				if(col[x]==1){
					return false;
				}
			}
		}
	}
	return true;
}
inline int cal(){
	int res=0;
	for(int i=1;i<=m;i++){
		if(col[i]==1){
			res+=col[i];
		}
	}
	return res;
}
inline void dfs(int cnt){
	if(cnt==m+1){
		if(check()){
			ans=max(ans,cal());
		}
		return;
	}
	col[cnt]=0;
	dfs(cnt+1);
	col[cnt]=1;
	dfs(cnt+1);
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			char c;
			cin>>c; 
			if(c=='H'){
				mp[i][j]=1;
			}
		}
	}
	if(n==1){
		dfs(1);
		cout<<ans<<endl;
		return 0;
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			K[i]=(K[i]<<1)+mp[i][j];
		}
	}
	p[++cnt]=0;
	for(int i=1;i<(1<<m);i++){
		if((i&(i<<1))||(i&(i<<2))||(i&(i>>1))||(i&(i>>2))){
			continue;
		}
		p[++cnt]=i;
		int x=i;
		while(x){
			F[cnt]++;
			x-=(x&(-x));
		}
	}
	for(int i=1;i<=cnt;i++){
		if((p[i]&K[1])==0){
			f[1][i][0]=F[i];
		}
	}
	for(int i=1;i<=cnt;i++){
		if((p[i]&K[2])==0){
			for(int j=1;j<=cnt;j++){
				if((p[i]&p[j])==0&&(p[j]&K[1])==0){
					f[2][i][j]=F[j]+F[i];
				}
			}
		}
	}
	for(int i=3;i<=n;i++){
		for(int j=1;j<=cnt;j++){
			if((p[j]&K[i])==0){
				for(int k1=1;k1<=cnt;k1++){
					if((p[j]&p[k1])==0&&(p[k1]&K[i-1])==0){
						for(int k2=1;k2<=cnt;k2++){
							if((p[j]&p[k2])==0&&(p[k1]&p[k2])==0&&(p[k2]&K[i-2])==0){
								f[i][j][k1]=max(f[i][j][k1],f[i-1][k1][k2]+F[j]);
							}
						}
					}
				}
			}
		}
	}
	int ans=0;
	for(int i=1;i<=cnt;i++){
		for(int j=1;j<=cnt;j++){
			ans=max(ans,f[n][i][j]);
		}
	}
	cout<<ans<<endl;
	return 0; 
}

T13 花园（P1357）

链接

比较抽象的一道题目，语文不好的云落一开始读题都读了好几遍……

由题意可知，一个合法的花园的构造是与 \(m\) 有关的。进一步地，是对每一个区间 \([i,m+i]\) 有关。观察数据范围，\(m \le \min (n,5)\)，我们大可以考虑直接把某一段长度为 \(m\) 的连续区间所有摆放花圃的情况枚举出来，并状态压缩至一个二进制整数中

抛开上述由已知条件入手的正向分析，可以考虑一部分逆向分析（演绎推理与归纳综合……）。可以猜测一下答案的计算方式，计数问题，并且在试填花圃的过程中前后约束紧密，显然不是组合数学的范畴，考虑 DP，结合上文的状态压缩，显然是一道状压 DP

那么，比较自然地设计状态（倍长序列，破环为链的老套路就不说了哈！），记 \(f_{i,j}\) 表示考虑到第 \(i\) 个数，后 \(m\) 位状态为 \(j\) 的方案数

继续往下走，其实我们大概可以写出一个转移方程式，形如：

\[f_{i,j} \gets f_{i-1,j>>1}+f_{i-1,j>>1}|(1<<m-1) \]

其实上述转移式的第二项有一些什么乱七八糟的边界条件的限制，云落偷个懒，不敲了……云落更想说的是状态条件的判断，毕竟还有一个 \(\le k\) 的限制摆在那里。所以建议先把所有合法的状态预处理出来，然后 \(O(1)\) 比对即可

这里说一下手写 popcount 函数，如果各位树状数组学得很好，那么自然会知道 lowbit 的妙用，提示到这里就足够了，嘻嘻

圆规正传，其实上面这个式子正确性很有保障，就是时间复杂度没有一点保障（吐槽：谁家好人 \(n \le 10^{15}\) 啊！？）。但是，注意力惊人的云落发现，一个状态的决策来源非常的稀少，并且我们可以预处理，也就是说，可以尝试用矩阵刻画整个转移。事实上，最后也是可以弄出来的，矩阵快速幂一下就完结撒花了

讲的不是很清楚……建议结合代码食用

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=35,mod=1e9+7;
int n,m,k,N;
struct Matrix{
    int n,m,a[maxn][maxn];
    friend Matrix operator * (Matrix A,Matrix B){
        Matrix C;
        C.n=A.n;
        C.m=B.m;
        memset(C.a,0,sizeof(C.a));
        for(int i=0;i<C.n;i++){
            for(int j=0;j<C.m;j++){
                for(int k=0;k<A.m;k++){
                    C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j]%mod)%mod;
                }
            }
        }
        return C;
    }
}s,res;
Matrix qpow(Matrix A,int b){
    Matrix P;
    P.n=A.n;
    P.m=A.m;
    memset(P.a,0,sizeof(P.a));
    for(int i=0;i<P.n;i++){
        P.a[i][i]=1ll;
    }
    while(b){
        if(b&1){
            P=P*A;
        }
        A=A*A;
        b>>=1;
    }
    return P;
}
inline int lowbit(int x){
	return x&(-x);
}
inline int cal(int x){
	int res=0ll;
	while(x){
		res++;
		x-=lowbit(x);
	}
	return res;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>m>>k;
	N=(1ll<<m);
	s.m=N;
	s.n=N;
	for(int i=0;i<N;i++){
		if(cal(i)<=k){
			int p=i>>1;
			s.a[p][i]=1ll;
			p|=(1ll<<(m-1));
			if(cal(p)<=k){
				s.a[p][i]=1ll;
			}
		}
	}
	res=qpow(s,n);
	int ans=0ll;
	for(int i=0;i<N;i++){
		if(cal(i)<=k){
			ans=(ans+res.a[i][i])%mod;
		}
	}
	cout<<ans<<endl;
	return 0;
}

T14 解锁屏幕（P4460）

链接

大毒瘤：论 \(10^8+7\)、斜率 \(k\)、“两个点之间的连线不能“跨过”另一个点，除非那个点之前已经被‘使用’过”……

日常分析题目，又是一道堂堂唐唐计数题，并且 \(n \le 20\)，非常适合用于枚举哪些点被使用，进一步地，考虑状态压缩

记 \(f_{i,j}\) 表示当前划过的点构成的点集为 \(i\)，且最后一个经过的点的编号为 \(j\)

考虑转移

终于等到这样的一道状压题目咯！是这样滴，状压 DP 是刷表法转移的高发地区，常用于各种奇葩的状压 DP，究其原因就是如果采用填表法，枚举集合的操作可能会在某些情况下并不好做。所以，我们不考虑哪一个状态贡献给了 \(f_{i,j}\)，而考虑 \(f_{i,j}\) 能贡献给哪些状态。上面这种把自己的贡献转移出去的操作叫做刷表法，另外一种叫做填表法

那么这个时候考虑枚举一个新结点 \(k\)，如果结点 \(j\) 向结点 \(k\) 的连线是合法的，那么直接贡献即可，方程大概就是这样——

\[f_{i,j} \to f_{i|(1<<k),k} \]

然后就是这道题目毒瘤的地方了——我们该如何判定一次 \(j\) 向 \(k\) 的拓展是否合法捏？诶嘿，预处理两点之间的斜率关系——也许应该加个定语，在已知选中点集的情况下，判断斜率问题

一些细节：

排序
\(\bmod 10^8+7\)
eps 与 double 的爱恨情仇
popcount \(\ge 4\)

点击查看代码

#include<bits/stdc++.h>
#define x1 x_1
#define y1 y_1
#define x2 x_2
#define y2 y_2
#define int long long
using namespace std;
const int maxn=23,mod=1e8+7;
const double eps=1e-6,inf=2e9;
int n;
struct node{
	int x,y;
	bool operator < (node s){
		if(x!=s.x){
			return x<s.x;
		}
		return y<s.y;
	}
}p[maxn];
int f[1<<maxn][maxn],ans;
int g[maxn][maxn];
inline double K(int x1,int y1,int x2,int y2){
    if(x1==x2){
        return inf;
    }
    return 1.0*(y1-y2)/(x1-x2);
}
inline int lowbit(int x){
	return x&(-x);
}
inline int cal(int x){
    int res=0;
    while(x){
        res++;
		x-=lowbit(x);
    }
    return res;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		int x,y;
		cin>>x>>y;
		p[i]={x,y};
	}
	sort(p+1,p+n+1);
	for(int i=1;i<=n;i++){
		for(int j=i+1;j<=n;j++){
			for(int k=i+1;k<=j-1;k++){
				int xi=p[i].x,yi=p[i].y;
				int xj=p[j].x,yj=p[j].y;
				int xk=p[k].x,yk=p[k].y;
				if(abs(K(xi,yi,xk,yk)-K(xk,yk,xj,yj))<eps){
					g[i][j]|=(1<<k);
					g[j][i]|=(1<<k);
				}
			}
		}
	}
	for(int i=1;i<=n;i++){
		f[1<<i][i]=1;
	}
	for(int i=0;i<(1<<(n+1));i++){
		for(int j=1;j<=n;j++){
			if(i&(1<<j)){
				for(int k=1;k<=n;k++){
					if((i&(1<<k))==0&&k!=j&&(i&g[j][k])==g[j][k]){
						f[i|(1<<k)][k]=(f[i|(1<<k)][k]+f[i][j])%mod;
					}
				}
			}
		}
	}
    for(int i=0;i<(1<<(n+1));i++){
        if(cal(i)>=4){
            for(int j=1;j<=n;j++){
                if(i&(1<<j)){
                    ans=(ans+f[i][j])%mod;
                }
            }
        }
    }
    cout<<ans<<endl;
	return 0;
}

T15 No will to break（P8504）

链接

不会捏，求野生神犇路过浇浇

T16 寿司晚宴（P2150）

链接

2015 年国赛题，不是很热乎咯！

一句话题意：求从 \([2,n]\) 挑出一部分数分成两个集合 \(A,B\)，满足 \(x \in A,y \in B\) 中不存在 \(\text{gcd}(x,y) \neq 1\) 的二元组 \((x,y)\) 的集合 \((A,B)\) 划分方案数

不存在不互质的二元组 \((x,y)\) 可以转化为两个集合中所有的数的质因数构成的集合的交集为空集。显然，\(30 pts\) 的做法呼之欲出，状压所有可能的质因数，记 \(dp_{S_1,S_2}\) 表示集合划分后的答案，简单刷表转移即可

但是现在 \(n \le 500\)，这个范围内质数足足有 \(95\) 个！很明显上面这种偏暴力的状压没有任何前途……

于是乎我们继续观察性质，发现 \(23^2 = 529\)，也就是说，一个 \([2,500]\) 范围内的数最多只能分解出一个 \(\ge 23\) 的质因数。进一步地，是不是可以考虑不同情况差别对待捏？答案是可以的。索性，我们干脆维护三个东西，用于统计小质因数方案划分之后的所有情况，大质因数划归集合 \(B\) 的所有情况，大质因数划归集合 \(A\) 的所有情况，分别记为 \(dp_{A,B},dp1_{A,B},dp2_{A,B}\)

转移开始之前，需要对每个数进行质因数分解，小质因数的部分直接状压至 \(8\) 位二进制数 \(S\) 里，大质因数拉出来记在 \(v\) 里，然后按 \(v\) 从小到大排序。显然有前面一段 \(v=0\) 的，和后面一段 \(v\) 为某个大质因数的。相同 \(v\) 的数要一起处理捏！

是——转移时间

首先，\(dp_{0,0}=1\)。然后在每一次 \(v\) 更换（或 \(v=0\)）的时候要把 \(dp\) 数组直接拷贝给 \(dp1,dp2\)

在相同的 \(v\) 内，我们对 \(dp1,dp2\) 进行更新，刷表法比较好用捏。每进来一个新的 \(S\)，就直接分类讨论，分配给 \(dp1,dp2\)

当 \(v\) 相同的一段已经全部统计完毕之后，\(dp\) 要合并 \(dp1,dp2\) 两个东西的答案，但是——按下面式子转移会假

\[dp_{A,B} = dp1_{A,B} + dp2_{A,B} \]

我请问哈，如果我大质因数一个都不要，是不是算重了？所以正确的转移方式是这样滴！

\[{dp'}_{A,B} = dp1_{A,B} + dp2_{A,B} - dp_{A,B} \]

别忘了取模就行，对于所有合法的 \((A,B)\)，直接统计 \(dp_{A,B}\) 的和即可

（思路及代码实现参考 luogu 题解区第二篇）

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=512,maxp=8;
const int prime[]={2,3,5,7,11,13,17,19};
int n,p;
struct node{
	int S,v;
	bool operator < (node x){
		return v<x.v;
	}
}s[maxn];
int dp[maxn][maxn],dp1[maxn][maxn],dp2[maxn][maxn];
inline void init(int x){
	int tmp=x;
	for(int i=0;i<maxp;i++){
		if(tmp%prime[i]==0){
			s[x].S|=(1<<i);
			while(tmp%prime[i]==0ll){
				tmp/=prime[i];
			}
		}
	}
	if(tmp>1ll){
		s[x].v=tmp;
	}
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>p;
	for(int i=2;i<=n;i++){
		init(i);
	}
	sort(s+2,s+n+1);
	dp[0][0]=1;
	int state=(1<<maxp)-1;
	for(int i=2;i<=n;i++){
		if(s[i].v!=s[i-1].v||s[i].v==0){
			memcpy(dp1,dp,sizeof(dp));
			memcpy(dp2,dp,sizeof(dp));
		}
		for(int A=state;A>=0;A--){
			for(int B=state;B>=0;B--){
				if(A&B){
					continue;
				}
				if((s[i].S&A)==0){
					dp1[A][B|s[i].S]=(dp1[A][B|s[i].S]+dp1[A][B])%p;
				}
				if((s[i].S&B)==0){
					dp2[A|s[i].S][B]=(dp2[A|s[i].S][B]+dp2[A][B])%p;
				}
			}
		}
		if(i==n||s[i].v!=s[i+1].v||s[i].v==0){
			for(int A=0;A<=state;A++){
				for(int B=0;B<=state;B++){
					if(A&B){
						continue;
					}
					dp[A][B]=(dp1[A][B]+dp2[A][B]-dp[A][B]+p)%p;
				}
			}
		}
	}
	int ans=0ll;
	for(int A=0;A<=state;A++){
		for(int B=0;B<=state;B++){
			if(A&B){
				continue;
			}
			ans=(ans+dp[A][B])%p;
		}
	}
	cout<<ans<<endl;
	return 0;
}

后记

是梦，总会醒的……

完结撒花！

posted @ 2025-03-06 12:58 sunxuhetai 阅读(19) 评论(0) 收藏举报

刷新页面返回顶部

浮海沉天

笔名：云落

1.12 下午-换根 DP & 数位 DP & 状压 DP

前言

正文

知识点

一题一解

T1 STA-Station（P3478）

T2 Nearby Cows G（P3047）

T3 连珠线（P3647）

观察性质

DP！

细节与代码实现

T4 建造军营（P8867）

T5 Minimax（P5298）

T6 windy 数（P2657）

T7 数字计数（P2602）

T8 花神的数论题（P4317）

T9 Sam 数（P2106）

T10 互不侵犯（P1896）

T11 PRZ（P5911）

T12 炮兵阵地（P2704）

T13 花园（P1357）

T14 解锁屏幕（P4460）

T15 No will to break（P8504）

T16 寿司晚宴（P2150）

后记

公告