最优控制学习笔记3----无约束条件的泛函极值问题

无约束条件的最优控制问题

设函数 \(x(t)\) 在 \([t_0, t_f]\) 区间上连续可到，考虑 Lagrange型性能指标函数 \(J[x(t)]=\displaystyle\int_{t_0}^{t_f}L[x(t), \dot{x}(t), t]dt\)

终端时刻确定的性能指标变分

此时终端时刻 \(t_f\) 是一个确定的数，积分型的性能指标相当于是一个确定上下限的定积分。设宗量函数 \(x(t)\), \(\dot{x}(t)\) 在极值曲线 \(x^*(t)\), \(\dot{x}^*(t)\) 附近发生微小变分 \(\delta \eta(t)\), \(\delta \dot{\eta}(t)\), 其中 \(\eta(t)\) 是一个连续可导的任意定义区间内的函数，即

\[x(t)=x^*(t)+\delta \eta(t),\tag{1} \]

\[\dot{x}(t)=\dot{x}^*(t)+\delta \dot{\eta}(t),\tag{2} \]

则泛函 \(J[x(t)]\) 的增量 \(\Delta J[x(t)]\) 可表示为

\[\begin{aligned} \Delta J[x(t)]&=\displaystyle\int_{t_0}^{t_f}\{L[x(t), \dot{x}(t),t]-L[x^*(t), \dot{x}^*(t),t]\}dt\\ &=\displaystyle\int_{t_0}^{t_f}\{\frac{\partial L}{\partial x}\delta \eta+\frac{\partial L}{\partial \dot{x}}\delta \dot{\eta}+o[(\delta \eta)^2, (\delta \dot{\eta})^2]\}dt \end{aligned} \]

其中

\[\begin{aligned} \displaystyle\int_{t_0}^{t_f}\frac{\partial L}{\partial \dot{x}}\delta \dot{\eta}dt=\frac{\partial L}{\partial \dot{x}}\delta \eta|_{t_0}^{t_f}-\displaystyle\int_{t_0}^{t_f}\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})\delta \eta dt \end{aligned},\]

所以

\[\delta J=\displaystyle\int_{t_0}^{t_f}(\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}}))\delta \eta dt+\frac{\partial L}{\partial \dot{x}}\delta \eta|_{t_0}^{t_f}.\tag{3} \]

由泛函极值的必要条件可得，若泛函\(J[x(t)]\) 取得极值，则有\(\delta J=0\), 根据（3）式，若要\(\delta J=0\)，则有

\[\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})=0,\tag{4} \]

以及

\[\frac{\partial L}{\partial \dot{x}}\delta \eta|_{t_0}^{t_f}=0,\tag{5} \]

上式公式 (4) 称为欧拉-拉格朗日方程, 公式(5)被称为横截条件。
始端，终端状态的固定与否对公式(4)无影响，但会影响公式(5)的具体表达形式，以下分如下四种情况分析模型的边界条件。

1. 始端状态，终端状态固定

此时初始状态 \(x(t_0)=x_0\), \(x(t_f)=x_f\)。则\(\eta(t)|_{t_0}^{t_f}=0\)。则求解时应用给定的边界条件即可，无须横截条件。

2. 始端状态给定，终端状态自由

此时初始状态 \(x(t_0)=x_0\)，\(\eta(t_0)=0\). 由\(\eta(t)\) 的任意性, 此时需要 \(\frac{\partial L}{\partial \dot{x}}|_{t_f}=0\)。

3. 始端状态自由，终端状态给定

此时终端状态 \(x(t_f)=x_f\)，\(\eta(t_f)=0\). 由\(\eta(t)\) 的任意性, 需要 \(\frac{\partial L}{\partial \dot{x}}|_{t_0}=0\)。

4. 始端状态自由，终端状态自由

此时对于任意的\(\eta(t)\), 在\(t_0\), \(t_f\)两点的取值不定，由\(\eta(t)\) 的任意性, 需要 \(\frac{\partial L}{\partial \dot{x}}|_{t_0}=0\)，\(\frac{\partial L}{\partial \dot{x}}|_{t_f}=0\)

总结：求解无约束条件的泛函极值问题时，若给定了边界条件，则直接应用边界条件，若始端或终端状态的条件未给出，则需要使用始端或终端的横截条件进行求解。求解条件如下表所示：

	边界条件	满足方程：欧拉-拉格朗日方程
始端固定，终端固定	\(x(t_0)=x_0, x(t_f)=x_{t_f}\)	\(\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})=0\)
始端固定，终端自由	\(x(t_0)=x_0,\frac{\partial L}{\partial \dot{x}}|_{t_f}=0\)	\(\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})=0\)
始端自由，终端固定	\(\frac{\partial L}{\partial \dot{x}}|_{t_0}=0, x(t_f)=x_f\)	\(\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})=0\)
始端自由，终端自由	\(\frac{\partial L}{\partial \dot{x}}|_{t_0}=0,\frac{\partial L}{\partial \dot{x}}|_{t_f}=0\)	\(\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})=0\)

例题

• 初始与终端状态固定
  求通过点 \((0,0)\), \((1,1)\) 且使

\[J=\displaystyle \int_0^1(x^2+\dot{x}^2)dt \]

取极值的最优轨迹。
解：此处 \(L(x(t), \dot{x}(t), t)=x^2+\dot{x}^2\), 性能指标函数相应的欧拉-拉格朗日方程为

\[\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})=0. \]

则有

\[2x-2\frac{d}{dt}(\dot{x})=0, \]

即

\[x-\ddot{x}=0. \]

故求得基解为 \(e^t\), \(e^{-t}\), 则最优轨迹的通解可表示为

\[x(t)=c_1e^t+c_2e^{-t},\tag{10} \]

其中 \(c_1\) 和 \(c_2\) 都为常数。
将初始条件 \(x(0)=0\) 与终端条件 \(x(1)=1\) 代入方程 (10) 可得：

\[c_1=\frac{1}{e-e^{-1}},c_2=\frac{1}{e^{-1}-e}, \]

故而最优轨迹为

\[x(t)=\frac{e^t-e^{-t}}{e-e^{-1}}. \]

• 终端状态不固定
  求使得性能指标

\[J=\displaystyle \int_0^1(\dot{x}^2+\dot{x}^3)dt \]

取极值的轨迹 \(x^*(t)\), 并要求 \(x^*(0)=0\), 但对 \(x^*(1)\) 没有限制。
解： 此处始端状态给定，终端状态未给定，所以需要用到始端状态相关的边界条件，终端状态相关的横截条件。这里 \(L(x(t), \dot{x}(t), t)=\dot{x}^2+\dot{x}^3\)，该性质指标函数对应的欧拉-拉格朗日函数为

\[-\frac{d}{dt}(2\dot{x}+3\dot{x}^2)=0,\tag{11} \]

以及横截条件

\[(2\dot{x}+3\dot{x}^2)_{t=1}=0.\tag{12} \]

由方程 (11) 可知，\(2\dot{x}+3\dot{x}^2=常数\)，则可知 \(x^*(t)\) 为关于 \(t\) 的一次函数，设 \(x^*(t)=at+b\), 则由 \(x^*(0)=0\) 可知 \(b=0\)。由方程(12)可知 $$2a+3a^2=0,\tag{13}$$
解得 \(a=0\) 或 \(a=-\frac{2}{3}\)，所以最优轨迹 \(x^*(t)\) 可表示为：
(i) 若 \(a=0\)，则 \(x^*(t)=0\);
(ii) 若 \(a=-\frac{2}{3}\)，则 \(x^*(t)=-\frac{2}{3}t\).

终端时刻不确定的性能指标变分

此时性能指标函数 \(J[x(t)]=\displaystyle\int_{t_0}^{t_f}L[x(t), \dot{x}(t), t]dt\) 类似于一个变上限的积分函数。
类似于终端时刻确定时，设宗量函数 \(x(t)\), \(\dot{x}(t)\) 在极值曲线 \(x^*(t)\), \(\dot{x}^*(t)\) 附近发生微小变分 \(\delta \eta(t)\), \(\delta \dot{\eta}(t)\), 其中 \(\eta(t)\) 是一个连续可导的任意定义区间内的函数，即

\[x(t)=x^*(t)+\delta \eta(t),\tag{14} \]

\[\dot{x}(t)=\dot{x}^*(t)+\delta \dot{\eta}(t),\tag{15} \]

取得状态 \(x^*\) 的时刻为 \(t_f^*\), 状态 \(x(t)\) 对应 时刻 \(t_f\), 设 \(t_f=t_f^*+\delta\xi(t_f^*)\)
则泛函 \(J[x(t)]\) 的增量 \(\Delta J[x^*(t)]\) 可表示为

\[\begin{aligned} \Delta J[x^*(t)]&=\frac{\partial J}{\partial \delta}|_{\delta=0}\\ &=\displaystyle\int_{t_0}^{t_f^*}\{L[x(t), \dot{x}(t),t]-L[x^*(t), \dot{x}^*(t),t]\}dt+L[x^*(t_f^*), \dot{x}^*(t_f^*),t_f^*]\xi(t_f^*)\\ &=\displaystyle\int_{t_0}^{t_f^*}\{\frac{\partial L}{\partial x}\delta \eta+\frac{\partial L}{\partial \dot{x}}\delta \dot{\eta}+o[(\delta \eta)^2, (\delta \dot{\eta})^2]\}dt+L[x^*(t_f^*), \dot{x}^*(t_f^*),t_f^*]\xi(t_f^*) \end{aligned} \]

其中

\[\begin{aligned} \displaystyle\int_{t_0}^{t_f^*}\frac{\partial L}{\partial \dot{x}}\delta \dot{\eta}dt=\frac{\partial L}{\partial \dot{x}}\delta \eta|_{t_0}^{t_f^*}-\displaystyle\int_{t_0}^{t_f^*}\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})\delta \eta dt \end{aligned}.\]

因此 \(\delta J\) 取得极值的必要条件为：
（1）欧拉-拉格朗日方程：

\[\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})=0, \]

(2) 横截条件：

\[\eta(t)\frac{\partial L}{\partial \dot{x}}|_{t_0}^{t_f^*}+L[x^*(t_f^*), \dot{x}^*(t_f^*),t_f^*]\xi(t_f^*)=0. \]

通常，无论边界情况如何，泛函极值都必须满足欧拉-拉格朗日方程，只是在不同的情况下会出现不同的边界情况，以下我们分情况进行讨论。

1. 给定始端状态与终端状态
   
   此时 \(x(t_0)=x_0\), \(\eta(t_0)=0\), \(\eta(t_f^*)=0\), \(x(t_f)=x_f\), 则可得边界条件与横截条件为

\[x(t_0)=x_0, x(t_f)=x_f, L[x(t_f^*), \dot{x}(t_f^*), t_f^*]=0. \]

2. 始端状态给定，终端状态自由
   此时 \(x(t_0)=x_0\), \(\eta(t_0)=0\), \(\eta(t_f^*)\neq0\), 则可得边界条件与横截条件为

\[x(t_0)=x_0, \frac{\partial L}{\partial \dot{x}}|_{t_f^*}=0, L[x(t_f^*), \dot{x}(t_f^*), t_f^*]=0. \]

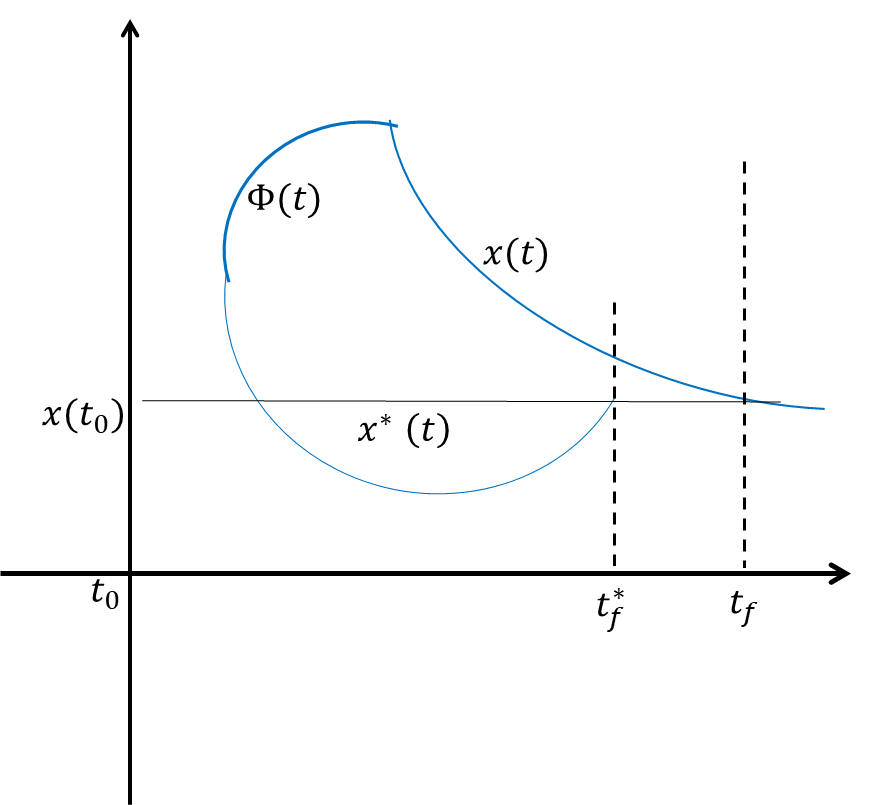
3. 始端状态给定，终端状态有约束（要求 \(x(t_f)=C(t_f)\)）
   
   \(x(t)=x^*(t)+\varepsilon\eta(t)\), \(t_f=t_f^*+\varepsilon\xi(t_f^*)\)
   则有

\[\begin{aligned} C(t_f)&=x(t_f)\\ &=x^*(t_f)+\varepsilon\eta(t_f)\\ &=x(t_f^*+\varepsilon\xi(t_f^*))\\ &=x^*(t_f^*+\varepsilon\xi(t_f^*))+\varepsilon\eta(t_f^*+\varepsilon\xi(t_f^*))\\ &=C(t_f^*+\varepsilon\xi(t_f^*))\\ \end{aligned} \]

上式在 \(\varepsilon=0\) 处取求导可得

\[\begin{aligned} &\eta(t_f^*+\varepsilon\xi(t_f^*))|_{\varepsilon=0}\\ &=\frac{C(t_f^*+\varepsilon\xi(t_f^*))-x^*(t_f^*+\varepsilon\xi(t_f^*))}{\varepsilon}|_{\varepsilon=0}\\ &=(\dot{C}(t_f^*)-\dot{x}^*(t_f^*))\xi(t_f^*)\\ &=\eta(t_f^*) \end{aligned} \]

则可得边界条件与横截条件为

\[\begin{cases} x(t_0)=x_0,\\ x(t_f)=C(t_f),\\ (\dot{C}(t_f^*)-\dot{x}^*(t_f^*))\frac{\partial L}{\partial \dot{x}}|_{t_f^*}+L[x^*(t_f^*), \dot{x}^*(t_f^*),t_f^*]=0.\\ \end{cases} \]

4. 始端状态有约束（要求 \(x(t_0)=\Phi(t_0)\)），终端状态固定
   

\(x(t)=x^*(t)+\varepsilon\eta(t)\), \(t_0=t_0^*+\varepsilon\xi(t_0^*)\)
则有

\[\begin{aligned} \Phi(t_0)&=x(t_0)\\ &=x^*(t_0)+\varepsilon\eta(t_0)\\ &=x(t_0^*+\varepsilon\xi(t_0^*))\\ &=x^*(t_0^*+\varepsilon\xi(t_0^*))+\varepsilon\eta(t_0^*+\varepsilon\xi(t_0^*))\\ &=C(t_0^*+\varepsilon\xi(t_0^*))\\ \end{aligned} \]

上式在 \(\varepsilon=0\) 处取求导可得

\[\begin{aligned} &\eta(t_0^*+\varepsilon\xi(t_0^*))|_{\varepsilon=0}\\ &=\frac{C(t_0^*+\varepsilon\xi(t_0^*))-x^*(t_0^*+\varepsilon\xi(t_0^*))}{\varepsilon}|_{\varepsilon=0}\\ &=(\dot{C}(t_0^*)-\dot{x}^*(t_0^*))\xi(t_0^*)\\ &=\eta(t_0^*) \end{aligned} \]

则可得边界条件与横截条件为

\[\begin{cases} x(t_f)=x_f,\\ x(t_0)=\Phi(t_f),\\ (\dot{\Phi}(t_0^*)-\dot{x}^*(t_0^*))\frac{\partial L}{\partial \dot{x}}|_{t_0^*}+L[x^*(t_0^*), \dot{x}^*(t_0^*),t_0^*]=0.\\ \end{cases} \]

总结：在终端时刻不确定的条件下，求解无约束条件的泛函极值问题时，若给定了边界条件，则直接应用边界条件，若始端或终端状态的条件未给出，则需要使用始端或终端的横截条件进行求解。求解条件如下表所示：

	边界条件
给定始端状态与终端状态	\(x(t_0)=x_0, x(t_f)=x_f, L[x(t_f^*), \dot{x}(t_f^*), t_f^*]=0\)
始端状态给定终端状态自由	\(x(t_0)=x_0\),\(\frac{\partial L}{\partial \dot{x}}|_{t_f^*}=0\),\(L[x(t_f^*), \dot{x}(t_f^*), t_f^*]=0\)
始端状态给定，终端状态有约束（要求 \(x(t_f)=C(t_f)\)）	\(x(t_0)=x_0,x(t_f)=C(t_f),(\dot{C}(t_f^*)-\dot{x}^*(t_f^*))\frac{\partial L}{\partial \dot{x}}|_{t_f^*}+L[x^*(t_f^*), \dot{x}^*(t_f^*),t_f^*]=0\)
始端状态有约束（要求 \(x(t_0)=\Phi(t_0)\)），终端状态固定	\(x(t_f)=x_f,x(t_0)=\Phi(t_0),(\dot{\Phi}(t_0^*)-\dot{x}^*(t_0^*))\frac{\partial L}{\partial \dot{x}}|_{t_0^*}+L[x^*(t_0^*), \dot{x}^*(t_0^*),t_0^*]=0.\)

例题

求使性能指标

\[J=\displaystyle \int_{t_0}^{t_f}(1+\dot{x}^2)^{\frac{1}{2}}dt \]

为极小时的最优轨线 \(x^*(t)\)。设 \(x(0)=1, x(t_f)=C(t_f), C(t_f)=2-t\), \(t_f\) 未给定。
解题思路 本题为无约束条件，始端状态时刻给定，终端状态有约束，终端时刻自由的泛函极值问题。
令 \(L(x,\dot{x},t)=(1+\dot{x}^2)^{\frac{1}{2}}\)。则可得欧拉-拉格朗日方程为

\[\frac{\partial L}{\partial x}-\frac{d}{dt}\frac{\partial L}{\partial \dot{x}}=0,\tag{e1} \]

可得

\[-\frac{d}{dt}(\frac{\dot{x}}{(1+\dot{x}^2)^{\frac{1}{2}}})=0,\tag{e2} \]

则有

\[\frac{\dot{x}}{(1+\dot{x}^2)^{\frac{1}{2}}}=c,\tag{e3} \]

得

\[\dot{x}^2=\frac{c^2}{1-c^2}, c^2\neq1.\tag{e4} \]

即 \(\dot{x}\) 为常数，进而可知 \(x(t)\) 为一次函数形式，设

\[x(t)=at+b, \tag{e5} \]

代入初始条件 \(x(0)=1\) 可得 \(b=1\)。由横截条件

\[(\dot{c}(t_f)-\dot{x}(t_f))\frac{\partial L}{\partial \dot{x}}|t_f=t_f^*+L(x(t_f),\dot{x}(t_f),t_f)=0 \]

可得

\[(-1-a)[\frac{a}{(1+a^2)^{\frac{1}{2}}}]+(1+a^2)^{\frac{1}{2}}=0, \]

整理可得

\[a(a-1)(a+2)=0,\tag{e6} \]

由（e6）可知 \(a=0\), 或 \(a=1\) 或 \(a=-1\). 经验算可知 \(a=-1\) 时，不满足终端约束 \(x(t_f)=c(t_f)\),即会有 \(-t_f+1=2-t_f\)。所以\(a=0\), 或 \(a=1\)。
（1）当 \(a=0\) 时，最优轨迹为 \(x(t)=1\), 代入条件 \(x(t_f)=c(t_f)\)，得最优时刻为 \(t_f^*=1\)。
（2）当\(a=1\) 时，最优轨迹为 \(x(t)=t+1\), 代入条件 \(x(t_f)=c(t_f)\)，得最优时刻为 \(t_f^*=\frac{1}{2}\)。