Ds

基础数据结构

单调队列

概述

例题

3354 -- 【牛客网2020day6】艰难睡眠

首先断环为链后，发现 \(m \le 2000\)，启示我们可以枚举时间点。

扫描线后，问题转化对每个时间点求解出 \(n\) 个人不在 \([i,i+k-1]\) 时间段中所最少需要花费的代价，那么也就是总区间减去这个区间后剩余区间的最小值，再因为 \(i \rightarrow i+1\) 是相当于滑动窗口最小值。这个可以用单调队列很轻松的维护。

时间复杂度：\(\mathcal O(nm)\)。

树状数组

概述

例题

P6958 [NEERC 2017] The Great Wall

注意：\(a_{0,i}<a_{1,i}<a_{2,i}\)。

考虑二分答案 \(x\)，转化为统计答案不超过 \(x\) 的方案个数是否至少有 \(k\) 个。

首先可以将 \(a_1\) 和 \(a_2\) 中每个元素都减去 \(a_0\) 对应位置的元素，最后答案加上 \(a_0\) 中所有元素之和，转换成对于两个数组的问题。

\[b_{1,i}=a_{1,i}-a_{0,i},b_{2,i}=a_{2,i}-a_{0,i} \]

1. Case1. \(I \cap J=\varnothing\)

   设两个区间分别为 \(I=[s,s+r-1]\) 和 \(J=[t,t+r-1]\)，则 \(w(I,J)=\sum_{i\in I}b_{1,i}+\sum_{i\in J}b_{1,i}\)。考虑前缀和优化，令 \(pre_i=\sum_{j=1}^i b_{1,j}\)，则 \(w(I,J)=pre_{s+r-1}-pre_{s-1}+pre_{t+r-1}-pre_{t-1}\)。令 \(f_i=pre_{i+r-1}-pre_{i-1}\)，则 \(w(I,J)=f_s+f_t\)。于是需要求出有多少对 \(s,t\)，满足 \(1\le s\le n-2r+1,s+r\le t\le n-r+1,f_s+f_t\le x\)（不妨设 \(J\) 在 \(I\) 右边，去重），显然是一个二维数点问题。

2. Case2. \(I\cap J\ne \varnothing\)

   则 \(w(I,J)=\sum_{i=s}^{t-1} b_{1,i}+\sum_{i=t}^{s+r-1}b_{2,i}+\sum_{i=s+r}^{t+r-1}b_{1,i}\)，令 \(pre'_i=\sum_{j=1}^ib_{2,j},g_i=pre'_{i+r-1}-pre_{i-1}-pre_{i+r-1},h_i=pre_{i-1}-pre'_{i-1}+pre_{i+r-1}\)，则 \(w(I,J)=g_s+h_t\)。于是也是一个二维数点：\(1\le s<n-r+1,s<t\le \min(s+r-1,n-r+1),g_s+h_t\le x\)。

扫描线定一求一降一维，数据结构（BIT维护一维）即可。

具体地，先预处理出 \(f_i,g_i,h_i\) 并把它们排序，然后在二分中可以双指针先根据 \(f_s+f_t\) 的限制求出 \(t\) 固定时所有满足条件的 \(s\)，使 \(f_s+f_t\le mid\)。设这些 \(s\) 组成的集合为 \(S\)。此时转化为了求 \(S\) 中有多少个元素 \(x\) 满足 \(x+r\le t\)，转化为了一个一维偏序问题，用数据结构维护即可。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

此题代码实现及其简单，先放出代码供参考。

struct BIT{
	int tree[N];
	void update(int k,int x){for(;k<=n;k+=lowbit(k))tree[k]+=x;}
	int query(int k){int res=0;for(;k>0;k-=lowbit(k))res+=tree[k];return res;}
	void cle(){memset(tree,0,sizeof(tree));}
}T;
int check(int x)
{
	T.cle();int cnt=0;
	for(int t=n-r+1,s=1;t;t--)
	{
		while(s<=n-r+1&&f[s].fi+f[t].fi<=x)T.update(f[s].sd,1),s++;
		cnt+=T.query(f[t].sd-r);
	}
	T.cle();
	for(int t=n-r+1,s=1;t;t--)
	{
		while(s<=n-r+1&&g[s].fi+h[t].fi<=x)T.update(g[s].sd,1),s++;
		cnt+=T.query(h[t].sd-1)-T.query(h[t].sd-r);
	}
	return cnt;
}
void solve()
{
	cin>>n>>r>>k;
	for(int i=1;i<=n;i++)cin>>a[i],sum+=a[i];
	for(int i=1;i<=n;i++)cin>>b[i],b[i]-=a[i],b[i]+=b[i-1];
	for(int i=1;i<=n;i++)cin>>c[i],c[i]-=a[i],c[i]+=c[i-1];
	for(int i=1;i<=n-r+1;i++)
	{
		f[i]=mk(b[i+r-1]-b[i-1],i);
		g[i]=mk(c[i+r-1]-b[i-1]-b[i+r-1],i);
		h[i]=mk(b[i-1]+b[i+r-1]-c[i-1],i);
	}
	sort(f+1,f+1+n-r+1);sort(g+1,g+1+n-r+1);sort(h+1,h+1+n-r+1);
	int l=0,r=c[n],ans=0;
	while(l<=r)
	{
		if(check(mid)>=k)ans=mid,r=mid-1;
		else l=mid+1;
	}
	cout<<ans+sum<<endl;
}

线段树

线段树的应用

普通应用

CF1436E Complicated Computations

本道题有两种主流做法，线段树和莫队。

Solution 1：线段树

能证明最后答案的区间在 \([1,n+2]\) 之间。

由于求的是所有子区间 \(mex\) 的 \(mex\)，所以我们先考虑一个子区间，满足其 \(mex\) 为 \(x\)。那么我们把所有在原数组中出现过的 \(x\) 的下标记录下来，并把它们从小到大排序，记现在数组为 \(p_1,p_2,\dots,p_m\)，我们我们原来找到的这个子区间必然不能包含任意 \(p_i\)，即只能在 \([p_j+1,p_{j+1}-1]\) 中出现。又因为这个子区间的 \(mex\) 为 \(x\)，则说明 \([1,x-1]\) 都在这个子区间出现过了。

那么我们可以从左往右进行扫描线，记 \(last_i\) 表示 \(i\) 这个数最后出现的位置，没有则为 \(0\)。那么当前的数为 \(a_i\)，如果我们钦定 \(a_i\) 最后作为任意一个子区间的 \(mex\)，那么所有子区间在 \([last_{a_i}+1,i-1]\) 中应该有值在 \([1,a_i-1]\) 中都出现。即 \(\min_{j=1}^{a_i-1} last_j>last_{a_i}\),那么 \(a_i\) 一定作为一个子区间的 \(mex\) 出现。

时间复杂度：\(\mathcal O(n \log n)\)。

Solution 2：莫队

因为 \([last_x+1,x-1]\) 这样的段只有 \(\mathcal O(n)\) 段，所以莫队可以构造出询问每次询问 \([last_x+1,x-1]\) 是否满足 \(\min_{j=1}^{a_x-1} last_j>last_x\)。

如果用树状数组询问 \([1,y]\) 是否都出现的话，复杂度为 \(\mathcal O(n\sqrt{n}\log n)\)。但是我们能接受的是 \(\mathcal O(1)\) 修改，\(\mathcal O(\sqrt{n})\) 询问。所以使用值域分块即可。

时间复杂度：\(\mathcal O(n\sqrt{n})\)。

代码：

const int MAXN = 1e5+10;
int val[MAXN<<2],lst[MAXN],a[MAXN],n;
bool able[MAXN];
//这个线段树维护的是每个数最后出现的位置
void update(int o,int l,int r,int pos,int v){
	if(l == r) return (void)(val[o] = v);
	int mid = l+r>>1;
	if(pos <= mid) update(o<<1,l,mid,pos,v);
	else update(o<<1|1,mid+1,r,pos,v);
	val[o] = min(val[o<<1],val[o<<1|1]);
}//更新区间最小值
int query(int o,int l,int r,int xl,int xr){
	if(l == xl && r == xr) return val[o];
	int mid = l+r>>1;
	if(xr <= mid) return query(o<<1,l,mid,xl,xr);
	else if(xl > mid) return query(o<<1|1,mid+1,r,xl,xr);
	else return min(query(o<<1,l,mid,xl,mid),query(o<<1|1,mid+1,r,mid+1,xr));
}//查询区间最小值
int main (){//lst[i] i 上一次出现的位置
	scanf("%d",&n);
	for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
	for(int i = 1;i <= n;i++){
		if(a[i] != 1) able[1] = 1;//注意对1的特判
		if(a[i] > 1  && query(1,1,n,1,a[i]-1) > lst[a[i]]) able[a[i]] = 1;
      //对段进行分割处理（lst[a[i]] ~ i) ，如果 1~a[i]-1 的数最后出现的位置都 > lst[a[i]] 且 < i(因为后面的还没更新，所以必定 < i) ,那么这一段满足MEX = a[i]
		lst[a[i]] = i;
		update(1,1,n,a[i],i);
	}
	for(int i = 2;i <= n+1;i++) if(query(1,1,n,1,i-1) > lst[i]) able[i] = 1;
  //因为lst[i] 初始为0，所以之前我们处理了 1～i 最先出现的位置的段，但是没有处理 lst[i] ~ 结尾 的段，这里在处理一遍
	int ans = 1;
	for(;able[ans] && ans <= n+1;ans++);
  //查找答案，注意ans 上界实际上为 n+2
	printf("%d\n",ans);
	return 0;
}

P2824 [HEOI2016/TJOI2016] 排序

注意到只有一次询问，所以我们考虑二分最终这个值。

那么我们把所有小于等于 \(x\) 的值赋值为 \(0\)，大于 \(x\) 的值赋值为 \(0\)。

那么在 check 时就可以把 \(01\) 数组排序，这个可以很轻松用线段树维护。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

好题，一种基于01串的神奇的二分思想。

CF558E A Simple Task

非常好的一道题，是线段树的常见玩法。实际上和上一道题差不多。

将字符串转化为 \(1\sim 26\) 个数

对区间开一棵线段树，用两个数组分别维护区间中 \(1\sim 26\) 每个数的个数以及一个区间覆盖标记，表示这个区间是否被某一个值覆盖了。

在每次排序时，首先查出这个区间中 \(1\sim 26\) 每个数出现的次数，然后因为是排过序的，所以相等的数排完序之后一定是连续的一段区间，这样如果升序，我们就对整个区间从小到大进行覆盖，否则从大到小覆盖

最后遍历整棵线段树输出即可

一句话总结：每次排序只需做一次区间查询，\(26\) 次区间覆盖，这样时间复杂度 \(\mathcal O(26n\log n)\)。

P10240 [THUSC 2021] 搬东西

思路分析

首先考虑怎么选出最多元素，显然会按从小到大的顺序贪心取出前 \(k\) 个元素。

然后考虑怎么确定一组解，可以逐位贪心，即先最大化标号最小元素的位置，可以二分一个 \(x\)，那么我们就要求 \([x,n]\) 范围内前 \(k\) 小元素和 \(\le m\)。

由于我们要动态删除元素，因此可以树状数组套值域线段树树，求出一组解的复杂度 \(\mathcal O(k\log^3n)\)。

由于 \(\sum k=n\)，因此总复杂度 \(\mathcal O(n\log ^3n)\)。

从小到大贪心求 \(k\) 可以直接 std::multiset 维护。

时间复杂度：\(\mathcal O(n\log^3n)\)。

搭配单调栈

#6698. 一键挖矿 - 题目 - LibreOJ

Pudding Monster 的加强版，考虑怎么做。

直接套用一维做法做不了，但是有基于 \((\max(x)-\min(x)+1)(\max(y)-\min(y)+1)=r-l+1\) 的分治做法。

这里叙述一下人类智慧做法。

加入权值在区间 \([l,r]\) 内的格子，令它们的颜色为黑色，其它的格子颜色为白色。

考虑所有的 \((n+1)×(m+1)\) 个 \(2×2\) 的小正方形(超出边界也算)，则所有黑色格子形成一个矩形，当且仅当恰好有 \(4\) 个小正方形内部有 \(1\) 个黑色格子，并且没有任何一个小正方形内部有 \(3\) 个黑色格子。

必要性是显然的,任何一个由黑色格子组成的矩形都满足以上条件。充分性可以这样考虑，初始时一定是有 \(4\) 个黑色格子，要求恰好有 \(4\) 个小正方形内部有 \(1\) 个黑色格子，就必须用黑色格子将它们连起来，形成矩形的边界，而此时角的地方会出现包含 \(3\) 个黑色格子的小正方形，只有将内部全部填满后才会消失，于是可以得出这个条件是充分必要的。

有了这个结论，再来考虑如何计算答案。我们从小到大枚举 \(r\) ，并对每个 \(l≤r\) 维护 \(f(l)\) ，表示将权值在 \([l,r]\) 内的格子染黑后，有多少个小正方形内部有 \(1\) 个或 \(3\) 个黑色格子。不难发现 \(f(l)≥4,f(r)=4\) 是恒成立的，根据上面的结论，我们只需要求有多少个 \(f(l)=4\)，即最小值的个数。

用线段树维护 \(f\) 以及最小值个数，每次 \(r\) 增加 \(1\) 时，会影响到周边的 \(4\) 个 \(2×2\) 的小正方形，在线段树上区间加即可。

时间复杂度：\(\mathcal O(nm\log nm)\)。

P4898 [IOI 2018] seats 排座位

\(\text{Section 1}\) 转化

首先我们思考怎么对于一个 \(i\) 求出 \(S(i)\)。

与其他题解一样，我们将前 \(i\) 个点染为黑色，其余染成白色。

我们考虑使用染出来的颜色设计出 \(S(i)\) 为真的充要条件。

成为矩形的充要条件有：

• 点处于一个连通块内
• 图形不存在“\(\text{L}\) 型”。

对于条件 \(1\)，我们有：

• 对于所有黑点，其左上方两点中均不为黑色的点数为 \(1\)。

对于条件 \(2\)，我们有：

• 对于所有白点，与其四连通的点内有不少于两个黑点的个数为 \(0\)。

于是我们可以依次计算。

\(\text{Section 2}\) 优化

我们设点 \((i,j)\) 的编号为 \(num_{(i,j)}\)，编号为 \(i\) 的点为 \((x_i,y_i)\)。

考虑对于 \(\text{Section 1}\) 的算法将 \(i\) 由 \(1\) 枚举到 \(n\times m\)，则 \((i,j)\) 被染为黑色的时间点为 \(num_{(i,j)}\)。

我们考虑对于点 \((a,b)\)，其满足条件 \(1\)、\(2\) 的时间段。

设 \(i\) 为当前时间点。

此处我们不考虑边缘情况。

若满足条件 \(1\)，则：

• \((a,b)\) 是黑点，即 \(num_{(a,b)}\le i\)；
• \((a,b)\) 左方是白点，即 \(num_{(a-1,b)}>i\) ;
• \((a,b)\) 上方是白点，即 \(num_{(a,b-1)}>i\)。

对这些条件取并集，即 \(i\in[num_{(a,b)},\min(num_{(a-1,b)},num_{(a,b-1)}))\)。

若满足条件 \(2\)，则：

• \((a,b)\) 是白点，即 \(num_{(a,b)}>i\)；
• \((a,b)\) 四周 \(num\) 次小的值所在的点为黑点，即 \(\text{secmin}(num_{(a-1,b)},num_{(a,b-1)},num_{(a+1,b)},num_{(a,b+1)})\le i\)。

对这些条件取并集，即 \(i\in[\text{secmin}(num_{(a-1,b)},num_{(a,b-1)},num_{(a+1,b)},num_{(a,b+1)}),num_{(a,b)})\)。

此处需要搞清楚点被染黑点的条件、点被染成黑色的时间段等概念，不能混淆。

\(\text{Section 3}\) 数据结构

我们需要一种数据结构，支持上面的操作。

对于每个点我们维护 \([\) 满足条件 \(1\,]+[\) 满足条件 \(2\,]\)，那么我们对于每个合法区间进行 \(+1\)，查询全局有几个 \(1\)。

我们可以将满足条件一的点数设为 \(x\)，满足条件二的点数设为 \(y\)。

显然 \(x\ge 1,y\ge0\)，即 \(x+y\ge 1\)。

所以维护区间最小值及出现次数即答案.

\(\text{Section 4}\) 实现细节

• 1.线段树初始最小值为 \(0\) 情况的处理：

  我这里也采用了维护严格次小值及其出现次数的方法，查询判断最小值是否为 \(1\)，严格次小值是否为 \(1\) 即可。

• 2.修改点集出现重叠情况时需要去重。

• 3.我们将二维的 \(num\) 数组重编号为 \(1\) 至 \(n\times m\) 维护较为方便。

• 4.考虑边界问题，设计的重编号函数检测到越界时可以返回 \(n\times m+1\)，此时 \(num_{n\times m+1}=n\times m+1\)，线段树区间修改时判断当修改区间左端点大于右端点是返回即可。

---

最终时间复杂度为 \(O((nm+q)\log nm)\)。

线段树合并

概述

时间复杂度

对 \(n\) 棵线段树 \(T_i\)，以任意顺序进行线段树合并的总时间复杂度为：\(\mathcal O(\sum_{i=1}^n |T_i|-|\cup_{i=1}^nT_i|)\)。

证明：

采用数学归纳法。

• \(n=1\) 时显然成立。
• 不妨设 \(n\le k-1\) 时成立，考虑 \(n=k\) 时：
  • 将 \(n\) 棵线段树划分为任意两个集合 \(S_1,S_2\)，然后进行最后一次合并

根据归纳法：

\(\mathcal O((\sum_{i\in S_1}|T_i|-|\cup _{i\in S_1}T_i|)+(\sum_{i\in S_2}|T_i|-|\cup _{i\in S_2}T_i|))\)

化简得：

\(\mathcal O(\sum_{i=1}^k |T_i|-|\cup_{i\in s_1}T_i|-|\cup_{i\in s_2}T_i|)\)

我们再来计算合并 \(S_1,S_2\) 所需时间复杂度，最后一次合并时间复杂度=公共节点数量，因此为：

\(\mathcal O(|\cup_{i\in s_1}T_i|+|\cup_{i\in s_2}T_i|-|\cup_{i\in S_1}并上 \cup_{i\in S_2}|)\)

化简得：

\(\mathcal O(|\cup_{i\in s_1}T_i|+|\cup_{i\in s_2}T_i|-|\cup_{i=1}^nT_i|)\)

将两式相加得到总复杂度：\(\mathcal O(\sum_{i=1}^n |T_i|-|\cup_{i=1}^nT_i|)\)。

例题

P3224 [HNOI2012] 永无乡

联通块相关合并。

线段树合并板子题，我们维护的线段树需要支持查询全局权值第 \(k\) 小，直接权值线段树合并即可。

时间复杂度：\(\mathcal O(n \log n)\)。

P4197 Peaks

没有修改，考虑离线算法。我们可以离线下来，把所有询问按照 \(x\) 从小到大排序。

类似的，把所有边也按困难值从小到大排序。

这样一来，在处理询问的时候，如果要求的路径困难值 \(\le x\)，就把困难值 \(\le x\) 的边都加进来就可以了。

对于每个询问，加完边之后直接查询点所在连通块中的第 \(k\) 大，线段树上二分即可。

关于加边的方法，就要用到线段树合并。

时间复杂度：\(\mathcal O(n \log n)\)。

P3201 [HNOI2009] 梦幻布丁

我们对每一个颜色开一个线段树维护所有下标为这个颜色的集合。那么答案可以用线段树维护，把 \(x\) 变为 \(y\) 本质上就是把下标颜色为 \(x\) 的所有信息合并给 \(y\) 即可，这个过程可以线段树合并。

时间复杂度：\(\mathcal O(n \log n)\)。

P3302 [SDOI2013] 森林

主席树启发式合并好题。

发现我们要求路径上第 \(k\) 小权值，我们考虑使用主席树+差分维护即可。

但是我们支持合并，所以就用启发式合并，每次合并子树大小较小的那个子树到较大子树上面去，合并时要把路径信息用主席树维护下来，因为以后查询要差分。所以总复杂度为 \(\mathcal O(n \log^2 n)\)。

P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并

我们使用差分思想，先把修改信息就挂在 \(x\)，\(y\)，\(lca\)，\(fa_{lca}\) 上面，存储信息就用权值线段树即可，因为要求出现次数最多的值，最后求的是一个点的最多出现的值，我们使用线段树合并即可。时间复杂度：\(\mathcal O(n \log n)\)。

P7563 [JOISC 2021] 最悪の記者 4 (Worst Reporter 4) (Day4)

考虑 \(i\) 向 \(a_i\) 连边，构成一个内向基环树，注意题目要求祖先最后的 Rating 都比后代小。

先假设基环树为一棵树的情况。发现，当确定一些人的Rating时，且这些人的Rating已经满足了基环树限制的要求，那么剩下的人一定可以通过更改Rating来满足基环树条件限制。

问题转化为保留一定数量的点且满足限制关系，且这些点的 \(c\) 值之和最大，想到树形DP。

设 \(f_u\) 表示 \(u\) 这个点必须选，其子树中选择的点的最大值。那么有转移：

\[f_u=c_u+\max_{S\in T} \sum_{v\in S}f_v \]

其中 \(T\) 表示属于 \(u\) 的子树的点的集合，\(S\) 表示从 \(T\) 中选出一些点组成一个集合还要满足任意选出的两点没有祖先关系且Rating都大于 \(h_u\)。

发现这些点的选取集合 \(S\) 跟 \(h_u\) 有关，把 \(h_u\) 离散化后记转移式右边的值为 \(g_{u,i}\) 表示仅考虑那些 \(h_v\ge i\) 的点的答案。

这样转移方程就为 \(f_u=c_u+g_{u,h_u}\) 了。

转移 \(g\) 数组就是把各个儿子对应位置相加，再与父亲DP值在 \([1,h_u]\) 中依次取 \(\max\)，线段树合并维护。

现在线段树要支持区间取 \(\max\) 和加（合并操作就是区间加）。可以维护两个懒标记，先 \(\max\) 后加即可。

至于环上的话枚举将值修改成环上的哪一个值或者是全局最小值，取最大值统计答案。

时间复杂度：\(\mathcal O(n \log n)\)。

P6773 [NOI2020] 命运

复杂计数，考虑DP。

分析性质，对于当前点 \(x\) 和两个限制 \((u_1,v_1),(u_2,v_2),v_1 \in \operatorname{subtree}_x,v_2\in \operatorname{subtree}_x\)，如果 \(u_1\) 的深度小于 \(u_2\) 的深度，那么我们就只需考虑 \((u_2,v_2)\) 了，因为如果 \((u_2,v_2)\) 不能满足，那么最后肯定就不能满足所有限制了。

所以DP的后效性是什么呢？那不就是 \(x\) 子树内的限制 \((u,v)\) 中深度最大的 \(u_{\max}\) 才会对 \(x\) 产生真正的影响，如果 \((u_{\max},v)\) 被满足了那么 \(x\) 子树内所有限制都被满足了，否则我们需要把这个限制留给 \(x\) 的父亲处理，或者留给 \(x\) 的父亲的父亲处理……但是值得注意的是最后处理点的深度不能小于 \(u_{\max}\) 的深度，原因显然。

于是设 \(f_{x,i}\) 表示以 \(x\) 为根的子树中，两端点都在 \(x\) 子树中的限制已被满足，而对于尚未满足的限制 \((u,v)\)，且 \(u\) 在 \(x\) 子树外，\(v\) 在 \(x\) 子树内，最深的 \(u\) 的深度为 \(i\)。

考虑转移。对于一个点 \(x\)，考虑它的所有限制 \((u_1,x),(u_2,x),\cdots\)，设其中最深的 \(u\) 为 \(x\) 的 \(anc_x\)，如果没有这样的 \(u\) 则 \(anc_x=0\)。对于 \(f_{x,i}\)，我们有 \(\operatorname{dep}_{anc_x}\le i <\operatorname{dep}_{x}\)，因为对于限制 \((anc_x,x)\)，无论你怎么给 \(x\) 子树染色都不可能满足限制。那么枚举 \(x\) 的所有儿子 \(y\) 开始转移：

1. 对 \((x,y)\) 染色

   那么所有端点 \(v\) 在 \(y\) 内的限制全部得到满足。所以贡献为：

   \[f_{x,i}\times \sum_{\operatorname{dep}_{anc_y}\le j <\operatorname{dep}_y}f_{y,j} \]

   为了方便转移，设 \(g_{x,i}\) 为 \(f\) 前缀和：\(g_{x,i}=\sum_{j=0}^i f_{x,i}\)，由于对于 \(j<\operatorname{dep}_{anc_x}\)，\(f_{x,j}\) 都为 \(0\)，所以定义是合法的。

   所以贡献为：

   \[f_{x,i}\times g_{y,\operatorname{dep}_y-1} \]

2. 对 \((x,y)\) 不染色

   1. 如果本来 \(x\) 子树中最深的限制是等于 \(i\) 的，那么因为要求合并后整个子树的限制仍然是 \(i\)，那么 \(y\) 子树内的限制就只能 \(\le i\)，所以贡献为：

      \[f_{x,i}\times g_{y,i} \]

   2. 如果本来 \(x\) 子树中最深的限制是小于 \(i\) 的，那么就只能让 \(y\) 子树的限制是 \(i\)，所以贡献为：

      \[f_{y,i}\times g_{x,i-1} \]

综上所述，最后转移为：

\[f_{x,i'}\leftarrow f_{x,i}\times g_{y,\operatorname{dep}_y-1}+f_{x,i}\times g_{y,i}+f_{y,i}\times g_{x,i-1}(\operatorname{dep}_{anc_x}\le i<\operatorname{dep}_x) \]

化简得：

\[f_{x,i'}\leftarrow f_{x,i}\times (g_{y,\operatorname{dep}_y-1}+g_{y,i})+f_{y,i}\times g_{x,i-1}(\operatorname{dep}_{anc_x}\le i<\operatorname{dep}_x) \]

初始值：\(f_{x,\operatorname{dep}_{anc_x}}=1\)

答案：\(f_{1,0}\)。

时间复杂度：\(\mathcal O(\min(n,m)^2)\)。

期望得分：\(72pts\)。

考虑优化，DP优化有两个基本方向，状态数和转移，状态已经不能再优化了，所以只能优化转移，发现转移可以轻松用线段树合并优化。

但是观察上式转移，发现是 \(f_{x,i}\) 乘上某个数再加上 \(f_{y,i}\) 乘上某个数，“某个数”还会变。

考虑维护两个值：\(sum_x,sum_y\)，表示 \(f_{x,i},f_{y,i}\) 的前缀和，那么设当前线段树合并时两个子树 \(x,y\)，考虑操作：

• \(x=0,y=0\) 直接返回。
• \(x=0,y\ne 0\)，说明 \(sum_x\) 不会发生变化，且所有 \(f_{x,i}\) 没有值，就相当于子树乘一个数 \(g_{x,i-1}\)。
• \(x\ne 0,y=0\)，说明 \(sum_y\) 不会发生变化，且所有 \(f_{y,i}\) 没有值，就相当于子树乘一个数 \((g_{y,\operatorname{dep}_y-1}+g_{y,i})\)。
• \(x\ne 0,y\ne 0\)，继续向下合并，最后 \(\operatorname{pushup}\) 一下即可。

而后需要注意 , 对于 \(f_{x,i}\), 由于只有 \(\operatorname{dep}_{anc_x}≤i<\operatorname{dep}_{x}\) 会有值 , 所以处理完子树转移后 , 我们需要将 \([0,\operatorname{dep}_{anc_x})\) 和 \([\operatorname{dep}_{x},n]\) 区间赋值为 0。

所以只用维护两个懒标记即可，区间赋值相当于乘法懒标记置为 \(0\)。

时间复杂度：\(\mathcal O(n \log n)\)。

P8496 [NOI2022] 众数

用权值线段树维护每个数出现的次数，链表维护序列。

操作 4 即合并两棵权值线段树、两个链表，操作 2 就是删除链表尾的元素并在权值线段树上修改。

显然，如果一个序列存在绝对众数，那么它必然等于这个序列的中位数。所以操作 3 就是询问 \(k\) 个序列整体的中位数，并检查这个数的出现次数。

考虑二分中位数，在 \(k\) 棵线段树上分别查询前缀和，再判断出现次数，然而时间复杂度是 \(\mathcal O(n\log^2 n)\)，可能无法通过。把二分中位数改成在 \(k\) 棵线段树上二分即可做到 \(\mathcal O(n\log n)\)。

UVA1479 Graph and Queries

时间倒流即可（使用离线算法+线段树合并——权值线段树合并）。

时间复杂度：\(\mathcal O(n \log n)\)。

P10241 [THUSC 2021] 白兰地厅的西瓜

求树上 LIS。

考虑线段树合并。

对每个点开一棵线段树记录从它的子树里的某个点到这个点的路径上且吃过的最后一个西瓜的美味值为 \(u\) 的最长上升子序列长度，还有最长下降子序列长度以及最后一个西瓜的美味值。

那么我们在 \(u\) 点合并信息即可。即答案就是所有 \(u\) 点所记录的最长上升子序列长度再加上最长下降子序列长度即可，要满足最长上升子序列的最后一个元素小于最长下降子序列的最后一个元素才能更新。还要注意线段树合并的时候也要更新答案，即有可能不吃 \(u\) 点的西瓜。

习题：

[P3605 USACO17JAN] Promotion Counting P - 洛谷

CF208E Blood Cousins - 洛谷

CF911G Mass Change Queries - 洛谷 线段树合并分裂板子题。

线段树二分

概述

着重说一下它的时间复杂度。

在区间 \([l,r]\) 之间询问，那么二分就是在 \([l,r]\) 中二分，那么我们已知可以把 \([l,r]\) 拆为 \(\log n\) 个区间，询问时要么从左往右询问每个区间，要么从右往左询问每个区间，所以就和普通的询问在线段树上询问一个区间的信息一样，为 \(\mathcal O(\log n)\)。

例题

CF1268C K Integers

线段树二分好题。

考虑将这个过程拆为两步：

1. 先把 \([1,k]\) 移到一起。
2. 再将 \([1,k]\) 排序。

我们发现第二步很好处理，\([1,k]\) 排序就相当于求解逆序对。难点在第一步，我们发现其贡献就是 \(\min(i-L-pre_i,R-i-nxt_i)\)，\([L,R]\) 表示在原序列中最小的包含 \([1,k]\) 中的数，\(pre_i\) 表示 \([L,R]\) 中有多少个 \(j\) 在 \(i\) 的前面且 \(p_j>k,p_i>k\)，然后我们发现上式贡献具有单调性，可以使用二分。

Segment Tree beats/吉司机线段树

适用于对区间取 \(\max,\min\) 的情况，即 \(\forall i\in[l,r]\)，\(a_i \leftarrow \min(a_i,x),a_i \leftarrow \max(a_i,x)\)，这样的操作。

首先直接用线段树是肯定不好做的，信息不好维护，但是区间取 \(\min\)，意味着只对那些大于 \(x\) 的数产生影响。于是我们考虑维护四个值 \(mx,se,cnt,sum\)，分别表示当前线段树上的节点所对应的区间的最大值、严格次大值、最大值出现次数，以及整个区间所有元素的和。注意初始值为 \(se=-1\)

考虑一次修改操作 \((l,r,x)\)：

• \(mx\le x\)，显然此时这个操作是毫无影响的，它不会使区间中任何一个值改变。
• \(se<x<mx\)，此时这个 \(x\) 就只能更新这个区间的最大值的值，此时 \(\Delta_{sum}=cnt\times(x-mx)\)，然后 \(mx \leftarrow x\)，并打上一个标记。
• \(x \le se\)，此时暴力往这个节点的左右子区间递归修改，然后再 pushup。

再考虑这样做的时间复杂度，读者可能唯一疑惑的地方在于第三种情况，暴力更新的时间复杂度真的是对的吗？我们可以使用势能分析来计算复杂度：

先给出结论复杂度为：\(\mathcal O(q\log n+n\log^2 n)\)。

首先在线段树上定位需要花费 \(q\log n\) 的时间复杂度。

然后我们再定义 \(φ(u)\) 为：\(u\) 的子树中满足自己的最大值与它父节点最大值不相等的节点个数。那么我们每次暴力递归显然总势能（所有 \(φ(u)\) 的和）的上界显然是 \(\mathcal O(n\log n)\)。那么我们每往下暴力递归一次都会使势能减少 \(1\)，因为 \(se,mx\) 不相等说明 \(u\) 子树内一定有一个点满足其父亲的 \(mx\) 和自己的 \(mx\) 不相等，递归到这个点 \(u\) 的时候就更改信息，减少了势能，每个节点最多被暴力修改一次，复杂度为 \(\mathcal O(\log n)\) 所以复杂度为 \(\mathcal O(n\log^2 n)\)。

P10338 [THUSC 2019] 彩票

先推出一个重要性质：

当总彩票为 \(x+y\)，其中中奖券有 \(x\) 张，空奖券有 \(y\) 张时，抽出一张彩票后，这张彩票为中奖券的概率为 \(\frac{x}{x+y}\)。

那么再抽第二张彩票呢？

抽到中奖券概率就是：

\[\frac{x}{x+y}\times \frac{x-1}{x+y-1}+\frac{y}{x+y}\times \frac{x}{x+y-1}=\frac{x\times (x+y-1)}{(x+y-1)\times (x+y)}=\frac{x}{x+y} \]

但是上述的性质并不完全正确，有一种情况例外，那就是全部抽完，那么此时抽出彩票的概率就变成 0 了。

那么回到本题上来，我们需要实现这几个操作：

1. 抽奖券
   • 当没有抽完，单点答案加上 \(c\times \frac{x}{x+y}\)，这种情况 \(\mathcal O(\log n)\) 修改即可。
   • 如果抽完，单点答案加上 \(x\)，这种情况有点复杂，不好直接修改。
2. 询问答案，直接用线段树 \(\mathcal O(\log n)\) 回答询问即可。
3. 单点修改，直接 \(\mathcal O(\log n)\) 修改即可。

可以看到上述分析，只有第一个操作的第二种情况我们好像无法用线段树处理。

但是我们发现一个抽奖箱被抽完的次数只有 \(\mathcal O(n+q)\) 次。

那么可以考虑类似势能线段树的东西来维护这个操作。

具体地，势能线段树维护区间抽奖箱中拥有抽奖券数量最少的抽奖箱的抽奖箱的数目 \(mi_x\)。

再来考虑修改。

• 当整个区间的 \(mi_x\) 都大于等于 \(c\) 时我们就可以直接修改答案和 \(mi_x\)。
• 否则，我们暴力往下递归，去寻找那些抽奖券小于 \(c\) 的抽奖箱并暴力修改即可。

那么这样的复杂度是多少呢？

因为根据上面的『一个抽奖箱被抽完的次数只有 \(\mathcal O(n+q)\) 次』，可以得到只有 \(\mathcal O(n+q)\) 次暴力往下递归并修改。这个复杂度就是 \(\mathcal O((n+q)\log n)\) 的。

！注意：这题 pushdown 的时候要格外小心！！！

即当彩票数为 \(0\) 时，就不用再减去了！！！不然会错，此题锻炼了细节讨论能力。

3356 -- 【牛客网2020day6】牛半仙的妹子序列

再次被看错题薄纱。

题目是求解极长上升子序列个数。

那么考虑一个DP，设 \(f_i\) 表示以 \(i\) 结尾的极长上升子序列个数。那么显然转移方程为 \(f_i \leftarrow f_j\)。

但是这个 \(j\) 要满足哪些条件呢？其实 \(j\) 就是 \([1,i-1]\) 中单调栈（单调栈为栈底最小）中**小于 \(a_i\) **的元素。

再捋一遍，合法的 \(j\) 就是：

• \(j<i\)。
• \(p_j<p_i\)。
• 不存在 \(j<k<i\)，使得 \(p_j<p_k<p_i\)。

发现如果我们定 \(i\) 的话，还要对 \(j<i,p_j<p_i\) 建立单调栈后再进行贡献计算。也就是说 \(i\) 要维护出一个单调栈，这个东西很难维护，因为我们扫的就是 \(i\)，每扫到一个 \(i\) 我们就要快速维护出关于 \(i\) 的单调栈，要想维护出只能遍历到 \(j\) 时对所有 \(i,p_i>p_j,top_i>p_j\) 的单调栈都压入 \(p_j\)，这是不现实的，因为无法快速找到这样的 \(i\)，即这样的 \(i\) 不连续。那么正难则反，我们考虑 \(j\) 会对哪些 \(i\) 产生贡献，也就是说我们尝试对 \(j\) 建立单调栈，这样每扫到一个 \(i\) 时就可以维护出变化量即可。

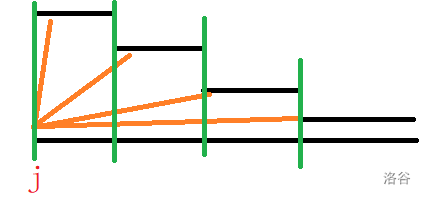
看上图会发现，\(j\) 产生的贡献的 \(i\) 满足 \(i>j,p_i>p_j\)，且 \(i\) 也满足单调栈的性质。也就是说我们 \(j\) 也要维护一个单调栈。

难道这个东西就不能做了吗？不是的，当我们扫到 \(i\) 时，只需要 \(j<i,top_j>p_i,p_j<p_i\) 这样的 \(j\) 就可以向 \(i\) 产生贡献了。我们维护 \(top\)，然后扫到 \(i\) 时就相当于是先把 \([1,p_i-1]\) 内的数的 \(top\) 都 \(\text{chkmn}\) 一下，然后所有的 \(j\in[1,p_i-1]\) 满足 \(top_j=p_i\) 的 \(j\) 就可以转移到 \(i\) 了。

参考代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>
#define MAXN 200005
using namespace std;
const int MOD=998244353,INF=0x3f3f3f3f;
inline int add(const int& x,const int& y){return x+y>=MOD? x+y-MOD:x+y;}
inline int read()
{
	int ans=0;
	char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
int f[MAXN];
#define lc p<<1
#define rc p<<1|1
struct node{int mx,se,sum;}t[MAXN<<2];
int lzy[MAXN<<2];
inline node merge(node a,node b)
{
	if (a.mx==b.mx)	a.se=max(a.se,b.se),a.sum=add(a.sum,b.sum);
	else
	{
		if (a.mx<b.mx) swap(a,b);
		a.se=max(a.se,b.mx);
	}
	return a;
}
inline void pushlzy(int p,int v){t[p].mx=min(t[p].mx,v),lzy[p]=min(lzy[p],v);}
inline void pushdown(int p)
{
	if (lzy[p]<INF)
	{
		pushlzy(lc,lzy[p]),pushlzy(rc,lzy[p]);
		lzy[p]=INF;
	}
}
void modify(int p,int l,int r,int k,int v)
{
	if (l==r) return (void)(t[p].mx=INF,t[p].sum=v);
	int mid=(l+r)>>1;
	pushdown(p);
	if (k<=mid) modify(lc,l,mid,k,v);
	else modify(rc,mid+1,r,k,v);
	t[p]=merge(t[lc],t[rc]);
}
void modify(int p,int l,int r,int ql,int qr,int v)
{
	if (ql<=l&&r<=qr&&v>t[p].se) return pushlzy(p,v);
	if (qr<l||r<ql) return;
	int mid=(l+r)>>1;
	pushdown(p);
	modify(lc,l,mid,ql,qr,v),modify(rc,mid+1,r,ql,qr,v);
	t[p]=merge(t[lc],t[rc]);
}
node ans;
void query(int p,int l,int r,int ql,int qr)
{
	if (ql<=l&&r<=qr)
	{
		if (ql==l) ans=t[p];
		else ans=merge(ans,t[p]);
		return;
	}
	if (qr<l||r<ql) return;
	pushdown(p);
	int mid=(l+r)>>1;
	query(lc,l,mid,ql,qr),query(rc,mid+1,r,ql,qr);
}
int main()
{
	memset(lzy,0x3f,sizeof(lzy));
	int n=read();
	for (int i=1;i<=n;i++)
	{
		int v=read();
		modify(1,1,n,1,v,v),query(1,1,n,1,v);
		f[i]=(ans.mx==v? ans.sum:0);
		if (!f[i]) f[i]=1;
		modify(1,1,n,v,f[i]);
	}
	printf("%d\n",t[1].sum);
	return 0;
}

这里还有种很妙的做法。它巧妙的把 \(a_j\le a_i\) 给规避掉了—— 按照 \(a[i]\) 大小依次加入点，线段树维护单调栈即可。

int stk[MAXN], top;

int lim;
int mx[MAXN << 2];
int visib[MAXN << 2];

int pre[MAXN], suf[MAXN];
int att[MAXN], dp[MAXN], pos[MAXN];
int N;

inline int Mul( int x, int v ) { return 1ll * x * v % mod; }
inline int Sub( int x, int v ) { return ( x -= v ) < 0 ? x + mod : x; }
inline int Add( int x, int v ) { return ( x += v ) >= mod ? x - mod : x; }

int Calc( const int x, const int l, const int r, const int lim ) {
    if( l == r ) return lim < mx[x] ? dp[l] : 0;
    int mid = ( l + r ) >> 1;
    if( lim >= mx[x << 1 | 1] ) return Calc( x << 1, l, mid, lim );
    return Add( visib[x], Calc( x << 1 | 1, mid + 1, r, lim ) );
}

inline void Upt( const int x, const int l, const int r ) {
    int mid = ( l + r ) >> 1;
    mx[x] = MAX( mx[x << 1], mx[x << 1 | 1] );
    visib[x] = Calc( x << 1, l, mid, mx[x << 1 | 1] );
}

void Change( const int x, const int l, const int r, const int p, const int nVal ) {
    if( l == r ) { mx[x] = nVal; return ; }
    int mid = ( l + r ) >> 1;
    if( p <= mid ) Change( x << 1, l, mid, p, nVal );
    else Change( x << 1 | 1, mid + 1, r, p, nVal );
    Upt( x, l, r );
}

int Query( const int x, const int l, const int r, const int segL, const int segR ) {
    if( segL > segR ) return 0;
    if( segL <= l && r <= segR ) {
        if( mx[x] <= lim ) return 0;
        int ret = Calc( x, l, r, lim );
        lim = mx[x]; return ret;
    }
    int mid = ( l + r ) >> 1, ret = 0;
    if( mid  < segR ) ret = Add( ret, Query( x << 1 | 1, mid + 1, r, segL, segR ) );
    if( segL <= mid ) ret = Add( ret, Query( x << 1, l, mid, segL, segR ) );
    return ret;
}

int main() {
    read( N );
    rep( i, 1, N ) read( att[i] ), pos[att[i]] = i;
    pre[0] = N, suf[N] = 0;
    rep( i, 1, N ) pre[i] = MIN( pre[i - 1], att[i] );
    per( i, N, 1 ) suf[i] = MAX( suf[i + 1], att[i] );
    int ans = 0;
    rep( v, 1, N ) {
        int i = pos[v];
        if( pre[i - 1] >= v ) dp[i] = 1;
        else lim = 0, dp[i] = Query( 1, 1, N, 1, i - 1 );
        if( suf[i + 1] <= v ) ans = Add( ans, dp[i] );
        Change( 1, 1, N, i, v );
    }
    write( ans ), putchar( '\n' );
    return 0;
}

st表

堆

左偏堆

可删堆

主席树

概述

例题

P4732 [BalticOI 2015] Editor

设第 \(i\) 次撤销操作要撤销的是 \(j\)，那么 \(i\) 到 \(j\) 的操作中不存在优先级比 \(j\) 小的，所以 \(j\) 到 \(i\) 的操作不会在没撤销 \(i\) 的情况下被撤销。

考虑可持久化线段树，维护操作的优先级，撤销操作 \(i\) 直接继承 \(j−1\) 的版本，查询 \(j\) 直接线段树上二分。

时间复杂度：\(\mathcal O(n \log n)\)。

4205 -- 【BZOJ4771】七彩树

如果没有深度限制，每次只询问子树内的颜色个数，除了树套树 dfs 序加前驱或者后继强行二维数点之外，还有这样一种做法：
把所有相同颜色的点按照dfn序排序，每个点给自己的位置贡献 \(1\)，相邻的两个点给 lca 贡献 \(−1\)。然后只要区间内存在这种颜色，则其子树内的权值和必定为 \(1\)。那么只需要这样子染好所有颜色之后询问子树和。
然而这题要求的是深度在一个范围内的东西。
如果可以离线，我们可以把所有点按照深度排序，从上往下依次加入，计算贡献，然后把询问在 \(dep[x]+d\) 的地方计算答案。
现在不能离线，就提前把这个东西的线段树给算好，拿主席树直接提前维护好就行了。
时间复杂度是一个 \(\log\)。

树套树

前置知识：动态开点线段树。

树套树是在树形数据结构的结点内部套一层树形数据结构。为方便说明，分别记为外层结构和内层结构。

树套树的常见形式有线段树套线段树，树状数组套线段树，以及线段树套平衡树。

树状数组套线段树

BIT 套动态开点线段树可解决带修二维数点等经典问题。注意当值域过大时需将外层结构换成动态开点线段树。

线段树套线段树

真正的树套树。

线段树套线段树也称二维线段树，是信息不具有可减性时树状数组套线段树的替代品，如查询矩形内点权最值。使用方法是把外层结构从树状数组换成线段树。

例题

P3380 【模板】树套树

板子。

平衡树

例题

P11622 [Ynoi Easy Round 2025] TEST_176

平衡树有交合并板子。参考资料：数据结构 Trick 之：平衡树有交合并 - 洛谷专栏

\(x=\max(x,a_i−x)\) 这样的操作无法合并，并且与变量 \(x\) 相关，无法使用一般线段树维护。

考虑操作实质：若 \(x<⌊\frac{a_i}{2}⌋\)，则令 \(x\leftarrow a_i−x\)。

那我们可以考虑对于任意一个经过 \(a_i\) 的 \(x\)：

• \(x←a_i−x\)，\(x∈(−∞,⌊\frac{a_i}{2}⌋)\)
• \(x\) 不变，$$x∈[⌊\frac{a_i}{2}⌋,+∞)$$

这一类询问区间可拆、关于值域的操作可以使用扫描线+平衡树维护。

具体地：

1. 将询问离线。
2. 遍历 \(a\) 数组，对于每个 \(i\)，遍历若干个左端点为 \(i\) 的区间，将对应的 \(x\) 插入平衡树。
3. 把平衡树上小于 \(⌊\frac{a_i}{2}⌋\) 的元素改为 \(a_i−x\)。这里可以在平衡树上打标记，注意下传时先乘后加，加法标记也要乘 \(−1\)，左右儿子互换等。
4. 对于每个 \(i\)，遍历若干个右端点为 \(i\) 的区间，将对应的 \(x\) 取出值。
5. 按序输出。

特别的，第三步中涉及平衡树合并操作。显然第三步拆分出的其中一棵树在操作后和另一棵树值域有交，这是 FHQ-Treap 的 merge 操作无法实现的。

时间复杂度：和 beats 的时间复杂度差不多。复杂度上限为 \(\mathcal O(n \log^2 n)\)，但一般与 \(\mathcal O(n \log n)\) 表现差不多。

注意：本题很卡常。

并查集

普通并查集

应用

例题

P5610 [Ynoi2013] 大学

太太太卡常了！！！

首先我们发现一个性质，就是每一个数最多被除 \(\mathcal O(\log n)\) 次就会变成 \(1\)，所以只要能够做到只处理需要修改的位置的修改就可以做到一个正确的复杂度。

所以这个复杂度瓶颈实际上是在于如何快速找到需要修改的位置。

我们发现每一个数的约数个数大约是 \(\mathcal O(\sqrt[3]{a})\) 的，所以我们对于每一个数 \(i\) 用一个数据结构来维护所有 \(i\) 的倍数。

我们来看需要支持什么操作：

• 查询一个数的值；
• 计算 \(\operatorname{lower\_bound}\)；
• 删除；

我们考虑对每一个位置维护一个指针指向它之后的第一个没有被删除的元素，初始的时候显然都指向自己。

如果我们要删除第 \(i\) 个元素，那么它的指针的新位置肯定是 \(i+1\) 的指针指向的位置（如果是最后一个元素那么就是空）；这个可以感性理解一下。

查询和 \(\operatorname{lower\_bound}\) 的时候就直接访问指针就好。

显然我们可以用一个并查集来维护这些指针，这样上述三个操作都能做到 \(\mathcal O(\alpha (n))\)。

卡卡常数即可。鉴于此题有点抽象，现直接给出代码，细节可以参考代码。

const int N=5e5+50,M=25000050,inf=2e9,mod=998244353;
int T;
int n,m,ct;
int poolv[M],poolnxt[M],cntv[N],cnta[N],head[N],a[N];
int *v[N],*nxt[N];
ll ans; 
struct BIT{
	ll tree[N];
	inline void update(int k,int x)
	{
		for(;k<=n;k+=lowbit(k))
			tree[k]+=x;
	}
	inline ll query(int k)
	{
		ll res=0;
		for(;k>0;k-=lowbit(k))
			res+=tree[k];
		return res;
	}
}G;
struct List{
	int val,nxt;
	List(){
		nxt=-1;
	}
}e[10000050];//用来存储i的因子 
inline void add(int u,int v)
{
	e[++ct].val=v;
	e[ct].nxt=head[u];
	head[u]=ct;
}
inline int Find(int i,int x)
{
	if(x==cntv[i]||nxt[i][x]==x)return x;//并查集维护下一个有值的相对位置，没有则返回 
	return nxt[i][x]=Find(i,nxt[i][x]);
}
inline void update(int l,int r,int x)
{
	int pos=Find(x,lower_bound(v[x],v[x]+cntv[x],l)-v[x]);
	while(pos<cntv[x]&&v[x][pos]<=r)
	{
		if(a[v[x][pos]]%x==0)
		{
			G.update(v[x][pos],a[v[x][pos]]/x-a[v[x][pos]]);
			a[v[x][pos]]/=x;
		}
		int t=Find(x,pos+1);
		if(a[v[x][pos]]%x)nxt[x][pos]=t;
		pos=t;
	}
}
inline void solve()
{
	read(n);read(m);
	for(re int i=1;i<=n;i=-~i)read(a[i]),G.update(i,a[i]),cnta[a[i]]++;
	for(re int i=1;i<=500000;i=-~i)
	{
		for(re int j=i;j<=500000;j+=i)//预处理出因子 
		{
			add(j,i);
			cntv[i]+=cnta[j];
		}
	}
	int vtop=0,nxttop=0;
	for(re int i=1;i<=500000;i=-~i)
	{
		v[i]=poolv+vtop;nxt[i]=poolnxt+nxttop;//预处理出内存池
		vtop+=cntv[i]+3;nxttop+=cntv[i]+3;
		cntv[i]=0;
	}
	for(re int i=1;i<=n;i=-~i)
	{
		for(int j=head[a[i]];j;j=e[j].nxt)
		{
			int x=e[j].val;
			v[x][cntv[x]]=i;nxt[x][cntv[x]]=cntv[x];
			cntv[x]++;//v表示这个数在原序列的位置 nxt表示下一个有值的相对位置 
		}
	}
	while(m--)
	{
		ll op,l,r;
		read(op);read(l);read(r);l^=ans;r^=ans; 
		if(op==1)
		{
			ll x;read(x);x^=ans;
			if(x==1)continue;
			update(l,r,x);
		}
		else
		{
			ans=G.query(r)-G.query(l-1);
			write(ans,'\n');
		}
	}
}
signed main()
{
	T=1;
	while(T--)solve();
	return 0;
}

时间复杂度：\(\mathcal O(n\log n \log v)\)。

7714 -- 【10.19模拟】方案数

由于本题是将序列划分成两个部分，那么我们如果有两个数 \(u,v\)，且它们满足 \(\gcd (u,v)\ne 1\) 时，那么我们一定要给它们划分到一个集合当中，原因显然。那就在 \(u,v\) 之间连一条边。

最后图一定是被分为了几个连通块，任意两个连通块 \(S_1,S_2\) 之间的数 \(u \in S_1,v \in S_2\) 的 \(\gcd\) 都是 \(1\)，那么我们就可以把它们到一个集合中，最后方案数就是 \(2^{cnt}\)。

那怎么求解出 \(cnt\) 呢？我们枚举每个 \(a_i\) 的质因子，将质因子作为代表元，\(i\) 就向这个质因子连边，发现可以用并查集来维护即可。

时间复杂度：由于一个数最多拥有 \(\log V\) 个质因子，所以复杂度为 \(\mathcal O(n\log V)\)。

带权并查集

概述

例题

P4079 [SDOI2016] 齿轮

我们伟大的jzp把带权并查集合并归到了启发式合并里，很迷惑。

带权并查集板题。

笛卡尔树

区间笛卡尔树

例题

CF1117G Recursive Queries

观察 \(f(l,r)\) 的式子，其本质就是建区间笛卡尔树，然后答案就是每个点在笛卡尔树中的深度之和。

显然我们不能对于每次询问都建一棵笛卡尔树，所以我们尝试在整个数组的笛卡尔树上做些文章。但如果我们把一个区间在整个数组的笛卡尔树上表示出来，区间中的节点可能非常分散，不好处理。

观察线性构建笛卡尔树的算法，它是一个在线算法。也就是说，我们可以得到所有区间 \([1,r](1\le r\le n)\) 的笛卡尔树。我们尝试在区间 \([l,r]\) 在 \([1,r]\) 的笛卡尔树表示出来。

记区间 \([l,r]\) 中最大值出现位置为 \(mid\)，则对于区间 \([l,r]\) 的笛卡尔树，\(mid\) 是它的根节点，根节点的右子树是区间 \([mid+1,r]\) 的笛卡尔树。

考虑另一种构建笛卡尔树的算法：每次取出当前区间的最大值，然后递归处理左右区间。那么对于区间 \([l,r]\) 的笛卡尔树，\(mid\) 一定是 \([l,r]\) 中最先被取出的，即 \(mid\) 的深度是 \([l,r]\) 中最小的。\(mid\) 被取出后，\([mid+1,r]\) 就成为了它的右区间，即 \(mid\) 的右子树是区间 \([mid+1,r]\) 的笛卡尔树。

可以发现，我们可以在区间 \([1,r]\) 的笛卡尔树上得到区间 \(mid+1,r\) 的笛卡尔树。对于区间 \(l,mid-1\) 的笛卡尔树，可以把整个数组翻转，用同样的方法得到。它们合起来就是区间 \([l,r]\) 的笛卡尔树。

那么我们在构建笛卡尔树时，要动态修改每个节点的深度，并查询区间 \([mid+1,r]\) 中所有节点的深度之和以及 \(mid\) 的深度（由于 \(mid\) 的深度不一定为 \(1\)，要注意减掉 \(mid\) 的深度带来的影响）。这是一个区间加、区间求和的问题，用树状数组或线段树维护即可。

还有一个问题就是如何快速找到 \(mid\)。考虑单调栈维护的是从根节点开始不断往右儿子走形成的链。由于 \(r\) 一定在这条链上，且 \(r\) 在 \(mid\) 的右子树中，所以 \(mid\) 也在这条链上。由于 \(mid\) 的深度是 \([l,r]\) 中最小的，所以我们在单调栈上二分，第一个满足编号 \(\ge l\) 的节点就是 \(mid\)。

时间复杂度：\(\mathcal O((n+q)\log n)\)。

#define int long long
const int N=1e6+50,M=2e6+50,inf=2e9,mod=998244353;
struct node{
	int sum,tag;
};
struct Que{
	int l,r,id;
	bool operator <(const Que&a)const{
		return r<a.r;
	}
}a[N];
struct SegmentTree{
	node t[N*4];
	void cle(){memset(t,0,sizeof(t));}
	void pushup(int p){t[p].sum=t[p*2].sum+t[p*2+1].sum;}
	void f(int p,int l,int r,int k){t[p].sum+=(r-l+1)*k;t[p].tag+=k;}
	void pushdown(int p,int l,int r)
	{
		if(t[p].tag)
		{
			f(p*2,l,mid,t[p].tag);f(p*2+1,mid+1,r,t[p].tag);
			t[p].tag=0;
		}
	}
	void update(int p,int l,int r,int x,int y,int k)
	{
		if(x<=l&&r<=y)
		{
			f(p,l,r,k);
			return;
		}pushdown(p,l,r);
		if(x<=mid)update(p*2,l,mid,x,y,k);
		if(y>mid)update(p*2+1,mid+1,r,x,y,k);
		pushup(p);
	}
	int query(int p,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y)return t[p].sum;
		pushdown(p,l,r);int res=0;
		if(x<=mid)res+=query(p*2,l,mid,x,y);
		if(y>mid)res+=query(p*2+1,mid+1,r,x,y);
		return res;
	}
}T;
int n,q,top;
int stk[N],p[N],ans[N];
signed main()
{
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>q;
	for(int i=1;i<=n;i++)cin>>p[i];
	for(int i=1;i<=q;i++)cin>>a[i].l,a[i].id=i;
	for(int i=1;i<=q;i++)cin>>a[i].r,ans[i]=a[i].r-a[i].l+1;
	sort(a+1,a+1+q);int pos=1;
	for(int i=1;i<=n;i++)
	{
		int pre=top;
		while(top&&p[i]>p[stk[top]])top--;
		if(top)
		{
			int res=T.query(1,1,n,stk[top],stk[top]);
			T.update(1,1,n,i,i,res+1);
		}else T.update(1,1,n,i,i,1);
		if(pre!=top)T.update(1,1,n,stk[top]+1,i-1,1);
		stk[++top]=i;
		while(a[pos].r==i&&pos<=q)
		{
			int x=lower_bound(stk+1,stk+1+top,a[pos].l)-stk;
			x=stk[x];
			ans[a[pos].id]+=T.query(1,1,n,x+1,i)-(i-x)*T.query(1,1,n,x,x);
			pos++;
		}
	}
	reverse(p+1,p+1+n);
	for(int i=1;i<=q;i++)
	{
		swap(a[i].l,a[i].r);
		a[i].l=n-a[i].l+1;
		a[i].r=n-a[i].r+1; 
	}sort(a+1,a+1+q);
	T.cle();top=0;pos=1;
	for(int i=1;i<=n;i++)
	{
		int pre=top;
		while(top&&p[i]>p[stk[top]])top--;
		if(top)
		{
			int res=T.query(1,1,n,stk[top],stk[top]);
			T.update(1,1,n,i,i,res+1);
		}else T.update(1,1,n,i,i,1);
		if(pre!=top)T.update(1,1,n,stk[top]+1,i-1,1);
		stk[++top]=i;
		while(a[pos].r==i&&pos<=q)
		{
			int x=lower_bound(stk+1,stk+1+top,a[pos].l)-stk;
			x=stk[x];
			ans[a[pos].id]+=T.query(1,1,n,x+1,i)-(i-x)*T.query(1,1,n,x,x);
			pos++;
		}
	}
	for(int i=1;i<=q;i++)cout<<ans[i]<<" ";
	return 0;
}

笛卡尔重构树/Kruskal 重构树

例题

P10795 『SpOI - R1』Lamborghini (Demo)

注意到 \(t_i\) 互不相同。

那么我们按照 \(t_i\) 从大到小排序，依次加入点，建立笛卡尔重构树。

问题转化为对于每一个加入的点 \(u\)，统计有多少个已经加入的点对 \((x,y)\)，满足 \(v_x\le v_u \le v_y\)。这个东西可以用权值线段树来维护，然后因为每次都要加点和询问一个连通块的值域信息，我们考虑线段树合并维护。

时间复杂度：\(\mathcal O(n \log n)\)。

代码不难写，就不放了。

7688 -- 【10.03模拟】超级加倍

很容易写出暴力点分治，但是因为需要解决二维偏序问题所以是 \(\mathcal O(n\log^2n)\) 的。

首先考虑树是一条链的情况，发现可以二分求出 \(i\) 的范围，然后在这个范围中看有多少 \(j\) 即可。

那么搬到树上我们需要解决求出范围这个问题，既然它又是路径最值问题我们可以使用重构树，我们从大到小加入节点，对于新加的节点 \(u\)，我们看所有边 \((u,v)\) 并且 \(v\) 已经被加入了，那么我们合并 \(u\) 和 \(v\) 连通块的根，并且把 \(v\) 并查集的根设置成 \(u\)，可以用并查集简单维护。

那么重构树上两个点的 \(\texttt{lca}\) 就是它们真实路径上的最小值，用类似的方法可以求出第二棵树使得 \(\texttt{lca}\) 就是它们真实路径上的最大值。那么条件转化成第一棵树上 \(x\) 是 \(y\) 的祖先，第二棵树上 \(y\) 是 \(x\) 的祖先，我们可以求出第一棵树上的 \(\texttt{dfn}\) 序，在第二棵树上 \(\texttt{dfs}\)，用树状数组来统计答案，时间复杂度 \(\mathcal O(n\log n)\)。

对重构树的理解不仅仅是最小生成树上的边重构，还可以是本题的点重构。总之就是解决一个范围的问题，也就是满足某一条件的点在树上有特定的范围（比如子树）。

虚树

莫队

普通莫队

概述

例题

P10149 [Ynoi1999] XM66F

推式子。

考虑莫队，现在就是考虑怎么维护增量，对于当前区间 \([l,r]\)：

• 假设往右边拓展：\([l,r+1]\)，那么贡献为 \(\Delta= \sum_{i=l}^r [a_i=a_{r+1}]\times (\sum_{j=1}^r[a_j<a_{r+1}]-\sum_{j=1}^{i-1}[a_j<a_{r+1}])\)
• 假设往左边拓展：\([l-1,r]\)，那么贡献为 \(\Delta= \sum_{i=l}^r [a_i=a_{l-1}]\times (\sum_{j=1}^{i-1}[a_j<a_{l-1}]-\sum_{j=1}^{l-2}[a_j<a_{l-1}])\)

两者贡献可以合并，对于 \(p = l-1\) 或 $p=r+1 $，有贡献 \(\Delta=\sum_{i=l}^r[a_i=a_p]\times |\sum_{j=1}^{i-1}[a_j<a_p]-\sum_{j=1}^{p-1}[a_j<a_p]|\)

直接预处理出 \(pre_i=\sum_{j=1}^{i-1}[a_j<a_i]\) 即可，删除同理。

时间复杂度：\(\mathcal O(n\sqrt{m})\)。

回滚莫队/不删除莫队

待修莫队

二维莫队/高维莫队

二离莫队

树上莫队

莫队配合 bitset

KD-Tree

分块

序列分块/普通分块

例题

P5048 [Ynoi2019 模拟赛] Yuno loves sqrt technology III

考虑分块。值得注意的是，本题空限只有 62.50MB。

先离散化，然后预处理 \(f_{i,j}\) 表示第 \(i \sim j\) 块的众数出现次数。时间复杂度：\(\mathcal O(n\sqrt{n})\)，空间复杂度：\(\mathcal O(n)\)。

用 vector 存储每个数值所有元素的出现位置。再记录每个元素在相应 vector 里的下标 \(p_i\)。空间复杂度：\(\mathcal O(n)\)。

考虑询问，整块直接使用预处理出的 \(f_{i,j}\) 的值即可，记当前答案 \(ans=f_{i,j}\)。

再考虑散块的影响，由于散块的贡献最多只有 \(2\sqrt{n}\)，我们只需检查这些散块元素，每次判断这些数的出现次数能否达到 \(ans+1\)。

对于左边的散块元素 \(x\)，我们在相应的 vector 里找到下标为 \(p_x+ans\) 的元素 \(y\)，若 \(y\le r\)，则说明该数值在范围内至少有 \(ans+1\) 个数，暴力更新 \(ans\leftarrow ans+1\) 即可。

对于右边的散块元素 \(x\)，我们在相应的 vector 里找到下标为 \(p_x-ans\) 的元素 \(y\)，若 \(y\ge l\)，则说明该数值在范围内至少有 \(ans+1\) 个数，暴力更新 \(ans\leftarrow ans+1\) 即可。

时间复杂度：\(\mathcal O((n+m)\sqrt{n})\)，空间复杂度 \(\mathcal O(n)\)。

操作序列分块/时间分块

操作分块 - kymru - 博客园

分块优化算法-CSDN博客

算法

现在序列长度为 \(n\)，有 \(m\) 个操作。

如果操作数量较少，我们可以把操作记下来，在询问的时候加上这些操作的影响。

假设最多记录 \(T\) 个操作，则修改为 \(\mathcal O(1)\)，询问 \(\mathcal O(T)\)。

\(T\) 个操作时候，重新计算前缀和，\(\mathcal O(n)\)。

总复杂度：\(\mathcal O(mT+n\frac{m}{T})\)。

\(T=\sqrt{n}\) 时，总复杂度 \(\mathcal O(m\sqrt{n})\)。

例题

P2137 Gty的妹子树

考虑只有询问的操作。

则用 dfs 序+主席树直接做。

时间复杂度：\(\mathcal O(n\log n)\)

考虑有修改怎么做：那么回答每一个询问就相当于把初始答案与每一操作带来的影响结合起来。

具体地，考虑一个操作怎么影响一个询问：

1. 当操作为第一个类型时，它能够影响一个询问 \(x\)，当且仅当修改在 \(x\) 的子树内。
2. 当操作为第二个类型时，它能够影响一个询问 \(x\)，当且仅当它新建在 \(x\) 的子树内。

先用一个数据结构维护初始状态，接着对于每一个询问，扫一次它前面所有的修改操作，如果发现能够影响答案，那就将答案改变。肯定过不了，考虑优化。

考虑操作序列分块，转为需要实现的操作只剩为两个了：

1. 需要一个数据结构维护区间 \([l,r]\) 一个数 \(x\) 的区间rank。（用来维护 \(\sqrt{m}\) 个操作以前的答案，就相当于序列分块的整块答案）
2. 判断一个点是否在另一个点的子树中。（用来维护 \(\sqrt{m}\) 个操作以后的答案，就相当于序列分块的散块答案）

看到1我们想到主席树，2因为有修改，可以用倍增。

时间 ：\(\mathcal O(n\times \log n \times \sqrt{m})\)，能过。

重构时间复杂度：主席树重构时间复杂度为 \(\mathcal O(n\times \log n)\)，一共暴力重构 \(\sqrt{m}\) 次，时间复杂度为 \(\mathcal O(n\times \log n \times \sqrt{m})\)。

询问时间复杂度：由于对于每一个询问操作我们需要往前扫 \(\sqrt{m}\) 个修改并且每个修改花 \(\mathcal O(\log n)\) 的时间暴力倍增，就相当于序列分块的散块暴力查询，最后我们还要加上前面整块的答案，也就是用主席树维护的那一部分。时间复杂度为：\(\mathcal O(m\times (\log n\times \sqrt{m}+\log n))\)。

值域分块

二维分块

bitset

例题

P11731 [集训队互测 2015] 最大异或和

一个性质（小 Trick），对于一个序列 \(a_1,a_2,\dots,a_n\)，它的线性基和 \(a_1,a_2 \oplus a_1,a_3 \oplus a_2,\dots,a_n \oplus a_{n-1}\) 的线性基是一样的。

考虑证明：发现 \(a_2=a_1 \oplus (a_2 \oplus a_1),a_3=a_2 \oplus (a_3 \oplus a_2),\dots,a_n=a_{n-1}\oplus (a_n \oplus a_{n-1})\)，即原序列中任意一个元素都可以被表示出来，那么原数组能表示的数，差分数组也能表示出来，原因显然。

那么考虑现在怎么做，转为异或差分序列后，操作一就相当于是单点异或，操作二就是区间赋值为 \(0\)。每次最多只改变两个原来为 \(0\) 的位置，所以最多只能有 \(n+q\) 次让一个数变为 \(0\)，现在需要一个能支持带删除的线性基。对于每个数维护一个删除时间，用 bitset 维护位运算之类的操作即可。

时间复杂度：因为一次位运算操作为 \(\frac{m}{w}\)，线性基一共要进行 \(m\) 次操作，所以一次插入操作时间复杂度为 \(\mathcal O(\frac{m^2}{w})\)，每个数总共被拆为了 \(\mathcal O(n+q)\) 个区间，所以总复杂度为 \(\mathcal O(\frac{nm^2}{w})\)。

代码：

int n,m,q,op,l,r;
int pre[N];
vector<pair<bitset<M>,int> > g[N];
bitset<M> a[N],d[N],x,t;
pair<bitset<M>,int >p[M];
bool f[N];
struct Linear_basis{
	void ins(pair<bitset<M>,int> x)
	{
		for(int i=m-1;i>=0;i--)
		{
			if(x.fi[i]==0)continue;
			if(p[i].sd==-1)
			{
				p[i]=x;
				return;
			}
			if(p[i].sd<x.sd)swap(p[i],x);
			x.fi^=p[i].fi;
		}
	}
	bitset<M> qmax()
	{
		bitset<M> ans;
		for(int i=m-1;i>=0;i--)if(!ans[i]&&p[i].sd!=-1)ans^=p[i].fi;
		return ans;
	}
	inline void print(bitset<M> ans){
		for(int i = m - 1; i >= 0; --i)
	  		putchar(ans[i] + '0');
		putchar('\n');
	}
}G;
void solve()
{
	cin>>n>>m>>q;
	for(int i=1;i<=n;i++)cin>>a[i],d[i]=a[i-1]^a[i];
	for(int i=1;i<=q;i++)
	{
		cin>>op;
		if(op==1)
		{
			cin>>l>>r>>x;
			for(int j=l;j<=r;j++)a[j]^=x;
		}
		if(op==2)
		{
			cin>>l>>r>>x;
			for(int j=l;j<=r;j++)a[j]=x;
		}
		if(op==3)f[i]=1;
		if(op<=2)
		{
			for(int j=l;j<=min(r+1,n);j++)
			{
				t=a[j-1]^a[j];
				if(t!=d[j])
				{
					if(d[j].count())g[pre[j]].pb(mk(d[j],i));
					d[j]=t;
					pre[j]=i;
				}
			}
		}
	}
	for(int i=1;i<=n;i++)if(d[i].count())g[pre[i]].pb(mk(d[i],q+1));
	for(int j=0;j<=m;j++)p[j].sd=-1;
	for(int i=0;i<=q;i++)
	{
		for(int j=0;j<=m;j++)if(p[j].sd==i)p[j].sd=-1;
		for(auto t:g[i])G.ins(t);
		if(f[i])G.print(G.qmax());
	}
}

SP30738 ADACOINS - Ada and Coins

bitset 优化01背包，时间复杂度为 \(\mathcal O(\frac{n^2}{w})\)。

P1537 弹珠

基本上算是双倍经验？

7715 -- 【10.19模拟】无向图

考虑DP，设 \(f_{i,j,s}\) 表示从 \(i\) 到 \(j\) 是否有一条状态为 \(s\) 的连边。

那么显然时间复杂度是：\(Θ(s^d×n×(n+m))\) 的。

考虑第一个优化，使用 bitset，我们能够优化掉jj那一维。

但是时间复杂度还是不够，于是我们考虑 meet in the middle 算法，只算前一半即可。

时间复杂度：\(Θ(2^{\frac{d}{2}}×n×(n+m)+2^d×n)\)。

8217 -- 【11.05-NOIP模拟】旅行

bitset 优化传递闭包。

时间复杂度：\(\mathcal O(\frac{Dn^3}{w})\)。

珂朵莉树

概述

例题

P9995 [Ynoi2000] rspcn

我们可以感性理解区间排序同区间覆盖一样，原数组任何时候都是一段一段有序或者无序的划分，每次操作可以是合并也可以是分裂，故也可以用珂朵莉树维护。

每一段用线段树维护即可，其中线段树需支持分裂和合并。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

链剖分

重链剖分

概述

例题

1518 -- 【BZOJ4127】Abs

诈骗题。

注意到 \(0\le d,|a_i| \le 10^8\)，说明每个 \(a_i\) 从负数变为正数只需执行一次。那么我们重链剖分时，线段树记一下当前区间中的小于 \(0\) 的那些数的绝对值的最小值（如果没有则为 \(0\)），每次点权加 \(d\) 的时候只要遇到区间里没有负数或者负数的绝对值的最小值大于 \(d\) 的区间就直接执行懒标记更新的操作，不必再进行递归修改，其余情况则继续修改即可。

现在考虑加操作对答案的影响：肯定就是区间中正数个数乘上 \(d\) 再减去区间中负数个数乘上 \(d\)。原因显然。（针对直接更改区间懒标记的情况）

现在考虑计算时间复杂度：因为最多 \(n\) 次从负数变为正数，每次更改都需经过 \(\log n\) 个线段树上面的节点，所以总复杂度为：\(\mathcal O(n \log n)\)。

CF916E Jamie and Tree

Solution

如果没有换根操作，那么我们只需要对这棵树的 \(\texttt{DFS}\) 序建立线段树，支持区间修改和区间查询。

接下来考虑换根操作。此时我们显然不能真的把根换掉，根只能一直为 \(1\) 节点，而是要对根和操作的节点的关系进行分类讨论！

由于操作 \(2\) 和操作 \(3\) 在位置关系分析上的本质是相同的，所以我们只需要考虑位置关系和如何求 LCA 即可。

位置关系

设当前整棵树的根节点为 \(R\)，询问的子树根节点为 \(X\)，那么我们可以发现这两者存在以下 \(3\) 种关系。

对于每种位置关系的图示，\(R\) 和 \(X\) 均标记在节点上，蓝色的节点表示需要被操作的节点。

1. 如果 \(R\) 就是 \(X\)：

   此时整棵树的所有节点都需要被操作。

2. 如果 \(R\) 不在 \(X\) 的子树内：

   此时我们可以发现 \(X\) 这棵子树的形态与原图的形态一致，所以只要对以 \(1\) 为根节点时的子树 \(X\) 进行操作即可。

3. 如果 \(R\) 位于 \(X\) 的子树内：

   此时情况比较复杂，需要被操作的节点为： 所有节点除去以 \(X\) 到 \(R\) 的路径上的第一个节点（这个点满足既是 \(R\) 的祖先，又是 \(X\) 的儿子）为根的子树。那么我们可以根据容斥原理，先对整棵树进行操作，再对那个子树进行相反的操作（如果是查询则减去贡献，如果是修改则减去）。

   那么怎么求这个点呢？我们记 \(deep_i\) 表示 \(i\) 在原图中的深度，让 \(R\) 往上移动 \(deep_R-deep_X-1\) 个点即可，这个过程显然可以用倍增实现。

如何求 LCA

其实也是之前的分类讨论的套路啦！QAQ

设当前整棵树的根节点为 \(r\)，修改的节点为 \(x,y\)。在以 \(1\) 为根节点的前提下，我们也可以分类讨论！（以下内容参考 \(\texttt{Codeforces}\) 官方题解）

1. 如果 \(x,y\) 都在 \(r\) 的子树内，那么 \(\texttt{LCA}\) 显然为 \(\texttt{LCA}(x,y)\)。
2. 如果 \(x,y\) 只有一个在 \(r\) 的子树内，那么 \(\texttt{LCA}\) 肯定为 \(r\)。
3. 如果 \(x,y\) 都不在 \(r\) 的子树内，我们可以先找到 \(p=\texttt{LCA}(x,r)\)，\(q=\texttt{LCA}(y,r)\)。如果 \(p\) 和 \(q\) 不相同，那么我们选择其中较深的一个；如果 \(p\) 和 \(q\) 相同，那么 \(\texttt{LCA}\) 就是 \(x,y\) 的 \(\texttt{LCA}\)。

综上所述，我们可以发现我们要求的 \(\texttt{LCA}\) 就是 \(\texttt{LCA}(x,y)\)，\(\texttt{LCA}(x,r)\)，\(\texttt{LCA}(y,r)\) 这三者中深度最大的！

时间复杂度：\(O(n\log n)\)。

4303 -- 【FJOI2010集训】最小生成树

典题。

分类讨论：

• 当这条边本来就不在最小生成树上，那么答案就是最小生成树的边权权值和。
• 当这条边在最小生成树上，我们使用重链剖分/倍增预处理出这条边的替代边即可。

时间复杂度：\(\mathcal O(n \log n)\)。

P7671 [GDOI2016] 疯狂动物城

\[\sum\limits_{i \in x\rightarrow y}\!{a_i}\times\dfrac{\operatorname{dis}(i,y)(\operatorname{dis}(i,y)+1)}{2} \]

在这里，我们发现了一个很熟悉的部分，\(\operatorname{dis}(i,y)\)。

像这样的树上两点距离，肯定是要无脑的给他拆成 \(dep_i+dep_y-2\times dep_{\operatorname{LCA}(i,y)}\)。

然后把这部分拆开看看，再把 \(\dfrac{1}{2}\) 提到前面去，就得到了：

\[\dfrac{1}{2}\sum\limits_{i \in x\rightarrow y}\!{a_i}\times(dep_i+dep_y-2\times dep_{\operatorname{LCA}(i,y)})(dep_i+dep_y-2dep_{\operatorname{LCA}(i,y)}+1) \]

欸，这式子怎么越化越复杂了，难道要全部拆开吗？

显然不是的，我们发现这里的 \(\operatorname{dis}(i,y)\) 有一个与其他推式子题不一样的特性，就是其中的 \(y\) 点是已经给定的。

又因为 \(i\) 是 \(x\rightarrow y\) 路径上的点，所以当 \(i\) 是 \(\operatorname{LCA}(x,y)\rightarrow x\) 的那一段时，\(\operatorname{LCA}(i,y)\) 就是 \(\operatorname{LCA}(x,y)\)。

同理的考虑当 \(i\) 是 \(\operatorname{LCA}(x,y)\rightarrow y\) 的那一段时，\(\operatorname{LCA}(i,y)\) 就是 \(i\)。

这下式子就有着美妙的性质了，再考虑下按照这两个部分给他化开。

下面式子中用 \(lca\) 表示 \(\operatorname{LCA}(x,y)\)。

1. 当 \(i\in lca\rightarrow x\) 时，式子即为：

\[\dfrac{1}{2}\sum\limits_{i\in lca\rightarrow x}\!{a_i}\times(dep_i+dep_y-2dep_{lca})(dep_i+dep_y-2dep_{lca}+1) \]

观察到 \(dep_y-2\times dep_{lca}\) 是个定值，直接用 \(s_1\) 来表示他，就得到了：

\[\dfrac{1}{2}\sum\limits_{i\in lca\rightarrow x}\!{a_i}\times(dep_i+s_1)(dep_i+s_1+1) \]

再接一步大力展开：

\[\dfrac{1}{2}\sum\limits_{i\in lca\rightarrow x}\!{a_i}\times((dep_i+s_1)^2+(dep_i+s_1)) \]

\[\dfrac{1}{2}\sum\limits_{i\in lca\rightarrow x}\!{a_i}\times(dep_i^2+2s_1dep_i+s_1^2+dep_i+s_1) \]

最后把求和也给展开，就得到了：

\[\dfrac{1}{2}\left[\sum\limits_{i\in lca\rightarrow x}{a_idep_i^2}+\sum\limits_{i\in lca\rightarrow x}{a_idep_i\left(2s_1+1\right)}+\sum\limits_{i\in lca\rightarrow x}{a_i\left(s_1^2+s_1\right)}\right] \]

2. 当 \(i\in lca\rightarrow y\) 时，式子即为：

\[\dfrac{1}{2}\sum\limits_{i\in lca\rightarrow y}\!{a_i}\times(dep_i+dep_y-2dep_i)(dep_i+dep_y-2dep_i+1) \]

\[\dfrac{1}{2}\sum\limits_{i\in lca\rightarrow y}\!{a_i}\times(dep_y-dep_i)(dep_y-dep_i+1) \]

发现其中的 \(dep_y\) 为不变量，用 \(s_2\) 代入展开得：

\[\dfrac{1}{2}\sum\limits_{i\in lca\rightarrow y}\!{a_i}\times(s_2^2-2dep_is_2+dep_i^2+s_2-dep_i) \]

最后再展开下求和就得到了：

\[\dfrac{1}{2}\left[\sum\limits_{i\in lca\rightarrow y}{a_idep_i^2}-\sum\limits_{i\in lca\rightarrow y}{a_idep_i\left(2s_2+1\right)}+\sum\limits_{i\in lca\rightarrow y}{a_i\left(s_2^2+s_2\right)}\right] \]

至此，最艰难的一步就完成了。

然后再去看题面中其他的部分，因为有版本回溯，所以直接大力上一颗主席树。

对于链加，直接标记永久化即可。

主席树上维护三个值，分别是正常的点权和，乘上 \(dep\) 的点权合和乘上 \(dep^2\) 的点权和。

但是，这题我们需要完成主席树上的区间修改、区间查询，因为主席树的不同版本节点时存在共用的，如果我们随意地 pushdown 以及 pushup 的话就会得到错误答案，因此我们每次修改都需要新建节点，这会导致空间非常大，其中有大量冗余节点。因此，我们可以使用标记永久化的方法，在修改时，如果节点区间被完全包含了，直接将懒标记打到节点上再返回，有交集就累加上更改的值然后向其遍历；在查询时，一路累加懒标记的贡献，同样在节点区间被完全包含时返回。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

6385 -- 【11.08题目】三只企鹅

Solution 1：点分树

建立出点分树后转化为询问 \(x\) 的所有点分祖先的点分子树的信息。然后随便用容斥搞一搞就行了。

Solution 2：重链剖分

不难发现，题目要求出的实际是：\(\sum_{u=1}^n cnt_u \times dis(u,x)\)。

把 \(dis\) 拆开可得：

\[\sum_{u=1}^n cnt_u \times (dep_u+dep_x-2\times dep_{\text{lca}}) \]

然后我们发现 \(cnt_u\times dep_u,cnt_u\times dep_x\)，都可以修改时直接求出。

难点在于怎么求出 \(cnt_u\times 2\times dep_{\text{lca}}\)。

其实这就很套路了，我们每次修改的时候，将 \(x\) 到根的路径全部加上对应点的 \(dep\) 值即可，查询就相当于是询问 \(x\) 到祖先链上的值即可。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

P4211 [LNOI2014] LCA

重链剖分（离线）

注意到询问可以差分，即答案可以表示为 \(\sum_{i=1}^r dep[\text{LCA}(i,z)]-\sum_{i=l}^{l-1}dep[\text{LCA}(i,z)]\)。

那么问题转化为前缀求解答案，考虑扫描线。

对于当前扫到的这个点 \(i\)，我们把 \(i\) 到根节点的路径上的所有点 \(u\) 都加上 \(w(fa[u],u)\)，其中 \((u,v)\) 表示 \(u,v\) 之间的边权，此题为 \(1\)。

要在线的话，就使用主席树差分一下就行了。

P5305 [GXOI/GZOI2019] 旧词

此题要求 \(\sum_{i\le x}dep[\text{LCA}(i,y)]^k\)，那么我们就把 \(w(u,v)\) 设为 \((dep[u]-dep[v])^k\) 就行了。

实链剖分/LCT

概述

例题

6517 -- 【2020.5.9模拟】数颜色

根据【Tricks】里面记载，树上连通块等于点数减去边数。于是我们令点的贡献为 \(1\)，边的贡献为 \(-1\)，所求即为最后的权值和。

再回到原问题上，我们要求的是 \([l_i,r_i]\) 之间的路径点数和边数并，并集问题考虑扫描线降颜色一维，维护变化量。因为点和边的计算方式差不多，这里以点的计算方式为例。我们记 \(last_u\) 表示 \(u\) 按照颜色这一维扫描线后最后的颜色，那么每次我们询问是否 \(last_u\in [l_i,r_i]\) 即可。类似【树点涂色】那道题，每拿到一个新颜色，我们就在旧颜色减去贡献，在新颜色加上贡献即可。也就是 \(\text{access}\) 的时候，我们在打通实链的同时，减去旧颜色贡献，加上新颜色贡献即可，查询时计算每个颜色的贡献即可，用 BIT 快速维护。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

关键代码

int access(int x,int i)
{
	int child;
	for(child=0;x;child=x,x=fa[x])
	{
		splay(x);
		ch[x][1]=0;pushup(x);
		if(tag[x])bt.update(tag[x],-sum[x]);
		tag[x]=i;bt.update(tag[x],sum[x]);
		ch[x][1]=child;pushup(x);
	}
	return child;
}

SP16549 QTREE6 - Query on a tree VI

题意就是要维护同色连通块大小。要用LCT维护子树大小就不说了。

这是一种高级的维护染色连通块的较为通用的模型。

很多与树有关的题目，当边权不好处理时，有时候会转化为此边子节点的点权处理。因为有根树中除了根，每个点都有唯一的父边。

请仔细品味上面这句话。

在这一题里，道理是一样的，但转化方向却是反的，要把点化为边！

把每个点的父边赋予该点的颜色。我们需要两个LCT，每种对应一个颜色。一条边只有在对应颜色的LCT中才会被连上。

于是，原来同色点的连通块，就变成了剪开顶端节点后的边的连通块（解释一下，因为点的颜色给了父边，那么既然是顶端节点，那它的父边就不会在连通块中，也就是这个点与连通块不同色，于是该点的所有子树不能连起来，于是要剪掉）

然后就可以惊讶地发现，修改一个点的颜色之后，只要在原来颜色对应LCT中断掉父边，再在新颜色对应LCT中连接父边，就可以轻而易举地维护连通块啦。

再谈查询，上面提到了要剪开顶端节点（也就是连通块构成的树的树根），于是先findroot，再输出它的重子树的大小。

一个小细节，1节点是没有父亲的，不过为了模型的建立，要有父边，于是需要加一个虚点，让1的父亲指向它连边。

#include<cstdio>
#include<cstdlib>
#define R register int
#define I inline void
const int N=1000009,M=N<<1;
#define lc c[x][0]
#define rc c[x][1]
#define C col[u]
int fa[N],he[N],ne[M],to[M];
bool col[N];
struct LCT{
	int f[N],c[N][2],si[N],s[N];
	bool r[N];
	LCT(){for(R i=1;i<N;++i)s[i]=1;}//注意初始化
	inline bool nroot(R x){return c[f[x]][0]==x||c[f[x]][1]==x;}
	I pushup(R x){
		s[x]=s[lc]+s[rc]+si[x]+1;
	}
	I rotate(R x){
		R y=f[x],z=f[y],k=c[y][1]==x,w=c[x][!k];
		if(nroot(y))c[z][c[z][1]==y]=x;c[x][!k]=y;c[y][k]=w;
		f[w]=y;f[y]=x;f[x]=z;
		pushup(y);
	}
	I splay(R x){
		R y;
		while(nroot(x)){
			if(nroot(y=f[x]))rotate((c[f[y]][0]==y)^(c[y][0]==x)?x:y);
			rotate(x);
		}
		pushup(x);
	}
	I access(R x){
		for(R y=0;x;x=f[y=x]){
			splay(x);
			si[x]+=s[rc];
			si[x]-=s[rc=y];
		}
	}
	inline int findroot(R x){
		access(x);splay(x);
		while(lc)x=lc;
		splay(x);
		return x;
	}
	I link(R x){//只传一个参数，因为只会连父边，cut同理
		access(x);splay(x);
		R y=f[x]=fa[x];
		access(y);splay(y);//与常规LCT不同，别忘加
		si[y]+=s[x];s[y]+=s[x];
	}
	I cut(R x){
		access(x);splay(x);
		lc=f[lc]=0;
		pushup(x);
	}
}lct[2];
void dfs(R x){
	for(R y,i=he[x];i;i=ne[i])
		if((y=to[i])!=fa[x])
			fa[y]=x,dfs(y),lct[0].link(y);
}
#define G ch=getchar()
#define in(z) G;\
	while(ch<'-')G;\
	z=ch&15;G;\
	while(ch>'-')z*=10,z+=ch&15,G
int main(){
	register char ch;
	R p=1,n,m,i,u,v,op;
	in(n);
	for(i=1;i<n;++i){
		in(u);in(v);
		to[++p]=v;ne[p]=he[u];he[u]=p;
		to[++p]=u;ne[p]=he[v];he[v]=p;
	}
	dfs(1);
	fa[1]=n+1;lct[0].link(1);//虚点
	in(m);
	while(m--){
		in(op);in(u);
		if(op)lct[C].cut(u),lct[C^=1].link(u);
		else{
			v=lct[C].findroot(u);
			printf("%d\n",lct[C].s[lct[C].c[v][1]]);
		}
	}
    return 0;
}

P3348 [ZJOI2016] 大森林

1.思路

1.所有修改和查询都离线处理，双关键字排序，第一关键字：位置，第二关键字：操作顺序（严格保证修改在查询前）。

2.本题 makeroot 会破坏父子关系，所以我们 link 操作时无法使用 makeroot 。证明及操作在下面。

3.对于每次 0 操作，我们记录下左右端点， 1 操作要更改时可以直接获得包含此节点的区间，并把新建节点与最近的虚节点 link 。

4.对于每次 1 操作，我们采用类似于差分的思路，我们建一个虚节点，并把修改拆成两次操作。

• 4.1：遍历到 \(l\) 时，将新建虚节点（包含后面的新建节点）与要修改的生长节点 link ，从而达到把 \(l - r\) 的以后的 0 操作都在要修改的生长节点之下的目的。

• 4.2：遍历到 \(r+1\) 时， \(r+1 - n\) 与此操作无关，所以需要把新建虚节点与上一个虚节点 link 从而达到 \(r+1 - n\) 不受此操作影响的目的。

不懂换生长节点操作的可以看下面的图， 4 操作就是 图1 - 图2 - 图1

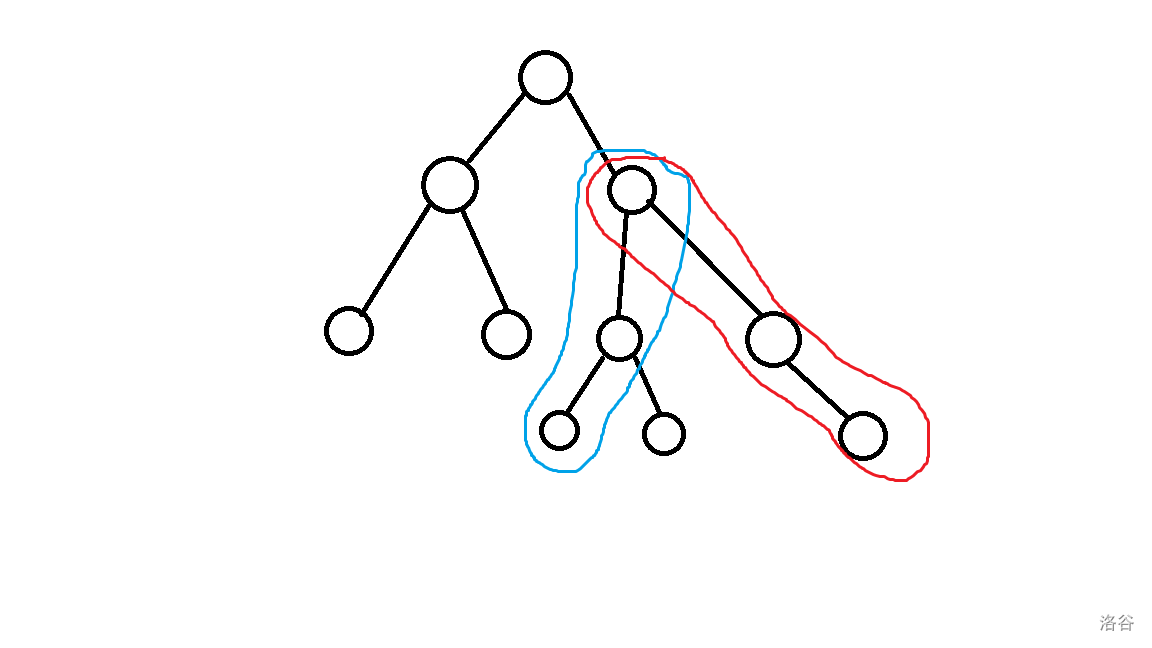
5.对于每次 2 操作，我们直接在 LCT 上求 lca ，然后树上差分求距离（\(dis(x,y) = dep[x] + dep[y] - 2 \times dep[lca]\)），

如图， access(x) 后 access(y) 的最后一次到达链上的节点即为 lca ，因为 access(x) 后 \(x\) 的所有祖先节点都在链上，

access(y) 最后一次到达链上的节点即为 \(x\) 和 \(y\) 的公共祖先且为最近公共祖先。 \(dep[x]\) 就是 access(x) , splay(x) 的子树大小，因为链上的都是祖先节点。

2.无 makeroot 的 link 的正确性证明

很多题解都没有说为什么 link 前可以直接 splay ,然后我想了一下发现 splay 都不用……本题中 link 有两种情况，第一种是 1 和 2 操作中的新建节点，毫无疑问是根，第二种是 sort 后的修改，在 link 前已经 cut 了，此时此节点必为根。

void link(int x,int y)
{
  a[x].fa=y;
}

长链剖分

概述

例题

P4292 [WC2010] 重建计划

长剖做法。

首先最外层肯定要套一个二分（分数规划）。

然后考虑怎么check，考虑DP，设 \(f_{u,j}\) 表示从 \(u\) 的子树的点到 \(u\) 的距离为 \(j\)，最大的权值和。

那么我们有转移：\(f_{u',j}=f_{u,k}\times f_{v,j-k}(k\le j)\)。但是直接转移是 \(\mathcal O(n^2)\)，但是注意到DP方程中的一维状态与深度有关，考虑用长链剖分将其优化至更优的复杂度。

首先长链直接继承信息，考虑短链怎么处理，首先肯定可以暴力合并，但是问题是如何更新答案。

首先明确一点，我们肯定是可以在边暴力合并短链时边计算答案的，对于当前的节点 \(u\)，答案更新肯定是所有点对 \((p,q)\)，以 \(u\) 为 \(\text{LCA}\) 来更新答案。然后发现答案更新是由一个子树与其它子树之间的贡献。这个贡献可以具体的表示为从 \(a\) 的子树中选择一条长度为 \(x\) 的路径，再在 \(b\) 的子树中选择一条长度为 \(y\) 的路径。满足 \(L\le x+y \le R\)，更新的权值为 \(dis_{p \in \text{subtree}(a)}+dis_{q \in \text{subtree}(b)}-2\times dis_u\)，因为我们再合并过程中枚举短链合并，顺带着枚举了一维 \(p\)，那么所有能更新答案的 \(q\) 一定在一个深度区间上，且一定是到 \(u\) 的权值和最大的。

那么，用形式化描写出我们现在的问题。问题即为，一个点有两个属性 \(dep,dis\)，我们要询问有多少个点满足它在 \(u\) 的子树中（\(q\in \text{subtree}(u)\)），然后深度在 \(dep_u+[\min(1,L-(dep_p-dep_u)),\max(R-(dep_p-dep_u),maxdep_u-dep_u)]\) 之间，且 \(dis\)（权值和最大）的点 \(q\)。发现这是一个二维偏序问题，先考虑能不能降维，\(q\in \text{subtree}(u)\) 可以用一个小技巧规避掉，我们在合并短链时把顺便把所有点的深度信息向长链合并，这样我们只用查找长链的信息就可以了。至此可以用线段树维护一个区间的最值即可，查询就在线段树所维护的那个长链查询即可。

最后不要忘了，\(u\) 和 \(u\) 子树中的节点产生的贡献还是要计算的。

时间复杂度：二分一个 \(\log\)，线段树维护区间最值一个 \(\log\)，所以总体上复杂度为 \(\mathcal O(n \log^2 n)\)。

可以看代码获得更好的理解。

const int N=2e5+50;
const double eps=1e-6,inf=100000000000000.0;
int n,L,R,tot;
int head[N],cnt,sonw[N],son[N],len[N],dep[N],mxdep[N],dfn[N];
int num[N*2];
double sonw2[N],ans,dis[N],last[N],maxx[N*2];
struct edge{
	int to,nxt,w;
	double w2;
}e[N*2];
void add(int u,int v,int w)
{
	e[++cnt].to=v;
	e[cnt].nxt=head[u];
	e[cnt].w=w;
	head[u]=cnt;
}
void dfs(int u,int fa)
{
	mxdep[u]=dep[u]=dep[fa]+1;
	for(int i=head[u];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==fa)continue;
		dfs(v,u);
		if(mxdep[u]<mxdep[v])
		{
			mxdep[u]=mxdep[v];
			son[u]=v;
			sonw[u]=e[i].w;
		}
	}
	len[u]=mxdep[u]-dep[u]+1;
}
void dfs2(int u,int fa)
{
	dfn[u]=++tot;
	if(son[u])dfs2(son[u],u);
	for(int i=head[u];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==fa||v==son[u])continue;
		dfs2(v,u);
	}
}
void build(int p,int l,int r)
{
	if(l==r)
	{
		num[l]=p;
		return;
	}
	int mid=(l+r)>>1;
	build(p*2,l,mid);build(p*2+1,mid+1,r);
}
void clear(int p,int l,int r)
{
	maxx[p]=-inf;
	if(l==r)return;
	int mid=(l+r)>>1;
	clear(p*2,l,mid);clear(p*2+1,mid+1,r);
}
double query(int p,int l,int r,int x,int y)
{
	if(x<=l&&r<=y)return maxx[p];
	int mid=(l+r)>>1;
	double res=-inf;
	if(x<=mid)res=max(res,query(p*2,l,mid,x,y));
	if(y>mid)res=max(res,query(p*2+1,mid+1,r,x,y));
	return res;
}
void update(int p,int l,int r,int x,double k)
{
	maxx[p]=max(maxx[p],k);
	if(l==r)return;
	int mid=(l+r)>>1;
	if(x<=mid)update(p*2,l,mid,x,k);
	else update(p*2+1,mid+1,r,x,k);
}
void solve(int u,int fa)
{
	update(1,1,n,dfn[u],dis[u]);
	if(son[u])
	{
		dis[son[u]]=dis[u]+sonw2[u];
		solve(son[u],u);
	}
	for(int i=head[u];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==fa||son[u]==v)continue;
		dis[v]=dis[u]+e[i].w2;
		solve(v,u);
		for(int j=1;j<=len[v];j++)
		{
			last[j]=maxx[num[dfn[v]+j-1]];
			if(j<=R)
			{
				int ql=max(1ll,dfn[u]+L-j),qr=min(dfn[u]+R-j,dfn[u]+mxdep[u]-dep[u]);
				double tmp=query(1,1,n,ql,qr);
				ans=max(ans,tmp+last[j]-2*dis[u]);
			}
		}
		for(int j=1;j<=len[v];j++)update(1,1,n,dfn[u]+j,last[j]);
	}
	ans=max(ans,query(1,1,n,dfn[u]+L,min(dfn[u]+R,dfn[u]+mxdep[u]-dep[u]))-dis[u]);
}
bool check(double x)
{
	ans=-inf;
	for(int i=1;i<=cnt;i++)e[i].w2=1.0*e[i].w-x;
	for(int i=1;i<=n;i++)sonw2[i]=sonw[i]*1.0-x;
	clear(1,1,n);
	solve(1,0);
	return ans>=0;
}
signed main()
{
	scanf("%lld %lld %lld",&n,&L,&R);
	for(int i=1;i<=n-1;i++)
	{
		int u,v,w;
		scanf("%lld %lld %lld",&u,&v,&w);
		add(u,v,w);add(v,u,w);
	}
	dfs(1,0);
	dfs2(1,0);
	build(1,1,n);
	double l=0,r=1000000000;
	while(r-l>eps)
	{
		double mid=(l+r)/2;
		if(check(mid))l=mid;
		else r=mid;
	}
	printf("%.3lf\n",l);
	return 0;
}

#33. 【UR #2】树上GCD

！：首先观察 \(\sum_{i=1}^n [\gcd(x,y)=i]\)，是不好直接求解的，我们考虑倍数容斥一下，即求解 \(\sum_{i=1}^n [i|\gcd(x,y)]\) 的值，最后减去不合法的即可。

我们考虑枚举 \(x,y\) 的 \(lca\)，然后再 \(lca\) 处求解，记 \(cnt_{u,d}\) 表示\(u\) 子树中到 \(u\) 的距离为 \(d\) 的点的个数。由于距离与深度有关，考虑长链剖分。

长链剖分时，我们只需考虑两条链的合并过程即可。设两条链为 \(u,v\)，长度为 \(len_u,len_v\) 且 \(len_u \ge len_v\)。称 \(u\) 为长链，\(v\) 为短链。

显然贡献只会产生在 \(i \le len_v\) 中，那么我们可以枚举 \(i\in[1,len_v]\)，问题转化为求解 \(\sum [i|x]\times [i|y]\)。但是不能直接枚举长链，现在问题在于不能对长链 \(u\) 暴力计算。

仍然是套路，不妨考虑对 \(i\) 进行根号分治。显然 \(i>\sqrt{n}\) 的部分，暴力在 \(cnt[u]\) 上跳 \(i\) 的倍数，复杂度是可以接受的 \(\mathcal O(n\sqrt{n})\)。而对于 \(i≤\sqrt{n}\)，由于数量较少，则考虑直接维护。只需对于每个 \(i\)，分别计算一遍，维护出 \(siz[u]\) 表示 \(u\) 的子树中距离 \(u\) 为 \(i\) 的倍数的数量，可以通过 \(u\) 向 \(u\) 的 \(i\) 级祖先更新以快速地维护。显然这部分的复杂度也是 \(\mathcal O(n\sqrt{n})\) 的，完全可以接受。

最后考虑一种特殊情况，即对于 \(u\) 是 \(v\) 的祖先的部分，由于在启发式合并时可能会交换 \(cnt[u]\) 与 \(cnt[v]\)，故这种情况的贡献不能在合并过程中统计。但是也很好维护，因为注意到所有深度 \(≥i\) 的点（深度指到根的距离）都会对 \(Ans[i]\) 造成 \(1\) 的贡献，所以只需要在输出答案时加上即可。

综上，整个程序的复杂度为 \(\mathcal O(n \sqrt{n})\)。

6308 -- 【10.06模拟】树

Solution 1：点分树

建立出点分树后转化为询问 \(x\) 的所有点分祖先的点分子树的信息。口胡的，感觉时间复杂度是 \(\mathcal O(n\log n)\)。因为点分祖先只有 \(\mathcal O(\log n)\) 个，再因为询问需要容斥，也就是我们要算出所有点分祖先到 \(x\) 的距离，和每个点分祖先的父亲到 \(x\) 的距离，这个好像可以 \(\mathcal O(1)\) 询问两点祖先并回答，但是如果想偷懒的话 \(\mathcal O(\log n)\) 的时间求解 \(\texttt{lca}\) 的话，时间复杂度就是 \(\mathcal O(n \log^2 n)\)。

本做法的优势在于与 \(k\) 大小无关。

Solution 2：长链剖分

基于 \(k\) 大小的做法，因为 \(k\) 只有 \(400\)，所以我们暴力爬父亲，把一个询问拆为 \(k\) 个询问，每个询问就是询问 \(u\) 这个点到 \(u\) 子树中距离为 \(k-dis(u,x)\) 的点的个数，注意这个东西还是需要容斥。长链剖分 \(\mathcal O(n)\) 处理即可。

注意这里长剖 \(f_{u,i}\) 维护的是在 \(u\) 子树里的点到 \(u\) 的距离大于等于 \(i\) 的权值和。这样才好维护一点。

时间复杂度：瓶颈在于 \(k\)，因为有 \(\mathcal O(qk)\) 个询问，所以时间复杂度就是 \(\mathcal O(qk)\)。

#284. 快乐游戏鸡

UOJ #284. 快乐游戏鸡题解（长链剖分+单调栈合并） - Fighoh - 博客园

可持久化数据结构

操作树

概述

例题

P5391 [Cnoi2019] 青染之心

设 \(n\) 是物品数量，\(m\) 是背包容量，\(Q\) 是操作次数。

不难发现其实就是按照 dfs 序给出了一棵树，树上每一个点 \(x\) 都有一个权值为 \(v_x\)，重量为 \(w_x\) 的物品，然后把每一个节点到根的路径上的物品拎出来求完全背包。

首先最坏情况就是一条链，时间复杂度显然是 \(O(Qn)\) 的，但是我们空间并没办法承受 \(O(nm)\) 的复杂度，所以这道题瓶颈在于优化空间。

考虑重链剖分，每一条重链只开一个 dp 数组，因为每一个点到根节点上重链是 \(O(\log n)\) 的，所以这样空间是 \(O(m\log n)\) 的。

假设我们 dfs 到了点 \(x\)，\(x\) 位于它到根上第 \(\text{dep}\) 条重链，我们先遍历其所有轻儿子 \(y\)，用 \(f[\text{dep}][0\sim m]\) 更新 \(f[\text{dep+1}][0\sim m]\)，然后继续 dfs 节点 \(y\)。

回溯回来后 \(x\) 子树内就只有 \(x\) 的重儿子为根的子树没有被 dp 过了，此时也就意味着可以直接在 \(f[\text{dep}][0\sim m]\) 中加入 \(x\) 重儿子的贡献了。

时间复杂度 \(O(Qn)\)，空间复杂度 \(O(m\log n)\)。

可将其理解为操作树上重链剖分。

AT_abc165_f [ABC165F] LIS on Tree

板子，建出树后，我们使用线段树维护最长上升子序列长度。同时支持撤销操作就行了。

时间复杂度：\(\mathcal O(n \log n)\)。

CF707D Persistent Bookcase

根据题意建立出操作树，维护数组 \(s_i\) 表示 \(i\) 这一行中有多少个 \(1\)，\(rev_i\) 表示这一行的状态，\(ans\) 表示到当前节点的答案，\(a_{i,j}\) 表示 \((i,j)\) 的值。

• 当操作为 \(3\) 时，直接更改 \(rev_i \leftarrow rev_{i} \oplus 1\)，\(s_i=m-s_i\)，\(ans \leftarrow ans-s_i-(m-s_i)\)。

• 当操作为 \(1\) 时：

  • 当当前所在行的状态为 \(1\) 且 \(a_{i,j}=1\) 时，表明实际上 \((i,j)\) 的值为 \(0\)，这时置一操作有效，更改为 \(s_i\leftarrow s_i+1\)，\(ans \leftarrow ans+1\)，\(a_{i,j}=0\)。
  • 当当前所在行的状态为 \(1\) 且 \(a_{i,j}=0\) 时，表明实际上 \((i,j)\) 的值为 \(1\)，这时置一操作无效，更改为 \(s_i\leftarrow s_i\)，\(ans \leftarrow ans\)，\(a_{i,j}=0\)。
  • 当当前所在行的状态为 \(0\) 且 \(a_{i,j}=0\) 时，表明实际上 \((i,j)\) 的值为 \(0\)，这时置一操作有效，更改为 \(s_i\leftarrow s_i+1\)，\(ans \leftarrow ans+1\)，\(a_{i,j}=1\)。
  • 当当前所在行的状态为 \(0\) 且 \(a_{i,j}=1\) 时，表明实际上 \((i,j)\) 的值为 \(1\)，这时置一操作无效，更改为 \(s_i\leftarrow s_i\)，\(ans \leftarrow ans\)，\(a_{i,j}=1\)。

• 当操作为 \(2\) 时：

  • 当当前所在行的状态为 \(1\) 且 \(a_{i,j}=1\) 时，表明实际上 \((i,j)\) 的值为 \(0\)，这时置零操作无效，更改为 \(s_i\leftarrow s_i\)，\(ans \leftarrow ans\)，\(a_{i,j}=1\)。
  • 当当前所在行的状态为 \(1\) 且 \(a_{i,j}=0\) 时，表明实际上 \((i,j)\) 的值为 \(1\)，这时置零操作有效， 更改为 \(s_i\leftarrow s_i+1\)，\(ans \leftarrow ans+1\)，\(a_{i,j}=1\)。
  • 当当前所在行的状态为 \(0\) 且 \(a_{i,j}=0\) 时，表明实际上 \((i,j)\) 的值为 \(0\)，这时置零操作无效，更改为 \(s_i\leftarrow s_i\)，\(ans \leftarrow ans\)，\(a_{i,j}=0\)。
  • 当当前所在行的状态为 \(0\) 且 \(a_{i,j}=1\) 时，表明实际上 \((i,j)\) 的值为 \(1\)，这时置零操作有效， 更改为 \(s_i\leftarrow s_i+1\)，\(ans \leftarrow ans+1\)，\(a_{i,j}=0\)。

时间复杂度：\(\mathcal O(Q)\)。

P4810 [COCI 2014/2015 #3] STOGOVI

可持久化类的题目。

可持久化的题显然不能将每种状态都记录下来，可以考虑将所有状态集中到一棵树上，每个分支可以看作不同状态的延伸。这样做的好处是每次新增状态的本质就是原树节点或原树节点的简单延伸。

回归本题，使用树的方法做达到可持久化的效果：

我们维护每个栈栈顶的元素 \(top_i\)，对于 \(a\) 操作，即原树新增节点，且父亲节点为 \(top_v\)；

对于 \(b\) 操作 ，直接将 \(top_i\) 赋值为 \(top_v\) 的父节点即可；

对于c操作，先令 \(top_i=top_v\)，由于每个元素互不相同且树只会向下简单延伸的性质，两栈相同数的个数即为 \(top_i\) 与 \(top_w\) 节点的 LCA 深度，倍增维护即可。

时间复杂度：\(\mathcal O(n \log n)\)。

可持久化栈

概述

同样的，我们记录栈顶，即 \(root_i=top\)。但是要支持出栈操作，那么我们就记录 \(top\) 下一个是谁即可，记录为 \(pre_{root_i}=root_{i-1}\)，弹栈操作就直接跳到 \(pre\) 即可。

代码：

struct PersistentStack{
	int tp,stk[N],root[N],pre[N];
	inline void push(int p,int x)
	{
		stk[++tp]=x;
		root[p]=tp;
		pre[root[p]]=root[p-1];
	}
	inline void update(int p,int x){root[p]=root[x];}
	inline void pop(int p){root[p]=pre[root[p-1]];}
	inline int top(int p){return stk[root[p]];}
	bool empty(int p)
	{
		if(root[p]==0)return true;
		return false;
	}
}S;

例题

6735 -- 【模板】可持久化栈

板子。

AT_abc273_e [ABC273E] Notebook

板子。

可持久化数组

概述

同理，用可持久化线段树维护数组就行。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+50;
int n,m,a[N],tot,root[N];
struct Persistent_SegmentTree{
	struct node{
		int l,r,val;
	}T[23*N];
	int clone(int p)
	{
		T[++tot]=T[p];
		return tot;
	}
	int build(int p,int l,int r)
	{
		p=++tot;
		if(l==r)
		{
			T[p].val=a[l];
			return tot;
		}
		int mid=(l+r)>>1;
		T[p].l=build(T[p].l,l,mid);
		T[p].r=build(T[p].r,mid+1,r);
		return p;
	}
	int update(int p,int l,int r,int x,int y)
	{
		int newp=clone(p);
		if(l==r)
		{
			T[newp].val=y;
			return newp;
		}
		int mid=(l+r)>>1;
		if(x<=mid)T[newp].l=update(T[newp].l,l,mid,x,y);
		if(x>mid)T[newp].r=update(T[newp].r,mid+1,r,x,y);
		return newp;
	}
	int query(int p,int l,int r,int x)
	{
		if(l==r)return T[p].val;
		int mid=(l+r)>>1;
		if(x<=mid)return query(T[p].l,l,mid,x);
		if(x>mid)return query(T[p].r,mid+1,r,x);
	}
}T;
int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	root[0]=T.build(0,1,n);
	for(int i=1;i<=m;i++)
	{
		int v,op,x,y;
		scanf("%d %d %d",&op,&v,&x);
		if(op==1)
		{
			scanf("%d",&y);
			root[i]=T.update(root[v],1,n,x,y);
		}
		else if(op==2)
		{
			printf("%d\n",T.query(root[v],1,n,x));
			root[i]=root[v];
		}
	}
	return 0;
}

例题

6733 -- 【模板】可持久化数组

板子。

双倍经验：P3919 【模板】可持久化线段树 1（可持久化数组）

6734 -- 【模板】可持久化并查集

用可持久化数组维护并查集合并的过程即可。

具体的：

相比与之前的并查集，我们多出了返回之前版本的操作。

那么版本和版本之间的根本差别就是 \(\text{fa}\) 数组。

我们考虑对 \(\text{fa}\) 数组进行可持久化，具体的，我们在开始操作前建立一棵可持久化线段树。

线段数的叶子 \([l,l]\) 表示的是编号为 \(l\) 的数的父亲。

但是这样是不够的。考虑原本的并查集的 \(\text{find}\) 函数。

int find(int now)
{
	if(fa[now]==now)return now;
	reutrn fa[now]=find(fa[now]);
}

我们知道，平常时候使用的并查集优化是路径压缩，查询复杂度是均摊 \(O(n\alpha)\) 的。

但是均摊并不可以，因为我们无法保证某次查询复杂度不为 \(O(n)\)，这样对于可持久化来说是毁灭性的，如果你操作一次为 \(O(n)\)，那么我们可能会被要求返回这个版本，再次进行这种不讲武德的操作。

所以我们要寻找一种 \(\text{find}\) 方式，使得我们的复杂度为单次严格 \(O(\log n)\) 的。

这时候，按秩合并就出现了，他就有单次 \(O(\log n)\) 的优美复杂度，还是严格的。

具体的，按秩合并有多重方式，

1. 按照深度

2. 按照大小

3. 随机

好的我们考虑前两个因为第3个被卡掉了

这里只讲深度，因为比较好理解，一次查询的复杂度应该为 \(u\to root\) 的距离，虽然这是棵树，但是不能保证邪恶的出题人不会给我们一条链子。

• 按照深度：我们不但记录某个点的 \(\text{fa}\) 还需要记录这个点的子树的深度 \(\text{dep}\)。

对于一次操作合并 \(u,v\)。

我们让 \(u=\text{find}(u),v=\text{find}(v)\)。

考虑把两者合并起来（假定 \(\color{red}{\text{dep}_u\ge \text{dep}_v}\)）

我们显然应该把 \(v\) 的子树合并到 \(u\) 的下面。

只有这样才能保证深度尽可能的小。

我们考虑 \(\text{dep}_u\) 变成了什么？

• 如果 \(\text{dep}_u=\text{dep}_v\)，那么我们把 \(v\) 放到 \(u\) 的下方，\(\text{dep}_v\) 增大了 \(1\)。由于 \(\text{dep}_u\) 表示的是以 \(u\) 为根节点的深度所以 \(\text{dep}_u=\text{dep}_v+1\)

• 如果 \(\text{dep}_u>\text{dep}_v\) 深度不变。

如果按这样合并的顺序的话，全部合并完，我们的树高最大也只有 \(\log n\)。

所以复杂度为严格单次 \(O(\log n)\)。

那么具体的，对于一次修改，我们需要新建 \(\color{red}\text{2}\) 个版本。

首先将这个版本中的 \(\text{fa}_v\) 变为 \(u\)，接着，我们需要修改 \(\text{dep}_u\)。

这个过程中新建立了两个版本！！！！

不能贪心的在修改 \(\text{dep}_u\) 的时候直接在原本的版本上修改。

如果这样的话你会获得 \(88\text{pts}\) 的好成绩。

上代码~

ps.复杂度还是很可以的，不开O2依然很稳。

如果你不是很懂为什么需要建立两个版本可以看这里：

首先我们需要明确新建的两个版本是什么。

1. 将 \(\text{fa}_v\) 变成 \(u\) 这一步很好理解，没有什么问题。

2. 将 \(\text{dep}_u\) 更新，这里很重要，一定要新建一个版本来更新 \(\text{dep}_u\) 否则会复杂度错误。

如果你不新建版本而是直接修改 \(\text{dep}_u\) ，那么假如当前版本是 \(now\)，我们知道 \(now\) 这个版本是 \(now-1\) 版本修改 \(\text{fa}_v\) （即 1. ） 产生的，因此 \(now\) 和 \(now-1\) 所对应的 \(\text{dep}_u\) 实际上是同一个数组。

如果你在 \(now\) 版本直接修改了 \(\text{dep}_u\) 那么意味着 \(now-1\) 版本的 \(\text{dep}_u\) 同时被修改了，那么这时候，我们的 \(\text{dep}\) 数组就有可能不满足按秩合并的优美性质了，此时如果数据让我们回溯到 \(now-1\) 版本修改，那么可能就会导致按秩合并出错，从而导致复杂度错误。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

可持久化线段树

概述

例题

SP11470 TTM - To the moon

题意概括一下就是区间修改的可持久化线段树。

一般的可持久化线段树都是单点改的，这道题肯定不能一个一个改。想想普通线段树的区间修改，是找到最多 \(\log n\) 个节点并打上懒标记。这样我们当然可以也找到这 \(\log n\) 个节点并继承。但是标记一下传就会出问题：某两个版本的线段树共用的节点不能修改值，如果直接新建节点下传标记的化那么空间和时间就会爆掉。

于是用标记永久化。标记永久化既不需要下传标记，也不需要通过子节点更新自己。

具体来说：对被修改区间覆盖的节点打上标记，其左右子节点继承上个版本的左右子节点。

放图来看：

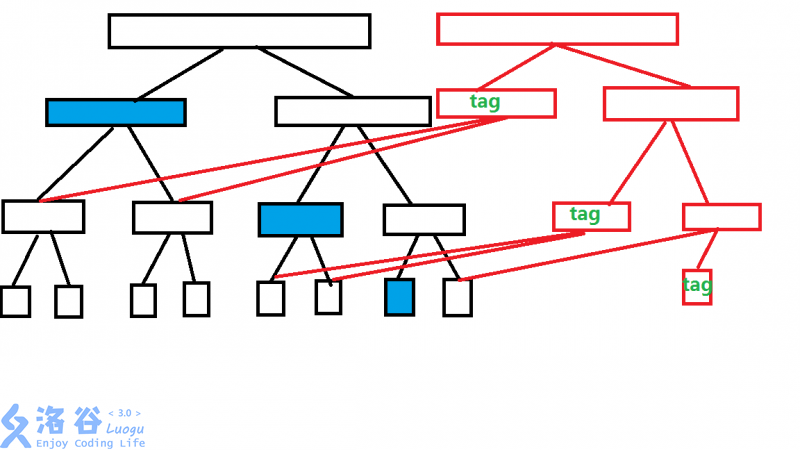
就会发现，查询时红色线段树有标记，查询时 \(tag\) 会对答案产生影响， \(tag\) 不下放就不会影响到两棵线段树的公共节点，就能保证不会互相影响了。

时间复杂度：\(O(n\log n)\)。

空间复杂度：每个区间最多被分成 \(2\log n\) 个节点，所以为 \(O(n\log n)\)。

1489 -- 【BZOJ4504】K个串kstring

首先看到 \(k\) 很小，考虑 \(k\) 路归并。

考虑扫描线定一求一，定 \(r\)，看所有 \(l\) 与 \(r\) 组成的区间即可。于是我们要对于任意一个区间快速求出 \([l,r]\) 的权值，因为是求区间种类数，所以对于左端点在 \([pre_{a_i},i]\) 的点，我们在 \(i\) 处加上贡献，也就是说扫描线解决 \(r\) 一维，可持久化线段树维护所有 \(r\) 的 \(l\) 权值即可。

直接类似超级钢琴一样 \(k\) 路归并即可。

时间复杂度：\(\mathcal O(n \log n)\)。

7953 -- 【5.18NOI测试】浑水摸鱼

应该是第一次遇见 \(\mathcal O(n \log^3 n)\) 的算法？

本题其实就是求另类的本质不同的子串个数。

考虑如果是一般的本质不同怎么做呢，弄一个后缀数组，然后height之和就是重复的个数。

这题其实也差不多，只不过排序的 cmp 有点复杂。

考虑如果我们可以把每个后缀用最小表示出来，然后进行排序，答案为 \(\frac{n×(n+1)}{2}−\sum LCP(str_i,str_{i+1})\) 。

考虑把 hash 表示成 \(\sum (next_i−i)×p^i\) ，其中 \(next_i\) 为和 \(i\) 相同的数的下一个位置，如果没有的话就设为 \(i\) ，那两个最小表示的串相同的话 hash 就可以体现其相同。

考虑用主席树维护子串的 hash 值，然后排序时二分 hash 即可。

时间复杂度：\(\mathcal O(n \log^3 n)\)。

代码：

#include <bits/stdc++.h>
#define LL long long
#define U unsigned long long
using namespace std;
const int N=5e4+5,M=2e6+5;
const U B=793999;
int n,a[N],ls[M],rs[M],T[N],t,p[N],nx[N];
LL ans; U s[M],b[N]; set<int>S[N];
#define mid ((l+r)>>1)
void upd(int &x,int y,int l,int r,int v,U w){
	x=++t;s[x]=s[y]+w;
	ls[x]=ls[y];rs[x]=rs[y];
	if (l==r) return;
	if (mid>=v) upd(ls[x],ls[y],l,mid,v,w);
	else upd(rs[x],rs[y],mid+1,r,v,w);
}
U qry(int x,int l,int r,int L,int R){
	if (L<=l && r<=R) return s[x];
	if (mid>=R) return (ls[x]?qry(ls[x],l,mid,L,R):0);
	if (mid<L) return (rs[x]?qry(rs[x],mid+1,r,L,R):0);
	return (ls[x]?qry(ls[x],l,mid,L,R):0)+(rs[x]?qry(rs[x],mid+1,r,L,R):0);
}
U hs(int l,int r){return (T[l]?qry(T[l],1,n,l,r):0);}
int lcp(int x,int y){
	int l=0,r=n-max(x,y)+1;
	while(l<r){
		int i=(l+r+1)>>1;
		if (hs(x,x+i-1)*b[x]==hs(y,y+i-1)*b[y]) l=i;
		else r=i-1;
	}
	return l;
}
int Pos(int x,int i){
	return (*S[a[i]].lower_bound(x))-x;
}
bool cmp(int x,int y){
	int l=lcp(x,y);
	if (x+l>n) return 1;if (y+l>n) return 0;
	return Pos(x,x+l)<Pos(y,y+l);
}
int main(){
	cin>>n;b[0]=1;
	for (int i=1;i<=n;i++)
		scanf("%d",&a[i]),b[i]=b[i-1]*B,
		p[i]=i,S[a[i]].insert(i);
	for (int i=n;i;i--){
		T[i]=T[i+1];
		if (nx[a[i]]) upd(T[i],T[i],1,n,
			nx[a[i]],b[n-i+1]*(nx[a[i]]-i));
		nx[a[i]]=i;
	}
	stable_sort(p+1,p+n+1,cmp);ans=1ll*n*(n+1)/2;
	for (int i=1;i<n;i++) ans-=lcp(p[i],p[i+1]);
	printf("%lld\n",ans);return 0;
}

P2839 [国家集训队] middle

根据【Tricks】里记载，中位数可以有二分转为 \(-1,1\) 序列后进行判定。

那么我们二分出一个值 \(mid\)，把小于它的设为 \(-1\)，大于等于它的设为 \(1\)。

\([a, b]\) 求一个最大后缀子段和，\([c, d]\) 求一个最大前缀子段和，\([b+1, c-1]\) 求一个和。

加起来如果大于等于 \(0\)，那么满足要求，且这个数还可以变大，否则就只能缩小。

每个数开一个线段树来做，空间开不下，用主席树即可。

具体的，先每个数排个序扫描线维护变化量即可。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

可持久化Trie

概述

例题

P6088 [JSOI2015] 字符串树

注意到输入所有字符串长度不超过 \(10\)，也就是说可以暴力在 trie 上面查询。

考虑树上差分（因为有可加性），用可持久化 trie 支持即可。

3889 -- 【省选模拟1】Kpm的MC密码

考虑把所有字符串都给倒过来处理，求 \(k\) 小可以二分，用可持久化 trie 即可。

4445 -- 【FJMTC2015#4】神牛的养成计划

数据范围看漏了……

首先直接对输入的字符串按字典序排序，然后先把它们按照前缀的方式一个一个插入到 trie 里面，这样查询 \(s_1\) 时对应到第一棵 trie 树上的那个结点所管辖的区间就是一段连续的编号。我们找到连续的编号以后，就使用可持久化 trie 去反串查分查找 \(s_2\) 即可。

时间复杂度：\(\mathcal O(\text{len} \log \text{len})\)，即瓶颈在排序。

6730 -- 【模板】最大异或和--可持久化01-trie

可持久化 01-trie 板子。

1729 -- 【BZOJ2741】L序列

可持久化 trie 树+分块

把区间异或和转化为前缀相异或的形式，问题就转化为：在 \([l−1,r]\) 中选出 \(i\) 和 \(j\) ，使得 \(sum_i \oplus sum_j\) 最大。

如果确定一个端点，另一个端点在某区间内的话，可以使用可持久化 trie 树来解决。

本题两个端点都是只有区间范围限制。考虑分块，预处理出 \(f_{x,y}\) 表示从第 \(x\) 块到第 \(y\) 块的答案。然后对于询问，整块直接取出答案，零碎的部分再使用可持久化 trie 树暴力即可。

时间复杂度：\(\mathcal O(n\sqrt{n}\log n)\)。

SP11444 MAXOR - MAXOR

双倍经验。

1340 -- 【BZOJ4260】异或REBXOR

01-trie 的基本应用，也就是前面扫一遍，后面扫一遍就行了，不是到为什么 jzp 要把它放在可持久化里面。

3875 -- 【HDU4757】Tree

01-trie 的基本应用，同样的发现本题可以差分做，用可持久化 trie 差分就行了，类似与线段树上二分的思想。

P5795 [THUSC 2015] 异或运算

注意到 \(n\) 很小只有 \(1000\)，\(p\) 也很小，只有 \(500\)，我们对 \(m\) 这一维度建立可持久化 01-trie，然后二分答案。我们对 \(n\) 在 \(m\) 的 trie 上多树二分就行了。

时间复杂度：\(\mathcal O(m \log v+np \log v)\)。

P4098 [HEOI2013] ALO

\(\mathtt{Algorithm}\)：

• ST 表 + 二分 + 可持久化 Trie。

\(\mathtt{Solution}\)：

• 首先，思考 \(a_i\) 会在哪些区间作为次大值。设 \(l_1\) 表示 \(i\) 左边第一个比 \(a_i\) 大的数的下标（没有就是 \(0\)），设 \(l_2\) 表示 \(i\) 左边第二个比 \(a_i\) 大的数的下标（没有就是 \(0\)）。\(r_1\)（没有就是 \(n+1\)）表示 \(i\) 右边第一个比 \(a_i\) 大的数的小标，\(r_2\)（没有就是 \(n+1\)）同理。

• 显然，\(a_i\) 就只有在 \([l_1+1,r_2-1]\) 或 \([l_2+1,r_1-1]\) 时是次大值。这时，我们就可以在 Trie 上贪心地求出最大值。

• 而对于 \(l_1\) 和 \(l_2\) 的求法，我们可以二分。更具体地，首先我们二分出 \(l_1\) 的位置，再在此基础上二分出 \(l_2\) 的位置，\(r_1\) 和 \(r_2\) 同理。

• 查询区间 \([l,r]\) 与一个数的异或极值可以用可持久化 01-trie 来维护。

可持久化平衡树

概述

例题

P3835 【模板】可持久化平衡树

因为每次 merge 和 split 的时间复杂度是 \(\mathcal O(\log n)\) 的，也就是说我们每次进行这两个操作的时候最多访问 \(\log n\) 个节点。那么我们就可以进行可持久化了，每次进行 merge 和 split 的时候就顺便新建节点继承信息即可。

时间复杂度：\(\mathcal O(n \log n)\)，空间复杂度：\(\mathcal O(n \log n)\)。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+50;
random_device Rd;
mt19937 Gen(Rd());
int rd(int l,int r){return uniform_int_distribution<int> (l,r)(Gen);}
int n,tot,xx,yy,zz,root[N];
struct node{
	int ch[2],sz,pri,w;
}t[N*50];
void pushup(int p)
{
	t[p].sz=1;
	if(t[p].ch[0])t[p].sz+=t[t[p].ch[0]].sz;
	if(t[p].ch[1])t[p].sz+=t[t[p].ch[1]].sz;
}
int clone(int w)
{
	t[++tot].w=w;
	t[tot].sz=1;
	t[tot].pri=rd(1,1000000);
	return tot;
}
int merge(int x,int y)
{
	if(!x||!y)return x+y;
	if(t[x].pri<t[y].pri)
	{
		int rt=clone(0);
		t[rt]=t[x];
		t[rt].ch[1]=merge(t[rt].ch[1],y);
		pushup(rt);
		return rt;
	}
	else
	{
		int rt=clone(0);
		t[rt]=t[y];
		t[rt].ch[0]=merge(x,t[rt].ch[0]);
		pushup(rt);
		return rt;
	}
}
void split(int rt,int k,int &x,int &y)
{
	if(!rt)x=0,y=0;
	else
	{
		if(t[rt].w<=k)
		{
			x=clone(0);
			t[x]=t[rt];
			split(t[x].ch[1],k,t[x].ch[1],y);
			pushup(x);
		}
		else
		{
			y=clone(0);
			t[y]=t[rt];
			split(t[y].ch[0],k,x,t[y].ch[0]);
			pushup(y);
		}
	}
}
int findkth(int rt,int k)
{
	while(1)
	{
		if(k<=t[t[rt].ch[0]].sz)
			rt=t[rt].ch[0];
		else
		{
			if(t[rt].ch[0])k-=t[t[rt].ch[0]].sz;
			if(!--k)return rt;
			rt=t[rt].ch[1];
		}
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1,tmp,op,a;i<=n;i++)
	{
		xx=yy=zz=0;
		scanf("%d %d %d",&tmp,&op,&a);
		root[i]=root[tmp];
		if(op==1)
		{
			split(root[i],a,xx,yy);
			root[i]=merge(merge(xx,clone(a)),yy);
		}
		else if(op==2)
		{
			split(root[i],a,xx,zz);
			split(xx,a-1,xx,yy);
			yy=merge(t[yy].ch[0],t[yy].ch[1]);
			root[i]=merge(merge(xx,yy),zz);
		}
		else if(op==3)
		{
			split(root[i],a-1,xx,yy);
			printf("%d\n",t[xx].sz+1);
			root[i]=merge(xx,yy);
		}
		else if(op==4)
		{
			printf("%d\n",t[findkth(root[i],a)].w);
		}
		else if(op==5)
		{
			split(root[i],a-1,xx,yy);
			if(xx==0)
			{
				printf("-2147483647\n");
				continue;
			}
			printf("%d\n",t[findkth(xx,t[xx].sz)].w);
			root[i]=merge(xx,yy);
		}
		else if(op==6)
		{
			split(root[i],a,xx,yy);
			if(yy==0)
			{
				printf("2147483647\n");
				continue;
			}
			printf("%d\n",t[findkth(yy,1)].w);
			root[i]=merge(xx,yy);
		}
	}
	return 0;
}

P5055 【模板】可持久化文艺平衡树

同上题，只不过我们这题要打标记，而又因为需要可持久化，所以 pushdown 时必须新建节点。

时间复杂度：\(\mathcal O(n \log n)\)，空间复杂度：\(\mathcal O(n \log n)\)。

UVA12538 自带版本控制功能的IDE Version Controlled IDE

板子题。

Dsu On Tree

概述

例题

CF601D Acyclic Organic Compounds

题目要求一个点 \(v\) 到其子树内的点 \(S_v\) 构成的本质不同字符串数量。可以给每个串的前面都加一段从根到 \(v\) 父节点的前缀，不影响答案。此时一个点对应了从根到该点的字符串。

直接用哈希维护每个点对应的串，原问题就转变为子树内颜色数，可以通过 dfs 序变为区间颜色数。直接上树状数组维护即可。

时间复杂度：\(\mathcal O(n\log n)\)。

分治部分

整体二分

猫树分治

子区间分治树——猫树分治。

猫树特点&作用

如果只需要进行 \(\textcolor{red}{静态子区间查询}\)，那么可以在 \(\textcolor{red}{完美二叉树}\) 上 \(\textcolor{red}{预处理所有区间前后缀信息}\) 进行 \(\textcolor{red}{快速合并}\)。

注意：当然离不离线都可以，由于其过程类似于点分治，所以在线的情况可通过类似于建出建出点分治的情况动态维护。

简单来讲，线段树能维护的信息猫树基本都能维护。
比如什么区间和、区间 gcd 、最大子段和 等 满足结合律且支持快速合并的信息

算法流程

猫树分治的大致思想有点像整体二分，又有点像分治求满足 xxx 条件的区间个数的思想。

如果一个区间 \([L,R]\) 包含整个 \([l,r]\) 区间，且 \(l,r\) 分别位于这个区间 $mid=\left \lfloor \frac{L+R}{2} \right \rfloor $ 左右两侧，那么通过左右子节点内部的前后缀信息+答案信息，即可合并得到子区间信息。

不强制在线

设当前递归分治下去的区间为 \([L,R]\)，\(mid\) 为 $\left \lfloor \frac{L+R}{2} \right \rfloor $。分治到这个区间的询问序列为 \(Q\)，\(Q_{i}\) 表示一个二元组 \((l,r)\)。预处理出 \(suf_i(i \in [L,mid])\) 和 \(pre_i \in [mid+1,R]\) 分别表示 \([i,mid]\) 的后缀信息和 \([mid+1,R]\) 的前缀信息，后面根据情况合并，因为这样猫树需要 \(\textcolor{red}{要求维护的信息可合并}\)。
再定义两个 vector \(L_q\) 和 \(R_q\)。递归函数为 \(\operatorname{solve}(L,R,Q)\)。

按照区间包含关系分类讨论：

依次遍历询问序列 \(Q\) 的每一个元素。对于当前询问 \(Q_{i}\) 的二元组 \((l,r)\)。

• 当 \([l,r] \subseteq [L,mid]\) 时，将 \(Q_i\) 压入 vector \(L_q\) 中。
• 当 \([l,r] \subseteq [mid+1,R]\) 时，将 \(Q_i\) 压入 vector \(R_q\) 中。
• 当 \(l \in [L,mid],R \in [mid+1,R]\) 时，将 \(suf_l\) 和 \(pre_r\) 进行合并即可。

最后调用 \(\operatorname{solve}(L,mid,L_q)\) 和 \(\operatorname{solve}(mid+1,R,R_q)\)即可。

设插入的时间复杂度为 \(T_{\text{insert}}(n)\)，查询时信息之间合并复杂度为 \(T_{\text{merge}}(n)\)，则根据主定理有：

\(\mathcal O(n\log n·T_{\text{insert}}(n)+q·T_{\text{merge}}(n))\)。

为了看清楚猫树分治的优势，我们对比一下其它数据结构的复杂度（前提是假设都能做）。

线段树：\(\mathcal O(n\log n·T_{\text{merge}}(n)+q\log n·T_{\text{merge}}(n))\)。

看到没有，当 \(T_{\text{merge}}(n)\) 的复杂度过于高时，就不能使用线段树了。

强制在线

直接对于每一层分治记录下 \([i,mid],[mid+1,j]\) 的答案，这样可以做到强制在线，复杂度：\(n\log n·T_{\text{insert}}(n)+q\log n+q·T_{\text{merge}}(n)\)，当然这样空间可能略有点危，如果记我们单个合并的信息的空间复杂度为 \(M(n)\)，那么该做法空间复杂度为 \(n\log n·M(n)\)。

例题

P6240 好吃的题目

模板题，上述过程中的结构换成背包即可，这样往背包中加入一个元素复杂度为 \(\mathcal O(V)\)，合并两个背包复杂度也是 \(\mathcal O(V)\)，总复杂度就是 \(n\log n·V+qV\) 可以通过此题。

#include<bits/stdc++.h>
using namespace std;
const int N=4e4+50,M=205,Q=2e5+50;
int n,m;
int h[N],w[N],ans[Q],L[N][M],R[N][M];
struct ques{
	int l,r,t,id;
}q[Q],b[Q];
void solve(int l,int r,int x,int y)
{
	if(x>y)return;
	int mid=(l+r)>>1;
	memset(L[mid+1],0,sizeof(L[mid+1]));memset(R[mid],0,sizeof(R[mid])); 
	for(int i=mid;i>=l;i--)
	{
		for(int j=0;j<=200;j++)
		{
			L[i][j]=max(j?L[i][j-1]:0,L[i+1][j]);
			if(j>=h[i])L[i][j]=max(L[i][j],L[i+1][j-h[i]]+w[i]);
		}
	}
	for(int i=mid+1;i<=r;i++)
	{
		for(int j=0;j<=200;j++)
		{
			R[i][j]=max(j?R[i][j-1]:0,R[i-1][j]);
			if(j>=h[i])R[i][j]=max(R[i][j],R[i-1][j-h[i]]+w[i]);
		}
	}
	int ql=x,qr=y;
	for(int i=ql;i<=qr;i++)b[i]=q[i];
	for(int i=x;i<=y;i++)
	{
		if(b[i].r<mid)q[ql++]=b[i];
		else if(b[i].l>mid)q[qr--]=b[i];
		else
		{
			int res=0;
			for(int j=0;j<=b[i].t;j++)res=max(res,L[b[i].l][j]+R[b[i].r][b[i].t-j]);
			ans[b[i].id]=res;
		}
	}
	solve(l,mid,x,ql-1);solve(mid+1,r,qr+1,y);
}
int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++)scanf("%d",&h[i]);
	for(int i=1;i<=n;i++)scanf("%d",&w[i]);
	for(int i=1;i<=m;i++)scanf("%d %d %d",&q[i].l,&q[i].r,&q[i].t),q[i].id=i;
	solve(1,n,1,m);
	for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
	return 0;
}

P3246 [HNOI2016] 序列

由于本题没有修改，所以三种解法，一种离线，两种在线。

Algorithm1 莫队：

莫队本质是维护变化量，但是此题看上去并不好维护。

当 \([l,r]\) 拓展至 \([l,r+1]\) 时，\(\Delta ans=\sum_{i=l}^{r+1} \min_{j=i}^{r+1} a_j\) 。考虑交换求和符号，并且设 \(pre_i\) 表示从 \(i\) 开始向左第一个小于 \(a_i\) 的位置 \(pos\)。 \(f[l][r]\) 表示固定 \(r\) 左端点在 \([l,r]\) 的贡献：\(f[l][r]=\sum_{i=l}^{r} \min_{j=i}^{r} a_j\)。根据 \(f[l][r]\) 的定义，有递推式：

\(f[l][r]=f[l][pre_r]+(r-pre_r)\times a_r\)。

现在考虑怎么表示出 \(\Delta ans\)，还需另 \(p\) 表示 \([l,r+1]\) 之间最小值的下标。则 \(\Delta ans = (p-l+1)\times a_p+f[p+1][r+1]\)。

发现增量只与 \(r\) 有关，考虑差分去掉 \(l\) 这一维。具体地，另 \(g_r=g_{pre_r}+(r-pre_r)\times a_r\)。则有 \(f[l][r]=g_r-g_{l-1}\)，注意此时此式成立必须要满足 \(g_{l-1}\) 最后能递推到 \(g_r\)。

时间复杂度：\(\mathcal O(n\sqrt{n})\)。

#include<bits/stdc++.h>
#define fp(i,a,b) for(register int i=a,I=b+1;i<I;++i)
#define fd(i,a,b) for(register int i=a,I=b-1;i>I;--i)
#define go(u) for(register int i=fi[u],v=e[i].to;i;v=e[i=e[i].nx].to)
#define file(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
char ss[1<<17],*A=ss,*B=ss;
inline char gc(){return A==B&&(B=(A=ss)+fread(ss,1,1<<17,stdin),A==B)?-1:*A++;}
template<class T>inline void sd(T&x){
    char c;T y=1;while(c=gc(),(c<48||57<c)&&c!=-1)if(c==45)y=-1;x=c-48;
    while(c=gc(),47<c&&c<58)x=x*10+c-48;x*=y;
}
char sr[1<<21],z[20];int C=-1,Z;
inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;}
template<class T>inline void we(T x){
    if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x;
    while(z[++Z]=x%10+48,x/=10);
    while(sr[++C]=z[Z],--Z);sr[++C]='\n';
}
const int N=1e5+5,inf=2e9;
typedef int arr[N];
typedef long long ll;
struct Q{
    int l,r,x,id;
    inline bool operator<(const Q b)const{return x==b.x?x&1?r<b.r:r>b.r:x<b.x;}
}q[N];
int n,m,Sz,Top,Mi[17],f[N][17];arr a,pre,suf,S,Log;ll Now,fl[N],fr[N],ans[N];
inline int cmp(const int x,const int y){return a[x]<a[y]?x:y;}
inline int qry(int L,int R){int t=Log[R-L+1];return cmp(f[L][t],f[R-Mi[t]+1][t]);}
inline ll left(int L,int R){int p=qry(L-1,R);return (ll)a[p]*(R-p+1)+fl[L-1]-fl[p];}
inline ll right(int L,int R){int p=qry(L,R+1);return (ll)a[p]*(p-L+1)+fr[R+1]-fr[p];}
int main(){
    #ifndef ONLINE_JUDGE
        file("s");
    #endif
    sd(n);sd(m);Sz=sqrt(n);a[n+1]=a[0]=inf;
    Mi[0]=1;fp(i,1,16)Mi[i]=Mi[i-1]<<1;
    fp(i,2,n)Log[i]=Log[i>>1]+1;
    fp(i,1,n)sd(a[i]),f[i][0]=i;
    fp(j,1,Log[n])fp(i,1,n-Mi[j-1]+1)
        f[i][j]=cmp(f[i][j-1],f[i+Mi[j-1]][j-1]);
    fp(i,1,n){
        while(Top&&a[S[Top]]>a[i])suf[S[Top--]]=i;
        pre[i]=S[Top];S[++Top]=i;
    }while(Top)pre[S[Top]]=S[Top-1],suf[S[Top--]]=n+1;
    fp(i,1,n)fr[i]=(ll)a[i]*(i-pre[i])+fr[pre[i]];
    fd(i,n,1)fl[i]=(ll)a[i]*(suf[i]-i)+fl[suf[i]];
    int x,y,L,R;
    fp(i,1,m)sd(x),sd(y),q[i]={x,y,x/Sz,i};
    sort(q+1,q+m+1);L=q[1].l,R=L-1;
    fp(i,1,m){
        x=q[i].l,y=q[i].r;
        while(L>x)Now+=left(L,R),L--;
        while(R<y)Now+=right(L,R),R++;
        while(L<x)Now-=left(L+1,R),++L;
        while(R>y)Now-=right(L,R-1),--R;
        ans[q[i].id]=Now;
    }
    fp(i,1,m)we(ans[i]);
return Ot(),0;
}

Algorithm2 猫树分治：

根据猫树的思想，我们考虑分开来计算代价。其中，\([l,m)\) 和 \([m,r]\) 的答案可以用单调栈线性预处理，就只需要考虑跨越部分了。对 \([l,m)\) 中记录每个数到 \(m\) 的区间最小值，考虑这个最小值贡献答案的区间的右端点 \(r\)，这个最右的右端点可以通过左右的归并得出。这样预处理之后，就能做到 \(\mathcal O(1)\)。的询问复杂度。这里的细节比较繁琐，不过多说明。

猫树，对于某个节点，先预处理出一个点到中点的答案。这可以使用单调栈求出。那么我们需要计算跨中点的贡献。

预处理出每个点到中点的最小值，并处理出这个最小值能延伸到右边哪里。这可以对左右两个区间进行一次归并得到。

贡献分为两种：最小值在左边的，我们在左端点处计算贡献；最小值在右边的，我们在右端点处计算贡献。

若查询左端点到中点的最小值不能延伸到右端点，则左边所有点都有到其延伸的右端点的完整的贡献。对于右半部分，左端点延伸的最远点左边的所有点都有完整的贡献，而右边到右端点的所有点都只有到左端点的贡献。这些东西都是可以拆开然后预处理出来的。

另一种情况的话同理可得。

代码实现上，这个到中点的前缀和很烦人，所以我分别保存的左边的答案和右边的答案。

另外这个做法其实是和那个 rmq 的做法本质相同，那个做法基本上相当于把这个做法搬到笛卡尔树上，然后就少了一堆特判……

时间复杂度：\(\mathcal O(n\log n)\)。

#include<cctype>
#include<cstdio>
using namespace std;
inline int readint(){
	int x=0;
	bool f=0;
	char c=getchar();
	while(!isdigit(c)&&c!='-') c=getchar();
	if(c=='-'){
		f=1;
		c=getchar();
	}
	while(isdigit(c)){
		x=x*10+c-'0';
		c=getchar();
	}
	return f?-x:x;
}
const int maxn=1e5+5;
int n,q,a[maxn*2];
typedef long long ll;
int pos[maxn*2];
ll s1[25][maxn*2],s2l[25][maxn*2],s2r[25][maxn*2];
int mn[25][maxn*2],pp[25][maxn*2];
ll s3l[25][maxn*2],s3r[25][maxn*2];
ll s4l[25][maxn*2],s4r[25][maxn*2];
int st[maxn],top;
void build(int o,int l,int r,int d){
	if(l==r){
		pos[r]=o;
		return;
	}
	int mid=l+(r-l)/2;
	build(o*2,l,mid,d+1);
	build(o*2+1,mid+1,r,d+1);
	ll res=0;
	st[top=0]=mid+1;
	for(int i=mid;i>=l;i--){
		while(top&&a[i]<a[st[top]]){
			res-=1ll*a[st[top]]*(st[top-1]-st[top]);
			top--;
		}
		st[++top]=i;
		res+=1ll*a[i]*(st[top-1]-i);
		s1[d][i]=i==mid?res:s1[d][i+1]+res;
		mn[d][i]=a[st[1]];
	}
	res=0;
	st[top=0]=mid;
	for(int i=mid+1;i<=r;i++){
		while(top&&a[i]<a[st[top]]){
			res-=1ll*a[st[top]]*(st[top]-st[top-1]);
			top--;
		}
		st[++top]=i;
		res+=1ll*a[i]*(i-st[top-1]);
		s1[d][i]=i==mid+1?res:s1[d][i-1]+res;
		mn[d][i]=a[st[1]];
	}
	int cur=r;
	for(int i=l;i<=mid;i++){
		while(cur>mid&&mn[d][cur]<mn[d][i]) pp[d][cur--]=i;
		pp[d][i]=cur;
	}
	for(int i=mid+1;i<=cur;i++) pp[d][i]=mid+1;
	for(int i=mid;i>=l;i--){
		s2l[d][i]=s2l[d][i+1]+1ll*mn[d][i]*(pp[d][i]-mid);
		s3l[d][i]=s3l[d][i+1]+1ll*mn[d][i]*mid;
		s4l[d][i]=s4l[d][i+1]+mn[d][i];
	}
	for(int i=mid+1;i<=r;i++){
		s2r[d][i]=s2r[d][i-1]+1ll*mn[d][i]*(mid+1-pp[d][i]);
		s3r[d][i]=s3r[d][i-1]+1ll*mn[d][i]*(mid+1);
		s4r[d][i]=s4r[d][i-1]+mn[d][i];
	}
}
int lg[maxn*4];
int main(){
	n=readint();
	q=readint();
	for(int i=1;i<=n;i++) a[i]=readint();
	int len=1;
	while(len<n) len*=2;
	build(1,1,len,1);
	for(int i=2;i<=n*4;i++) lg[i]=lg[i/2]+1;
	while(q--){
		int l,r;
		l=readint();
		r=readint();
		if(l==r){
			printf("%d\n",a[r]);
			continue;
		}
		int k=lg[pos[r]]-lg[pos[l]^pos[r]];
		ll ans=s1[k][l]+s1[k][r];
		if(pp[k][l]<r){
			ans+=s2l[k][l]+s2r[k][pp[k][l]];
			ans+=s3r[k][r]-s3r[k][pp[k][l]];
			ans-=(s4r[k][r]-s4r[k][pp[k][l]])*l;
		}
		else{
			ans+=s2r[k][r]+s2l[k][pp[k][r]];
			ans-=s3l[k][l]-s3l[k][pp[k][r]];
			ans+=(s4l[k][l]-s4l[k][pp[k][r]])*r;
		}
		printf("%lld\n",ans);
	}
	return 0;
}

P6406 [COCI 2014/2015 #2] Norma

没有修改&询问所有子区间的答案。

考虑猫树分治，假设当前指针 \(i\)，\(i\) 从 \(mid\) 到 \(l\) 倒序枚举，\([i,mid]\) 的最小值为 \(mn\)，最大值为 \(mx\)。

维护两个指针 \(p,q\) 表示 \([mid+1,r]\) 中第一个小于和第一个大于 \(mn,mx\) 的位置。那么对于 \(j \in [mid+1,r]\) 的 \(ans[i,j]\) 的贡献就可以分三类讨论。不妨设 \(p<q\)。

• \(j\in[mid+1,p-1]\) 时，区间最值不变，都是 \(mn,mx\)，直接求和即可。

  即：\(ans \leftarrow mn \times mx \times \sum_{j=mid+1}^{p-1} j-i+1\)

• \(j\in [p,q-1]\)，区间最大值不变，最小值就是 \([mid+1,j]\) 里面的最小值了。预处理 \([mid+1,r]\) 的最小值为 \(min_j\)，同时记录 \(min_j\) 和 \(min_j \times j\) 的前缀和即可。

  \(ans \leftarrow mx\sum_{j=p}^{q-1}min_j(j-i+1)\)

  \(ans \leftarrow mx\sum_{j=p}^{q-1}min_j\times j+mx(1-i)\sum_{j=p}^{q-1}min_j\)

• \(j\in[q,r]\)，最值和 \(mn,mx\) 无关，记录 \(min_j\times max_j\) 和 \(min_j\times max_j \times j\) 的前缀和即可。

  \(ans \leftarrow \sum_{j=q}^r min_j\times max_j(j-i+1)\)

  \(ans \leftarrow \sum_{j=q}^{q}min_j\times max_j\times j+(1-i)\sum_{j=q}^r min_j\times max_j\)

时间复杂度：\(\mathcal O(n\log n)\)。

#include<bits/stdc++.h>
#define int long long
#define LL long long
#define G if(++ip==ie)fread(ip=buf,1,N,stdin)
#define A(V) (ans+=V)%=YL
using namespace std;
const LL N=5e5+50,YL=1e9;

LL ans,a[N],mns[N],mxs[N],mnj[N],mxj[N],mms[N],mmj[N];
inline LL S(int l,int r){//高斯求和
    return (l+r)*(r-l+1)/2%YL;
}
void solve(int l,int r){
    if(l==r){A(a[l]*a[l]%YL);return;}
    int m=(l+r)>>1,i,j,p,q,mn=YL,mx=0;
    solve(l,m);solve(m+1,r);
    mns[m]=mxs[m]=mnj[m]=mxj[m]=mms[m]=mmj[m]=0;
    for(j=m+1;j<=r;++j){//预处理，变量名不解释
        mn=min(mn,a[j]);mx=max(mx,a[j]);
        mns[j]=(mns[j-1]+mn)%YL;
        mxs[j]=(mxs[j-1]+mx)%YL;
        mnj[j]=(mnj[j-1]+mn*j)%YL;
        mxj[j]=(mxj[j-1]+mx*j)%YL;
        mms[j]=(mms[j-1]+mn*mx)%YL;
        mmj[j]=(mmj[j-1]+mn*mx%YL*j%YL)%YL;
    }
    mn=YL;mx=0;
    for(p=q=m+1,i=m;i>=l;--i){//计算答案
        mn=min(mn,a[i]);mx=max(mx,a[i]);
        while(p<=r&&mn<a[p])++p;//单调移动
        while(q<=r&&mx>a[q])++q;
        if(p<q){
            A(mn*mx%YL*S(m-i+2,p-i));//注意做减法的都要加一下模数
            A(((mnj[q-1]-mnj[p-1])%YL+YL)%YL*mx%YL+((mns[q-1]-mns[p-1])%YL+YL)%YL*(1-i+YL)%YL*mx%YL);
            A((((mmj[r]-mmj[q-1])%YL+YL)%YL+(mms[r]-mms[q-1]+YL)*(1-i+YL)%YL)%YL);
        }
        else{
            A(mn*mx%YL*S(m-i+2,q-i)%YL);
            A((((mxj[p-1]-mxj[q-1])%YL+YL)%YL*mn%YL+((mxs[p-1]-mxs[q-1])%YL+YL)%YL*mn%YL*(1-i+YL)%YL)%YL);
            A((((mmj[r]-mmj[p-1])%YL+YL)%YL+(mms[r]-mms[p-1]+YL)%YL*(1-i+YL)%YL));
        }
    }
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
    int n;cin>>n;
    for(int i=1;i<=n;++i)cin>>a[i],a[i]%=YL;
    solve(1,n);
    cout<<(ans%YL+YL)%YL<<endl;
    return 0;
}

7023 -- 【NOIP模拟】Tree Connectivity

要计算全局所有子区间，考虑猫树分治。

设当前分治中心为 \(mid\)，那么计算包含 \(mid\) 的区间 \([l,r]\) 有多少个，那么就必须满足以下条件：

• \([l,mid]\) 和 \([mid+1,r]\) 中的点到 \(mid\) 的路径经过的最小值为 \(l\)，最大值为 \(r\)。

列出了条件直接双指针求解即可。

时间复杂度：\(\mathcal O(n \log n)\)。

操作序列分治/线段树分治

概述

线段树分治其实个人更愿意认为它更像一种技巧而不是一个算法，即带撤销操作的时间分治。操作形式多为维护一些信息，操作可能有询问/执行操作/撤回操作，其操作的执行较为容易，但撤回困难。所以把操作，询问一起离线下来，每个操作只在时间轴上的一个区间生效，那么就可以在线段树上的这个区间打上操作的标记，维护信息，在叶子结点计算答案。

【洛谷日报#209】线段树分治总结 - 知乎

线段树分治学习笔记 - Xttttr - 博客园

线段树分治学习笔记 - 摸鱼酱 - 博客园

例题

P5214 [SHOI2014] 神奇化合物

动态加/删边，求连通块个数，可以离线。

因为可以离线就不用 LCT 了，直接操作序列分治树+回滚并查集维护每条边的生效区间和连通性即可。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

P7457 [CERC2018] The Bridge on the River Kawaii

动态加/删边修改边权MST，但是可以离线且 \(v\le 10\)。

拿到的第一感觉是 LCT，因为又加边又删边的，但是最多只能按照时间轴维护 \(x\) 和 \(y\) 是否连通，很难维护 \(x\) 到 \(y\) 路径上的最大边权。

但是我们注意到 \(v\le 10\)，我们可以按照边权扫描线，这样我们只需判断 \(x\) 和 \(y\) 是否连通即可。由于本题可以离线，我们使用线段树分治维护每条边的生效区间，再用回滚并查集维护连通性即可。时间复杂度：\(\mathcal O(v\times n \log^2 n)\)。

但是还有一种做法（我口胡的），我们同样按照边权扫描线，把边权 \(\le i\) 的边全部按照时间轴排序，现在转化为了判断 \(x\) 和 \(y\) 是否连通，用 LCT 即可。时间复杂度：\(\mathcal O(v\times n \log n)\)。

P3206 [HNOI2010] 城市建设

动态修改边权MST，但是可以离线。

我们考虑操作序列分治，对于一些边的生效区间在 \([l,r]\) 的边，我们不能直接加入并查集，因为可能它不在最后的最小生成树中，只能一直把边往下传，只有 \(l=r\) 时在暴力处理这些询问，但是这样边集有可能是 \(\mathcal O(m)\)，接受不了。

我们考虑如何缩小边集规模，因为当当前分治区间为 \([l,r]\) 时，我们称生效区间在 \([l,r]\) 的边为动态边，不在的称为静态边。注意称生效区间在 \([l,r]\) 表示的是，一条边的加入时间在 \([l,r]\) 中，或者删除时间在 \([l,r]\) 中，也就是说生效区间完全包含 \([l,r]\) 的边就是静态边，没有完全包含的就是动态边。

我们对动态边的处理是直接下传（因为我们无法确定它对最后的最小生成树的最终影响），但是对于静态边我们可以将一部分有用的边下传，没有用的就扔掉。

具体地，如果我们强制令生效区间在 \([l,r]\) 的边的边权为 \(-inf\)，再将动态边和静态边一起跑一遍最小生成树，如果最后静态边还在最小生成树里，那么就直接加入这条静态边，用并查集加入静态边后图的连通性。类似地，我们再强制令生效区间在 \([l,r]\) 的边的边权为 \(inf\)，再将动态边和静态边一起跑一遍最小生成树，如果最后静态边没有在最小生成树里，那么它肯定没有用，直接删除即可。

这样做后时间复杂度就是 \(\mathcal O(n \log^2 n)\) 的，即这样的剪枝优化效果很大。考虑证明：

第一个操作保证了最多只有 \(r-l\) 个点没被压缩，即最多会有 \(r-l\) 条动态边被下传，由于这些动态边的生效区间小于 \([l,r]\)，有可能传下去会到一个时间点 \(t\in[l,r]\) 中失效，也有可能静态边中有边比动态边更优，所以我们需要尽可能的找到这些边的平替静态边，因此平替静态边的数量最多也就是和动态边个数持平，为 \(\mathcal O(r-l)\)。找到平替边的过程我们可以直接把生效区间在 \([l,r]\) 的边暂时删除，这样排掉它们再做一次最小生成树，就可以找到平替边了，也就是第二个操作所干的事情。

对于第一个把边权赋值为 \(-inf\) 的操作，保证了最后没有被压缩的点最多为 \(r-l\) 个，那么证明往下传的边数最多为 \(r-l\) 条，第二个操作正是将边数变为 \(r-l\) 的步骤。

根据主定理，其时间复杂度就是标准的 \(\mathcal O(n \log n)\)，然后套上一个回滚并查集的 \(\log n\)，总时间复杂度为 \(\mathcal O(n \log^2 n)\)。

以后这种神仙题还是要多多见识，碰到了完全想不出来还可以这么剪枝优化。

P4585 [FJOI2015] 火星商店问题

注意到每个商品包括特殊商品都有自己的生效区间，且本题可以离线。那么我们考虑用线段树分治，一个商品的生效区间为 \([t,t+d]\)，把操作序列按照分治形式进行递归，把每个询问拆为 \(\log n\) 个区间，每次加入一个操作时就在可持久化01-trie上直接插入，最后询问编号 \([x,y]\) 之间的异或极值时就直接差分回答即可。

时间复杂度：\(\mathcal O(m \log m \log V)\)。

这是一道经典的线段树分治的题。一是计算操作影响的方式，这题需要 \(Trie\) 树。另一方面，这题变成了询问时间区间，操作是单点的。同样的思路，对于询问，我们把它询问的时间区间插入到线段树上，操作也插入到线段树上，同样的递归处理，由于每个询问依旧会得到操作的影响，所以复杂度和正确性依旧可以保证。具体实现的话，每次递归到一个结点，对于 \(n\) 个商店建一棵可持久化 \(Trie\) 树，这就能处理 \([L,R]\) 的问题了。

本题实际上是一道正难则反的题目，因为一般线段树分治是把询问挂在叶子节点，也就是询问是单点，但操作的时间是一个区间。但是本题不一样，操作是一个单点，询问是一个区间，那么我们就把操作挂在叶子节点，询问就像以前操作一样分成 \(\log n\) 个区间，这样同样可以操作来影响询问，效果是一样的。

#include<bits/stdc++.h>
#define maxn 100005
#define mid ((l+r)>>1)
#define rc ((rt<<1)|1)
#define lc (rt<<1)
using namespace std;
int gi()
{
    char c;int x,sign=1;
    while((c=getchar())>'9'||c<'0')if(c=='-')sign=-1;
    x=c-'0';while((c=getchar())>='0'&&c<='9')x=(x<<1)+(x<<3)+c-'0';
    return x*sign;
}
int n,m,cnt1,cnt2,tot,top;
int rt[maxn],ans[maxn],st[maxn];
int ch[maxn*20][2],sz[maxn*20];
vector<int> a[maxn];
struct guest{int l,r,L,R,x;}p[maxn];
struct buy{int s,v,t;}q[maxn],t1[maxn],t2[maxn];
bool cmp(const buy x,const buy y){return x.s<y.s;}
void insert(int &x,int u,int w)
{
    int now;now=x=++tot;
    for(int i=17;i>=0;i--)
    {
        bool d=w&(1<<i);
        ch[now][d^1]=ch[u][d^1];ch[now][d]=++tot;
        now=ch[now][d];u=ch[u][d];
        sz[now]=sz[u]+1;
    }
}
int query(int l,int r,int w)
{
    int res=0;
    for(int i=17;i>=0;i--)
    {
        bool d=w&(1<<i);
        if(sz[ch[r][d^1]]-sz[ch[l][d^1]]>0)
            l=ch[l][d^1],r=ch[r][d^1],res+=(1<<i);
        else l=ch[l][d],r=ch[r][d];
    }
    return res;
}
void update(int rt,int l,int r,int L,int R,int x)
{
    if(L>R||r<L||l>R)return ;
    if(L<=l&&r<=R){a[rt].push_back(x);return;}
    update(lc,l,mid,L,R,x);update(rc,mid+1,r,L,R,x);
}
void calc(int x,int L,int R)
{
    top=tot=0;
    for(int i=L;i<=R;i++)
    {
        st[++top]=q[i].s;
        insert(rt[top],rt[top-1],q[i].v);
    }
    for(int i=0,sz=a[x].size();i<sz;i++)
    {
        int k=a[x][i],t;
        int l=upper_bound(st+1,st+1+top,p[k].l-1)-st-1;
        int r=upper_bound(st+1,st+1+top,p[k].r)-st-1;
        ans[k]=max(ans[k],t=query(rt[l],rt[r],p[k].x));
        //cout<<x<<" "<<k<<" "<<t<<endl;
    }
}
void divide(int rt,int l,int r,int L,int R)//按时间分治
{
    if(L>R)return;
    int cn1=0,cn2=0;
    calc(rt,L,R);
    if(l==r)return;
    for(int i=L;i<=R;i++)//修改的区间右端点都是cnt1,相当于影响到之后的时间
        if(q[i].t<=mid)t1[++cn1]=q[i];
        else t2[++cn2]=q[i];
    for(int i=1;i<=cn1;i++)q[i+L-1]=t1[i];//左端点在mid左边的放在左区间
    for(int i=1;i<=cn2;i++)q[i+L-1+cn1]=t2[i];//否则放右边
    divide(lc,l,mid,L,L+cn1-1);
    divide(rc,mid+1,r,L+cn1,R);
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)insert(rt[i],rt[i-1],gi());
    for(int i=1,ty,l,r,x,d,s,v;i<=m;i++)
    {
        ty=gi();
        if(!ty)s=gi(),v=gi(),q[++cnt1]=(buy){s,v,cnt1};//起点,价格,时间
        else
        {
            l=gi(),r=gi(),x=gi(),d=gi();
            ans[++cnt2]=query(rt[l-1],rt[r],x);
            p[cnt2]=(guest){l,r,max(1,cnt1-d+1),cnt1,x};
            //商店左端点,商店右端点,开始时间,结束时间,喜好密码
        }
    }
    for(int i=1;i<=cnt2;i++)update(1,1,cnt1,p[i].L,p[i].R,i);
    sort(q+1,q+1+cnt1,cmp);//按照商店编号排序
    divide(1,1,cnt1,1,cnt1);
    for(int i=1;i<=cnt2;i++)printf("%d\n",ans[i]);
    return 0;
}

CDQ分治

例题

SP2371 LIS2 - Another Longest Increasing Subsequence Problem

二维 LIS，相当于值域二维偏序，下标一维偏序。

CDQ 分治即可。详细见DP部分的整体DP。

P3769 [CH弱省胡策R2] TATT

这题是板的四维偏序。这里讲述CDQ套CDQ的做法。

先说一下弱化版，所有点不重复。

step 1： 对第一维进行排序。

step 2：对第1维重新标号（left或right），然后对第2维分治，递归解决子问题，按照第2维的顺序合并。此时只是单纯的合并，并不进行统计。

step 3： 把合并后的序列复制一份，在复制的那一份中进行cdq分治。（这时第2维默认有序）即对第3维分治，递归解决子问题，按照第3维的顺序合并。合并过程中用树状数组维护第4维的信息。

根据整体DP的思想，我们CDQ分治时需要先遍历 \([l,mid]\) 再遍历 \([mid+1,r]\) 即可。

P4849 寻找宝藏

类似题目，只不过要求方案数，所以可以直接计算。

SP30759 ADACABAA - Ada and Species

三倍经验。

CF1045G AI robots

启示：关于偏序关系的问题时，我们往往先处理限制性最强的一个条件。

譬如本题，我们要静态求解合法点对 \(i,j\) 的数量，其中 \(i,j\) 表示一个三元组：\(x_i,r_i,q_i\)。合法条件为：\(|x_i-x_j| \le \min(r_i,r_j),|q_i-q_j|\le K\)。其中 \(K\) 为常量。

观察上述条件，如果我们以 \(x\) 或者 \(q\) 来排序的话，我们对这个 \(\min(r_i,r_j)\) 的条件限制很难处理。

于是我们考虑直接按照 \(r\) 来进行从大到小排序，这样我们就只需在 \(i\) 处时统计有多少 \(j\)，满足 \(j < i\) 且 \(|x_i-x_j|\le r_i,|q_i-q_j| \le K\)。

拆开式子，我们要统计合法的 \(j\) 满足 \(j<i,x_i-r_i\le x_j\le r_i+x_i,q_i-K\le q_j \le q_i+K\)。

如果我们现在进行 CDQ 分治时，我们还需要用一个数据结构动态维护后面那一坨东西，很明显直接暴力维护只能用树套树，那么时间复杂度为 \(\mathcal O(n \log^3 n)\)，很劣。

但是注意到合法点对个数可以容斥，即合法点对个数=总点对个数-不合法点对个数。那么我们就可以不用树套树维护二维动态偏序，而是直接用值域树状数组维护动态一维偏序即可。

所以时间复杂度为：\(\mathcal O(n \log^2 n)\)。

根号分治/平衡规划

概述

\(\textcolor{red}{定义(平衡规划)}\)，针对不同的数据规模提出不同的算法，使得算法之间的复杂度较为均衡。

根号分治：

根号分治核心思想在于将信息按照某种特征划分为两类分别处理。

• 种类少但出现次数多：使用数据结构存储各种类信息。
• 种类多但出现次数少：枚举所有出现元素。

使用根号分治的要求是题目中数据结构存在反比例特征。

• 和固定时，数字大小&出现次数
• 剩余类的约数个数&倍数个数
• 二进制高位&低位

集合和平衡

若 \(\textcolor{red}{集合中元素和固定}\)，则数字大小与数字出现次数成反比。

此时，即可通过 \(\textcolor{red}{种类数和出现次数的优势对于小数和大数分别设计算法}\)。

算法：（集合和平衡）

• 集合元素和 \(S\) 固定时，数字大小与数字出现次数成反比
• 设根号分治阈值为 \(B\)
• 若数字大小 \(x\le B\)
  • \(x\) 的种类数不超过 \(B\)
  • 对于 \(\mathcal O(B)\) 种数字使用数据结构预处理信息。
• 若数字大小 \(x>B\)
  • 所有 \(x>B\) 的数字总出现个数 \(\sum_{x>B} cnt_x<\mathcal O(\frac{S}{B})\)
  • 枚举所有 \(\mathcal O(\frac{n}{B})\) 个元素分别处理信息即可。

时间复杂度

设数据结构的操作复杂度为 \(f(x)\)，单个元素的处理时间为 \(g(x)\)，总时间复杂度为 \(\mathcal O(B\times f(x)+\frac{S}{B} \times g(x))\)。

\(\textcolor{red}{数字和种类数}\)：集合 \(a\) 中元素和为 \(S\)，则集合数字种类数不超过 \(\mathcal O(\sqrt{S})\)。

对于图论中度数相关的做法，会受到菊花图等特殊图的影响导致时间复杂度退化。

若图中边数量固定，则度数与点数量成反比。

此时即可通过点度数和个数的优势，对于大度点和小度点分别设计算法。

例题

AT_joisc2018_h ビ太郎のパーティー (Bitaro's Party)

注意到 \(\sum_{i=1}^q Y_i\le 10^5\)。所以考虑虚树的思想，询问只限制的这么些点，所以直接考虑集合和平衡。

设阈值为 \(B\)，设询问限制的点的个数为 \(x\)，那么开始分类讨论。

• 当 \(x<B\) 时，那么询问只有这么点限制，我们可以预处理出答案，询问时直接回答。具体地，我们先用拓扑排序边拓扑边记录离这个点距离的前 \(k\) 大的点。这个可以用堆+拓扑排序来做。时间复杂度 \(\mathcal O(n\times B\times \log n)\)。
• 当 \(x\ge B\) 时，直接暴力处理这些询问即可，即用拓扑排序来做，时间复杂度：\(\mathcal O(\frac{n}{B}\times (n+m))\)。

当 \(B=\sqrt{\frac{n}{\log n}}\) 时时间复杂度最优，为 \(\mathcal O(n\times \sqrt{\frac{n}{\log n}} \times \log n)\)。

CF348C Subset Sums

注意到 \(\sum_{i=1}^n |S_i|\le n\)，考虑集合和平衡。设阈值为 \(B\)，我们称大小小于 \(B\) 为轻集合，大小大于 \(B\) 的为重集合。设 \(C_{i,j}\) 表示 \(i\) 这个重集合与 \(j\) 这个轻集合的交的个数。

那么我们对于这些集合分类讨论：

• 当前集合为轻集合，则修改时间复杂度为 \(\mathcal O(B)\)。具体地，先用 \(\mathcal O(B)\) 的时间修改自身集合，再用 \(\mathcal O(\frac{n}{B})\) 的时间修改与重集合的交的部分，即用 \(sum_j\leftarrow \Delta_i\)。
• 轻集合询问时间复杂度为先用 \(\mathcal O(B)\) 的时间复杂度询问自身集合的和，再加上重集合与轻集合的贡献，由于重集合只有 \(\mathcal O(\frac{n}{B})\) 个，所以直接用 \(\mathcal O(\frac{n}{B})\) 的时间加上重集合的贡献，即每个重集合 \(i\) 加上的值 \(\operatorname{tag}_i\)，贡献为 \(\operatorname{tag}_i\times C_{i,j}\)。
• 重集合的修改复杂度为 \(\mathcal O(1)\)，即 \(\mathcal O(1)\) 的时间修改 \(\operatorname{tag}_x\)，再用 \(\mathcal O(1)\) 的时间修改 \(sum_x\)。
• 重集合的询问时间复杂度为 \(\mathcal O(B)\)，答案即为 \(sum_x+C_{i,j} \times \operatorname{tag}_x\)。

总之就是说重集合对重集合的贡献（更新 \(\operatorname{tag}_x\)），重集合对轻集合的贡献（更新 \(\operatorname{tag}_x\)），轻集合对重集合的贡献（枚举重集合加上轻集合的贡献），轻集合对轻集合的贡献（暴力修改）。

查询重集合就是 \(sum_x\) 加上轻集合对它的贡献，查询轻集合就是暴力枚举轻集合的贡献再加上重集合对它的贡献 \(\operatorname{tag}_i \times C_{j,i}\)。

时间复杂度：当 \(\mathcal O(B)=\sqrt{n}\) 时时间复杂度最优，为 \(\mathcal O(n\sqrt{n})\)。

CF1446D1 Frequency Problem (Easy Version)

如果原序列里，出现次数最多的数不唯一，则答案就是 \(n\)。否则，考虑那个唯一的、出现次数最多的元素，记为 \(x\)。

类似 \(mex\) 的性质，我们同样可以证明在最终的最长的、好的子段（也就是答案）中 \(x\) 必定是其中出现次数最多的元素之一。

证明：考虑反证法。

假设在最终的子段中 \([l,r]\) 出现次数最多的不包含 \(x\)，那么一定能找到一个区间 \([l',r'],l'\le l,r'\ge r,r'-l'>r-l\)，使得 \(x\) 出现次数最多，且有多个出现次数最多的数，所以与假设矛盾。

我们枚举，答案的子段里，和 \(x\) 出现次数一样多的元素是谁，记为 \(y\)。问题转化为，对一组数值 \((x,y)\) 计算答案。

我们可以忽略数列里除 \(x, y\) 外的其他数。问题进一步转化为：求一个最长的子段，满足 \(x, y\) 的出现次数一样多。

把数列里的 \(x\) 看做 \(1\)，\(y\) 看做 \(−1\)，其他数看做 \(0\)。得到一个序列 \(b\)。那么，我们要求最长的、和为 \(0\) 的子段长度。我们又注意到此题最多只有 \(100\) 种不同的数值，所以我们暴力枚举 \(y\)，记 \(b_{y,i}\) 表示如果 \(a_i=x\)，则 \(b_{y,i}=1\)，如果 \(a_i=y\)，则 \(b_{y,i}=-1\)，其余情况为 \(0\)。那么再设 \(sum_{y,i}=\sum_{j=1}^i b_{y,j}\)，问题转化为找两个位置 \(0\le l <r \le n\)，满足 \(sum_{y,l-1}=sum_{y,r}\)。

时间复杂度：\(\mathcal O(n \times maxa)\)。

注意：D1没有运用到集合和平衡。

CF1446D2 Frequency Problem (Hard Version)

记数 \(i\) 的出现次数为 \(g_i\)，那么显然 \(\sum_{i=1}^n g_i=n\)，也就是出现次数集合和平衡。

那么我们可以使用根号分治。考虑答案里出现次数最多的数 \(x\)。

1. 如果其在答案中出现次数不超过 \(\sqrt{n}\)，则满足条件的数值只有不超过 \(\sqrt{n}\) 个，我们套用 D1 的做法，时间复杂度 \(\mathcal O(n\sqrt{n})\)。

2. 如果出现最多的数，出现次数 \(\sqrt{n}\)，我们枚举这个出现次数，记为 \(t\)。然后做 two pointers。

   具体来说，枚举答案区间的右端点 \(r\)。对每个 \(r\)，记最小的，使得 \([l,r]\) 内所有数出现次数都 \(\le t\) 的最小的 \(l\) 为 \(L_r\)。容易发现，对于 \(r=1,2,…,n\)，\(L_r\) 单调不降。并且，在当前的 \(t\) 下，对一个 \(r\) 来说，如果 \([L_r,r]\) 不是好的子段（即出现次数为 \(t\) 的数值，不到 \(2\) 个），那么其他 \([l,r](L_r<l≤r)\) 也不可能是。因为出现次数为 \(t\) 的数值，只会更少。

   所以，随着我们从小到大枚举 \(r\)，只需要用一个变量来记录当前的 \(L_r\)。同时用数组维护一下，当前每个数的出现次数，以及每个出现次数的出现次数。就能确定，当前的 \([L_r,r]\) 是否是好的区间。这个 two pointers 的过程是 \(\mathcal O(n)\) 的。因为有 \(n\) 个 \(t\)，所以这部分的时间复杂度也是 \(\mathcal O(n\sqrt{n})\)。

P5901 [IOI 2009] Regions

考虑根号分治，称大小大于 \(n\) 的集合为大集合，其它集合为小集合。

当 \(r_1\) 为大集合时，考虑预处理所有这样的询问的答案。对每个大集合 \(r_1\)，集合 \(r_2\) 的答案为 \(\sum_{i\in r_2}c_i\)，其中 \(c_i\) 表示集合 \(r_1\) 中 \(i\) 的祖先的数量，时间复杂度 \(\mathcal O(n)\)。因为有不超过 \(n\) 个大集合，所以总复杂度 \(\mathcal O(n\sqrt{n})\)。

当 \(r_2\) 为大集合时，同样的，预处理所有这样的询问的答案，只需要将 \(c_i\) 的定义改为集合 \(r_2\) 中 \(i\) 的子节点的数量。

当 \(r_1,r_2\) 均为小集合时，总共只会涉及到 \(\mathcal O(\sqrt{n})\) 个点。\(r_1\) 的每个点对应一个时间戳区间，\(r_2\) 的每个点对应一个时间戳，每个时间戳落在每个时间戳区间都会产生 \(1\) 的贡献。相当于先进行若干次区间加 \(1\)，再进行若干次单点查询。 对坐标区间扫描线，遇到左端点就将当前区间数 \(+1\)，遇到右端点就将当前区间数 \(−1\)。预处理排序即可做到单次 \(\mathcal O(\sqrt{n})\)。

总时间复杂度 \(\mathcal O((n+q)\sqrt{n})\)，空间复杂度 \(\mathcal O(n+R\sqrt{n})\)。

这道题的启发在于：思考不同数据范围的特性，并用不同的适应于这个数据范围的算法解决。

51nod-1597 有限背包计数问题

多重背包方案数问题，使用通用算法最坏为 \(\mathcal O(n^2)\)。

背包问题=集合大小之和不超过容量，因此可以考虑集合和平衡。

设阈值为 \(B\)。

• 若物品大小 \(i \ge B\)

  物品至多使用 \(\frac{n}{i}<i\)，转化为完全背包。

  转化为通过 \([B,n]\) 的物品任意选择组合为容量为 \(n\) 的所有方案。

  直接使用完全背包求解，可选的种类数 \(\mathcal O(n-B)\) 种，总复杂度仍为 \(\mathcal O(n^2)\)。

  \(i>B\) 的物品实际使用个数不超过 \(\mathcal O(\frac{n}{B})\)，考虑只枚举实际使用的种类数。

  问题转化求解为 \([B,n]\) 中选择 \(\mathcal O(\frac{n}{B})\) 个数字，使得容量为 \(n\) 的方案数。

  设 \(f_{i,j}\) 表示 \(i\) 个数字之和为 \(j\) 的方案数——分拆数。

  为了避免算重，考虑强行定序，保证选出的数字序列非降。

  

  考虑和固定的非降序列计数，转移时直接记录最后一个数字大小，无法保证时间复杂度。

  正难则反，每次转移让当前所有数字大小 \(+1\)，或者引入一个新数字即可。

  注意保证新数字 \(\ge B\)。

  设 \(g_{i,j}\) 表示选择了 \(i\) 个大小超过 \(\sqrt{n}\) 的物品，容量之和为 \(j\) 的方案数。考虑添加一个大小为 \(\sqrt{n}\) 的物品，或者将所有物品大小加一，有：

  \[g_{i,j}=g_{i,j-i}+g_{i-1,j-\sqrt{n}} \]

  时间：\(\mathcal O(\frac{n}{B}\times n)\)。

• 若物品大小 \(i < B\)

  物品种类数为 \(\mathcal O(B)\)，每个物品多重背包，\(f_{i,j}\) 表示前 \(i\) 个物品容量为 \(j\) 的方案数。

  转移为：\(f_{i,j}=\sum_{k=0}^i g_{i-1,j-k\times i}\)。

  时间：\(\mathcal O(B \times n)\)。

\(f\) 和 \(g\) 乘法原理组合为容量 \(n\) 即可。

CF1039D You Are Given a Tree

首先考虑如果 \(k\) 是定值，能不能快速求出答案。一眼感觉挺像树形 DP，实际上不完全是。

假设现在位于 \(p\) 点，则路径的选取有两种可能：选一个儿子接到 \(p\) 上形成一条长度加 \(1\) 的链，继续往上接；选两个儿子和 \(p\) 接起来形成一条长度为两个儿子下面接的链的长度加上 \(1\) 的链，上面重新开一条新链。

如果是第一种情况的话显然取子树里那条最长的链往上连是最优的，更容易出现长度足够的路径。

考虑什么时候用第二种情况。设它的儿子所在的最长、次长链分别为 \(a,b\)。首先直接取 \(a,b\) 来配是最容易出现长度达到 \(k\) 的新路径的。

然后猜有这么个结论：如果 \(a,b\) 配起来长度达到 \(k\)，那么先把 \(a,b\) 放到一起配成新路径是肯定不会比单独取 \(a\) 往上连的结果要劣的。当然如果配不上就不得不选第一种情况了。

于是我们获得了一个 \(O(n^2)\) 的过不了做法。

发现 \(k\) 与答案的乘积不会超过 \(n\)，启动根号分治。

当 \(k\le \sqrt{n}\) 的时候，直接按上面方法贪心预处理求出每一个点在每一个 \(k\) 下的答案即可。

当 \(k>\sqrt{n}\) 的时候，答案不会超过 \(\sqrt{n}\)。考虑反过来枚举答案，求有哪些 \(k\) 是这个答案。意识到答案随 \(k\) 的增大而减小，于是答案相等的 \(k\) 一定在一段区间内，二分跑 \(\log n\) 次树形 DP 求出每个答案第一次被取到的 \(k\) 即可。

于是我们获得了一个 \(O(n\sqrt{n}\log n)\) 的理论能过做法。

然而实践发现被卡常了，所以有几个小优化：

• 可以把 dfs 序和每个点的祖先预处理出来再按顺序跑，除掉递归的常数。到这里 6s。
• 每次二分的时候并不需要对整个 \([1,n]\) 都找一遍。如果从小到大枚举答案的话，你已经确定了前面答案所在的区间，位于整个 \([1,N]\) 的尾部，那把二分右端点放在上一个答案的前一位跑就够了。到这里 3s。
• 注意到按 \(\sqrt{n}\) 分割的话两部分做法时间复杂度并不统一，理论上取 \(\sqrt{n\log n}\) 才是最优的。到这里 2s。

CF1790F Timofey and Black-White Tree

顶级诈骗题。

先放一个重要的结论：在将 \(x\) 个点染黑后，答案（即两两黑色点对的最小距离）为 \(\dfrac{n}{x}\) 级别（实际上界约为 \(\dfrac{2n}{x}\)）。

考虑一个很显然的暴力乱搞，令一个 \(dis\) 数组 \(dis_i\) 表示离节点 \(i\) 最近的一个黑色节点。每把一个点染黑，便从这个点开始做一遍搜索更新 \(dis\) 数组。若当前节点有更近的黑色节点，或当前节点离新加入的黑色节点的距离大于当前的答案，那么此时继续搜索没有意义，退出。

上述做法正确性显然，同时，这个看上去很假的东西复杂度是对的，为 \(\mathcal{O}(n\sqrt{n})\)，同时也是官方题解和 jiangly 的做法。

我们来分析一下复杂度：

首先在经过 \(\sqrt{n}\) 次操作后，答案不会超过 \(\dfrac{n}{\sqrt{n}}=\sqrt{n}\)，因此所有有意义的 \(dis_i\) 的值都不会超过 \(\sqrt{n}\)，在我们上述的操作过程中，\(dis_i\) 显然是单调不增的，因此在这之后，每个 \(dis_i\) 显然也只会被更新 \(\sqrt{n}\) 次，因此后面的操作总复杂度是 \(\mathcal{O}(n\sqrt{n})\) 的。而前 \(\sqrt{n}\) 操作中，即使每次操作都满打满算单次复杂度 \(\mathcal{O}(n)\)，那么 \(\sqrt{n}\) 次操作总复杂度也不过是 \(\mathcal{O}(n\sqrt{n})\) 的。

因此该算法的复杂度是 \(\mathcal{O}(n\sqrt{n})\) 的，可以通过本题，如果你超时了请尝试将搜索边界写的紧一点。

以上算法还能继续优化。

每次操作我们都进行一遍搜索的开销太大，我们考虑只进行向上更新，即对于每一个节点，我们一步步跳父亲并更新答案。

这个的正确性看上去不太显然，因为在加入节点时，其子树内的节点是否会被计算到？

答案是会，因为当其子树内部的点存在黑点时，在其向上更新的过程中，也会将这个点计算一遍答案，因此不会出现正确性上的问题。

至于复杂度，由于我们向上跳节点的次数不会超过当前答案（超过了一定不优），因此总复杂度为 \(\mathcal{O}(\sum_{i=1}^{n}ans_i)\)，其中 \(ans_i\) 为加入第 \(i\) 个节点时的答案，初始黑点视为第一个节点。而我们知道 \(ans_i\leq \dfrac{n}{i}\)，因此总复杂度为 \(\mathcal{O}(\sum_{i=1}^{n}\dfrac{n}{i})\)，这是一个经典的调和级数形式，因此复杂度为 \(\mathcal{O}(n\log n)\)，本做法也是 tourist 的做法。

还有很多做法，比如大冤种点分树做法，与 CF342E 类似，不多展开，也是我赛时被诈骗写的做法。

不过个人来看，本题不能完全算与上题重题，因为巧妙利用答案的上界解题思路是这题有而上题没有的。

\(\mathcal{O}(n\sqrt{n})\) 实现：

#include<bits/stdc++.h>
using namespace std;
int t,n,s,ans,nxt[400005],head[200005],go[400005],k,dis[200005],a[200005];
void add(int u,int v)
{
	nxt[++k]=head[u];
	head[u]=k;
	go[k]=v;
}
void bfs(int s)
{
	dis[s]=0;
	queue<int> q;
	q.emplace(s);	
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		if(dis[x]>=ans) break ;
		for(int i=head[x];i;i=nxt[i])
		{
			int g=go[i];
			if(dis[g]<=dis[x]+1) continue ;
			dis[g]=dis[x]+1;
			q.emplace(g);
		}
	}
}
int main()
{
	cin>>t;
	while(t--)
	{
		cin>>n>>s;
		fill(dis+1,dis+1+n,n+1);
		fill(head+1,head+1+n,0);
		k=0;
		ans=n+1;
		for(int i=1;i<n;i++)
		{
			cin>>a[i];
		}
		for(int i=1;i<n;i++)
		{
			int u,v;
			cin>>u>>v;
			add(u,v);
			add(v,u);
		}
		bfs(s);
		for(int i=1;i<n;i++)
		{
			ans=min(ans,dis[a[i]]);
			bfs(a[i]);
			cout<<ans<<" ";
		}
		cout<<"\n";
	}
}

\(\mathcal{O}(n\log n)\) 实现：

#include<bits/stdc++.h>
using namespace std;
int t,n,s,ans,nxt[400005],head[200005],go[400005],k,dis[200005],a[200005],f[200005];
void add(int u,int v)
{
	nxt[++k]=head[u];
	head[u]=k;
	go[k]=v;
}
void add(int x)
{
	int d=0,p=x;
	while(p&&d<ans)
	{
		ans=min(ans,dis[p]+d);
		dis[p]=min(dis[p],d);
		p=f[p];
		d++;
	}
}
void dfs(int x,int fa)
{
	f[x]=fa;
	for(int i=head[x];i;i=nxt[i])
	{
		int g=go[i];
		if(g!=fa) dfs(g,x);
	}
}
int main()
{
	cin>>t;
	while(t--)
	{
		cin>>n>>s;
		fill(dis+1,dis+1+n,n+1);
		fill(head+1,head+1+n,0);
		k=0;
		ans=n+1;
		for(int i=1;i<n;i++)
		{
			cin>>a[i];
		}
		for(int i=1;i<n;i++)
		{
			int u,v;
			cin>>u>>v;
			add(u,v);
			add(v,u);
		}
		dfs(1,0);
		add(s);
		for(int i=1;i<n;i++)
		{
			ans=min(ans,dis[a[i]]);
			add(a[i]);
			cout<<ans<<" ";
		}
		cout<<"\n";
	}
}

P1989 无向图三元环计数

我们考虑给所有的边一个方向。具体的，如果一条边两个端点的度数不一样，则由度数较小的点连向度数较大的点，否则由编号较小的点连向编号较大的点。不难发现这样的图是有向无环的。注意到原图中的三元环一定与对应有向图中所有形如 \(<u \rightarrow v>,<u \rightarrow w>,<v \rightarrow w>\) 的子图一一对应，我们只需要枚举 \(u\) 的出边，再枚举 \(v\) 的出边，然后检查 \(w\) 是不是 \(u\) 指向的点即可。

下面证明这个算法的时间复杂度是 \(O(m \sqrt m)\)。

首先我们可以在枚举 \(u\) 的出边时给其出点打上 \(u\) 的时间戳，这样在枚举 \(v\) 的出边时即可 \(O(1)\) 去判断 \(w\) 是不是 \(u\) 的出点。

那么考虑对于每一条边 \(<u \rightarrow v>\)，它对复杂度造成的贡献是 \(out_v\)，因此总复杂度即为 \(\sum_{i = 1}^m out_{v_i}\)，其中 \(v_i\) 是第 \(i\) 条边指向的点，\(out_v\) 是点 \(v\) 的出度。

考虑分情况讨论。

1. 当 \(v\) 在原图（无向图）上的度数不大于 \(\sqrt m\) 时，由于新图每个节点的出度不可能大于原图的度数，所以 \(out_v = O(\sqrt m)\)。
2. 当 \(v\) 在原图上的度数大于 \(\sqrt m\) 时，注意到它只能向原图中度数不小于它的点连边，又因为原图中所有的点的度数和为 \(O(m)\)，所以原图中度数大于 \(\sqrt m\) 的点只有 \(O(\sqrt m)\) 个。因此 \(v\) 的出边只有 \(O(\sqrt m)\) 条，也即 \(out_v = O(\sqrt m)\)。

因此所有节点的出度均为 \(O(\sqrt m)\)，总复杂度 \(\sum_{i = 1}^m out_{v_i} = O(m \sqrt m)\)。

6905 -- 【模板】四元环计数--地形计算

四元环计数。

这个比三元环计数稍微复杂些，但还不算困难。

考虑一个四元环 \((A,B,C,D)\) 对应到图上有哪些可能，列举一下也无非就以下三种：

• \(A→B,B→C,A→D,D→C\)
• \(A→B,B→C,C→D,A→D\)
• \(A→B,A→D,C→B,C→D\)

考虑对三种情况一一计数，对于第一种情况我们枚举 \(A\)，我们记以 \(C\) 结尾的满足存在边 \(A→B,B→C\) 的点 \(B\) 个数为 \(f_C\)，那么这样的四元环个数即为 \(∑_C\dbinom{f_c}{2}\)，这个在枚举 \(C\) 的过程中可以求得。

对于第二、三种情况，有一个注意点，就是对于一个点 \(A\) 而言，求满足存在 \(A←B,B→C\) 的点 \(B\) 个数 \(cnt_C\) 直接枚举是没问题的，但是求满足存在 \(A→B,B←C\) 的点 \(B\) 个数就不能直接枚举了，因为在新建的图中每个点的入度是没有任何性质的，一个菊花图就能把你卡成 \(n^2\)。

因此在第二种情况中考虑枚举 \(B\)，那么就可以将四元环拆成两个基本模型 \(B→C,C→D\) 和 \(B←A,A→D\)，这两部分都是可以 \(m\sqrt{m}\) 枚举的，记两部分个数分别为 \(f_D\) 和 \(g_D\)，那么这样的四元环个数就是 \(∑_Df_Dg_D\)。

对于第三种情况考虑枚举 BB，那么也可以拆成两个基本模型 \(B←C,C→D\) 和 \(B←A,A→D\)，这一类的贡献即为 \(∑_D\dbinom{g_D}{2}\)，但由于 \(B,D\) 地位相同，故同一个这一类的四元环会被算两次，需除以 \(2\)。

最终四元环个数即为这三种情况贡献之和。时间复杂度还是 \(\mathcal O(m\sqrt{m})\)。

核心思想：枚举了一条边后到另一个端点时只能枚举这个点的出边，不能枚举这个点的入边。

P6815 [PA 2009] Cakes

三元环计数板子题。

P8427 [COI 2020] Paint

先设 \(n=rs\)，然后考虑两个暴力。

• 暴力 1：每次暴力 \(\tt dfs\) 当前联通块的邻居，暴力合并。
• 暴力 2：vector 数组记录一个点的所有邻居，每种颜色的邻居，修改的时候找到对应颜色的邻居合并。然后更新上述数组。

常规手段，用根号摊平两个暴力：我们按联通块的大小分类，称大小 \(\le\sqrt n\) 的为小块，大的为大块。对于每块，记录由 vector 构成的数组如下

1. V 代表其所有大块的邻居（仅大块）
2. C[] 代表其每个颜色的邻居（仅大块）
3. P 代表其所有在块中的节点（所有块都要维护）

• 小块的修改：暴力找到其对应颜色邻居，然后合并。最后需要更新其邻居的 V，C[] 数组。
• 大块的修改：沿着 C[] 找到其对应颜色邻居，同样合并。最后需要更新其邻居的 V，C[] 数组。
• 两块的合并：启发式，让小的合并向大的，这样可以保证每次只合并 \(\log\) 次。合并的过程就是把一方的三个数组全部塞到另一方。
• 小块变大块：直接暴力搜索，记录下其三个数组。

大块个数最多只有 \(\frac{n}{B}\) ，所以这里空间复杂度上界为 \(O(\frac{n^2}{B})\)（实际常数很小）。

再考虑两个块的合并，我们采用启发式合并，每次将小的集合连向大的集合。

由于每个连通块的合并次数不会超过 \(\log\) 次，每次小块寻找邻居的复杂度最多为 \(B\) 级别的，大块寻找邻居是 \(O(\frac{R\times S}{B})\) 级别的， 所以复杂度大约是 \(O(R\times S\times \log(R\times S)+Q\times B+\frac{Q\times R\times S}{B})\)。即 \(O(n\sqrt n)\) 级别的。

实现细节：

• 关于三个数组：V,P 开成 vector<int>[N] 的形式，C[] 开成 unordered_map<int,vector<int>>[N] 的形式。
• 关于联通块之间的被包含关系：可以开成并查集的形式，路径压缩/启发式合并一起使用可以让这部分时间几乎忽略不计。
• 所有的坐标使用 int 存储，要用时在转化为两维坐标的形式。

CF1468M Similar Sets

我们设阈值为 \(B\)。

我们称集合大小大于 \(B\) 的集合为大集合，否则为小集合。

• 对于大集合，因为只有 \(\frac{n}{B}\) 个，我们可以暴力枚举回答这 \(\frac{n}{B}\) 个大集合。具体的，我们将每个大集合中元素标记为 \(1\)，然后再枚举每个集合，看是否具有至少两个标记即可。时间复杂度：\(\mathcal O(\frac{n}{B}\times n)\)。
• 对于小集合，我们只需处理小集合和小集合的贡献即可。那么我们枚举一个小集合中的二元组，收集其它小集合是否具有这个二元组的标记即可。时间复杂度：\(\mathcal O(B^2 \times \frac{n}{B})\)。证明：因为 \(a^2+b^2 \le (a+b)^2\)，所以最坏情况下肯定不会有集合大小小于 \(B\)，所以复杂度为 \(\mathcal O(B^2 \times \frac{n}{B})\)。

均衡一下，取 \(B=\sqrt{n}\)，即可达到 \(\mathcal O(n \sqrt{n})\) 的优秀复杂度。

P5072 [Ynoi Easy Round 2015] 盼君勿忘

先证明一个引理：假设在一个长度为 \(t\) 的序列中，数字 \(x\) 出现了 \(k\) 次，那么它的贡献就是 \((2^t−2^{t−k})x\)。

证明：考虑容斥。

长度为 \(t\) 的序列的非空子序列有 \(2^t-1\) 个，其中一个 \(x\) 都没包含的非空子序列有 \(2^{t-k}-1\) 个。两者相减即可。

将这个式子推出来之后我就想直接莫队了，却忽略了一个最大难点，那就是随着区间的移动，我们的区间长度是在不断改变的，也就是 \(t\) 其实是不确定的。

所以我们必须将所有贡献以一种形式存储下来，以便莫队移动区间后改变 \(t\) 之后使用。

因为贡献跟出现次数有关，出现次数跟集合和平衡有关，所以考虑根号分治。

注意到一个序列中，出现次数的种类数的个数只有 \(\sqrt{n}\) 个，因为 \(1+2+\dots+\sqrt{n}\) 是在 \(\mathcal O(n)\) 级别的。

我们记录关于出现次数的双向链表，那么根据前面所说，链表大小是在 \(\mathcal O(\sqrt{n})\) 级别的，所以我们只需记链表中每个元素的出现次数 \(x\)，以及原数组中出现次数为 \(x\) 的元素之和即可。

当你信心满满的准备提交时，你发现它每次询问的模数是不固定的！！！，所以每次询问 \(2^k \pmod p\)，你必须用快速幂算，复杂度就带一个 \(\log\)。

我们现在唯一能接受的是在 \(\mathcal O(\sqrt{n})\) 的时间内预处理，\(\mathcal O(1)\) 查询查特定底数的幂 \(2^k \pmod p\)。

有这种算法吗？有的，兄弟有的。我们可以使用一种黑科技——光速幂，它就是一种 \(\mathcal O(\sqrt{n})\) 预处理、\(\mathcal O(1)\) 查询的，求特定底数的幂的快速方法。具体地，我们预处理 \(2^1,2^2,\dots,2^{\sqrt{n}}\) 和 \(2^{\sqrt{n}},2^{2\times \sqrt{n}},\dots,2^{n}\)，然后根据 \(k\) 和 \(\sqrt{n}\) 商和余数即可 \(\mathcal O(1)\) 求出结果。

时间复杂度：\(\mathcal O(n\sqrt{n} \log n)\rightarrow \mathcal O(n\sqrt{n})\)。

CF804D Expected diameter of a tree

首先这道题的期望是假的，我们只需算两棵树 \(x,y\) 中所有连边方式的直径长度和除以 \(siz_x\times siz_y\)。

我们都知道，距离树上一个点最远的点中，一定有一个是直径的端点。所以找出每棵树的直径端点，然后就可以 dfs 求出所有点的最远距离 \(mx_i\)，然后再求出 \(d_x\) 表示 \(x\) 所在树中直径。

考虑两棵树 \(x,y\) 中选择了两个点 \(a,b\) 进行连边，那么直径的长度也可以进行分类讨论，因为新的直径只可能是在 \(x\) 子树中或者在 \(y\) 子树中，再或者在直径就是两棵树合并，即经过了边 \((x,y)\)，长度为 \(mx_a+mx_b+1\)，所以直径为 \(\max(\max(d_x,d_y),mx_a+mx_b+1)\)，左边 \(\max(d_x,d_y)\) 很好处理，难算的是右边 \(mx_a+mx_b+1\) 产生的贡献。

现在不妨设 \(sz_x\le sz_y\)。

一种比较自然的思路是对于 \(x\) 树的每个点 \(t\)，找到 \(y\) 树中所有满足 \(mx_s\ge \max(d_x,d_y)-mx_t\) 的 \(s\) 个数与距离和。注意到 \(mx_s\le sz_y\)，而 \(\sum_y sz_y=n\)，所以可以直接前缀和 \(\mathcal O(n)\) 预处理并 \(\mathcal O(1)\) 回答每个询问。

这样我们回答一次询问的时间复杂度就变为了 \(\min(sz_x,sz_y)\)，因为我们可以枚举结点个数少的那一棵树。如果我们用 map 记忆化所有的询问，总时间复杂度是 \(\mathcal O(n\sqrt{n})\) 的（这里默认 \(n,q\) 同阶）。为什么呢？

考虑将所有树按照大小分为 \(\le \sqrt{n}\) 和 \(> \sqrt{n}\) 两个部分。

• 对于小树和任意树的询问，由于小树的大小 \(\le \sqrt{n}\)，所以总时间复杂度 \(\mathcal O(n\sqrt{n})\)。
• 对于两棵大树之间的询问，因为大树只有 \(\sqrt{n}\) 个，所以这样的询问不会超过 \(\sqrt{n} \times \sqrt{n}=n\) 个，然后对于每个询问我们直接暴力花 \(\sqrt{n}\) 的时间来暴力扫描这棵树回答，

剩余类平衡

对于取模类问题，模数大小与剩余类大小（同余个数）成反比。

算法（剩余类平衡）：

设根号分治阈值为 \(B\)。

• 若模数大小 \(P \le B\)。
  • 模数种类数不超过 \(B\)。
  • 对于 \(\mathcal O(B)\) 种模数使用数据结构维护信息。
• 若模数大小 \(P>B\)。
  • 剩余类种类数较多，同一剩余类大小较小，倍数个数较少。
  • 因此将值域按照模数 \(P\) 分段为 \([0,P-1],[P,2\times P-1],\dots\) 后段数较少。
  • 问题转化为 \(\mathcal O(\frac{V}{B})\) 剩余类段内信息统计。

时间复杂度：

• 设数据结构的操作复杂度为 \(f(x)\)，段内处理时间为 \(g(x)\)。
• 总时间复杂度为 \(\mathcal O(B \times f(x)+\frac{V}{B}\times g(x))\)。

例题

P3396 哈希冲突

按照题意，我们要求的是：

int ans=0;
for(int i=y;i<=n;i+=x)ans+=a[i];

其本质是剩余类平衡，对于模数 \(x\) 我们可以进行分类讨论，从而来进行根号分治。

• 若 \(x\le B\) 时，任何数模 \(x\) 后的种类数只有 \(x\) 种，我们对于每个这样的 \(x\) 用一个桶 \(c_{x,p}\) 记录，表示模 \(x\) 后，余数为 \(p\) 的所有下标的权值和。
• 若 \(x \ge B\) 时，我们可以枚举 \(x\) 的倍数，这样只会有 \(\mathcal O(\frac{V}{B})\) 次枚举。那么我们暴力回答这些询问即可。

时间复杂度：\(\mathcal O(n \sqrt{n})\)。

P9809 [SHOI2006] 作业 Homework

看到不好维护的取模相关信息，想到根号分治。设值域为 \(V\)，根号分治的阈值为 \(B\)。

对于模数不超过 \(B\) 的情况，我们需要利用情况数为 \(O(B)\) 这一性质。在每次插入元素时动态维护所有情况的答案，查询时查表回答即可。

对于模数超过 \(B\) 的情况，我们需要利用商数个数为 \(O(\frac{V}{B})\) 这一性质。使用 set 维护集合中所有元素，每次查询时枚举所有可能的商数，二分查找这种情况下最小可能的余数。

令 \(B=O(\sqrt{V})\) 即可得到 \(O(N\sqrt{V}\log N)\) 的并不优秀的复杂度。

CF103D Time to Raid Cowavans

根号分治+离线卡空间。

这类一步跳多少的题一般都是根号分治。

扩展的说，当变量 \(a\) 和变量 \(b\) 乘积是定值，且既有复杂度关于 \(a\) 的做法又有复杂度关于 \(b\) 的做法的时候，常常采用根号分治平衡复杂度。

在本题，因为跳的步数与跳的长度的积一定（由于步长未必是 \(n\) 的因数，所以不是积严格相等，但是基本相同、一个数量级），如果有一个关于步长的做法、一个关于步数的做法，就可以根号分治完美解决这题。

发现对于 \(k\) 不超过 \(\sqrt n\) 的部分，最多 \(\sqrt n\) 个不同的 \(k\)，可以预处理（起点预处理在 \([0,k-1]\) 即可，不在这个范围就差分求，因为 \(t\) 模 \(k\) 的余数一定在这个范围）。对于超过 \(\sqrt n\) 的部分，暴力模拟跳，最多 \(\sqrt n\) 步。

但是发现预处理的空间开不下。原因是对于每个不超过 \(\sqrt n\) 的步长都开一个前缀和数组的话需要 \(\mathcal O(n \sqrt n)\) 的空间，才能满足每次在线的查询。

考虑将询问离线，按照 \(k\) 排序，对于所有不超过 \(\sqrt n\) 的 \(k\) 预处理一次，然后把所有 \(k\) 值等于当前预处理的 \(k\) 值的询问的答案全部求出。每次只需要一个前缀和数组，空间复杂度降到 \(O(n)\)，时间复杂度仍是 \(\mathcal O(n\sqrt n)\)。

P5309 [Ynoi2011] 初始化

思路：

我们考虑分块维护块内的和。

本题难点主要在修改操作：

• 操作一：将编号为 \(y,y+x,y+2\times x,\cdots,y+k\times x\) 的星星亮度增加 \(z\)。

对于 \(x\ge\operatorname{SIZE}\)（\(\operatorname{SIZE}\) 是块的大小，约为 \(\sqrt{n}\)），由于需要修改的位置不超过块数（约为 \(\sqrt{n}\)），我们直接暴力修改即可。

对于 \(x\lt\operatorname{SIZE}\)，我们不能直接修改，考虑其他方法：

因为亮度变化在整个星星序列内是周期性的，我们可以统计长度为 \(x\) 的周期中，每一个位置的累计修改总和。但是这种方法在查询的时候耗费时间极多，因此我们需要优化。容易想到通过前后缀和可以解决单点改、区间查的问题，我们统计修改的前后缀和即可。

• 操作二：查询 \(\displaystyle\sum_{i=l}^ra_i\)，其中 \(a_i\) 表示亮度。

对于两侧的不完整块，我们直接暴力统计即可。

对于中间的完整块，我们按照块来统计即可。

等等，不要忘记前面统计的前后缀和！在得到按块统计的结果后，我们需要将结果加上对于每一个周期长度，根据前后缀和统计出的累计修改总和。

P6371 [COCI 2006/2007 #6] V

本题要用到一种臭名昭著美名远扬的算法——数据点分治！

相信拿到这题的你一定是通过 数位 dp 标签点进来的吧！所以我们先说这一部分解法。朴素地，设 \(f_{pos,sum,lim,pre}\) 表示当前到第 \(i\) 位时数字和 \(\bmod x = sum\)，此时上限状态为 \(lim\)，前导零状态为 \(pre\)。按 数位 dp 的常规思路，可以得到下面的代码：

int dfs(int pos,int sm,bool lim,bool pre){
	if(f[pos][sm][lim] != -1 && !pre) return f[pos][sm][lim];//记忆化搜索
	if(pos == 1) return sm == 0;
	int up = lim ? num[pos-1] : 9,ans = 0;//确定上限
	for(int i = 0;i <= up;i ++){
		if(i == 0 && pre) ans += dfs(pos-1,sm,0,1);
		if(c[i] && (i != 0 || !pre)) ans += dfs(pos-1,(sm*10 + i) % x,lim && i == up,pre && i == 0);
      //特别注意对 0 的处理，小心漏算和重算
	}
	if(!pre) f[pos][sm][lim] = ans;
	return ans;
}

我们发现这样的做法只能解决 \(X \le 10^5\) 的情况，再大就会内存超限。

那么对于 \(10^5 \le X \le 10^{11}\) 怎么办呢？其实更简单，我们采用暴力枚举！这样最多计算 \(10^6 \times 11 = 1.1 \times 10^7\) 次，可以 AC 本题。

【后记】

注意到进行数位 dp 时，没有采取常规的方法将 \(pre\) 作为数组一维，这是因为丧心病狂的出题人空间开的太小，会爆掉！

CF484B Maximum Value

• 方法一：平衡规划——剩余类平衡

严格 \(\mathcal O(n\sqrt{V})\) 的做法。

根号分治，记 \(V=\max a_i\)，阈值为 \(B\)。

对于 \(a_i>B\)，形如 \([Ka_i,(K+1)a_i)\) 的段不超过 \(\frac{V}{B}\) 个，每个段取最大的数最优，考虑预处理 \(pre_i\) 表示 \(\le i\) 的数的最大值，那么这一部分可以做到 \(O(\frac{m}{B})\)。

对于 \(a_i\le B\)，\([a_i,2a_i)\) 段长不超过 \(B\)，可以枚举枚举其中每一个数 \(j\)，若存在 \(a_k=x\ge a_i\) 满足 \(x\bmod a_i=j-a_i\)，那么 \(j\) 合法。考虑预处理 \(d_{i,j}\) 表示是否存在一个 \(a_k=x\) 满足 \(x\bmod i=j\) 即可做到 \(O(B)\) 处理。

当 \(B=\sqrt{V}\) 时取到最优复杂度 \(O(n\sqrt{V})\)。

• 方法二：枚举倍数+二分

我们知道 \(a \mod\ b\) 可以化成 \(a-kb\)（\(a,b,k\) 都是整数，\(k=\left\lfloor\dfrac{a}{b}\right\rfloor\)）的形式。

于是可以发现 \(kb\le a<(k+1)b\)。

那么就先枚举 \(k\) 和 \(b\)，因为 \(a<(k+1)b\)，所以可以二分最大的符合条件的 \(a\)，取最大的 \(a \mod \ b\) 的值即可。

于是可以轻松过掉此题。

CF446C DZY Loves Fibonacci Numbers

三个做法。

Solution 1：操作序列分块

设阈值为 \(B\)。

每隔 \(B\) 个操作就把这些操作用 \(\mathcal O(n)\) 的时间更新到原序列中。那么复杂度为 \(\mathcal O(\frac{n^2}{B}+nB)\)。因为残存的 \(B\) 个操作我们每次询问的时候暴力询问这些操作带来的影响即可。

Solution 2：fibonacci 的一个性质：\(f_{n+m}=f_{n+1}f_{m}+f_{n}f_{m-1}\)。

我们看一个操作 \([l,r]\) 的具体影响，即 \(x\in[l,r]\) 都加了 \(f_{x-l+1}\)，将它展开我们可以得到：\(f_{x-l+1}=f_{x+1}f_{-l+1}+f_{x}f_{-l}\)。

所以我们查询每个区间答案时，只需要知道 \(f_{l+1}+f_{l+2}+\dots+f_{r+1}\) 和 \(f_l+f_{l+1}+\dots +f_r\) 值即可。这个我们可以轻而易举的预处理出来。那么修改时就可以很简单下传 pushdown 的标记了。

时间复杂度：\(\mathcal O(n \log n)\)。

Solution 3：fibonacci 的另一个性质（广义 fibonacci 数列）：\(s_{1}=a,s_2=b,s_i=a\times f_{i-2}+b\times f_{i-1}\)。 \(\sum_{i=1}^n s_i=s_{n+2}-s_2\)。而且两个广义 fibonacci 数列对应项相加还是广义 fibonacci 数列，原因显然。

那么对每个区间实时维护 \(s_1,s_2\) 即可。即一次修改 \([l',r']\in [l,r]\)，会使 \([l',r']\) 的 \(s_1,s_2\) 增加 \(f_{l'-l+1},f_{l'-l+2}\)。

下传标记时也可以直接下传。

时间复杂度：\(\mathcal O(n \log n)\)。

二进制平衡

对于状压或者二进制位相关的题目，状态数量为 \(2^n\)。

此时，如果修改和查询均对所有状态执行，那么时间复杂度无法接受。

考虑平衡修改和查询的复杂度，通过修改时预处理部分信息优化查询时间。

而值域的根号分治=二进制的高位和低位。

因此，对于二进制相关的问题，可以使用根号分治对和高位和低位分别处理——二进制平衡。

例题

4788 -- 【2016NOI十连赛5-1】二进制的世界

前缀位运算最值统计。

考虑朴素算法：

• 值域较小，\(a_i \le 2^{16}\)，考虑使用桶维护前缀元素个数。
• 修改 \(\mathcal O(1)\)，查询 \(\mathcal O(V)\)。

修改和查询时间复杂度不平衡，且与二进制值域有关，考虑二进制平衡规划。使用根号分治。

以 \(B=\frac{\log_{2} V}{2}\) 作为阈值，此时任意元素分为高位和低位两段。

考虑在修改时预处理部分信息以均衡查询时间复杂度。

要求位运算最大值，因此查询时贪心保证高位大。

高位状态仅为 \(\mathcal O(2^B)\)，因此可以在修改时预处理元素的不同高位 \(S_1\) 时 opt 的操作最值 \(f_{S_1}\)。

但是高位相同时需要保证低位大，因此 opt \(S_1\) 相同时，元素低位不同，最后的答案就不同，有后效性。

因此设 \(f_{S_1,S_2}\) 表示查询元素高位为 \(S_1\)，修改元素低位为 \(S_2\) 的最大值。

直接更改即可。

时间复杂度：\(\mathcal O(2^B \times V)=\mathcal O(V \sqrt{V})\)。

分治树整体DP

点分治

例题

P3806 【模板】点分治 1

树上静态路径问题，考虑点分治。

考虑点分治时的点分中心 \(rt\)，这题二叉合并和容斥方法都可以做。

先考虑容斥。算出所有点到 \(rt\) 的距离，存储在 \(dis\) 数组中。将 \(dis\) 排序，对于每个询问 \(q_i\)，双指针扫描一遍 \(dis\) 数组，如果 \(dis_l+dis_r\) 的值为 \(q_i\)，且 \(l\) 和 \(r\) 所指的点不在同一个子树中，则对于 \(q_i\) 的答案为真。

时间复杂度：\(\mathcal O(n\log^2 n+nm\log n)\)。

鉴于本题是模板题，故放出核心代码：

void get_dis(int u,int fa,int dis,int fr)
{
	a[++tot]=u;
	d[u]=dis;
	b[u]=fr;
	for(int i=head[u];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==fa||vis[v])continue;
		get_dis(v,u,dis+e[i].w,fr);
	}
}
void calc(int u)
{
	tot=0;
	a[++tot]=u;
	d[u]=0;
	b[u]=u;
	for(int i=head[u];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(vis[v])continue;
		get_dis(v,u,e[i].w,v);
	}
	sort(a+1,a+1+tot,cmp);
	for(int i=1;i<=m;i++)
	{
		int l=1,r=tot;
		if(mark[i])continue;
		while(l<r)
		{
			if(d[a[l]]+d[a[r]]>q[i])r--;
			else if(d[a[l]]+d[a[r]]<q[i])l++;
			else if(b[a[l]]==b[a[r]])
			{
				if(d[a[r]]==d[a[r-1]])r--;
				else l++;
			}
			else{mark[i]=true;break;}
		}
	}
}
void solve(int u)
{
	vis[u]=true;
	calc(u);
	for(int i=head[u];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(vis[v])continue;
		root=0;
		get_root(v,u,sz[v]);
		solve(root);
	}
}

P4149 [IOI 2011] Race

树上静态路径问题，考虑点分治。

考虑当前点分中心 \(rt\)，考虑二叉合并。当遍历 \(rt\) 的一个子树 \(u\) 时，对于 \(u\) 子树中每一个点预处理出到 \(rt\) 的权值和 \(dis_x,x\in \text{subtree}(u)\)。对于之前遍历过的子树 \(v_1,v_2,\dots.v_k\) 和 \(rt\) 本身，我们计算 \(u\) 子树与遍历过的子树和 \(rt\) 的贡献，具体地，对于 \(u\) 子树中的一个点 \(x\)，我们需要计算其他子树到 \(rt\) 距离为 \(k-dis_x\) 的点是否存在，如存在其边的数量最少是多少，因为 \(k\le 10^6\)，所以这部分我们用一个桶来维护即可。即记 \(len_i\)，表示权值和为 \(i\) 的路径的最少边数是多少。注意因为要把 \(rt\) 算进去，我们可以直接设 \(len_0=0\)。

时间复杂度：\(\mathcal O(n \log n)\)。

P2993 [FJOI2014] 最短路径树问题

强行二合一（双倍经验？）。

第一步，先建出最短路径树，由于要建字典序最小的，那么我们先求出所有可能在最短路径树上的边，然后我们再对 \(u\) 的所有可能在最短路径树上的边进行排序，然后依次递归建树即可。

第二步，建完树后，我们考虑如何统计答案。

树上静态路径问题，考虑点分治。

问题转化为求树上点分治经典问题（实际上就是套用上道题的思路）。就不讲了。

时间复杂度：\(\mathcal O(n \log n)\)。

P2634 [国家集训队] 聪聪可可

人话：求所有树上路径长度为 \(3\) 的倍数的数量。

树上静态路径问题，考虑点分治。

首先树上总路径条数为 \(n^2\)。

然后考虑当前分治中心 \(rt\)，这个问题我们考虑用容斥的方法做。先对于当前子树 \(u\)，预处理出 \(u\) 的子树中所有节点 \(x\) 到 \(rt\) 的距离 \(d~\text{mod}~3\) 的值为 \(dis_x\)，再开一个桶 \(tong_{0/1/2}\) 表示 \(dis_x\) 是 \(0/1/2\) 的个数。答案就为 \(tong_0\times tong_0+tong_1 \times tong_2 \times 2\)，表示路径 \(\text{mod}~3\) 为 \(0\) 的路径端点可以随便组合，然后另外一种情况则是选出来的方案可以端点互换。

时间复杂度：\(\mathcal O(n \log n)\)。

2764 -- 【POJ1741-BZOJ1468】树中点对统计

树上静态路径问题，考虑点分治。

然后考虑当前分治中心 \(rt\)，这个问题我们考虑用容斥的方法做。先对于当前子树 \(u\)，预处理出 \(u\) 的子树中所有节点 \(x\) 到 \(rt\) 的距离为 \(dis_x\)。将 \(dis\) 数组从小到大排序后，双指针扫一遍即可。记得要容斥。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

P4178 Tree

双倍经验。

CF293E Close Vertices

树上静态路径问题，考虑点分治。

然后考虑当前分治中心 \(rt\)，这个问题我们考虑用容斥的方法做。先对于当前子树 \(u\)，预处理出 \(u\) 的子树中所有节点 \(x\) 到 \(rt\) 的距离为 \(dis_x\)，还有到 \(rt\) 的深度。将 \(dis\) 数组从小到大排序后。此题就变为了二维数点问题，即有多少给点对 \((u,v)\) 满足 \(dis_u+dis_v\le w,dep_u+dep_v\le l\)。

双指针扫一遍扫描线维护距离 \(dis\) 这一维，然后用树状数组维护 \(dep\) 这一维即可。记得要容斥。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

3728 -- 【BZOJ3784】树上路径

树上静态路径问题，考虑点分治。

问题转化为求树上路径第 \(k\) 小，求第 \(k\) 小一般有两个思路——\(k\) 路归并和二分。

一般是当 \(k\) 较小时才可考虑 \(k\) 路归并，而本题恰好 \(k\) 较小，很适合 \(k\) 路归并。那么我们设当前点分中心为 \(rt\)，现在我们考虑是用二叉合并还是容斥的方式来计算最终答案。对于最优化问题，一般使用二叉合并来维护，所以考虑合并两个子树的过程：当 \(v_k\) 和 \(rt,v_1,v_2,\dots.v_{k-1}\) 合并时，会产生哪些影响。

那么我们先求出所有点到 \(rt\) 的距离 \(dis_x\)，再对所有 \(dis\) 从大到小排个序，那么我们类似 \(k\) 路归并的方式，先把对于排序后的数组中的一个下标 \(i\)，找到他往后第一个跟它不在一个子树的点 \(nxt_i\)，把 \(dis_i+dis_{nxt_i}\) 放入大根堆 \(q\) 里面。那么进行 \(k\) 路归并时，每次取出一个堆顶时与答案小根堆 \(ans\) 进行比较，如果大于，则取出 \(ans\) 的堆顶，放入 \(q\) 的堆顶，其实这就是 \(k\) 路归并算法。取出以后再将 \(dis_i+dis_{nxt_i+1}\) 放进去（如果 \(nxt_i+1\) 和 \(i\) 不在同一个子树里），否则我们就把 \(dis_i+dis_{nxt_{nxt_i+1}}\) 放进去。

那么这个 \(k\) 路归并的时间复杂度是多少呢？分治是一共要分治 \(\mathcal O(n \log n)\) 次，每次更新答案需要 \(\mathcal O(k \log n)\) 的时间，那么总复杂度就是 \(\mathcal O(nk\log^2 n)\) 的时间过不了，考虑优化。（但是实际上这样写是可以过掉这道题的，只不过数据太水）

现在感觉做不了，但是我们先引入一个题目：P2048 [NOI2010] 超级钢琴

这道题让你求出前 \(k\) 大的『和弦』，那么一个『和弦』肯定能表示为一个三元组 \((i,l,r)\) 表示 \(j\in [i+l-1,i+r-1]\)，\([i,j]\) 这个区间都能成为答案。那么我们肯定是选取值最大的，即 \(sum_j-sum_{i-1}\) 使得这个值最大的 \(j\)，即 \([i+l-1,i+r-1]\) 中最大的 \(sum_j\)，所以我们记 \((i,l,r,pos)\) 其中 \(i,l,r\) 定义同上，\(pos\) 表示最大的 \(j\)。

那么 \(k\) 路归并时，先取出 \(sum_j-sum_{i-1}\) 最大的点，然后我们就不能再选 \((i,j)\) 这个区间了，但是除了 \(j\) 以外的其它地方还可以选，即 \([i+l-1,j-1],[j+1,i+r-1]\) 这两段区间，所以同样的我们把这两端加入堆中即可。

时间复杂度分析：由于堆顶只会弹出 \(k\) 次，每次弹出放回两个区间，最多放回 \(2\times k\) 个区间，复杂度能过。所以整体复杂度就是 \(\mathcal O(n \log n)\) 的。

那么回到正题。

我们把这棵树的点分治序处理出来。假设我们确定了一个分治中心下的一条链，我们需要找到另一条链使得两条加起来最大。

那么另外一条可行链的端点在点分治序上一定形成一段区间。然后就变成了对于一个右端点都有一段可行的左端点，要求两点权值和最大。

之后就变成了[NOI2010]超级钢琴。点分治序+st表+堆。

时间复杂度：由于点分治序是 \(\mathcal O(n \log n)\) 的，则 st 表预处理需要 \(\mathcal O(n \log^2 n)\)。

代码：

#include <queue>
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
#define MAXIN 300000
//#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=50005,M=N*16;

int Enum,H[N],nxt[N<<1],to[N<<1],len[N<<1],Min,root,sz[N],tot,d[M],L[M],R[M],Ln,Rn,Log[M],pos[20][M];
bool vis[N];
char IN[MAXIN],*SS=IN,*TT=IN;
struct Node
{
	int val,di,l,r;
	bool operator <(const Node &a)const
	{
		return val<a.val;
	}
};
std::priority_queue<Node> q;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-48,c=gc());
	return now;
}
inline void AE(int w,int u,int v)
{
	to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum, len[Enum]=w;
	to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum, len[Enum]=w;
}
inline int Max(int x,int y)
{
	return d[x]>d[y]?x:y;
}
inline int Query(int l,int r)
{
	int k=Log[r-l+1];
	return Max(pos[k][l],pos[k][r-(1<<k)+1]);
}
void FindRoot(int x,int fa,int tot)
{
	int mx=0; sz[x]=1;
	for(int i=H[x],v; i; i=nxt[i])
		if(!vis[v=to[i]] && v!=fa)
			FindRoot(v,x,tot), sz[x]+=sz[v], sz[v]>mx&&(mx=sz[v]);
	mx=std::max(mx,tot-sz[x]);
	if(mx<Min) Min=mx, root=x;
}
void Calc(int x,int fa,int dep)
{
	d[++tot]=dep, L[tot]=Ln, R[tot]=Rn;
	for(int i=H[x],v; i; i=nxt[i])
		if(!vis[v=to[i]] && v!=fa) Calc(v,x,dep+len[i]);
}
void Solve(int x)
{
	vis[x]=1, d[++tot]=0, L[tot]=1, R[tot]=0, Ln=Rn=tot;
	for(int i=H[x]; i; i=nxt[i])
		if(!vis[to[i]]) Calc(to[i],x,len[i]), Rn=tot;
	for(int i=H[x]; i; i=nxt[i])
		if(!vis[to[i]]) Min=N, FindRoot(to[i],x,sz[to[i]]), Solve(root);
}

int main()
{
	const int n=read(),m=read();
	for(int i=1; i<n; ++i) AE(read(),read(),read());
	Min=N, FindRoot(1,1,n), Solve(root);

	pos[0][1]=1;
	for(int i=2; i<=tot; ++i) Log[i]=Log[i>>1]+1, pos[0][i]=i;
	for(int j=1; j<=Log[tot]; ++j)//写成 j<=Log[n],i=n-t，还能过除了第6个点外的所有点= =。
		for(int t=1<<j-1,i=tot-t; i; --i)
			pos[j][i]=Max(pos[j-1][i],pos[j-1][i+t]);
	for(int i=1; i<=tot; ++i)
		if(L[i]<=R[i]) q.push((Node){d[i]+d[Query(L[i],R[i])],d[i],L[i],R[i]});

	for(int i=1,p; i<=m; ++i)
	{
		Node tmp=q.top(); q.pop();
		printf("%d\n",tmp.val), p=Query(tmp.l,tmp.r);
		if(tmp.l<p) q.push((Node){tmp.di+d[Query(tmp.l,p-1)],tmp.di,tmp.l,p-1});
		if(p<tmp.r) q.push((Node){tmp.di+d[Query(p+1,tmp.r)],tmp.di,p+1,tmp.r});
	}

	return 0;
}

P3060 [USACO12NOV] Balanced Trees G

树上静态路径问题，考虑点分治。

怎么说呢，这题多画画图就行了，本质上不难，分类讨论最重要。

时间复杂度：\(\mathcal O(n \log n)\)。

5889 -- 【bzoj3697】采药人的路径

树上静态路径问题，考虑点分治。

括号序列，明显先转为 \(01\) 序列来做，并设 \(d_x\) 表示到当前分治中心 \(rt\) 的路径边权权值和。

考虑分治中心 \(rt\)，答案的贡献就是有两个点存在于 \(rt\) 的不同的两棵子树中。且 \(x\) 到 \(y\) 的路径权值和为 \(0\)，存在一个点 \(z\ne x,y\)，使得在 \(x\) 到 \(rt\) 的路径上 \(d_x=d_z\)，或者 \(y\) 到 \(rt\) 的路径上 \(d_y=d_z\)。这个很显然可以分类讨论， 那么我们可以记 \(f_{i,0/1}\) 表示前面的子树中深度为 \(i\) ，不存在/存在它到当前分治中心路径上的一个点，使得它的深度 \(=i\) 的点的个数。

考虑对于当前深度为 \(d\) 的点 \(x\)，显然至少有 \(f_{-d,1}\) 个点会和 \(x\) 形成一条合法的路径。 如果分治中心到 \(x\) 的路径上存在一个深度为 \(d\) 的点，那么还会有 \(f_{-d,0}\) 个点会和 \(x\) 形成一条合法路径。

代码：

#include<bits/stdc++.h>
using namespace std;
#define MAXN 200010
typedef long long LL;
const int inf = 2e9;
struct edge
{
        int to , w , nxt;
} e[MAXN << 1];
int n , tot , root , len;
int head[MAXN] , size[MAXN] , weight[MAXN] , cnt[MAXN << 1];
int s[MAXN << 1][2];
bool visited[MAXN];
LL ans;
template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); }
template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); }
template <typename T> inline void read(T &x)
{
    T f = 1; x = 0;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + c - '0';
    x *= f;
}
inline void addedge(int u,int v,int w)
{
        tot++;
        e[tot] = (edge){v , w , head[u]};
        head[u] = tot;
}
inline void getroot(int u , int fa , int total)
{
        weight[u] = 0;
        size[u] = 1;
        for (int i = head[u]; i; i = e[i].nxt)
        {
                int v = e[i].to;
                if (v == fa || visited[v]) continue;
                getroot(v , u , total);
                size[u] += size[v];
                chkmax(weight[u] , size[v]);
        }        
        chkmax(weight[u] , total - size[u]);
        if (weight[u] < weight[root]) root = u;
}
inline void calc(int u , int fa , int dep)
{
        ans += s[n - dep][1];
        if (cnt[n + dep] > 0) ans += s[n - dep][0];
        if (dep == 0 && cnt[n] > 1) ++ans;
        ++cnt[n + dep];
        for (int i = head[u]; i; i = e[i].nxt)
        {
                int v = e[i].to , w = e[i].w;
                if (v == fa || visited[v]) continue;
                calc(v , u , dep + w);        
        } 
        --cnt[n + dep];
}
inline void update(int u , int fa , int dep)
{
        ++s[n + dep][cnt[n + dep] > 0];
        ++cnt[n + dep];
        for (int i = head[u]; i; i = e[i].nxt)
        {
                int v = e[i].to , w = e[i].w;
                if (v == fa || visited[v]) continue;
                update(v , u , dep + w);
        }
        --cnt[n + dep];
}
inline void clear(int u , int fa , int dep)
{
        size[u] = 1;
        --s[n + dep][cnt[n + dep] > 0];
        ++cnt[n + dep];
        for (int i = head[u]; i; i = e[i].nxt)
        {
                int v = e[i].to , w = e[i].w;
                if (v == fa || visited[v]) continue;
                clear(v , u , dep + w);
                size[u] += size[v];
        }
        --cnt[n + dep];
}
inline void work(int u)
{
        visited[u] = true;
        cnt[n] = 1;
        for (int i = head[u]; i; i = e[i].nxt)
        {
                int v = e[i].to , w = e[i].w;
                if (visited[v]) continue;
                calc(v , u , w);
                update(v , u , w);        
        }        
        for (int i = head[u]; i; i = e[i].nxt)
        {
                int v = e[i].to , w = e[i].w;
                if (visited[v]) continue;
                clear(v , u , w);
        }
        for (int i = head[u]; i; i = e[i].nxt)
        {
                int v = e[i].to;
                if (visited[v]) continue;
                root = 0;
                getroot(v , 0 , size[v]);
                work(root);
        }
}

int main()
{
        
        read(n);
        for (int i = 1; i < n; i++)
        {
                int u , v , w;
                read(u); read(v); read(w);
                w = (w == 0) ? -1 : 1;
                addedge(u , v , w);
                addedge(v , u , w);
        }
        weight[root = 0] = inf;
        getroot(1 , 0 , n);
        work(root);
        printf("%lld\n",ans);
        return 0;
    
}

P5306 [COCI 2018/2019 #5] Transport

树上静态路径问题，考虑点分治。

考虑当前分治中心 \(rt\)，这个路径统计可以使用容斥的方法来做（后面会说），对于两个子树 \(u\) 和 \(v\) 中的点 \(x,y\)，满足 \(x\) 能到达 \(y\) 的条件为：\(x\) 能到达 \(rt\)，\(rt\) 能到达 \(y\)。

设 \(dis_u\) 表示 \(u\) 到 \(rt\) 的路径上的权值和，\(sum_u\) 表示 \(u\) 到 \(rt\) 路径上所有点 \(a\) 值的和。

先考虑第一部分，\(x\) 能到达 \(rt\) 意味着对于 \(x\) 到 \(rt\) 的路径上任意一点 \(j\)，都有 \(sum_x-sum_j\ge dis_x-dis_j\)，变个形式为 \(sum_x-dis_x\ge sum_j-dis_j\) 那么我们找到路径上最大的 \(sum_j-dis_j\) 就行了，注意这个东西可以在遍历时就把不满足这个条件的 \(x\) 给去除掉。

再考虑第二部分，\(rt\) 能到达 \(y\) 一位置对于 \(rt\) 到 \(y\) 的路径上任意一点 \(j\)，都有 \(R+sum_{fa_j}-dis_j\ge 0\)，其中 \(R\) 表示 \(x\) 到 \(rt\) 还有多少油（不算 \(rt\) 这个点的油，也就是 \(sum_x-dis_x-a_{rt}\)），变个形式为 \(R+(sum_{fa_j}-dis_j)\ge 0\)，我们只需找到路径上最小的 \(sum_{fa_j}-dis_j\) 就行了。

我们统计路径条数就可以先分别按照 \(sum_j-dis_j\) 和 \(sum_{fa_j}-dis_j\) 从小到大排个序，然后双指针计算方案数即可。即令 \(j=r,i=l\)，只要 \(sum_j-dis_j+(sum_{fa_i}-dis_i)-a_{rt}\ge 0\) 即可。可以看见这个明显容斥会好做一点。

时间复杂度：\(\mathcal O(n \log n)\)。

边分治

笛卡尔分治树

个人感觉和笛卡尔树启发式合并差不多，只不过是用分治来模拟笛卡尔树的建树过程。

详细请见 笛卡尔树启发式合并。

启发式合并

笛卡尔树启发式合并

同树链剖分的复杂度分析，都是 \(\mathcal O(n \log n)\)。

CF1156E The Number of Subpermutations

Algorithm 1：笛卡尔树启发式合并+set

枚举 \(l\)，求 \(r\) 的扫描线在这题不好求，考虑枚举最小值 \(mn\)。令 \(pos_l,pos_r\) 分别表示从 \(i\) 开始从左往右第一个小于 \(p_i\) 的位置/从左往右第一个小于 \(p_i\) 的位置。然后对应到笛卡尔树上求相当于 \(ls,rs\)，则枚举 \(sz\) 较小的一个子树，然后再合并，边合并边用 set 将每个元素加入其中，询问 \(p_i-a_{now}\) 的值是否存在即可。

时间复杂度：\(\mathcal O(n \log^2n)\)。

Algorithm 2：笛卡尔树启发式合并

因为这个算法和点在笛卡尔树上的祖先顺序无关，所以可以直接从左往右枚举 \(i\)。

先预处理出 \(\operatorname{lmn}(i),\operatorname{rmn}(i)\) 。

因为此题是排列，可以 \(\mathcal O(1)\) 得到一个数的具体位置，所以就不用 set，这样就少了个 \(\log\)。

时间复杂度：\(\mathcal O(n \log n)\)。

int n,a[200005],b[200005];
int lm[200005],rm[200005],st[200005],top;
inline void init(){
	a[0]=1e9,st[top=1]=0;
	rep(i,1,n){
		while(top&&a[st[top]]<a[i])top--;
		lm[i]=st[top];
		st[++top]=i;
	}
	a[n+1]=1e9,st[top=1]=n+1;
	per(i,1,n){
		while(top&&a[st[top]]<a[i])top--;
		rm[i]=st[top];
		st[++top]=i;
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;
	rp(i,n)cin>>a[i];
	rp(i,n)b[a[i]]=i;
	init();
	int ans=0;
	rp(i,n){
		int l=lm[i]+1,r=rm[i]-1;
		if(l<i&&i<r){
			if(r-i>i-l)rep(j,l,i-1){
				int to=b[a[i]-a[j]];
				ans+=(i<to&&to<=r);
			}else rep(j,i+1,r){
				int to=b[a[i]-a[j]];
				ans+=(l<=to&&to<i);
			}
		}
	}
	cout<<ans<<endl;
	return 0;
}

Algorithm 2：分治模拟笛卡尔树，每次 \(\operatorname {solve}(l,r)\)。

用 st 表预处理出 \([l,r]\) 中最小值出现位置 \(mid\)，找到当前区间的子树的根。然后统计跨越 \(mid\) 的贡献，即 \([l,mid-1]\) 和 \([mid+1,r]\) 之间的贡献。这个就和笛卡尔树上的子树是一样的了，启发式合并可以做到 \(\mathcal O(n \log n)\)。这种做法的优点为可以拓展，比起前两种做法更好，既有笛卡尔树的分治，也有从左往右扫描的简洁。

CF1175F The Number of Subpermutations

此题就只能用到上一道题的第三种解法。

具体地，当一个子区间 \([l,r]\) 是子排列时，当且仅当满足一下条件：

1. 区间元素不重复。
2. 区间最小值为 \(1\)。
3. 区间最大值为 \(r-l+1\)。

发现上面三个条件只需满足1和3即可自动满足2了。考虑如何处理“区间元素不重复这一限制条件”。

我们发现如果 \([l,r]\) 没有元素重复，则有 \(pre_i<l,\forall i \in[l,r]\)，但因为 \(pre_i<i\) ，所以设 \(f_i=\max_{j=1}^i pre_j\)。则判别式为 \(f_r<l\)。所以按照上一道题，根据最大值分治，用分治模拟建笛卡尔树的过程，启发式合并如果 \(mid-l<r-mid\)，则枚举 \(i\in[l,mid]\)，则右端点已经确定为 \(j=i+a_{mid}-1\)，判断一下第一个条件 \(f_j<i\) 是否成立即可。

时间复杂度：\(\mathcal O(n\log n)\)。

const int N=3e5+50,M=2e6+50,inf=2e9,mod=998244353;
int n,ans;
int a[N],LG[N],st[22][N],f[N],g[N],pre[N],nxt[N];
int cmp(int x,int y){return a[x]>=a[y]?x:y;}
int query(int l,int r)
{
	int k=LG[r-l+1];
	return cmp(st[k][l],st[k][r-(1<<k)+1]);
}
void solve(int l,int r)
{
	if(l>r)return;
	if(l==r)
	{
		ans+=(a[l]==1);
		return;
	}
	int mid=query(l,r);
	if(mid-l<r-mid)
	{
		for(int i=l;i<=mid;i++)
		{
			int j=a[mid]+i-1;
			if(j>r||j<mid||g[i]<=j)continue;
			ans++;
		}
	}
	else
	{
		for(int i=mid;i<=r;i++)
		{
			int j=i-a[mid]+1;
			if(j<l||j>mid||f[i]>=j)continue;
			ans++;
		}
	}
	solve(l,mid-1);solve(mid+1,r);
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;LG[0]=-1;
	for(int i=1;i<=n;i++)cin>>a[i],LG[i]=LG[i>>1]+1,st[0][i]=i;
	for(int j=1;j<=21;j++)
		for(int i=1;i+(1<<j)-1<=n;i++)
			st[j][i]=cmp(st[j-1][i],st[j-1][i+(1<<(j-1))]);
	for(int i=1;i<=n;i++)
	{
		f[i]=max(f[i-1],pre[a[i]]);
		pre[a[i]]=i;nxt[i]=n+1;
	}g[n+1]=n+1;
	for(int i=n;i>=1;i--)
	{
		g[i]=min(g[i+1],nxt[a[i]]);
		nxt[a[i]]=i;
	}
	solve(1,n);
	cout<<ans<<endl;
	return 0;
}

HDU6701 Make Rounddog Happy

通过阅读题意，发现好数组的性质为：

1. 元素不重复。
2. \(r-l+1 \ge -k+\max_{i=l}^r a_i\)。

直接套用上一道题解法即可。

const int N=3e5+50,M=2e6+50,inf=2e9,mod=998244353;
int T,n,k,ans;
int a[N],LG[N],st[22][N],f[N],g[N],pre[N],nxt[N];
int cmp(int x,int y)
{
//	cout<<x<<" "<<y<<" "<<a[x]<<" kkkkkkkkkk "<<a[y]<<endl;
	if(a[x]>=a[y])return x;
	return y;
}
int query(int l,int r)
{
	int k=LG[r-l+1];
	return cmp(st[k][l],st[k][r-(1<<k)+1]);
}
void solve(int l,int r)
{
	if(l>r)return;
	if(l==r)
	{
		if(a[l]-1<=k)ans++;
		return;
	}
	
	int mid=query(l,r);
	int tmp=a[mid]-k;
	if(mid-l<r-mid)
	{
		for(int i=l;i<=mid;i++)
		{
			int j=i+tmp-1,k=g[i]-1;
			j=max(j,mid);k=min(k,r); 
			if(j<=k)ans+=k-j+1;
		}
	}
	else
	{
		for(int i=mid;i<=r;i++)
		{
			int j=i-tmp+1,k=f[i]+1;
			j=min(j,mid);k=max(k,l);
			if(k<=j)ans+=j-k+1;
		}
	}
	solve(l,mid-1);solve(mid+1,r);
}
void sol()
{
	cin>>n>>k;ans=0;
	for(int i=1;i<=n;i++)cin>>a[i],st[0][i]=i,pre[i]=0,nxt[i]=n+1;
	for(int j=1;j<=21;j++)
		for(int i=1;i+(1<<j)-1<=n;i++)
			st[j][i]=cmp(st[j-1][i],st[j-1][i+(1<<(j-1))]);
	for(int i=1;i<=n;i++)
	{
		f[i]=max(f[i-1],pre[a[i]]);
		pre[a[i]]=i;
	}g[n+1]=n+1;
	for(int i=n;i>=1;i--)
	{
		g[i]=min(g[i+1],nxt[a[i]]);
		nxt[a[i]]=i;
	}
	solve(1,n);
	cout<<ans<<endl;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>T;
	LG[0]=-1;
	for(int i=1;i<=N-20;i++)LG[i]=LG[i>>1]+1;
	while(T--)sol();
	return 0;
}

P4755 Beautiful Pair

和上一道题一模一样，用分治模拟建笛卡尔树。

问题关键在统计 \([l,r]\) 中有多少 \(a_i \times a_j\le a_{mid}\)，即有多少 \(a_j\le \frac{a_{mid}}{a_i}\)。

将这些询问统计下来，最后用差分做 \(\Delta t=[1,r]-[1,l-1]\)，所以类似二离莫队，最后用扫描线回答这些询问即可。

时间复杂度：\(\mathcal O(n\log^2 n)\)。

Trie 合并

例题

CF965E Short Code

有趣题。

不难想到把 \(n\) 个字符串都放到 Trie 上维护，这样问题就转化为了：对于一棵有若干个结点的树，其中一些结点上有一个球，每次可以把球移动至它到根结点的路径中没有球的结点上，问最终所有球的深度之和的最小值。

可以考虑对每个结点维护一个大根堆，记录其子树内球的深度。合并子树时，只需要把其每个子结点的大根堆进行启发式合并即可。同时，如果根结点上没有球，可以贪心地把子树内深度最深的球移动至根结点上，正确性显然。

答案即为 Trie 的根结点的大根堆中所有元素之和。要注意需要特殊处理 Trie 的根结点，不能把球移到 Trie 的根结点上。

每个黑点 \(x\) 会被计算 \(dep_x\) 次，而 \(∑dep_x=n\)。

时间复杂度：\(\mathcal O(n \log n)\)。

CF778C Peterson Polyglot

考虑 \(\text{trie}\) 树合并的复杂度到底是什么？

不难发现，合并时每遍历到一个节点，这个点必然同时在两棵树中出现，所以不难发现的是合并大小为 \(sz_a,sz_b\) 的 \(\text{trie}\) 树复杂度为 \(\min(sz_a,sz_b)\)。

于是在枚举断掉哪一层的节点时，考虑直接将所有儿子依次合并，并计算出带来的贡献，这个过程时间复杂度等价于启发式合并，因此是 \(\mathcal O(n\log n)\) 的。

关键代码：

inline int merge(int x, int y) {
  if (x == 0 || y == 0) 
    return x + y;
  int now = ++cnt;
  for (int i = 0; i < 26; i++)
    son[now][i] = merge(son[x][i], son[y][i]);
  return now;
}

inline void dfs(int now, int deep) {
  int num;
  num = cnt = n + 1;
  for (int i = 0; i < 26; i++)
    if (son[now][i])
      num = merge(num, son[now][i]);
  sum[deep] += cnt - n - 1;
  for (int i = 0; i < 26; i++)
    if (son[now][i]) dfs(son[now][i], deep + 1);
}

Set/平衡树 合并

例题

#516. 「LibreOJ β Round #2」DP 一般看规律

这道题要求每个数的前驱和后继，所以用平衡树（set）来维护。我们对每个颜色开一个 set，然后查询时直接在 set 里二分一下即可。考虑两个颜色的合并操作，所有 \(x\) 变为 \(y\) 这个操作说明了只能合并而不能分裂。也就是说一开始有若干个集合，它们的大小总和为 \(n\)，现在有一些操作，要求把 \(x\) 集合和 \(y\) 集合合并起来，一共最多有 \(m\) 合并操作，所以考虑启发式合并，每次合并颜色集合大小较小的那个集合即可，这样每个元素最多被合并 \(\log\) 次，这样复杂度为 \(\mathcal O(n \log^2 n)\)。

P4416 [COCI 2017/2018 #1] Plahte

给定 \(n\) 个互不相交，可以重叠的矩阵，对某些点染色，这个点上的所有矩阵会被染上这个颜色，求最后每个矩阵会有多少种颜色。

引理： 对于任意个几何图形，若他们间只存在包含或相邻关系，那么他们可以构成一个森林。

有了这个性质，我们就可以把这道题的平面直角坐标系转到树上，考虑树上算法解决。

现在我们考虑修改的影响，不难发现，这次修改会对包含其的最小矩形到根节点上的一根链产生影响，直接暴力改这根链，肯定是超时的。这里树链剖分当然可以解决，但是我们可以通过树上差分更简单的完成，然后就类似[Vani有约会] 雨天的尾巴一样 dfs 一遍线段树合并上去即可。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

可并堆

例题

P3261 [JLOI2015] 城池攻占

P3273 [SCOI2011] 棘手的操作

首先，找一个节点所在堆的堆顶要用并查集，而不能暴力向上跳。

再考虑单点查询，若用普通的方法打标记，就得查询点到根路径上的标记之和，最坏情况下可以达到 \(\mathcal O(n)\) 的复杂度。如果只有堆顶有标记，就可以 \(\mathcal O(\log n)\)（只有路径压缩的并查集复杂度）地查询了，但如何做到呢？

可以用类似启发式合并的方式，每次合并的时候把较小的那个堆标记暴力下传到每个节点，然后把较大的堆的标记作为合并后的堆的标记。由于合并后有另一个堆的标记，所以较小的堆下传标记时要下传其标记减去另一个堆的标记。由于每个节点每被合并一次所在堆的大小至少乘二，所以每个节点最多被下放 \(\mathcal O(\log n)\) 次标记，暴力下放标记的总复杂度就是 \(\mathcal O(n \log n)\)。

再考虑单点加，先删除，再更新，最后插入即可。

然后是全局最大值，可以用一个平衡树/左偏树/multiset 来维护每个堆的堆顶。

所以，每个操作分别如下：

1. 暴力下传点数较小的堆的标记，合并两个堆，更新 size、tag，在 multiset 中删去合并后不在堆顶的那个原堆顶。
2. 删除节点，更新值，插入回来，更新 multiset。需要分删除节点是否为根来讨论一下。
3. 堆顶打标记，更新 multiset。
4. 打全局标记。
5. 查询值+堆顶标记+全局标记。
6. 查询根的值+堆顶标记+全局标记。
7. 查询 multiset 最大值+全局标记。

总结：实际上本题唯一难点就是单点查询，普通合并的话我们就需要查点到根路径上的标记和，因为左偏树深度没有保证，所以我们只能查堆顶的标记，而我们结合启发式合并，每次都将子树大小较小的那个堆的标记暴力更改至子树大小较大的那个堆的标记，中间的变化量就需要暴力进入较小的堆中一个一个的修改，每次单点查询就看堆顶的标记即可，这样复杂度就是对的。

Ds 杂题

本来不想开的，但确实有些题很奇怪。。。

P1600 [NOIP 2016 提高组] 天天爱跑步

倍增+dfn序差分好题。

P6623 [省选联考 2020 A 卷] 树

套路的，我们选择把每个点的贡献拆开计算。我们先考虑一个点，它对祖先的贡献为：

\[c,c+1,c+2,\cdots \]

我们试着挖掘它们的二进制表示。

不妨设 \(c=3\)，那么它的二进制表示就是：

\[+0\quad=\quad0111\\+1\quad=\quad0100\\+2\quad=\quad0101\\+3\quad=\quad0110\\+4\quad=\quad0111\\+5\quad=\quad1000\\+6\quad=\quad1001\\+7\quad=\quad1010\\+8\quad=\quad1011\\+9\quad=\quad1100\\ \cdots\quad\cdots \quad\cdots \]

我们找第一位（以 \(0\) 为基准）进行观察：

\[+0\quad=\quad01\textcolor{red}11\\+1\quad=\quad01\textcolor{red}00\\+2\quad=\quad01\textcolor{red}01\\+3\quad=\quad01\textcolor{red}10\\+4\quad=\quad01\textcolor{red}11\\+5\quad=\quad10\textcolor{red}00\\+6\quad=\quad10\textcolor{red}01\\+7\quad=\quad10\textcolor{red}10\\+8\quad=\quad10\textcolor{red}11\\+9\quad=\quad11\textcolor{red}00\\ \cdots\quad\cdots \quad\cdots \]

发现它是：\(1001100110\cdots\)，循环节为 \(0011\)。同理从低往高第 \(k\) 位，它的循环节长度就是 \(2^{k+1}\)，是 \(\underbrace{00\cdots 0}_{2^k个0}\underbrace{11\cdots 1}_{2^k个1}\)。

我们考虑对于每一位分别计算贡献。那么，根据题面，对于每一位，它对它的 \(0,1,2,⋯\) 级祖先的贡献，就依次是上面表格中的那一列的值。

而我们要求的是每一个点的异或和，所以说其实对于第 \(k\) 位，就是相当于把它的第

\[[0\times 2^{k+1}+a,0\times 2^{k+1}+a+2^k )\cup \\ [1\times 2^{k+1}+a,1\times 2^{k+1}+a+2^k )\cup\\ [2\times 2^{k+1}+a,2\times 2^{k+1}+a+2^k )\cup\\ \cdots \]

但是，观察到，所有要异或 \(2^k\) 的差分数组，它们的下标 \(\mod 2^k\) 都一样，这就意味着，我们可以开一个新的差分数组，\(s_{k,i}\)，它等于所有当前dfs到的，深度 \(d\mod 2^k=i\) 的所有的点的差分数组。

那么，我们发现，我们修改的那很多的差分，就是单独地改了一个 \(s_{k,a}\)，这样就是 \(\mathcal O(1)\) 的了

但是怎么找到一个点的差分值呢？我们发现，它的差分值，就等于进入这个点的子树前的 \(s_{k,d}\) （\(d\)为该点深度） 与出该点子树后的 \(s_{k,d}\) 的异或差（其实就是异或和）

因为我们一个点的差分，就是其子树内的点对于 \(s_{k,d}\) 的修改，而这样做差刚好就只算了子树内贡献，所以是对的。

所以，我们对于每一个节点的每一位，都可以 \(\mathcal O(1)\) 地计算贡献和差分数组，所以总复杂度 \(\mathcal O( n\log n)\)。

P9067 [Ynoi Easy Round 2022] 虚空处刑 TEST_105

好题。

注意到颜色种类数不增，也就是说合法合并次数最多为 \(\mathcal O(n)\) 次。

现在问题转化为快速找到与 \(x\) 所在连通块相邻的 \(y\) 颜色连通块。

考虑维护 map<int,list<int> >mp C[N]，\(C_{i,j}\) 表示与 \(i\) 点所在连通块相邻的 \(j\) 色连通块序列。那么当 \(a_i \leftarrow y\) 时，直接对 \(C_x\) 和 \(C_i|i \in C_{x,y}\) 进行启发式合并，然后发现 \(\forall v\) 与 \(x\) 相邻，我们要更新 \(C_{v,y}\)，假了。但是我们发现，如果我们只考虑父亲的 \(C_{fa_i,y}\) 的更改，那么复杂度就是对的，那么其它的 \(v\) 都是在连通块的下方，我们可以这样优化——对于每个连通块只维护在它下方的连通块，在它上方的只有一个也就是它的父亲，我们可以直接更改父亲的 \(C_{fa_i,y}\)，而其它点的 \(C_{v,y}\) 就不用更新，因为根据刚才的加粗文字，我们对于一个点 \(x\) 只记录了它下方的连通块，所以 \(i\) 更改的时候，我们就不需更改其余 \(C_{v,y}\) 了。

（以上不懂你也可以当作幻觉）那么我们只需根据【Tricks】里记载——邻域信息不维护父亲（因为父亲可以单独处理）以及“lxl 说过，这种邻域信息维护父亲一定死”。综上，所以设 \(C_{i,j}\) 表示 \(i\) 点所在连通块下方的 \(j\) 色连通块序列（注意这里序列记录的是 \(j\) 色连通块中深度最小的那个点的编号）。那么当 \(a_x\leftarrow y\) 时，直接对 \(C_x\) 和 \(C_i|i \in C_{x,y}\) 进行启发式合并，然后我们只需更新 \(C_{fa_x,y}\) 了。

这里我们没必要从 \(C_{fa_x,a_x}\) 里面删掉 \(x\)，启发式合并特判一下就行。

对于 list 的拼接，可以使用 splice 函数，少一些码量。

时间复杂度：\(\mathcal O(n \log^2 n)\)。

8165 -- 【9.26CSP-S模拟】排队

好题值得经常复习。

我们发现最后的序列一定是一段一段的颜色段。

那么我们可以先预处理出每个点最后会处于哪个颜色段中，然后最后再来确定这个点在它所在的颜色段中的具体位置。两者都可通过二分解决。第二种情况我们需要倒着遍历每个颜色段中插入的点。

时间复杂度：\(\mathcal O(n\log^2 n)\)。

注意实现细节。