坐标系的平移与旋转变化
一、坐标系的平移变化
定义
坐标原点发生变化,而坐标轴的方向不发生改变,这样的变化成为坐标系的平移变化。
分析
记平移后的坐标原点为 \(O'(h, k)\), 取坐标系上任一点 \(P(x, y)\), 利用平面向量,有
\[\vec{OP} = \vec{OO'} + \vec{O'P}
\]
即
\[(x, y) = (h, k) + (x', y')
\]
因此,得到平移后的坐标与原坐标的关系式如下
\[\begin{cases}
x = x' + h \\ y = y' + k
\end{cases}
\text{ (1) 或 }
\begin{cases}
x' = x - h \\ y' = y - k
\end{cases}
\text{ (2)}
\]
我们称 (1) 式和 (2) 式为平移公式。
示例
问题
将坐标原点 \(O\) 点平移至 \(O'(2, -3)\), 求以下各项在新坐标系中的方程。
- 点 \(A(4, 6)\);
- 直线 \(x + 3y = 2\);
- 曲线 \(9 x^2 + 4 y^2 - 36x + 24y - 36 = 0\).
解答
根据平移公式,平移前后的坐标有以下关系
\[\begin{cases}
x = x' + 2 \\ y = y' - 3
\end{cases}
\text{ (1) 或 }
\begin{cases}
x' = x - 2 \\ y' = y + 3
\end{cases}
\text{ (2)}
\]
-
由(2)式,得
\[\begin{cases} x' = x - 2 = 2 \\ y' = y + 3 = 9 \end{cases} \]故平移后的坐标为 \(A(2, 9)\)
-
由(1)式,得
\[ (x' + 2) + 3 (y' - 3) = 2 \]整理得,平移后的直线方程为
\[ x + 3y = 9 \] -
由(1)式, 得
\[ 9(x' + 2)^2 + 4(y' - 3)^2 - 36x' + 24y' -36 = 0 \]整理得, 平移后的曲线方程为
\[ 9 x^2 + 4 y^2 - 36 = 0 \]即
\[ \dfrac{x^2}{4} + \dfrac{y^2}{9} = 1 \]可知,该曲线为对称中心在 O'(2, -3) 的椭圆
二、坐标系的旋转变化
定义
保持原点及坐标轴的夹角不变,将两坐标轴绕原点(逆时针)旋转同一角度的变化,称为坐标系的旋转变化。
分析
将坐标系 \(Oxy\) 逆时针旋转 θ 得到新坐标系 \(Ox'y'\), 则 \(x'\), \(y'\) 正半轴上的单位向量为
\[\vec{e_1} = (\cos θ, \sin θ)
\]
\[\vec{e_2} = (-\sin θ, \cos θ)
\]
则点 \(P(x, y)\) 在新坐标系的坐标即为 \(\vec{OP}\) 在两个单位向量上的投影
\[ x' = \vec{OP} \cdot \vec{e_1} = x \cos θ + y \sin θ
\]
\[ y' = \vec{OP} \cdot \vec{e_2} = -x \sin θ + y \cos θ
\]
因此我们可以得到旋转公式
\[\begin{cases}
x = x' \cos θ - y' \sin θ \\ y = x' \sin θ + y \cos θ
\end{cases}
\text{ (1) 或 }
\begin{cases}
x' = x \cos θ + y \sin θ \\ y' = -x \sin θ + y \cos θ
\end{cases}
\text{ (2)}
\]
示例
问题
将坐标系 \(Oxy\) 旋转 45°, 求以下各项在新坐标系中的方程。
- 点 \(B(6, -1)\);
- 直线 \(x + 3y = 2\);
- 曲线 \(x^2 + y^2 - 6xy + 4= 0\).
解答
根据旋转公式,旋转前后的坐标有以下关系
\[\begin{cases}
x = \dfrac{\sqrt{2}}{2} x' - \dfrac{\sqrt{2}}{2} y' \\
y = \dfrac{\sqrt{2}}{2} x' + \dfrac{\sqrt{2}}{2} y'
\end{cases}
\text{ (1) 或 }
\begin{cases}
x' = \dfrac{\sqrt{2}}{2} x + \dfrac{\sqrt{2}}{2} y \\
y' = -\dfrac{\sqrt{2}}{2} x + \dfrac{\sqrt{2}}{2} y
\end{cases}
\text{ (2)}
\]
-
由(2)式,得
\[\begin{cases} x' = \dfrac{\sqrt{2}}{2} x + \dfrac{\sqrt{2}}{2} y = \dfrac{5 \sqrt{2}}{2} \\ y' = -\dfrac{\sqrt{2}}{2} x + \dfrac{\sqrt{2}}{2} y = -\dfrac{7 \sqrt{2}}{2} \end{cases} \]故旋转后的坐标为 \(A(\dfrac{5 \sqrt{2}}{2}, -\dfrac{7 \sqrt{2}}{2})\)
-
由(1)式,得
\[ (\dfrac{\sqrt{2}}{2} x' - \dfrac{\sqrt{2}}{2} y') + 3 (\dfrac{\sqrt{2}}{2} x' + \dfrac{\sqrt{2}}{2} y') = 2 \]整理得,旋转后的直线方程为
\[ 2x + y = \sqrt{2} \] -
由(1)式, 得
\[ (\dfrac{\sqrt{2}}{2} x' - \dfrac{\sqrt{2}}{2} y')^2 + (\dfrac{\sqrt{2}}{2} x' + \dfrac{\sqrt{2}}{2} y')^2 - 6(\dfrac{\sqrt{2}}{2} x' - \dfrac{\sqrt{2}}{2} y') (\dfrac{\sqrt{2}}{2} x' + \dfrac{\sqrt{2}}{2} y') + 4= 0 \]整理得, 旋转后的曲线方程为
\[ x^2 - 2 y^2 - 2 = 0 \]即
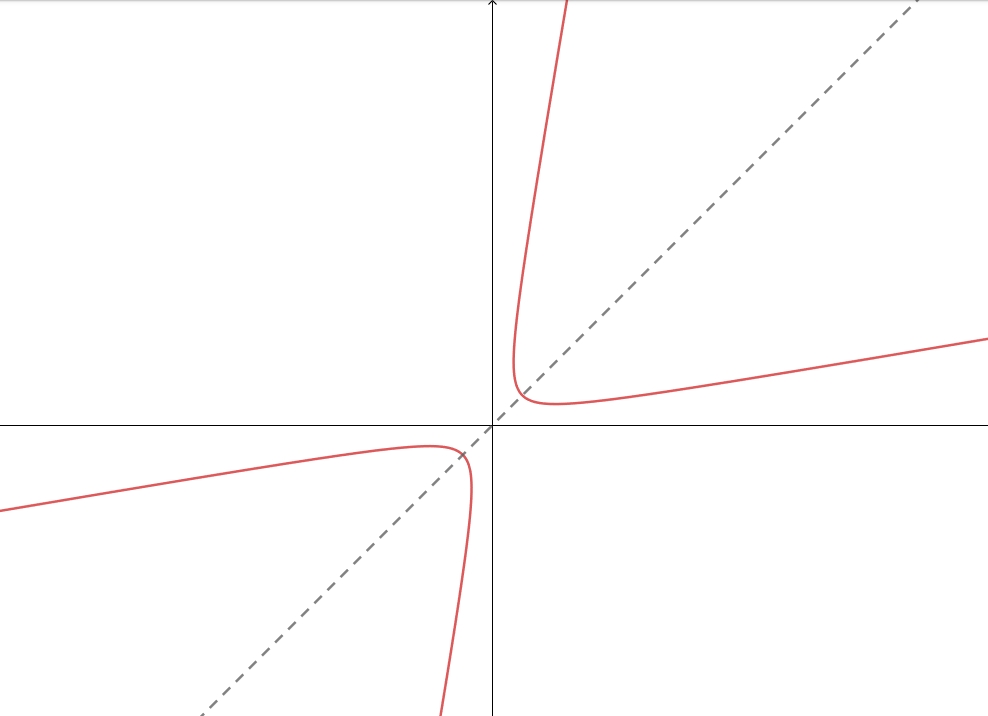
\[ \dfrac{x^2}{2} - y^2 = 1 \]可知,该曲线为对称轴为直线 \(y = x\) 的双曲线


 浙公网安备 33010602011771号
浙公网安备 33010602011771号