高精度加法&乘法

高精度加法&乘法

做题时常常遇到数值异常庞大的高精度题型，即使long long也无法存储，这时我们只能用模拟的方式，将数据存储在string中。

高进度加法：

• 步骤：

  • 首先搞定输入：

  • 由于是加法，所以输入的数据应该非常巨大，所以我们应该用string来存储：

  • string s1,s2;
    int a[100001],b[100001],c[100001];	
    //a,b作为两个待加数，c作为结果
    int main()
    {
        cin >> s1 >> s2;	//用来存储输入的数据
    }
    

  • 小技巧：利用数组的第一项来记录数组的长度，这样可以省出两个变量，但是记得在调用的时候for要从1开始。

    a[0] = s1.size(); b[0] = s2.size();
    

  • 之后我们来将输入的数据(string)转换成真实的数字数据：

    for(int i = 1; i <= a[0]; i++)
        a[i] = s1[a[0]-i] - "0";
    for(int i = 1; i <= b[0]; i++)
        b[i] = s2[b[0]-i] - "0"
    

    具体的实现机理为：

    对于当前的位，用当前字符的ASCII值减去0的ASCII的值实现真实的数字值，再强行转换成int类型，将值赋给a,b两个数组中，完整的处理数据。

  • 转换好数据，我们接着实行加法运算：

    int len = max(a[0],b[0]);
    for(int i = 1; i <= len; i++) {		//记得用0作为数组的长度
    		c[i] = a[i]+b[i];		//对位加对位，不用担心其中的一个数组的长度，已经初始化为0
    }
    

  • 数据存好了，但是可以想到，有的位大于十，于是接着我们来实现进位操作：

    for(int i = 1; i <= len; i++) {
        c[i] = a[i]+b[i];
        if(c[i] > 9) {
            c[i+1] += c[i]/10;
            c[i] %= 10;
        }
    }
    

  • 这时候我们可以想到，c 数组中仍然有未存储的数据，其当前为0，所以我们肯定不能弃之不管。因此我们可以有如下操作：

    while(c[len] == 0 && len > 1)
        len--;
    //也可以写成：
    for(len; len > 1 && c[len] == 0; len--);
    

  • 最后的最后：输出

    for(int i = len; i >= 1; i--) {
        cout << c[i];
    }
    

• 以下为完整代码：

  #include <bits/stdc++.h>
  using namespace std;
  string s1,s2;
  int a[10000001],b[10000001],c[10000001];
  int len;
  
  int main()
  {
      cin >> s1 >> s2;
      //搞定输入，存储数据
      a[0] = s1.size(); b[0] = s2.size();
      for(int i = 1; i <= a[0]; i++)
          a[i] = s1[a[0]-i] - '0';
      for(int i = 1; i <= b[0]; i++)
          b[i] = s2[b[0]-i] - '0';    //首先利用字符串相减的性质，将0的ASCII和当前数字相减
          //所得到的为数字的真实数值，之后强制转换成int，得到答案。
  
      len = max(a[0],b[0]);
      for(int i = 1; i <= len; i++) {
      	c[i] = a[i]+b[i];
          if(c[i] > 9) {
              c[i+1] += c[i]/10;      //注意次序!
              c[i] %= 10;
          }
      }
  
      while(c[len] == 0 && len > 1)
          len--;
  
      for(int i = len; i >= 1; i--)
          cout << c[i];
      return 0;
  }
  

高精度乘法

• 步骤：

  • 与加法类似，首先搞定输入：

    • 同样是采用字符串转换成int进行存储：

      cin >> s1 >> s2;
      
      a[0] = s1.size(); b[0] = s2.size();
      for(int i = 1; i <= a[0]; i++)
              a[i] = s1[a[0]-i] - '0';
          for(int i = 1; i <= b[0]; i++)
              b[i] = s2[b[0]-i] - '0'; 
      

    • 之后我们进行乘法运算：

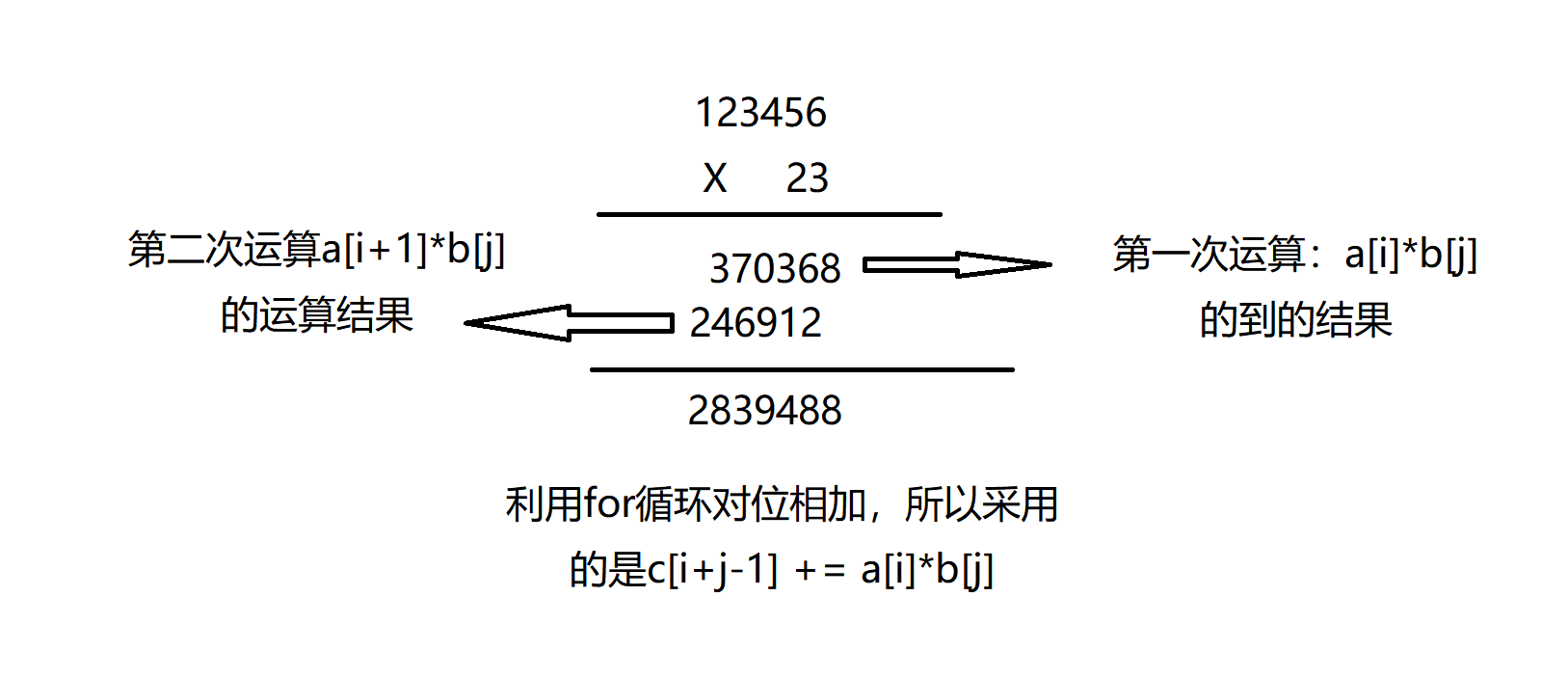
      for(int i = 1; i <= a[0]; i++) {
          for(int j = 1; j <= b[0]; j++) {
              c[i+j-1] += a[i]*b[j];
          }
      }
      

      这里要注意：由于乘法的特性，我们需要将一位和另一数组的所有位相乘，所以显然两个for是最佳选择。两个for的限制条件均为对应该数组的长度

    • 

    • 之后我们对计算好了的c数组进行进位操作：

      len = a[0]+b[0];
      for(int i = 1; i <= len; i++) {
          if(c[i] > 9) {
              c[i+1] += c[i]/10;
              c[i] %= 10;
          }
      }
      

      考虑一下，进位该进多少位？

      应该进a[0] + b[0]位，例如两个最大二位数99*99=9801(4位)

    • 之后进行清零操作：

      while(c[len] == 0 && len > 1)
          len--;
      

    • 然后输出：

      for(int i = 1; i <= len; i++) {
          cout << c[i];
      }
      

• 完整代码：

  #include <bits/stdc++.h>
  using namespace std;
  string s1,s2;
  int a[10000001],b[10000001],c[10000001];
  int len;
  
  int main()
  {
      cin >> s1 >> s2;
      //搞定输入，存储数据
      a[0] = s1.size(); b[0] = s2.size();
      for(int i = 1; i <= a[0]; i++)
          a[i] = s1[a[0]-i] - '0';
      for(int i = 1; i <= b[0]; i++)
          b[i] = s2[b[0]-i] - '0';    //首先利用字符串相减的性质，将0的ASCII和当前数字相减
          //所得到的为数字的真实数值，之后强制转换成int，得到答案。
  
      for(int i = 1; i <= a[0]; i++) {    //存储数据
          for(int j = 1; j <= b[0]; j++) {
              c[i+j-1] += a[i]*b[j];
          }
      }
      len = a[0]+b[0];    //两个n位数相乘 乘积最多是n+n位
      for(int i = 1; i <= len; i++) {     //进位
          if(c[i] > 9) {
              c[i+1] += c[i]/10;      //注意次序!
              c[i] %= 10;
          }
      }
  
      while(c[len] == 0 && len > 1)
          len--;
  
      for(int i = len; i >= 1; i--)
          cout << c[i];
      return 0;
  }