UPD 2021.7.5: 感谢 Tiw_Air_OAO 大佬提醒,钩长公式有利用 LGV 引理的神奇证法,在 2019 年集训队论文里有提到。不过菜鸡博主还没看懂/kk,以后如果有机会弄明白的话会来更新一下。
大鸽子更博辣!
最近听说了这个神奇的公式,随手百度了一下竟然几乎找不到任何有证明的博客!!于是去翻论文找到了证明,在这里搬运一下qwq
本文中所有图均源自维基百科。
本文的主角是一种非常神奇的组合结构——杨表(Young Tableau)。
杨表是一个如下图所示的结构,每一行有公共的左边界,每一列有公共的上边界,而每行的长度自上到下非严格递减,每列的长度自左到右非严格递减。

杨表在各种各样的组合模型中随处可见,例如杨表与整数拆分的方案一一对应。杨表的一大神奇之处在于,它可以用各种各样的方式构造(上下左右加一行),还能进行翻转等变换,由此可以导出整数拆分的多种 DP 方式。
而本文讨论的是杨表的拓扑序计数问题:对于一个总共有 \(n\) 个格子的杨表,给每个格子一个 \(1\) 到 \(n\) 之间的编号,使得所有格子的编号互不相同,且对于任何一对相邻格子,上面格子的编号小于下面,左面格子的编号小于右面,一共有多少种方案?
这个问题有一个异常优美的公式,不过在这之前让我们先作出一些必要的定义。
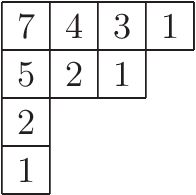
对于杨表中的每一个单元格,我们定义“钩长” (hook length) 为它本身、正下方、正右方的格子总个数。
例如在下图中,每个格子上标出了该格子的钩长。
于是重点来了:
钩长公式 (Hook Length Formula): 设杨表总共格子数是 \(n\),第 \(i\) 行第 \(j\) 列的钩长为 \(h_{i,j}\),则拓扑序个数为 \(\frac{n!}{\prod_{i,j} h_{i,j}}\),即 \(n!\) 除以每个钩长的乘积。
网上很多类似于“每个点是它和它正下方正右方的最小值的概率是 \(\frac{1}{h_{i,j}}\),相乘就是答案”的论述,显然都是伪证。接下来让我们有理有据地证明这个结论。
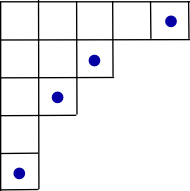
这个证明基于一个递推的想法——设一张杨表 \(A\) 的拓扑序个数为 \(T\),该公式给出的答案为 \(H\). 对于较小的情况,容易验证 \(T\) 和 \(H\) 是相等的;可以发现 \(T\) 之间具有一个显然的递推关系:枚举这张杨表中的所有角落方格,将该方格去掉之后得到的杨表的 \(T\) 值求和,就是当前这张杨表的 \(T\) 值。在这里,角落方格是指所有能被标号为 \(n\) 的方格,即钩长为 \(1\) 的方格。如下图所示,角落方格被标了蓝点。
那么,我们只需要证明 \(H\) 也具有相同的递推关系,就可以证明对于任意杨表都有 \(T=H\). 对此,数学家们构造性地给出了一个转化,称为The Hook Walk:
(1) 首先从 \(n\) 个格子中随机选择一个作为起点,开始游走。
(2) 如果当前在角落格子,那么游走结束;否则,从该格正右方和正下方的 \(\frac{1}{h_{i,j}-1}\) 个格子中等概率随机选择一个,跳到所选的点,继续该步骤。
假设在角落格 \((a,b)\) 结束的概率是 \(p_{a,b}\),那么可以断言
即在角落 \((a,b)\) 结束的概率等于 \((a,b)\) 标号为 \(n\) 的拓扑序在所有拓扑序中所占的比例。
为什么呢?考虑随机游走的过程。下证一个引理:固定起点 \((c,d)\)、终点 \((a,b)\) 以及路径经过的所有行的序列 \(S_1[1..m_1]\)、所有列的序列 \(S_2[1..m_2]\). 考虑所有满足这一条件的路径,其概率总和为 \(f(a,b,c,d,S_1,S_2)=\prod_{i\in S_1}\frac{1}{h_{i,b}-1}\cdot \prod_{j\in S_2}\frac{1}{h_{a,j}-1}\).
上面的等式右边那个乘积我们称作 \(P\). 可以得到 \(f\) 的递推关系:考虑第一步的走法,有
我们对路径的长度使用数学归纳法,那么根据归纳假设有
即 \(f(a,b,c,d,S_1,S_2)=\frac{1}{h_{c,d}-1}(h_{c,b}-1+h_{a,d}-1)\cdot P\)
画一画图可以发现 \(h_{c,b}+h_{a,d}=h_{c,d}+1\),于是 \(f(a,b,c,d,S_1,S_2)=P\).
那么考虑在固定 \(a,b\) 的情况下,对所有可能的 \(a,b,S_1,S_2\) 求和再除以起点的选择数 \(n\),结果就是
即为终止在 \((a,b)\) 的概率,简单计算得知它恰好等于 \(\frac{H(A-(a,b))}{H(A)}\),于是大功告成!


