红黑树
2-3-4树
JAVA技术交流群:737698533
定义
- 所有的叶子节点都拥有相同的深度
- 节点只能是2-节点,3-节点,或者4-节点
- 2节点 包含一个元素的节点,有两个子节点
- 3节点 包含两个元素的节点,有三个子节点
- 4节点 包含三个元素的节点,有四个子节点
- 所有节点都有至少两个子节点或没有子节点
来解释一下性质和一些定义
- 任意一个叶子节点(也就是没有子节点的节点)到根节点的距离一致
- 一个节点中可能包括1,2,3个元素,有2,3,4,个子节点,具体可以看下面的图
- 一个节点要么有至少两个子节点,要么没有节点
关于子节点如何定义的
- 2节点 左子树所有元素小于key1,右子树所有元素大于key1
- 3节点 左子树所有元素小于key1,中间子树所有元素大key1小于key2,右子树大于key2
- 4节点 左子树所有元素小于key1,第二个子树所有元素大于key1小于key2,第三个子树所有元素大于key2小于key3,右子树所有元素大于key3
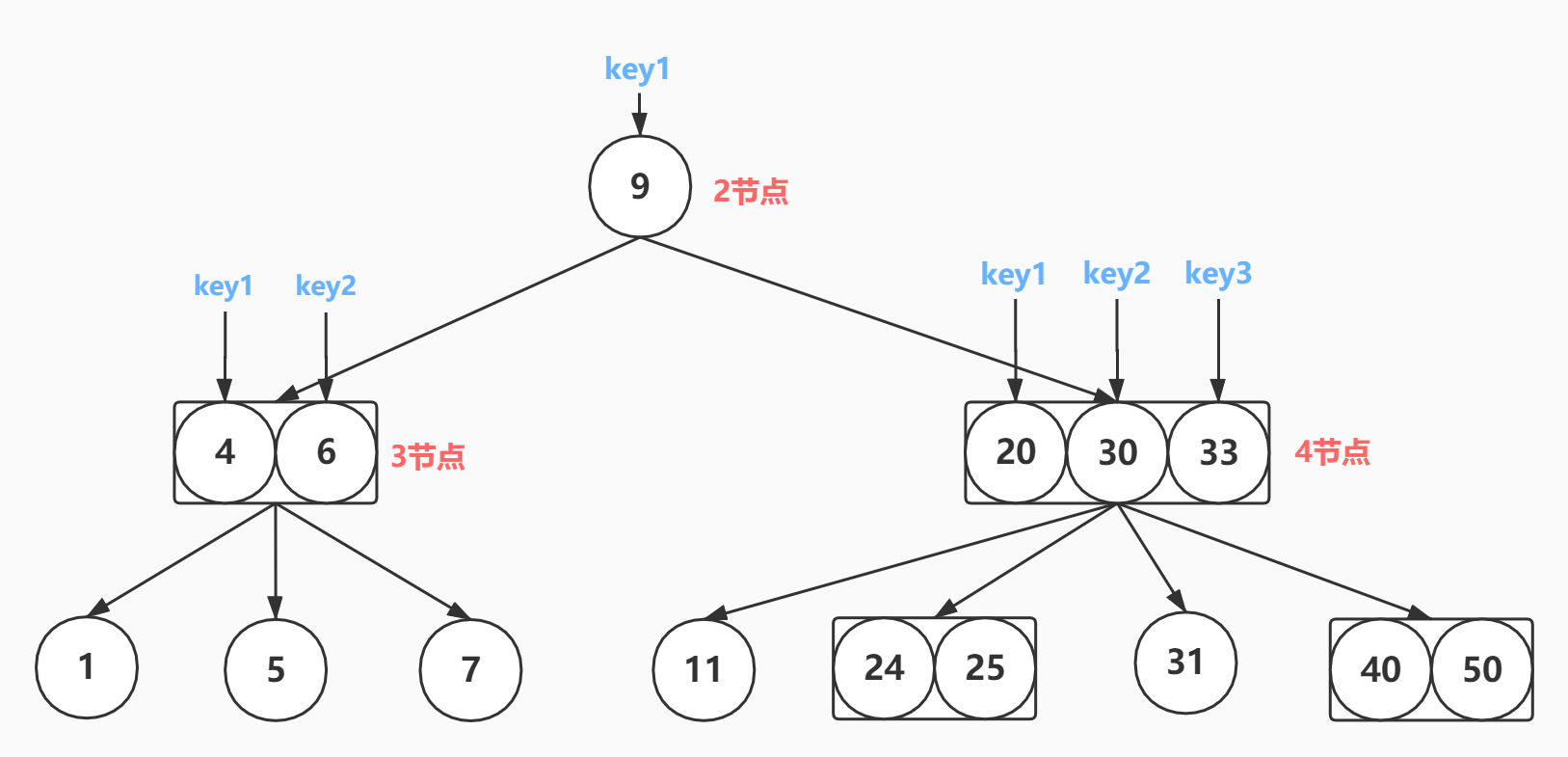
为什么要提到234树呢,因为234树和红黑树是完全等价的,在程序中实现234树比较繁琐,所以使用了红黑树来代替
来看234树的添加操作
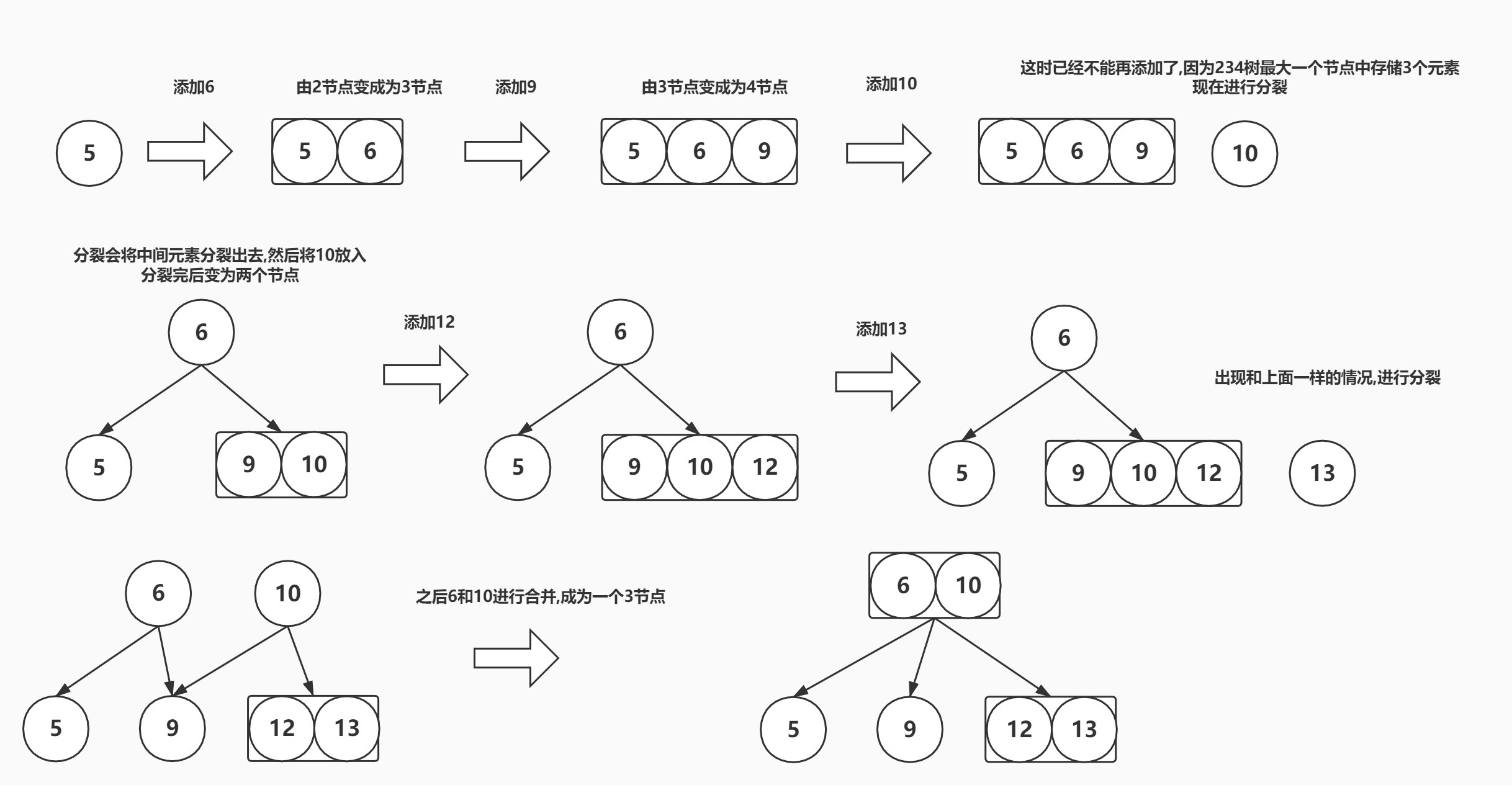
添加如果出现需要分裂的情况,分裂出的元素首先进行和父级合并,如果父级已经是4节点那么将父级分裂,递归操作
234树的生长全部都是从叶子节点进行生长的,从叶子节点进行分裂向上延伸
红黑树
性质
- 每个节点要么红色,要么黑色
- 根节点是黑色
- 每个子节点 (NIL) 是黑色
- 每个红色节点的两个子节点一定是黑色
- 任意一节点到每个叶子节点的路径都包含数量相同的黑节点
解释一下性质
性质4和性质5说一下
如果一个红色节点那么它的两个子节点必须为黑色,包括nil节点,也就是说不能有两个红色节点相连
任意一个叶子节点或没有子节点的节点到根节点经过的黑色节点数量都一致,不懂下面再解释
叶子节点 : 标记为NIL,为虚拟节点,颜色必须为黑色,234中叶子节点为没有子节点的节点,而红黑树的叶子节点是虚拟的节点
234树和红黑树对比
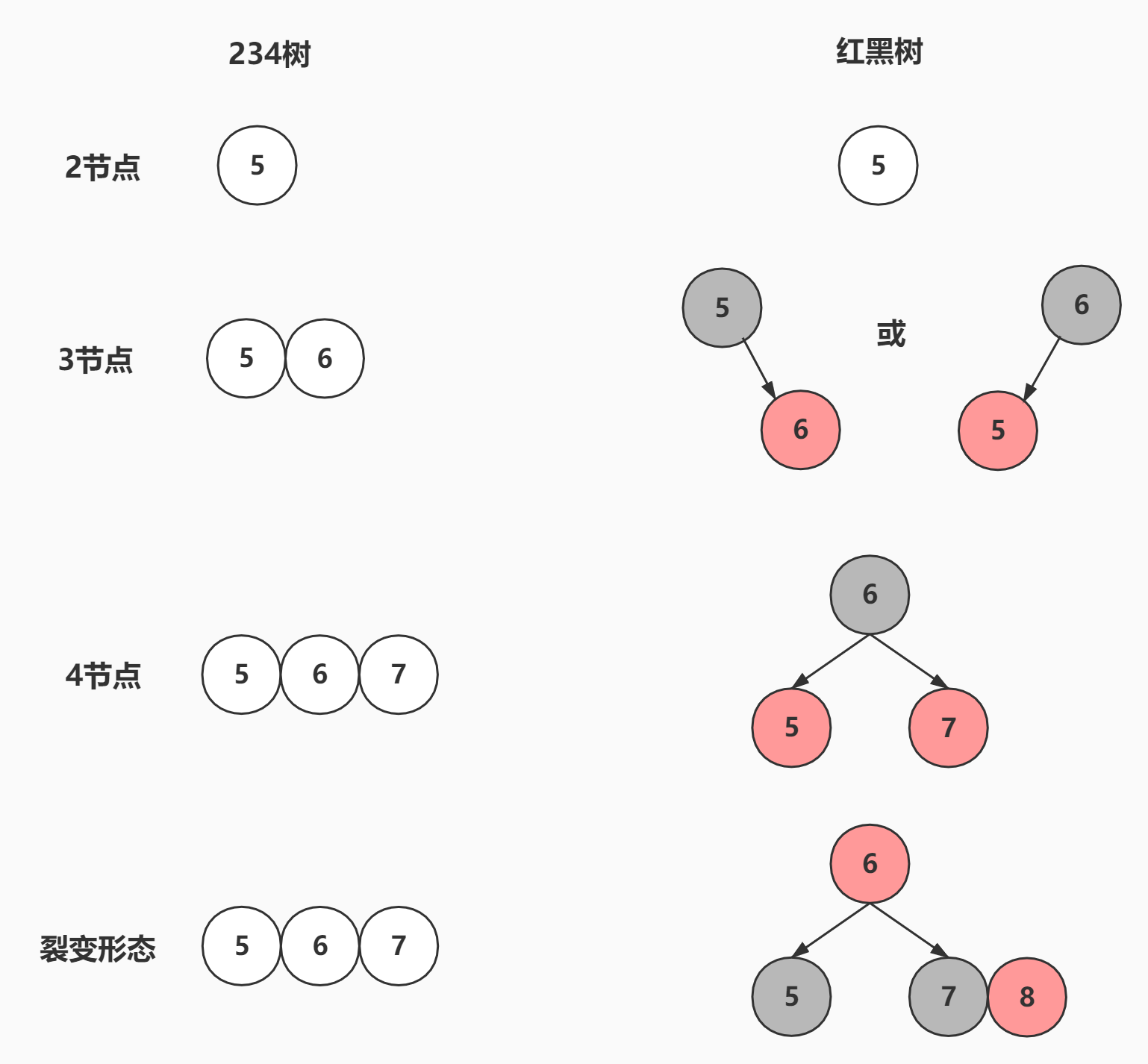
3节点的两种形态如果红色在左边就叫做左倾,红色在右边就叫做右倾
将234树进行转换为红黑树操作
右倾
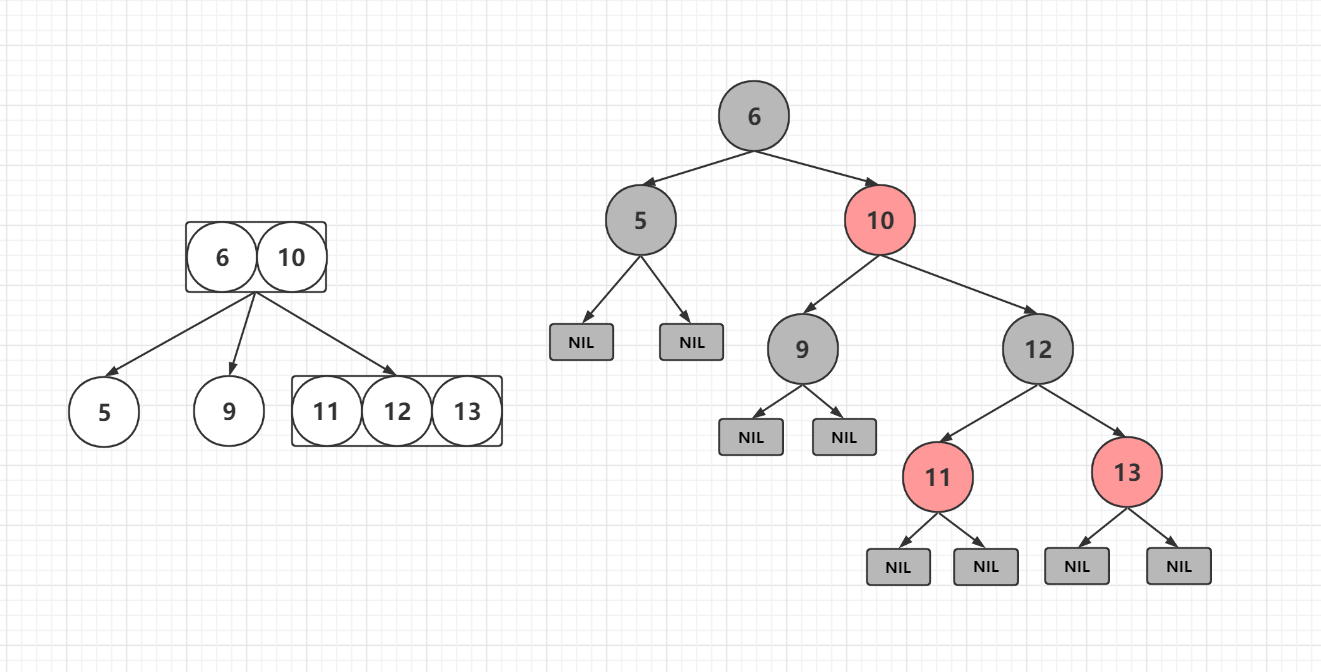
左倾
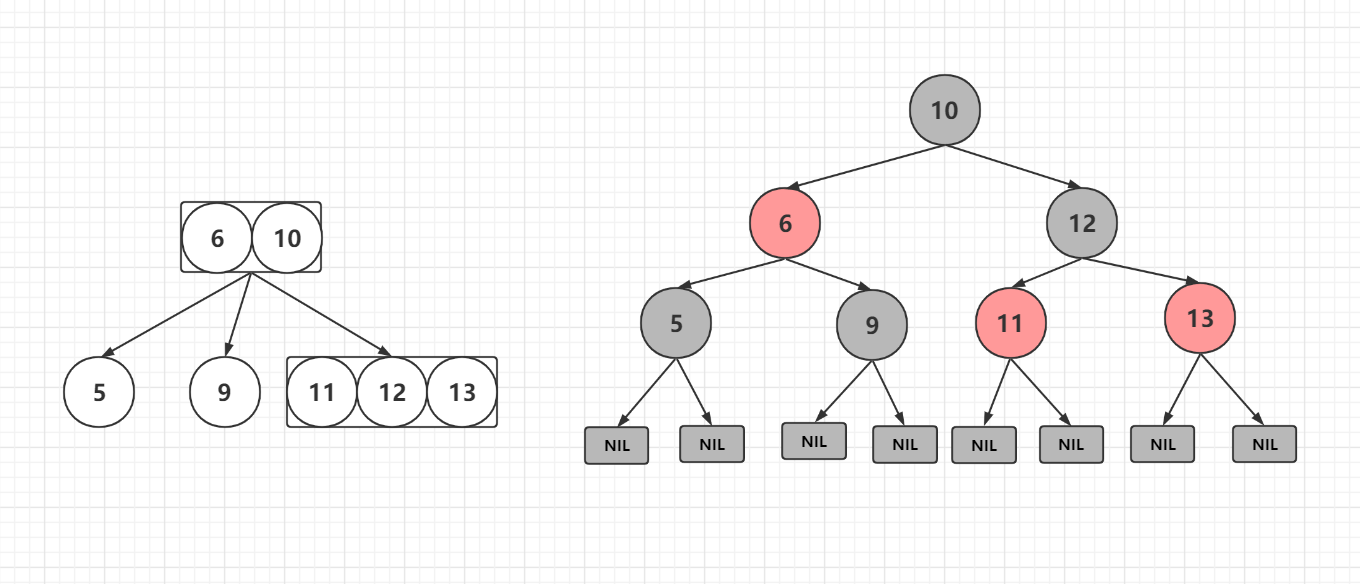
现在来看一下几个没有子节点的节点下面其实都有两个NIL节点我们可以任意从一个nil节点出发,到6根节点,所经过的黑色节点个数是一样的,一般情况下NIL节点是不画出来的,但是不代表不存在
红黑树操作
变色:节点的颜色由黑变红或者由红变黑
左旋:以某个节点作为旋转点,其右子节点变为旋转节点的父节点,右子节点的左子节点变为旋转节点的右子节点,左子节点保持不变。
右旋:以某个节点作为旋转点,其左子节点变为旋转节点的父节点,左子节点的右子节点变为旋转节点的左子节点,右子节点保持不变
看图!
右旋操作
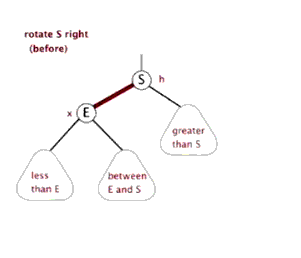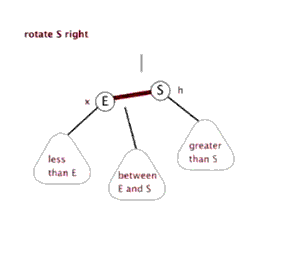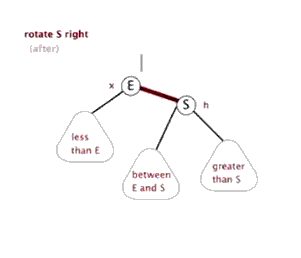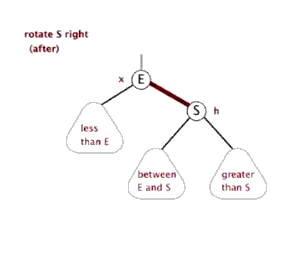
左旋操作
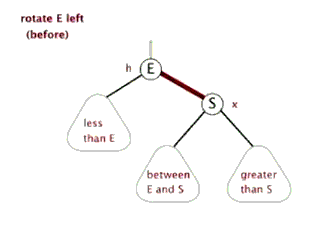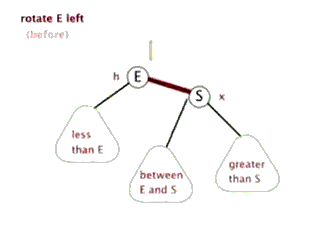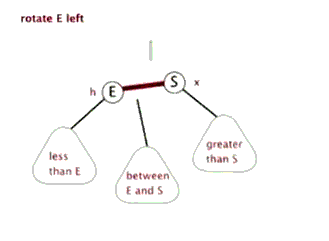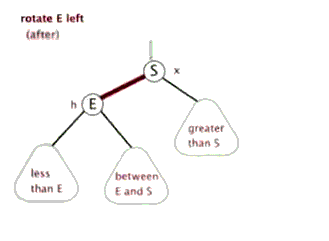
新增节点
对比234树进行添加
红黑树所有添加的节点默认都为红色
1 添加一个根节点
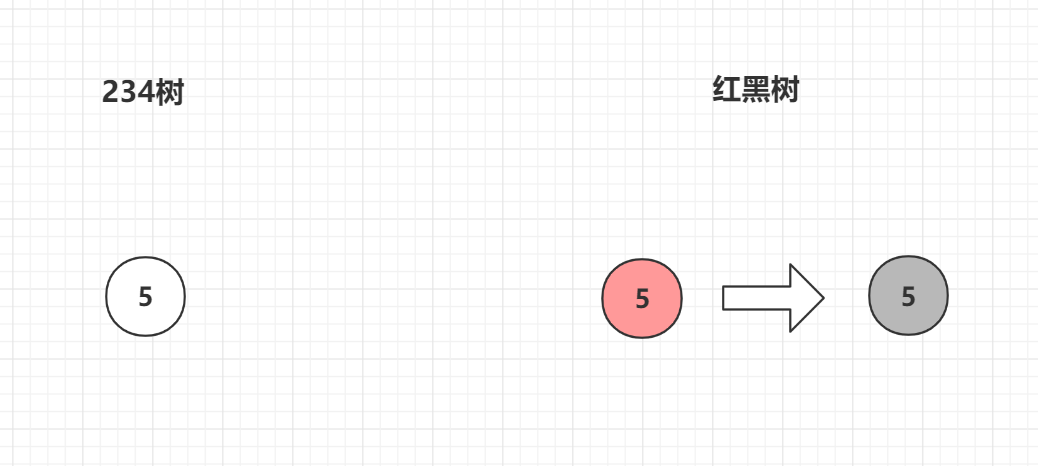
添加第一个默认为红色的节点,发现与红黑树性质"根节点必须为黑色"冲突,我们将5变色为黑色即可,完成添加操作
2 添加一个节点,与2节点合并

3 添加一个节点,与3节点合并
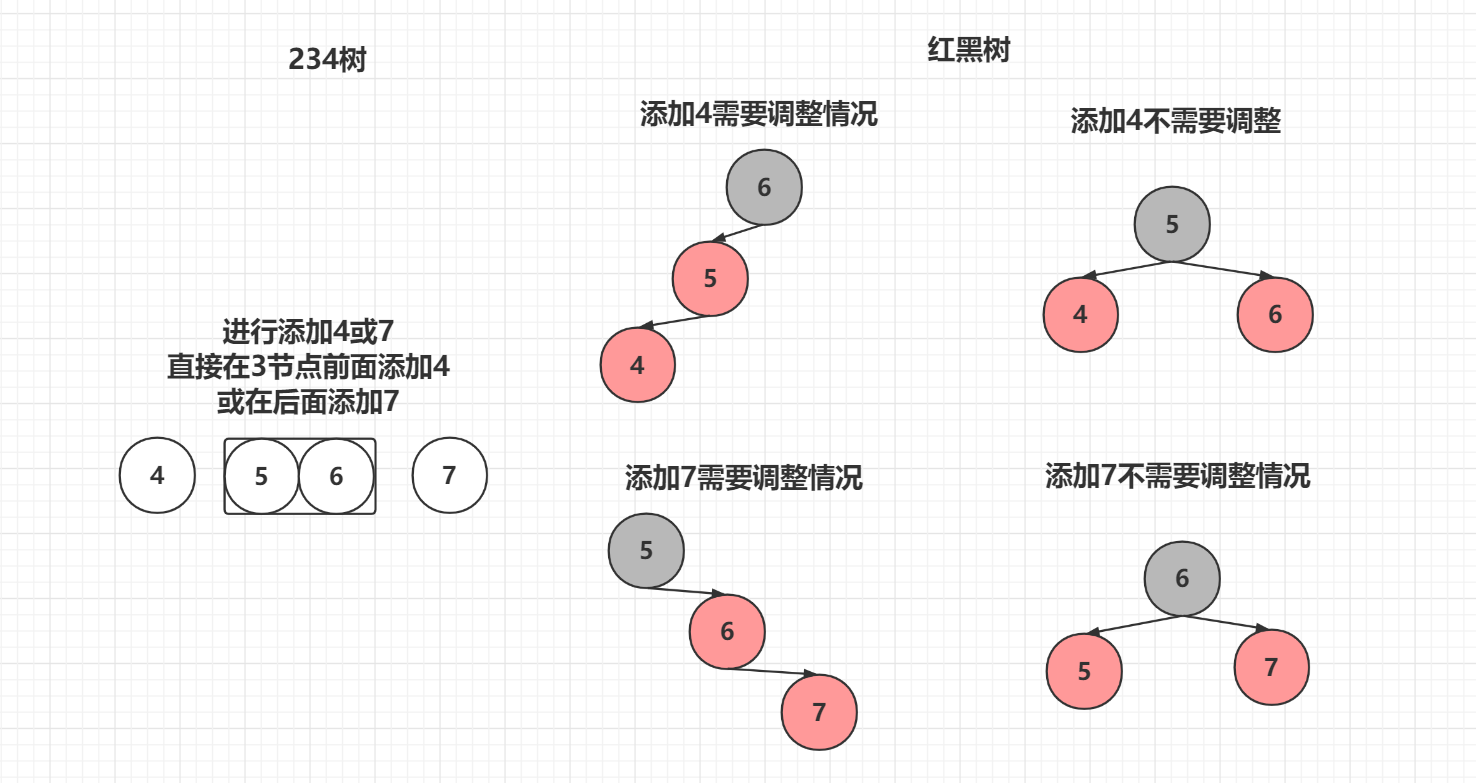
根据234树转红黑树的两种状态导致添加时可能会出现两个红色节点相连的情况
左倾通过选转和变色可以变成右倾的状态,反之亦然
4 添加一个节点和4节点合并
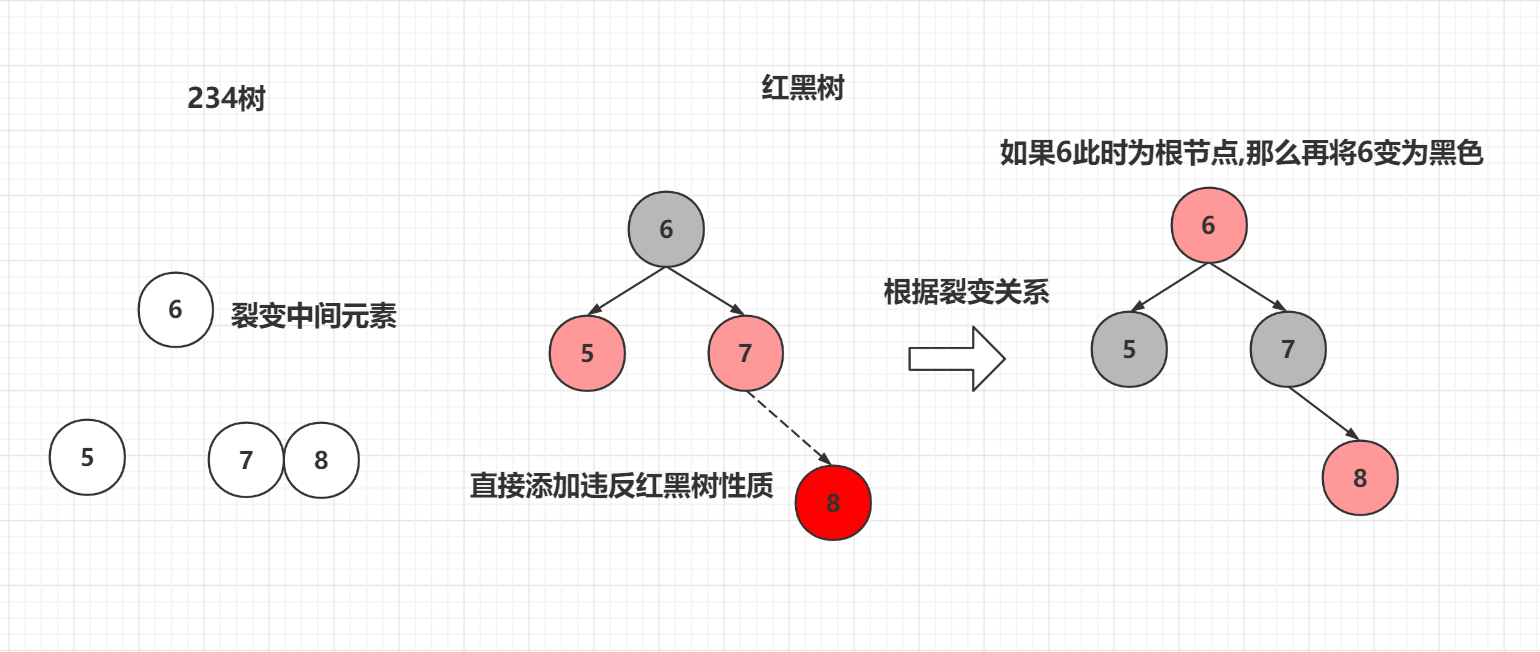
我们回到3和4,其中有需要调整的树
对于3里面的两种情况,看234树和红黑树的对比,4节点的红黑树形态是上面黑色节点左右两边各一个红色节点,而现在是三个元素一条线,上面黑色节点,下面两个红色,我们已经知道它的最终形态是什么样子,只需要进行调整即可
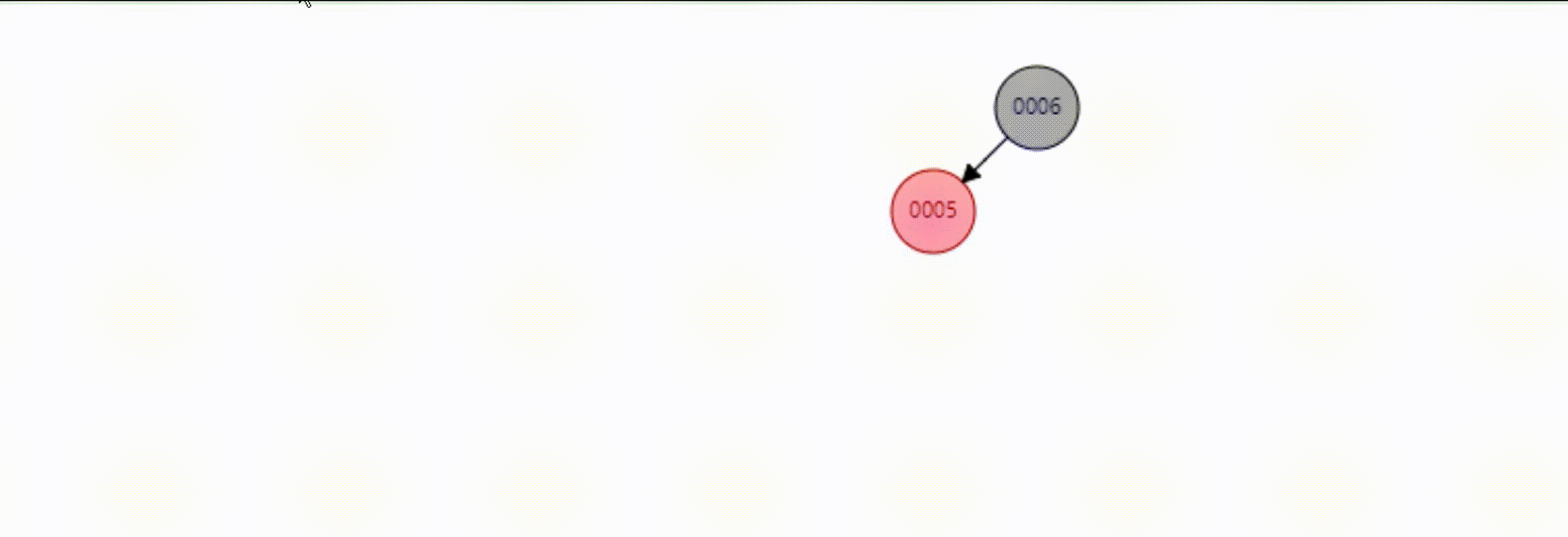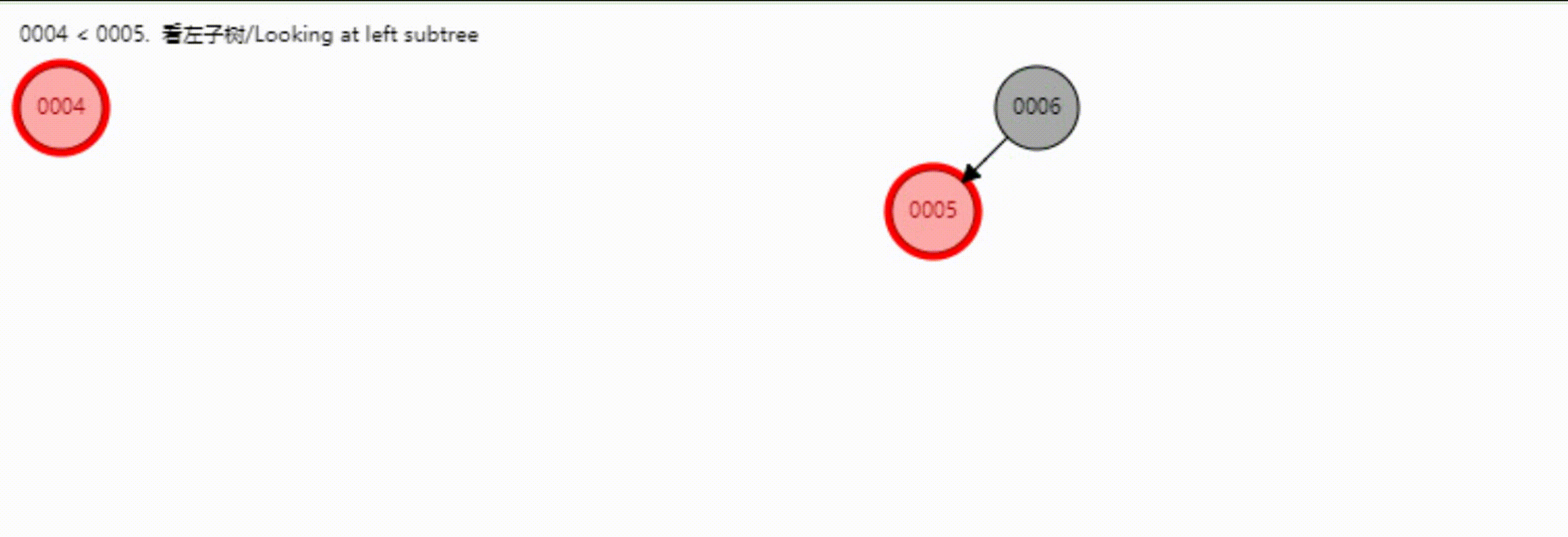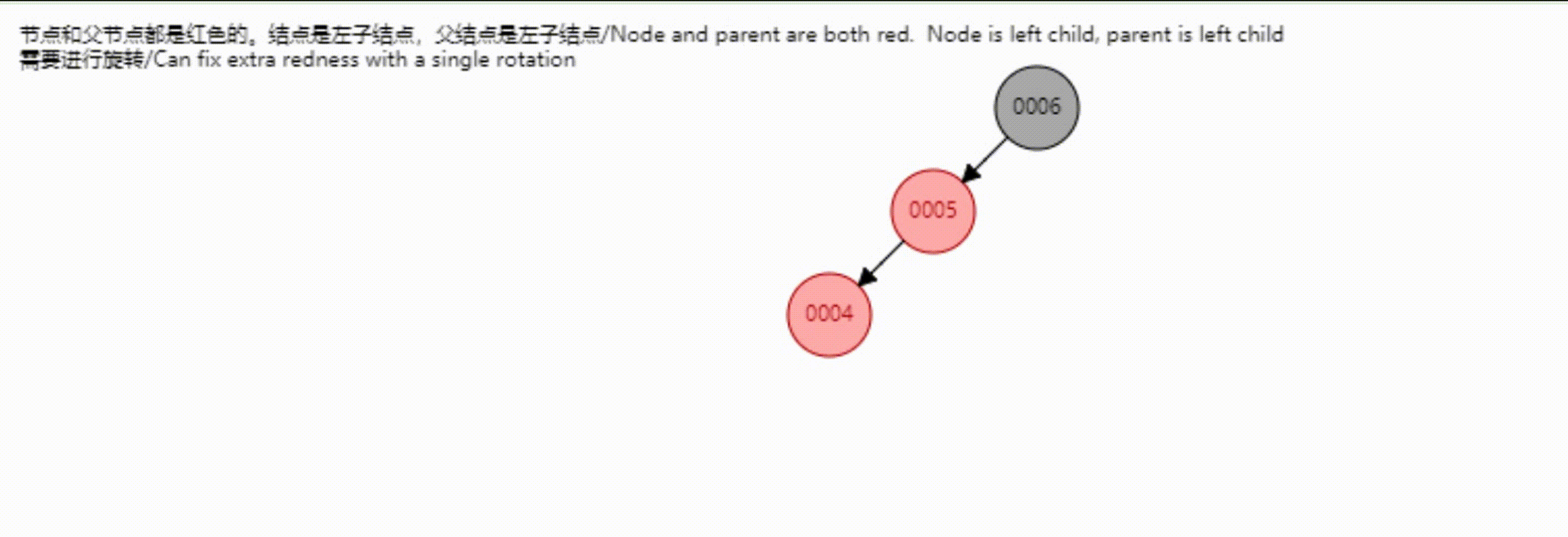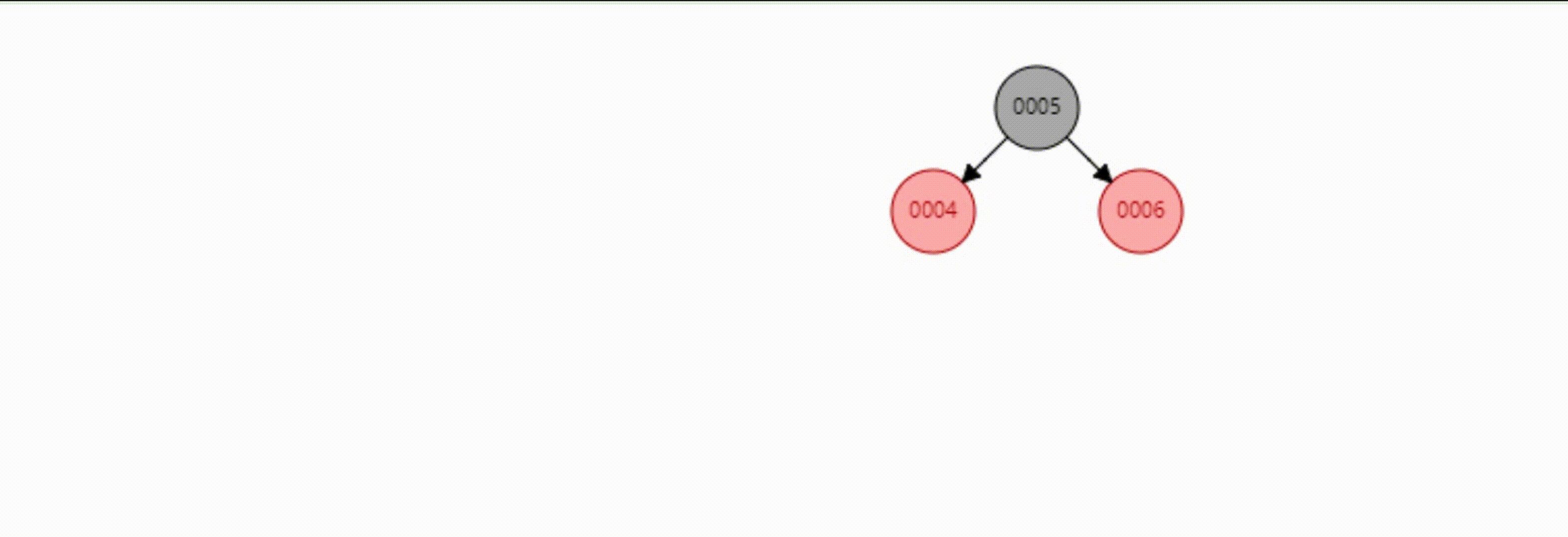
而对于上面的添加还有一种情况需要旋转两次,解决思路就是变换为上面的情况,然后按照上面的步骤完成

而4里面的情况,进行变色即可

如果经过变色爷爷节点变色为红色,假设不是根节点的话,与上面的其他节点发生冲突,我们把变色的爷爷节点当做新增的节点进行操作
如果爷爷节点的父亲节点和叔叔节点都为红色则继续按照上面的操作进行调整,如果叔叔节点不是红色则需要进行其他调整
例如下图,如果4的叔叔节点为红色,那么直接根节点变黑(先变红发现是根节点然后变黑)即可,如果叔叔节点为黑色,那么就需要进行旋转变色操作

删除节点
前驱节点和后继节点
删除一个节点肯定有人要替代被删除节点的位置,可以选择前驱节点或后继节点
前驱节点 : 小于当前节点的最大节点
后继节点 : 大于当前节点的最小节点
例如 下面图的6节点,前驱节点就是5,后继节点就是9
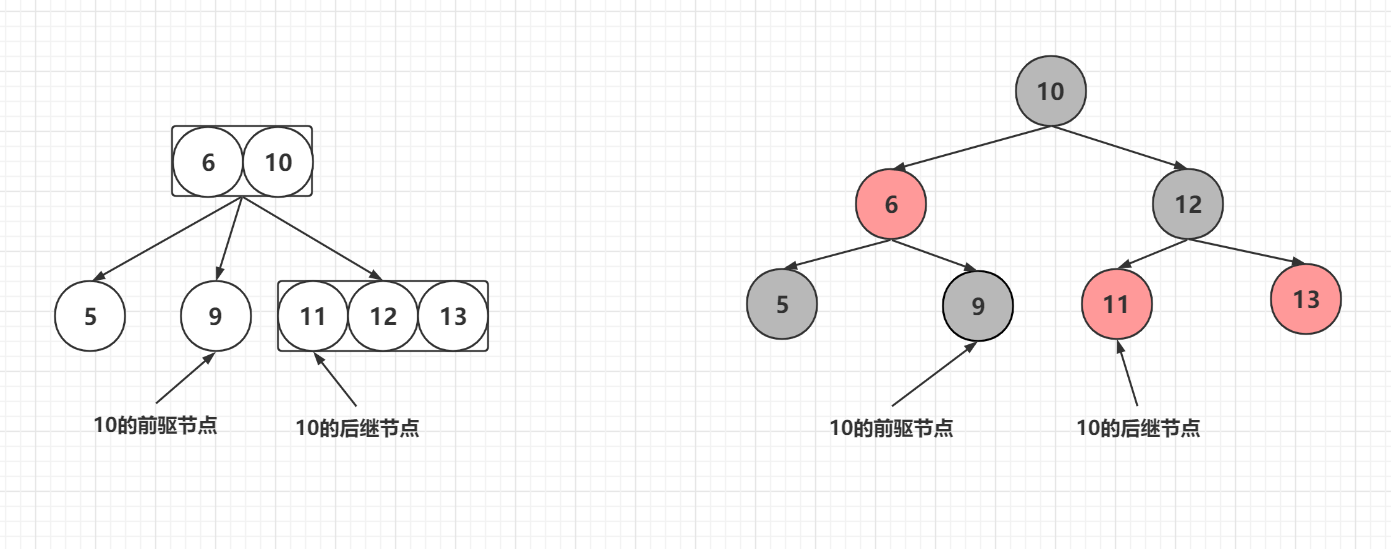
除非左子树或右子树只有一个节点
寻找前驱节点就是寻找左子树的第一个节点的右儿子,一直往右找直到找到没有右子节点的节点
寻找后驱节点就是寻找右子树的第一个节点的左儿子,一直往左找直到找到没有左子节点的节点
删除一个节点可以理解为删除它的替换节点
为什么这么说呢,如果使用代码实现红黑树,一个节点至少有3个指针,左孩子指针,右孩子指针,父亲指针,节点中假设就存储一个值,那么移除原来的节点替换为新的节点需要移动:左右孩子指针,父指针,替换的左右孩子指针,左右孩子的父指针.........
而我们将替换的节点的值赋值给需要删除的节点,还是上面那个图,假如我们删除10,使用后继节点11来替代,我们只需要将11的值赋值给10,然后删除11节点即可,也就是说只需要修改两个指针,11的父指针和12的左孩子指针即可完成
而在234树中,删除的永远都是叶子节点,可以看上面的图,前驱节点和后继节点用于都是在最底层
那么我们删除的情况从是否有孩子来看就只有两种
- 删除没有孩子的节点
- 删除有一个孩子的节点
为什么没有2个孩子的情况呢?如果删除一个节点来寻找它的替换节点,那么要么是前驱或后继,而这两个节点的条件是一直寻找左边孩子或右边孩子,如果一个节点有两个孩子,那么它肯定不是一个前驱或后继节点
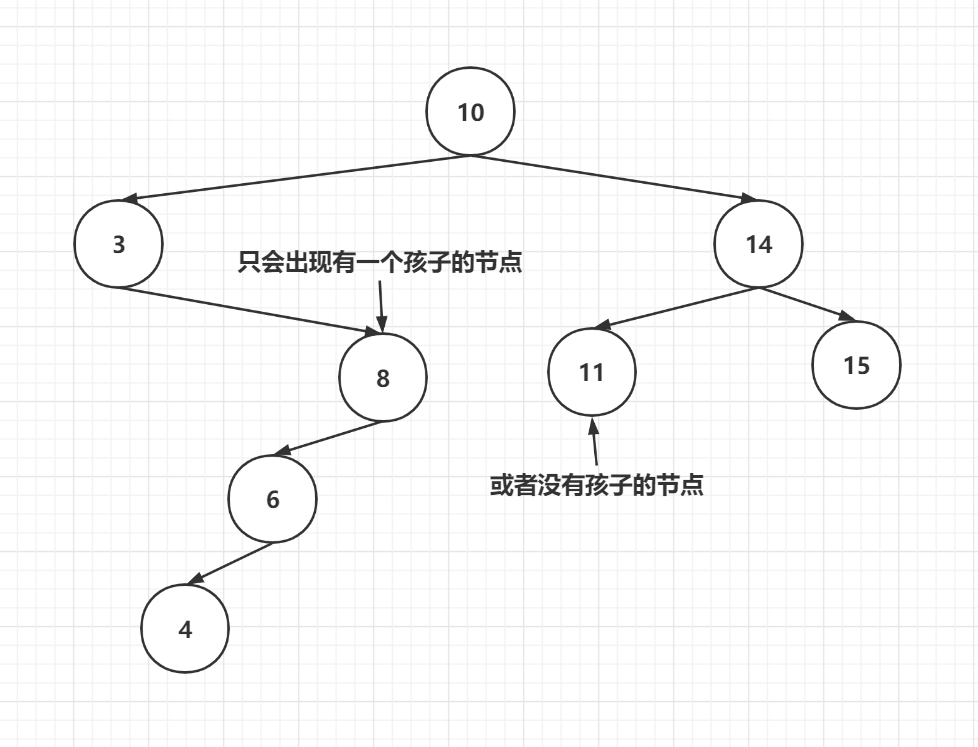
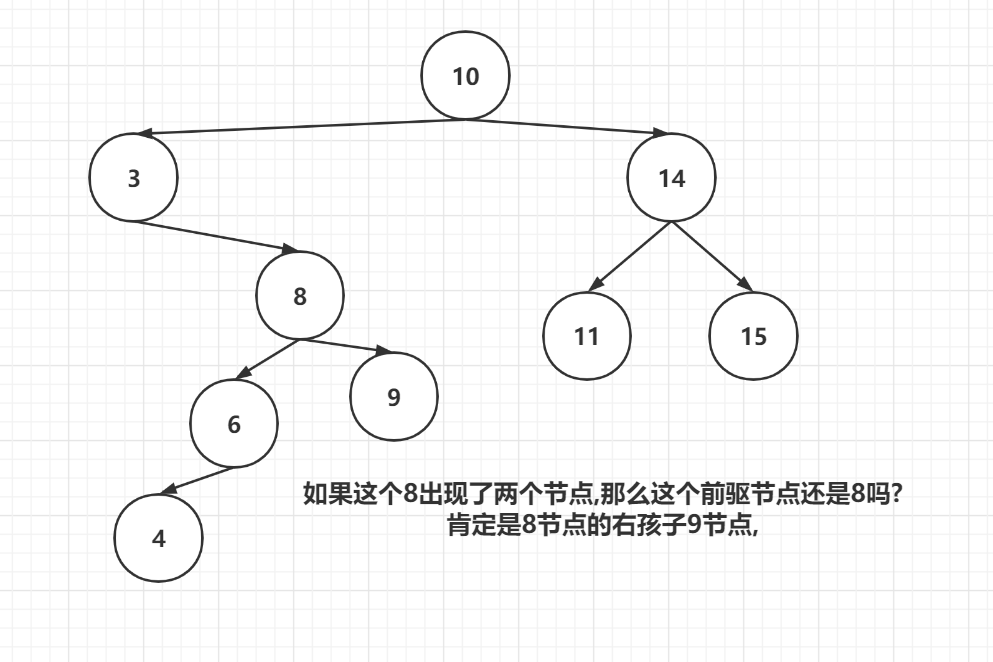
后继节点同理,如果一个前驱节点或后继节点有两个子节点,那么它一定不是前驱节点或后继节点
前驱或后继节点从叶子节点开始的层数不会大于2
那还有个疑问,会不会出现下面这种情况,10的后继节点12这都3层了,不是说不会大于2吗
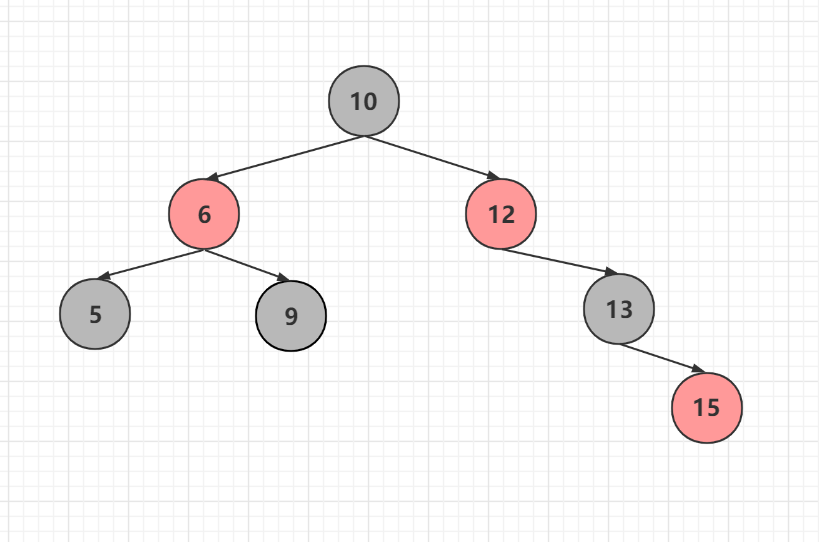
这种情况存在吗?现在都知道红黑树是234树转换来的,那么234树中会出现一个节点只有一个孩子的情况吗?
234树的生长都是从叶子节点进行分裂的,也就是说除了叶子节点,就是说最少的子节点也就是两个,最多4个,不可能出现上图的情况,两个子节点的节点为2-节点,2节点除了第一次添加为根节点或叶子节点以外,任何2-节点都会连接两个子节点,而两个子节点肯定是2,3,4节点其中之一,转换红黑树不可能出现上图情况,可以回去看看234树转换红黑树对应图
那么下面开始进行删除
先在234树上进行删除
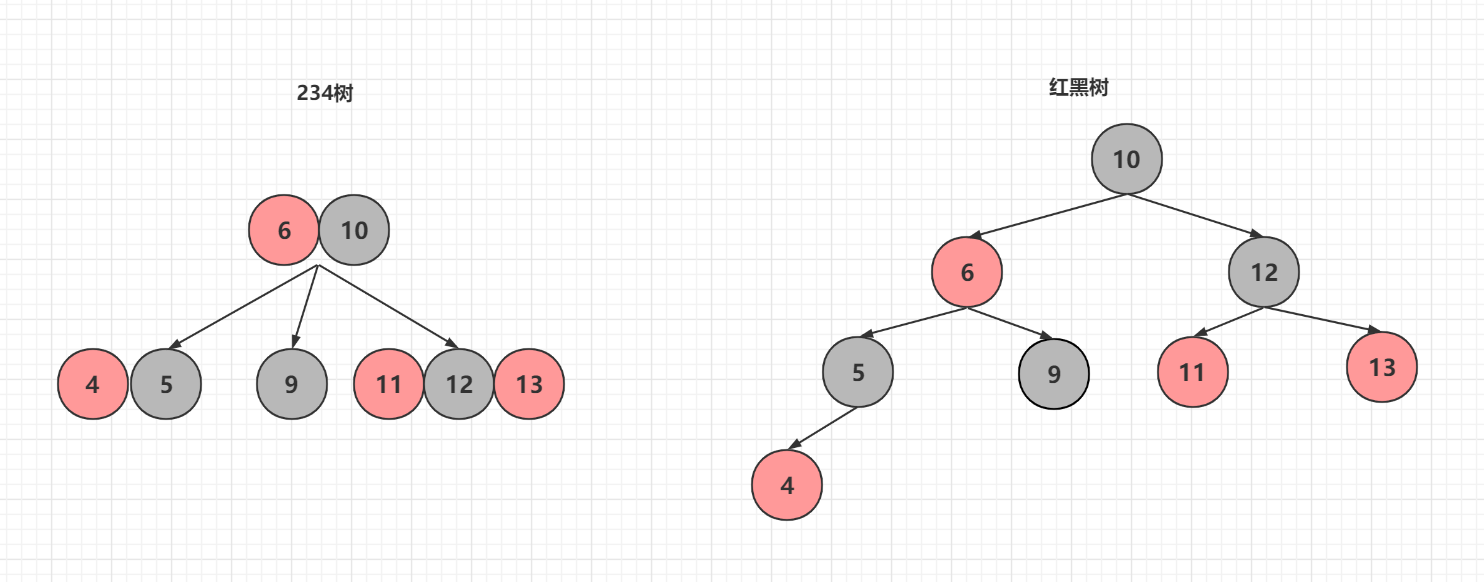
可以直接进行删除的有4,11,13,其中4和5比较特殊,如果进行的是右倾操作,那么可以直接删除5
在234树删除操作中3-节点和4-节点是可以自己搞定的,例如删除4或5, 11或12或13,随便删除一个都不影响234树的性质
而在红黑树中删除只能删除234树对应的3-节点和4节点中红色节点,这几个节点可以直接删除,不需要任何额外操作
在红黑树中删除5只需要将4替换掉5,然后进行变色即可,红黑树的性质依然保持
删除
情况1,自己能搞定,对应234树当前要的删除3-节点或4-节点
-
叶子节点
例如是234树中的红色叶子节点或红黑树中没有子节点的红色节点直接删除
例如上图的红黑树中4,11,13节点,可以直接删除
-
有一个子节点
使用子节点来替代,如果需要进行变色
例如上图的红黑树中5节点,删除后4节点替代自己,然后变黑色,而12节点可以找左儿子或右儿子都可以替换自己
情况2 自己搞不定,需要兄弟节点和父亲节点帮忙
兄弟节点为3-节点的情况
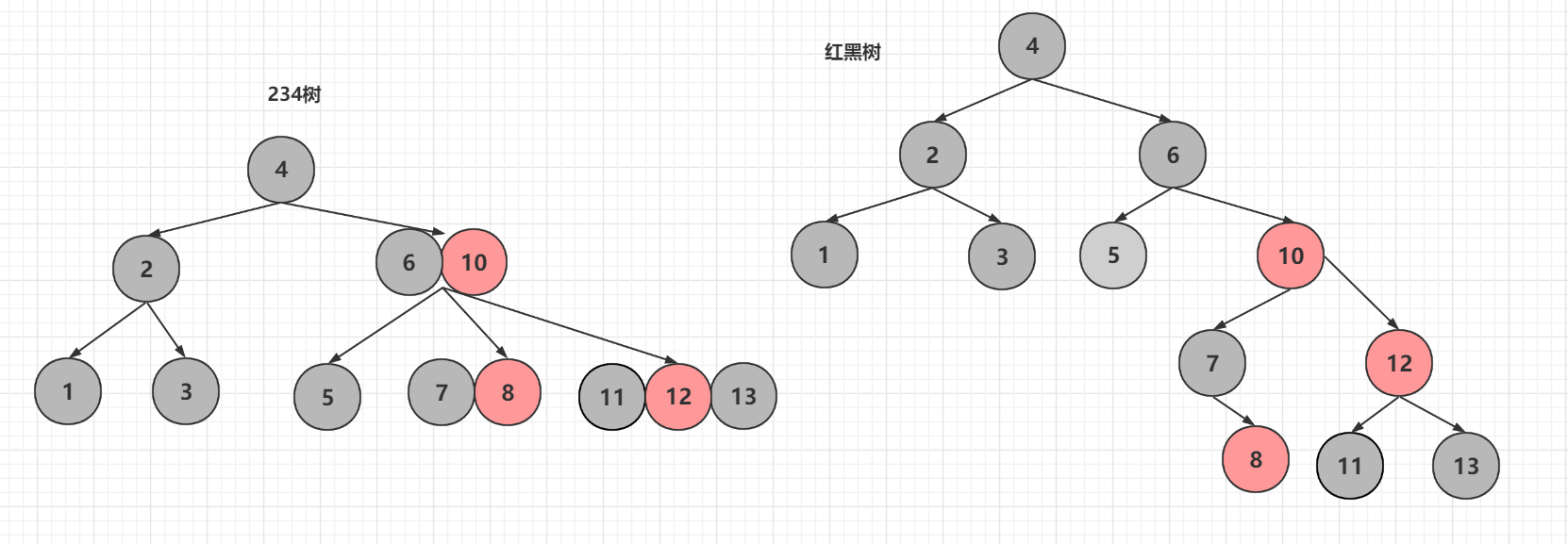
例如现在想要删除5,这时候就需要兄弟节点和父节点帮忙
首先将5删除,之后需要从兄弟节点拿来一个节点来弥补空缺,但是兄弟节点都比6大,如果直接放入无论是234树还是红黑树都会违反性质,234 : 3-节点的左子树元素全部小于key1 ,红黑树: 任何一个节点左边都是小于当前节点
这时我们把父亲节点用来弥补删除的空缺
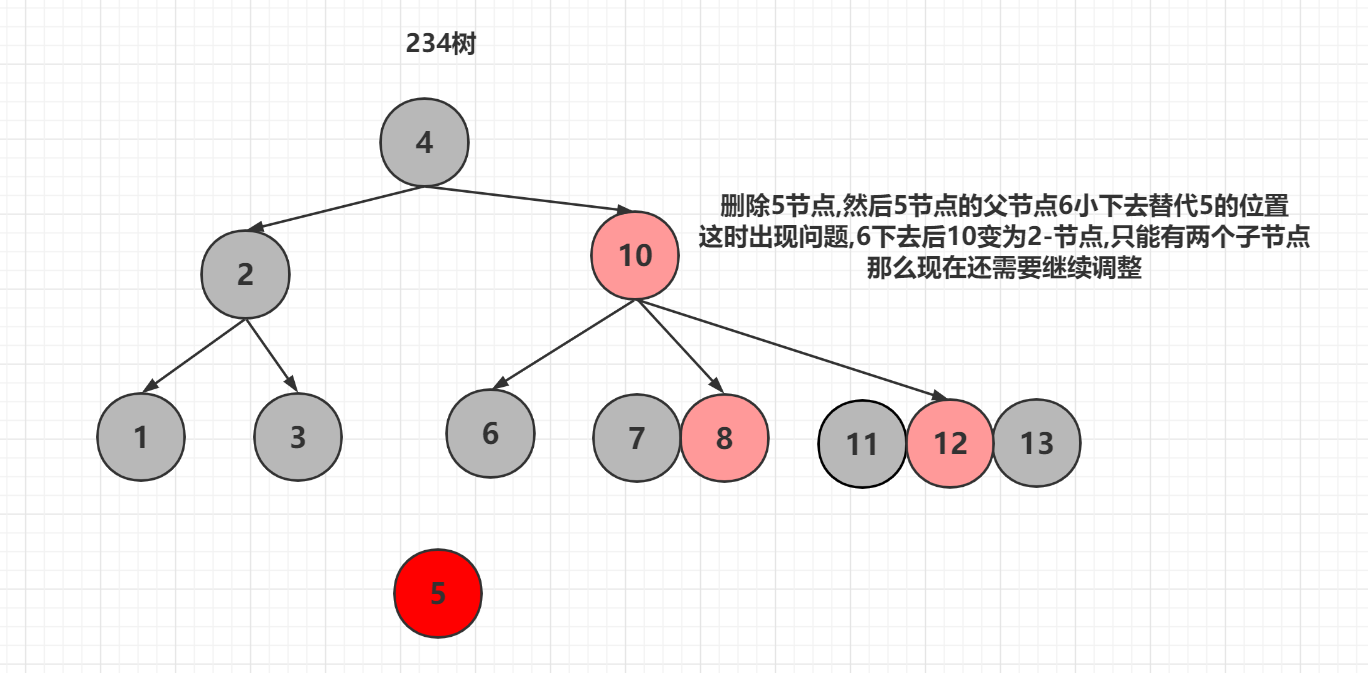
之后兄弟节点去弥补父节点的空缺
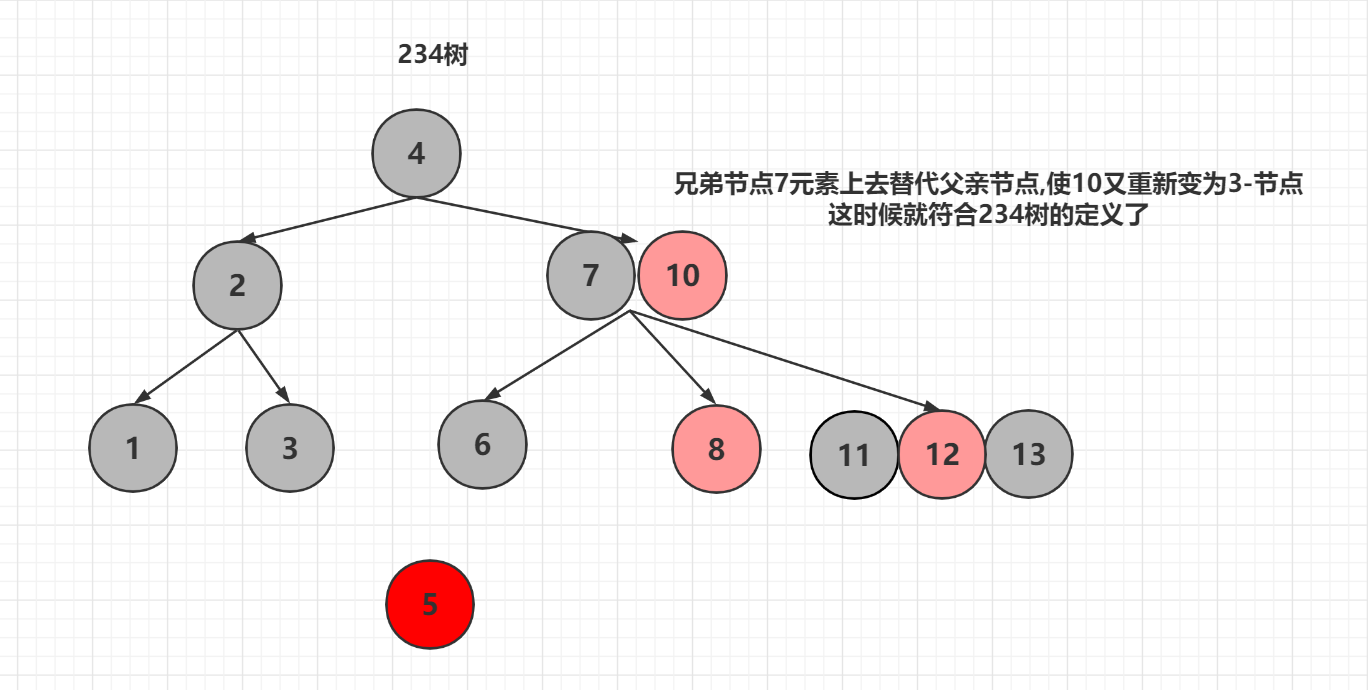
那么回到红黑树呢?
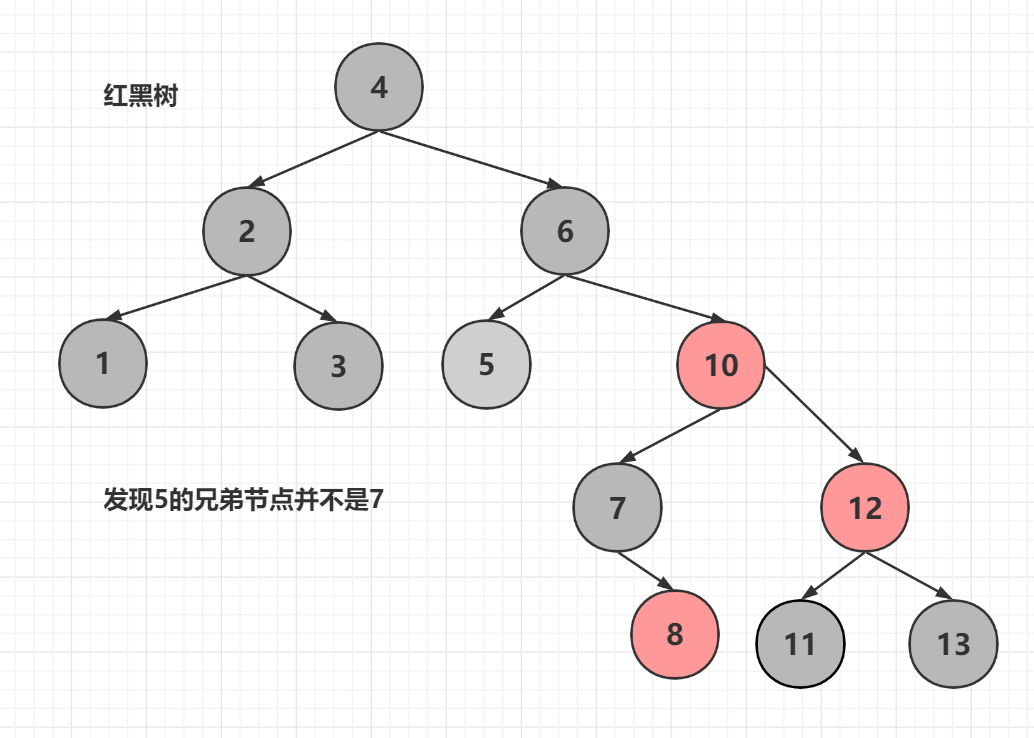
为什么会出现这种情况呢?我们回想一下234树转换红黑树的图,在234树中一个3-节点可能出现左倾或右倾的情况
上面是6在上面10在下面的情况,我们换成相反的情况来看看
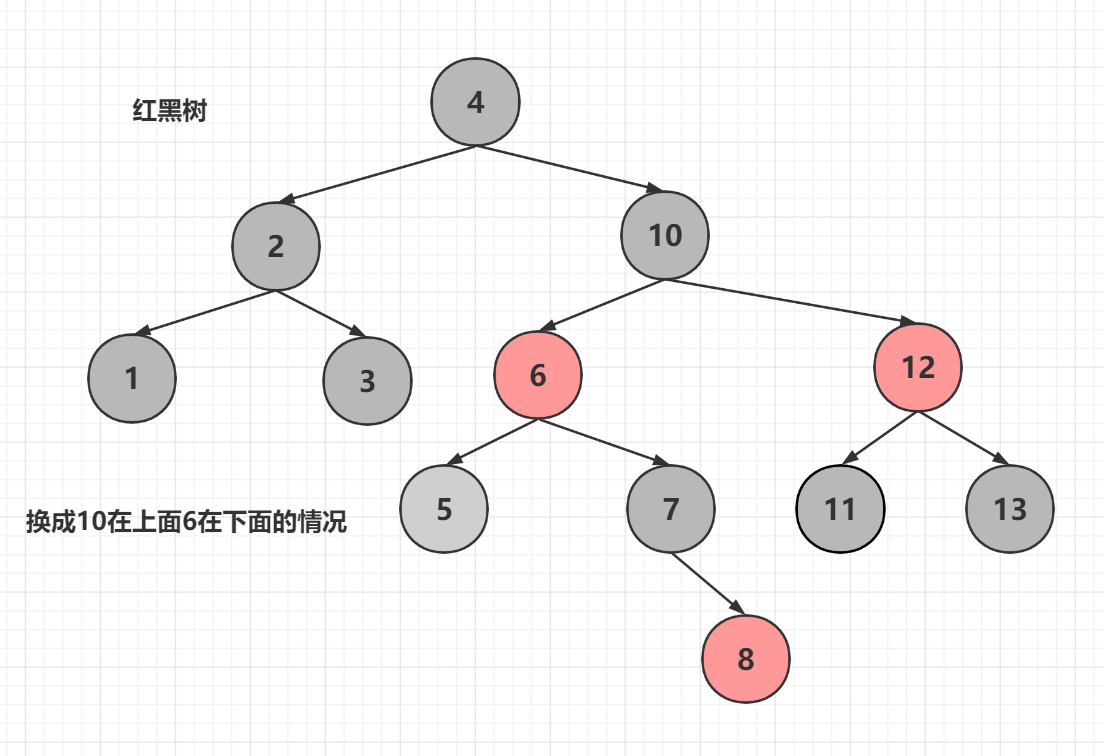
这时5的兄弟节点就和234树中的一样了,234树的3-节点转换为红黑树的两种情况都可以通过左旋变色或右旋变色进行变化
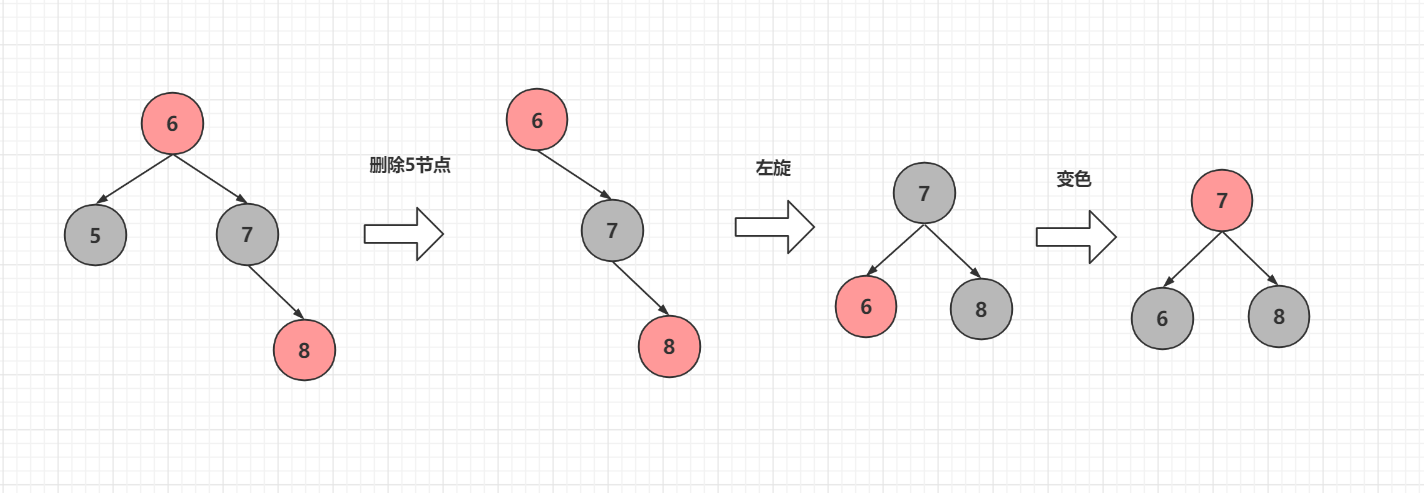
例如上图,我们6和8节点进行右旋,就会变成上面第二张图,而上面的第二张图6节点和8节点进行左旋又会变成上面的这张图
有没有发现一个问题呢,当红黑树5节点的兄弟节点为黑色时也就是说明它的兄弟节点和234树中5节点的兄弟节点一致
也就是说如果它的兄弟节点为红色,需要先进行旋转变色才能进行删除,而6和8变色在234树上等于没动,因为234树根本就没有颜色,只是为了方便对比红黑树添加的颜色
上面的图还有一种情况,就是3-节点7和8位置反的,8在上面7在下面,而替代需要兄弟节点中最小的元素来替代,如果出现这种情况需要先将7和8进行旋转换色,成为上面的情况,然后再进行替换
再来看兄弟节点为4-节点的情况
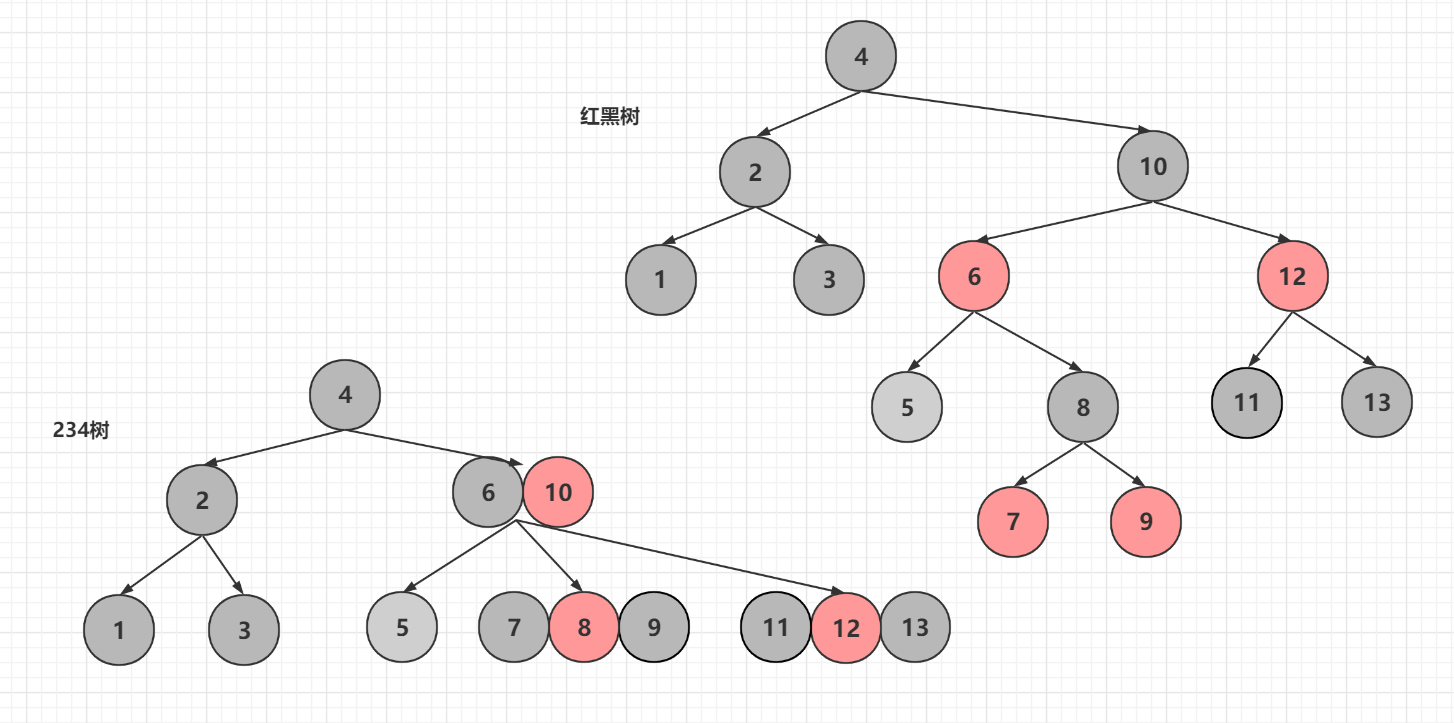
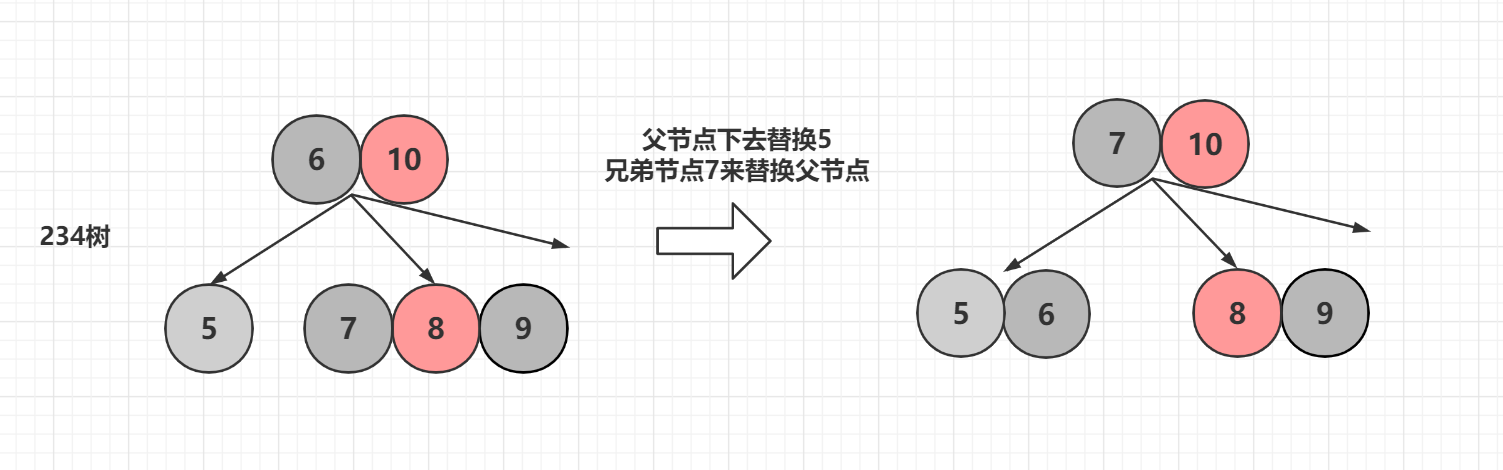
还是删除5节点,离它最近的兄弟节点是个4-节点
兄弟节点为4-节点的删除
只画需要修改的地方,先来看234树
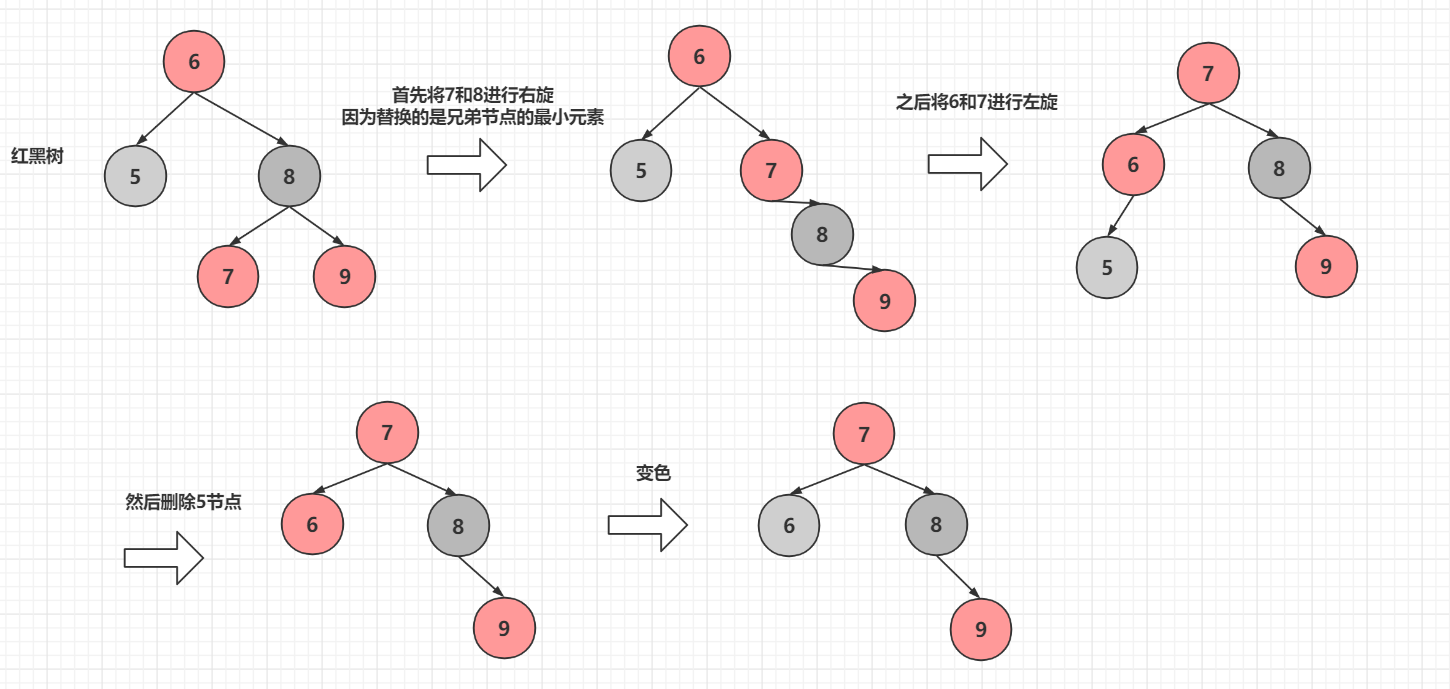
红黑树
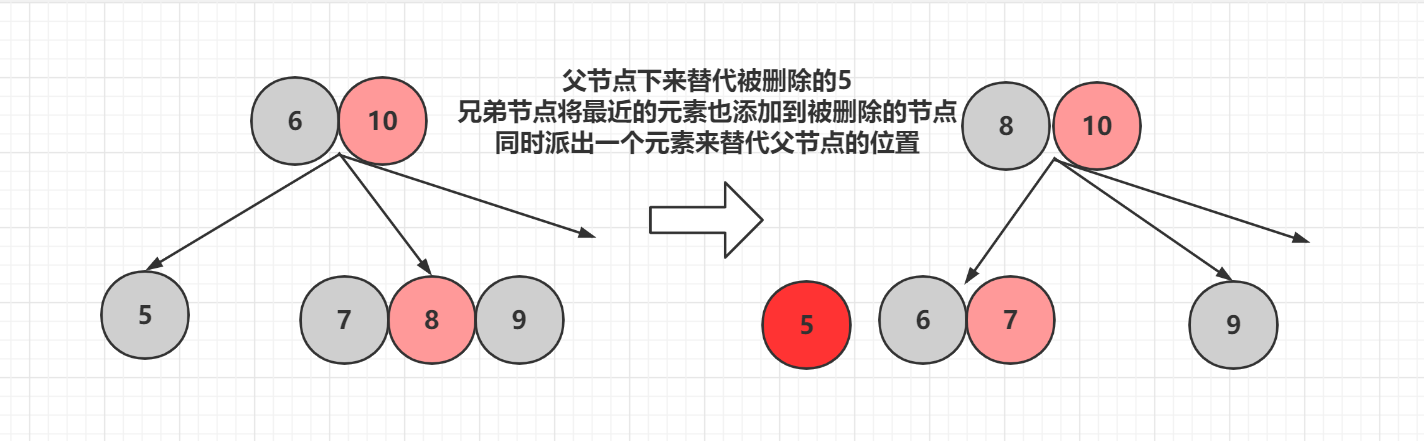
还有一种方法
而对应红黑树就比较简单了
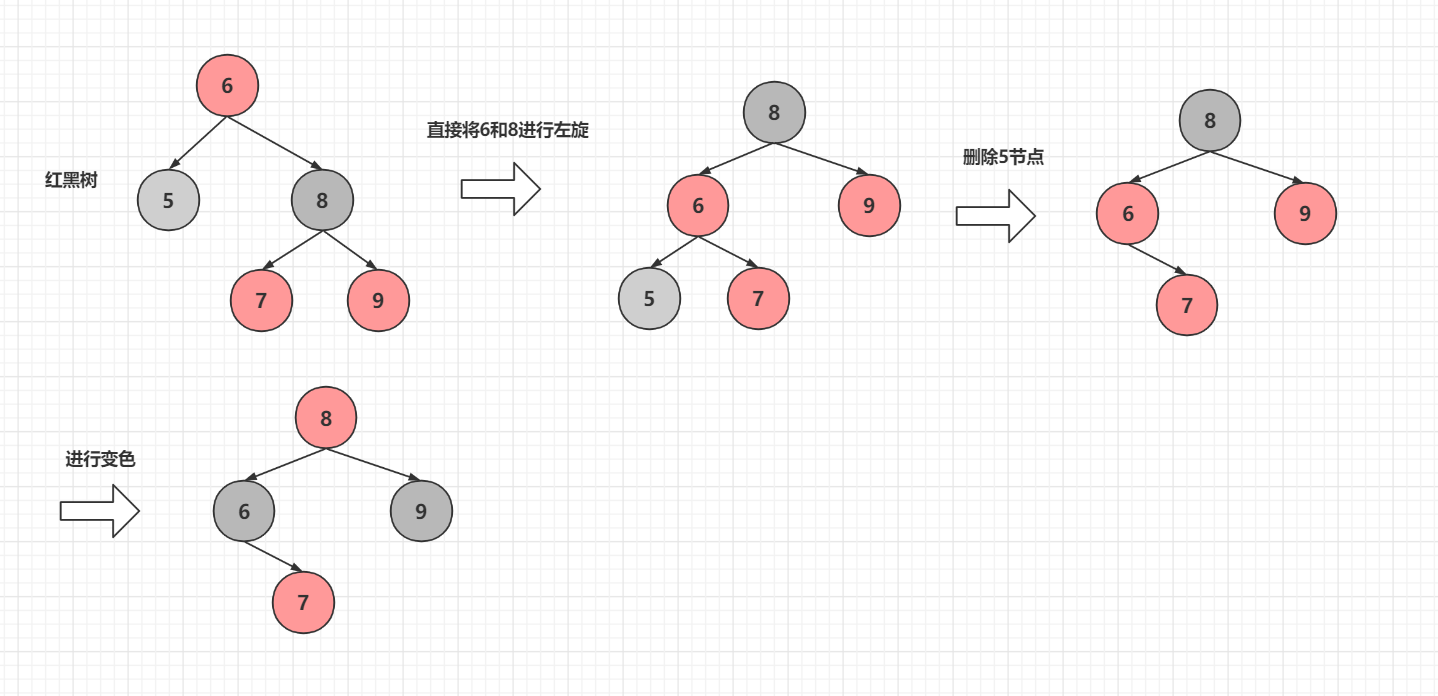
最后关于变色为什么不是8和9变成黑色,因为红黑树必须保证每个叶子节点到根节点经过黑色节点个数相同,同时保证没有两个红色节点相连,如果是8和9变成黑色,为了第一条那么6和7必须变为红色,而变成红色就违反了第二条,上面的删除第一种操作最后的变色同理,如果7和9为黑色,那么从9的叶子节点出发将会比从7的叶子节点多一个黑色节点,违反了红黑树的性质
看个动图加深记忆
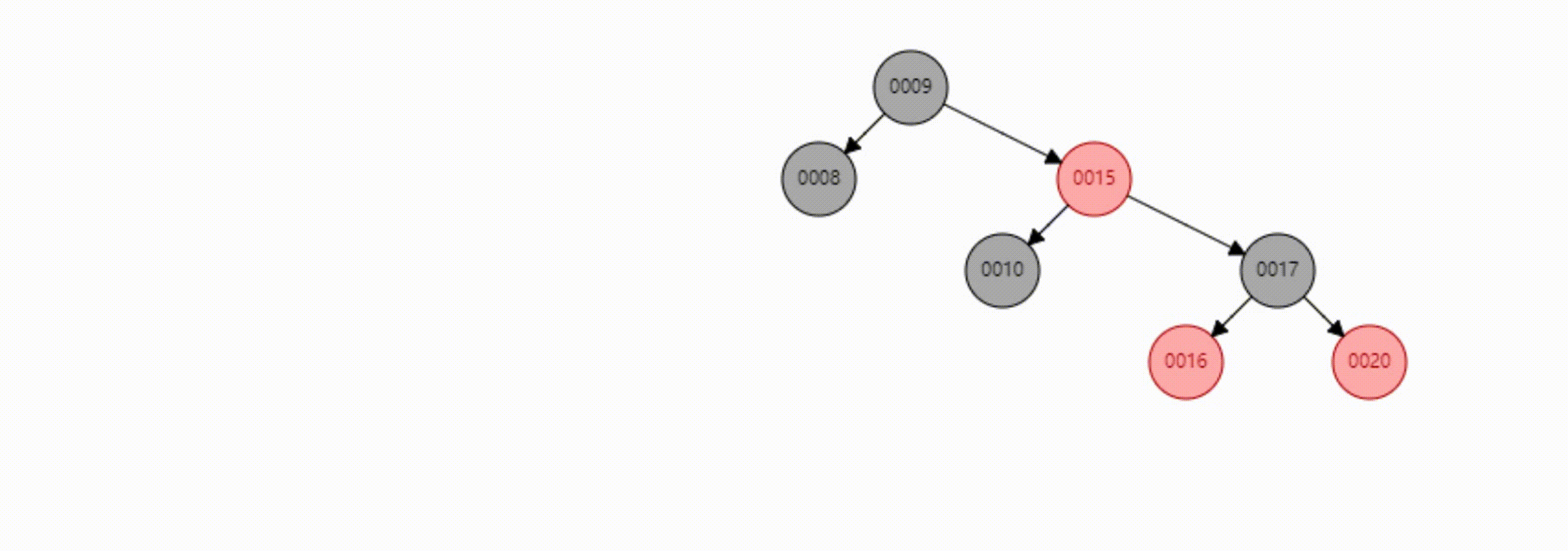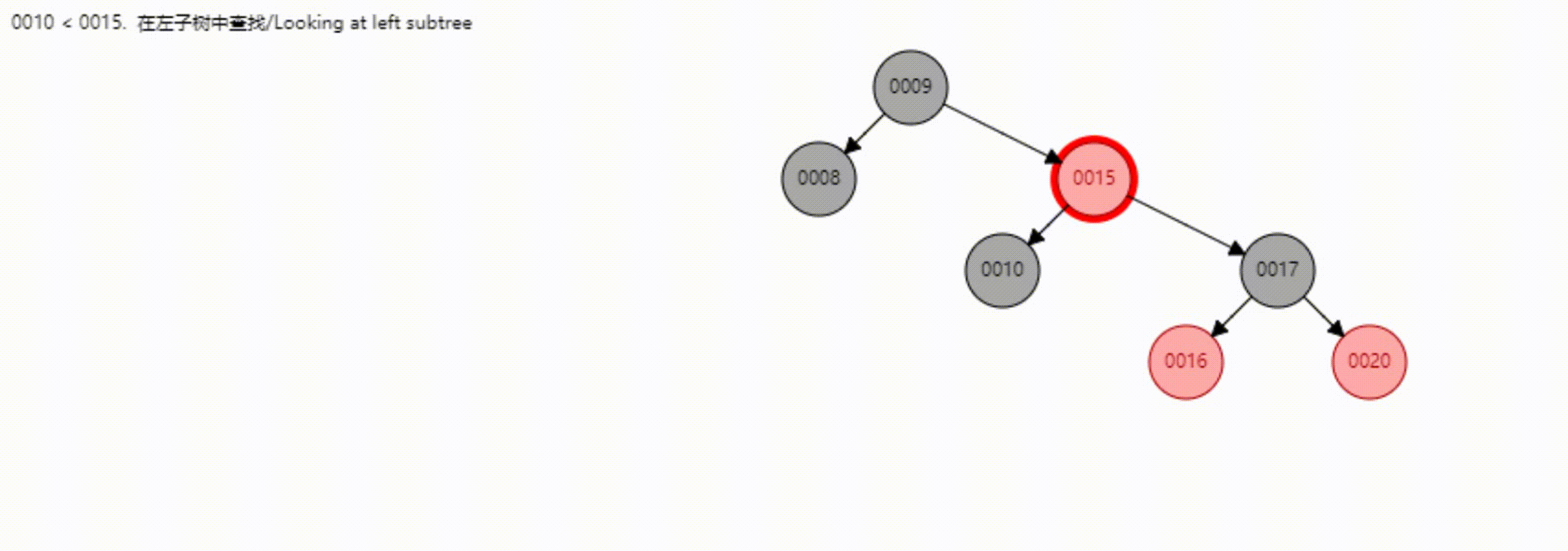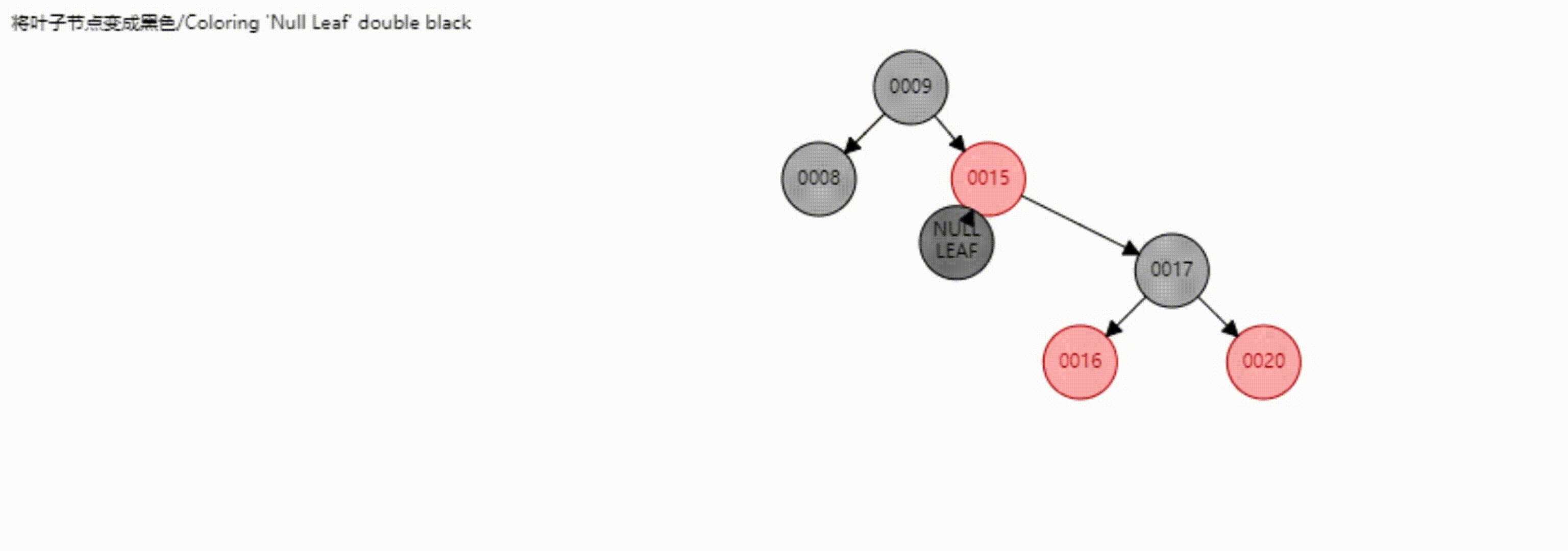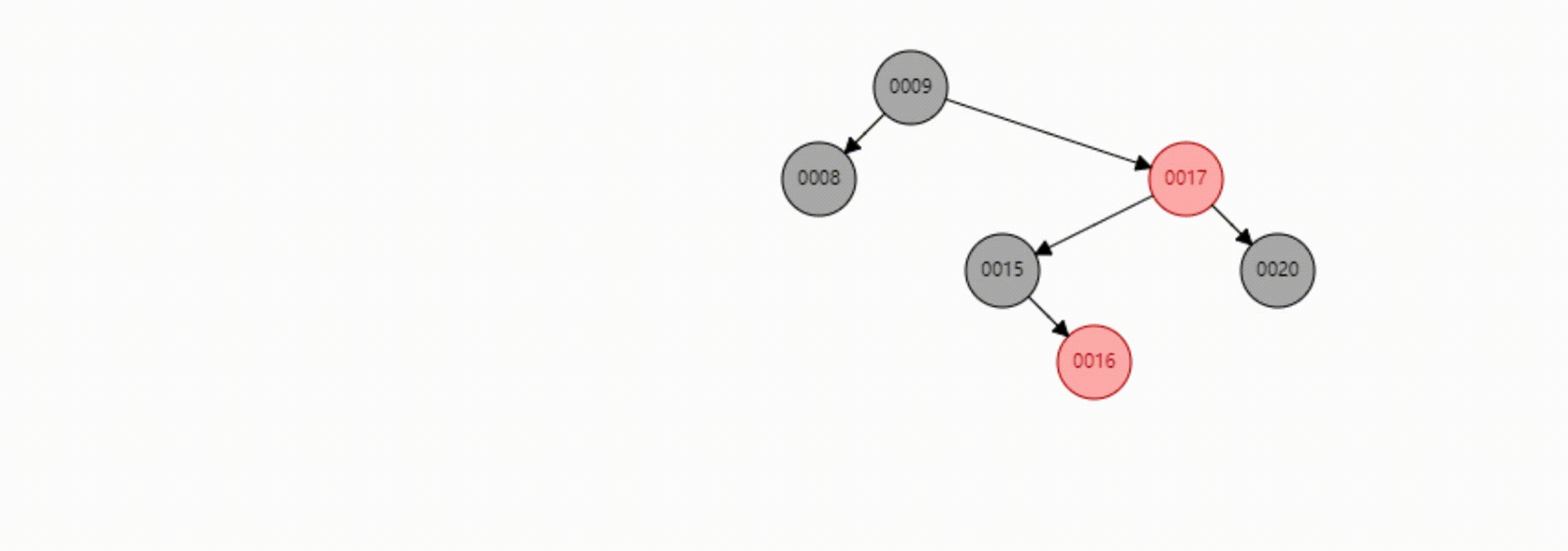
这里使用的是第二种删除方式,因为可以少旋转一次
情况3,自己解决不了,兄弟节点也帮助不了(兄弟节点也没有子节点)
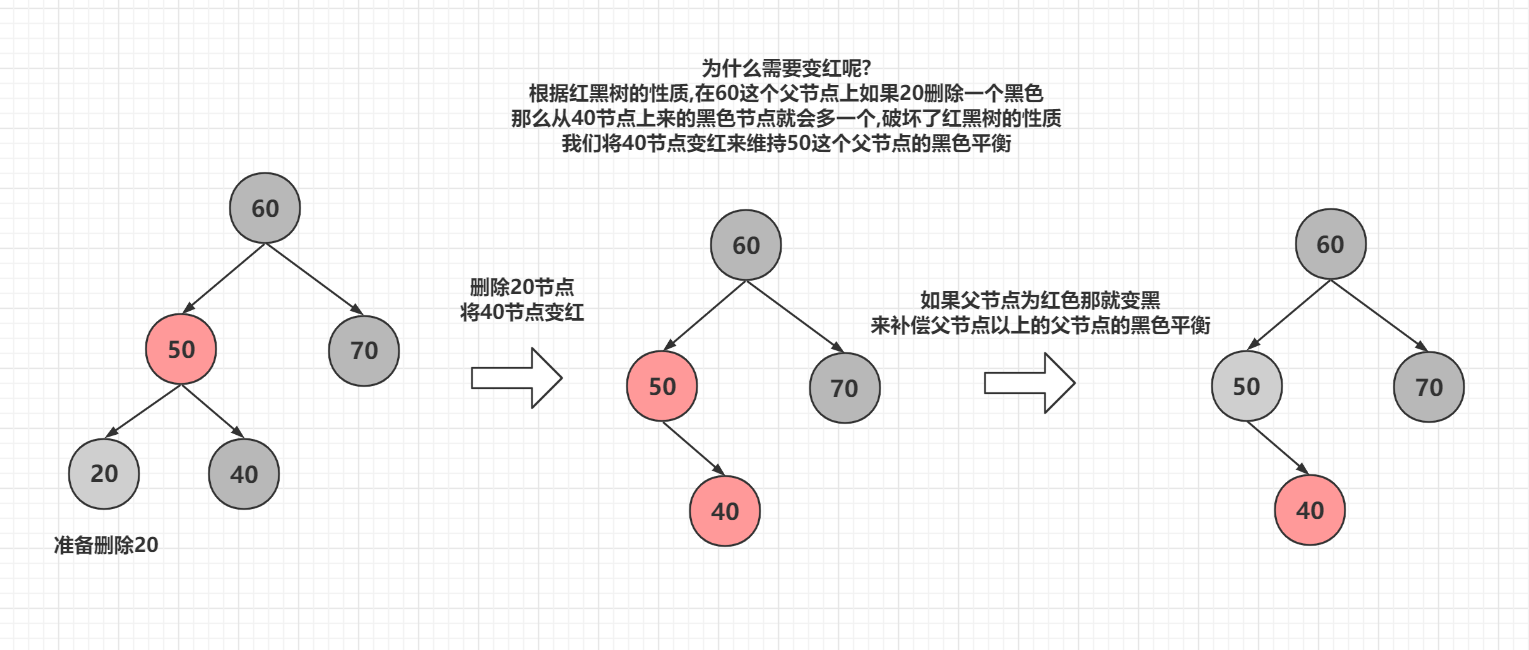
如果父亲不是红色节点呢?没有办法补偿失去的黑色节点?那么就需要往上面将父节点的兄弟节点变为红色,来弥补爷爷节点的黑色平衡,然后将爷爷节点的父节点变黑,但是,如果爷爷节点的父节点也是黑色,那么就需要递归往上进行操作,知道找到父节点不为黑色的节点
进行上面操作后再根据删除节点的父节点,把父节点当做要删除的节点(并不真正删除),根据上面情况进行调整
本文仅个人理解,如果有不对的地方欢迎评论指出或私信,谢谢٩(๑>◡<๑)۶


 浙公网安备 33010602011771号
浙公网安备 33010602011771号