DS博客作业03--树
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业03--树 |
| 这个作业的目标 | 学习树结构设计及运算操作 |
| 姓名 | 黄抒鸿 |
0.PTA得分截图

1.本周学习总结(5分)
树的基本术语:
·根--及根结点(没有前驱)
·叶子--即终端结点(没有后继)
·森林--指m棵不相交的树的集合
·有序树--结点各子树从左至右有序,不能互换
·无序树--结点各子树可互换位置
·双亲--即上层的那个结点(直接前驱)
·孩子--即下层结点的子树的根(直接后继)
·兄弟--同一双亲下的同层结点(孩子之间互称兄弟)
·祖先--即从根到该结点所经分支的所有结点
·子孙--即该点下层子树中的任一结点
·结点--即树的数据元素
·结点的度--结点挂接的子树数,分支数目
·结点的层次--从根到该结点的层数(根结点算第一层)
·终端结点--即度为0的结点,即叶子
·分支结点--即度不为0的结点(内部结点)
·树的深度--指所有结点中最大的层数
1.1 二叉树结构
定义:二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个结点
·二叉树的五种基本形态
空二叉树
只有一个根结点
根结点只有左子树
根结点只有右子树
左右子树均不为空树
·二叉树性质
1)非空二叉树上叶结点数等于双分支节点数+1
2)在二叉树的第i层上至多有2^(i-1)个结点(i>=1)
3)高度为h的二叉树至多有2^h-1个结点(h>=1)
4)具有n个结点的完全二叉树的深度必为[log(2,n)]min+1
1.1.1 二叉树的2种存储结构
树的顺序存储和链式存储结构,并分析优缺点。
1.1.1.1顺序存储
·完全二叉树:对一颗具有n个结点的二叉树按层序遍历,如果编号i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这颗二叉树称为完全二叉树
·满二叉树:在一颗二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树
二叉树的顺序存储指的是使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。
普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些节点,将其"拼凑"成完全二叉树即可。如图 1 所示:
图 1 中普通二叉树的数组存储状态如图所示:
完全二叉树的顺序存储,仅需从根节点开始,按照层次依次将树中节点存储到数组即可。
完全二叉树示意图:
存储状态如图:
二叉树顺序存储结构缺点
·对于完全二叉树来说,其顺序存储是十分合适的
·对于普通二叉树来说:在最坏的情况下,一个深度为k且只有k个结点的单支树(树中不存在度为2的结点)却需要2^k-1的一维数组。空间利用率太低
·数组,查找、插入删除不方便。
1.1.1.2链式存储
如图 1 所示,此为一棵普通的二叉树,若将其采用链式存储,则只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可。因此,图 1 对应的链式存储结构如图 2 所示:


结构定义:
//二叉树的链表结构
typedef char ElementType;/* 所有ElementType等同于char */
typedef TNode* Position;
typedef Position BinTree;/* 二叉树类型 */
struct TNode {
ElementType Data; /* 结点数据 */
BinTree Left; /* 指向左子树 */
BinTree Right; /* 指向右子树 */
};
二叉树链式存储优缺点
优点:读取某个指定节点的时候效率偏低O(nlogn)
缺点:相对二叉树比较大的时候浪费空间较少
二叉树的顺序存储,寻找后代节点和祖先节点都非常方便,但对于普通的二叉树,顺序存储浪费大量的存储空间,同样也不利于节点的插入和删除。因此顺序存储一般用于存储完全二叉树。
链式存储相对顺序存储节省存储空间,插入删除节点时只需修改指针,但寻找指定节点时很不方便。不过普通的二叉树一般是用链式存储结构。
1.1.2 二叉树的构造
总结二叉树的几种构造方法。分析你对这些构造方法的看法。务必介绍如何通过先序遍历序列和中序遍历序列、后序遍历序列和中序遍历序列构造二叉树。
1.先序
BTree CreateBT(string str,int&i)
{
if(i>=len-1)
return NULL;
if(str[i]=='#')
return NULL;
BTree bt=new BTnode;
bt->data=str[i];
bt->lchild=CreateBT(str,++i);
bt->rchild=CreateBT(str,++i);
}
2.中序
BTree CreateBT(string str,int&i)
{
if(i>=len-1)
return NULL;
if(str[i]=='#')
return NULL;
BTree bt=new BTnode;
bt->lchild=CreateBT(str,++i);
bt->data=str[i];
bt->rchild=CreateBT(str,++i);
}
3.后序
BTree CreateBT(string str,int&i)
{
if(i>=len-1)
return NULL;
if(str[i]=='#')
return NULL;
BTree bt=new BTnode;
bt->lchild=CreateBT(str,++i);
bt->rchild=CreateBT(str,++i);
bt->data=str[i];
}
1.1.3 二叉树的遍历
总结二叉树的4种遍历方式,如何实现。
二叉树的先序遍历(DLR)
先序遍历的递归过程为:若二叉树为空,遍历结束。否则,
(1)访问根结点;
(2)先序遍历根结点的左子树;
(3)先序遍历根结点的右子树。
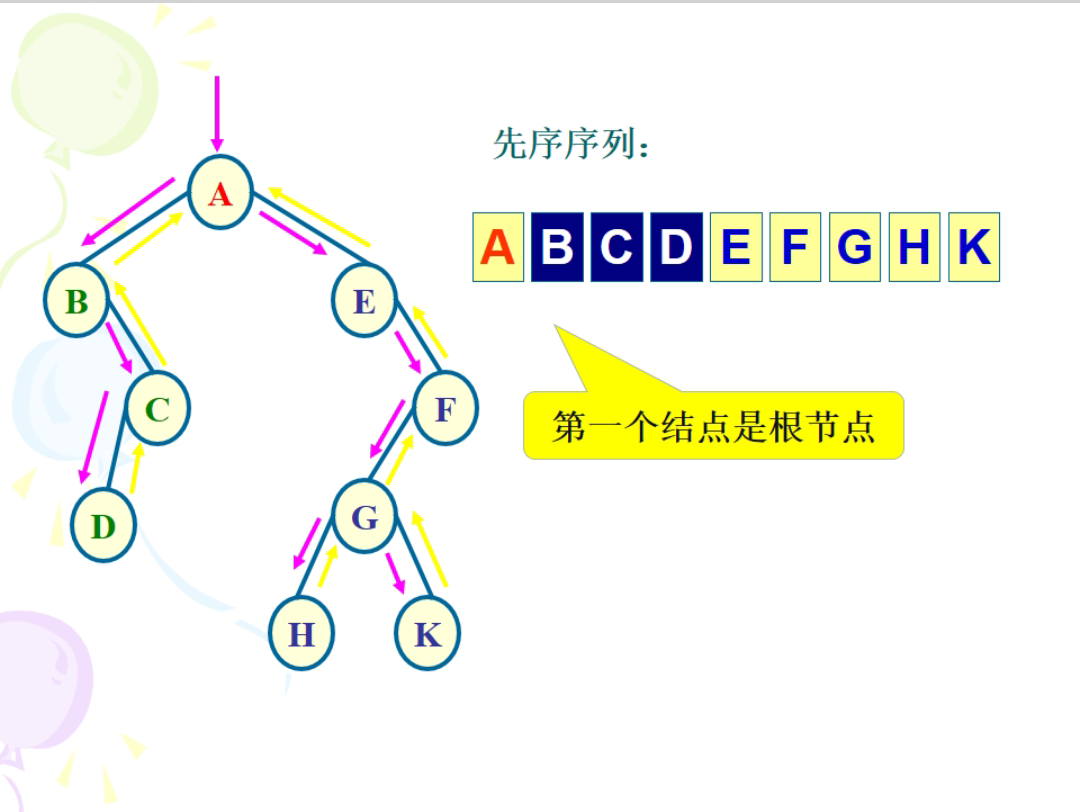
先序遍历二叉树的递归算法如下:
void PreOrder(BTree bt)
{
if (bt != NULL)
{
printf("%c", bt->data);
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
二叉树的中序遍历(LDR)
中序遍历的递归过程为:若二叉树为空,遍历结束。否则,
(1)中序遍历根结点的左子树;
(2)访问根结点;
(3)中序遍历根结点的右子树。

中序遍历二叉树的递归算法如下:
void InOrder(BTree bt)
{
if (bt!= NULL)
{
InOrder(bt->lchild);
printf("%c", bt->data);
InOrder(bt->rchild);
}
}
二叉树的后序遍历(LRD)
后序遍历的递归过程为:若二叉树为空,遍历结束。否则,
(1)后序遍历根结点的左子树;
(2)后序遍历根结点的右子树。
(3)访问根结点;

后序遍历二叉树的递归算法如下:
void PostOrder(BTree bt)
{
if (bt != NULL)
{
PostOrder(bt->lchild);
PostOrder(bt->rchild);
printf("%c", b->data);
}
}
层次遍历
在进行层次遍历时,对某一层的节点访问完后,再按照它们的访问次序对各个节点的左、右孩子顺序访问。
初始化队列,先将根节点进队。
while(队列不空)
{
队列中出列一个节点*p,访问它;
若它有左孩子节点,将左孩子节点进队;
若它有右孩子,将右孩子进队。
}
代码:
void LevelOrder(BTNode* b)
{
BTNode* p;
SqQueue* qu;
InitQueue(qu);
enQueue(qu, b);
while (!QueueEmpty(qu))
{
deQueue(qu, p);
printf("%c", p->data);
if (p->lchild != NULL)
enQueue(qu, p->lchild);
if (p->rchild != NULL)
enQueue(qu, p->rchild);
}
}
1.1.4 线索二叉树
定义:对于n个结点的二叉树,在二叉链存储结构中有n+1个空链域,利用这些空链域存放在某种遍历次序下该结点的前驱结点和后继结点的指针,这些指针称为线索,加上线索的二叉树称为线索二叉树。
线索二叉树如何设计?
记ptr指向二叉链表中的一个结点,以下是建立线索的规则:
(1)如果ptr->lchild为空,则存放指向中序遍历序列中该结点的前驱结点。这个结点称为ptr的中序前驱;
(2)如果ptr->rchild为空,则存放指向中序遍历序列中该结点的后继结点。这个结点称为ptr的中序后继;
显然,在决定lchild是指向左孩子还是前驱,rchild是指向右孩子还是后继,需要一个区分标志的。因此,我们在每个结点再增设两个标志域ltag和rtag,注意ltag和rtag只是区分0或1数字的布尔型变量,其占用内存空间要小于像lchild和rchild的指针变量。结点结构如下所示:

其中ltag为0时指向该结点的左孩子,为1时指向该结点的前驱;rtag为0时指向该结点的右孩子,为1时指向该结点的后继;


线索二叉树结构的实现:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
using namespace std;
typedef struct Binode
{
char data;
struct Binode *lchild,*rchild;
int ltag,rtag;
} Binode,*Bitree;
Bitree pre;
void CreatTREE(Bitree &T)
{
char ch;
scanf("%c",&ch);
if(ch==' ')
{
T=NULL;
}
else
{
T=(Bitree)malloc(sizeof(Binode));
T->data=ch;
T->ltag=0;
T->rtag=0;
CreatTREE(T->lchild);
CreatTREE(T->rchild);
}
return;
}
void travel_threadtree(Bitree H) //中序遍历线索树 从头节点开始
{
Bitree p;
p=H->lchild; //p为二叉树头节点
while(p!=H)
{
while(p->ltag==0) //有左子树 则 一直往下
p=p->lchild;
printf("%c ",p->data);
while(p->rtag==1&&p->rchild!=H) //根据它的线索一直往后输出
{
p=p->rchild;
printf("%c ",p->data);
}
p=p->rchild; //当没有线索时 表示有右子树
}
return;
}
void thread(Bitree T) //线索化
{
if(T)
{
thread(T->lchild);
if(!T->lchild)
{
T->ltag=1;
T->lchild=pre;
}
if(!pre->rchild)
{
pre->rtag=1;
pre->rchild=T;
}
pre=T; //顺序是左子树 节点 右子树的中序遍历 所有 放这里
thread(T->rchild);
}
return;
}
void threading_(Bitree &H,Bitree T) //新增头节点
{
H=(Bitree)malloc(sizeof(Binode));
H->rchild=H;
H->rtag=0;
if(!T) //二叉树为空
{
H->lchild=H;
H->ltag=0;
}
else
{
pre=H;
H->lchild=T;
H->ltag=0;
thread(T);
H->rtag=1;
H->rchild=pre; //
pre->rchild=H; // 构成循环 以备跳出
}
return;
}
int main()
{
Bitree T,H;
CreatTREE(T);
threading_(H,T);
travel_threadtree(H);
return 0;
}
中序线索二叉树
·头结点左孩子指向根节点
·右孩子为线索,指向最后一个孩子
·遍历序列第一个结点前驱为头结点,最后一个结点后继为头结点
TBTNode* pre;//全局变量
void Thread(TBTNode*& p)//对二叉树p进行中序线索化
{
if (p != NULL)
{
Thread(p->lchild);//左子树线索化
if (p->lchild == NULL)//左孩子不存在,进行前驱结点线索化
{
p->lchild = pre;//建立当前结点的前驱结点线索
p->ltag = 1;
}
else//p结点的左子树已线索化
p->ltag = 0;
if (pre->rchild == NULL)//对pre的后继结点线索化
{
pre->rchild = p;//建立前驱结点的后继结点线索
pre->rtag = 1;
}
else
p->rtag = 0;
pre = p;
Thread(p->rchild);//右子树线索化
}
}
TBTNode* CreateThread(TBTNode* b)//中序线索化二叉树
{
TBTNode* root;
root = (TBTNode*)malloc(sizeof(TBTNode));//创建头结点
root->ltag = 0; root->rtag = 1;
root->rchild = b;
if (b == NULL)//空二叉树
root->lchild = root;
else
{
root->lchild = b;
pre = root;//pre是结点p的前驱结点,供加线索用
Thread(b);//中序遍历线索化二叉树
pre->rchild = root;//最后处理,加入指向头结点的线索
pre->rtag = 1;
root->rchild = pre;//头结点右线索化
}
return root;
}
线索二叉树的好处就在于利用了多余的空区域,使之指向前驱或后继,这就使寻找结点的前驱和后继更加方便。
1.1.5 二叉树的应用--表达式树
建立表达式树的一种方法是每次找到最后的运算符,然后递归建树。 “最后计算”的运算符是在括号外的、优先级最低的运算符。 如果有多个,根据结合性来选择:左结合的 (如加减乘除)选最右边;右结合的 (如乘方)选最左边。
·构造表达式树
void InitExpTree(BTree &T,string str)
{
stack<BTree> s;
stack<char> op;
op.push('#');
int i=0;
while(str[i])
{
if(!In(str[i]))
{
T = new BTNode;
T->data = str[i++];
T->lchild = T->rchild = NULL;
s.push(T);
}
else
{
switch(Precede(op.top(),str[i]))
{
case '<':
op.push(str[i]);
i++;
break;
case '=':
op.pop();
i++;
break;
case '>':
T = new BTNode;
T->data = op.top();
T->rchild = s.top();
s.pop();
T->lchild = s.top();
s.pop();
s.push(T);
op.pop();
break;
}
}
}
while(op.top()!='#')
{
T=new BTNode;
T->data = op.top();
T->rchild = s.top();
s.pop();
if(!s.empty())
{
T->lchild = s.top();
s.pop();
}
s.push(T);
op.pop();
}
T = s.top();
}
·计算表达式树
double EvaluateExTree(BTree T)
{
double sum=0,a,b;
if(!T->lchild && !T->rchild)
{
return T->data-'0';
}
b = EvaluateExTree(T->rchild);
a = EvaluateExTree(T->lchild);
//b = EvaluateExTree(T->rchild);
switch(T->data)
{
case '+':
return a+b;
break;
case '-':
return a-b;
break;
case '*':
return a*b;
break;
case '/':
if(b==0)
{
cout << "divide 0 error!" << endl;
exit(0);
}
return a/b;
break;
}
}
1.2 多叉树结构
1.2.1 多叉树结构
·孩子兄弟链结构
树结构中,位于同一层的节点之间互为兄弟节点。例如,图 1 的普通树中,节点 A、B 和 C 互为兄弟节点,而节点 D、E 和 F 也互为兄弟节点。
孩子兄弟表示法,采用的是链式存储结构,其存储树的实现思想是:从树的根节点开始,依次用链表存储各个节点的孩子节点和兄弟节点。
因此,该链表中的节点应包含以下 3 部分内容(如图 2 所示):
节点的值;
指向孩子节点的指针;
指向兄弟节点的指针;


存储的结果:

树的儿子兄弟表示法结构定义:
typedef struct CSNode
{
TElemType data;
struct CSNode* firstchild, * rightsib;
}CSNode,*CSTree;
1.2.2 多叉树遍历
介绍先序遍历做法:若树不空,则先访问根结点,然后依次先根遍历各棵子树。
class Solution
{
// private int branch = 0;//没有必要声明为成员变量,声明成成员变量还会出错,成员变量可以被多个递归函数共享,在递归中一层修改,上层下层1都会改变
private List<Integer> nodeList = new ArrayList<>();
public List<Integer> preorder(Node root)
{
helper(root);
return nodeList;
}
public void helper(Node root)
{
if(root == null)
{
return ;
}
nodeList.add(root.val);
int branch = root.children.size();
for(int i = 0; i < branch; i++)
{
helper(root.children.get(i));
}
}
}
//结构体
typedef struct st_OriTree
{
int levelValue; //树的level
int orderValue; //排序值
QString nameValue; //当前节点名称
QString preNameValue; //前置节点名称
QMultiMap< int, st_OriTree *> childrenList; //子节点列表
}OriTree;
//创建多叉树
void appendTreeNode(OriTree **head, OriTree node)
{
if (*head == nullptr)
return;
QQueue< OriTree*> queue;
queue.append(*head);
bool isExist = false;
OriTree* p = nullptr;
OriTree* q = *head;
while (!queue.isEmpty())
{
p = queue.front();
queue.pop_front();
if (p != nullptr)
{
for (int i = 0; i < p->childrenList.count(); i++)
{
if (p->childrenList.values().at(i)->preNameValue == node.preNameValue
&& p->childrenList.values().at(i)->levelValue == node.levelValue)
{
if (p->childrenList.values().at(i)->nameValue == node.nameValue)
{
isExist = true;
break;
}
continue;
}
if (p->childrenList.values().at(i)->levelValue == node.levelValue - 1
&& p->childrenList.values().at(i)->nameValue == node.preNameValue)
{
q = p->childrenList.values().at(i);
}
queue.append(p->childrenList.values().at(i));
}
}
}
if (!isExist && q!= nullptr)
{
//create new node
OriTree * newNode = new OriTree();
if (newNode == nullptr || p == nullptr)
{
qDebug() << "new OriTree node failed , node Name :" << node.nameValue;
return;
}
newNode->feedValue = node.feedValue;
newNode->levelValue = node.levelValue;
newNode->nameValue = node.nameValue;
newNode->orderValue = node.orderValue;
newNode->preNameValue = node.preNameValue;
Q_ASSERT(q->feedValue == nullptr);
if (q->feedValue != nullptr)
{
qDebug() << "new OriTree build tree error, node Name" << node.nameValue;
return;
}
q->childrenList.insert(node.orderValue, newNode);
}
}
//层次优先遍历多叉树结构(利用队列实现)
void travel( OriTree * tree)
{
if (tree == nullptr)
return;
QQueue<OriTree*> qTree;
qTree.append(tree);
OriTree* p = nullptr;
while (!qTree.isEmpty())
{
p = qTree.front();
qTree.pop_front();
if (p != nullptr)
{
for (int i = 0; i < p->childrenList.count(); i++)
{
qDebug() << p->childrenList.values().at(i)->nameValue;
qTree.append(p->childrenList.values().at(i));
}
}
}
}
//层次深度优先遍历
void travel(OriTree * tree)
{
pathQueue.append(tree);
if (tree == nullptr || tree->childrenList.values().count() == 0)
{
//一条路径遍历完毕,此时pathQueue为完整的节点路径
qDebug() << pathQueue.size();
//将最后入队的节点pop
pathQueue.pop_back();
return;
}
for (int i = 0; i < tree->childrenList.values().count(); i++)
{
BuildTreeItem(tree->childrenList.values().at(i));
if (i == tree->childrenList.values().count() - 1)
{
pathQueue.pop_back(); //当前节点 pop
}
}
}
1.3 哈夫曼树
1.3.1 哈夫曼树定义
哈夫曼树相关的几个名词
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。图 1 中,从根结点到结点 a 之间的通路就是一条路径。
路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。图 1 中从根结点到结点 c 的路径长度为 3。
结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。例如,图 1 中结点 a 的权为 7,结点 b 的权为 5。
结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如,图 1 中结点 b 的带权路径长度为 2 * 5 = 10 。
树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为:
WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3
哈夫曼树定义:
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树”。

1.3.2 哈夫曼树的结构体
//哈夫曼树的结点类型
typedef struct
{
char data;//结点值
double weight;//权重
int parent;//双亲结点
int lchild, rchild;//左右孩子结点
}HTNode;
1.3.2 哈夫曼树构建及哈夫曼编码
哈夫曼树构建
对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法:
1.在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和;
2.在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推;
3.重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树。
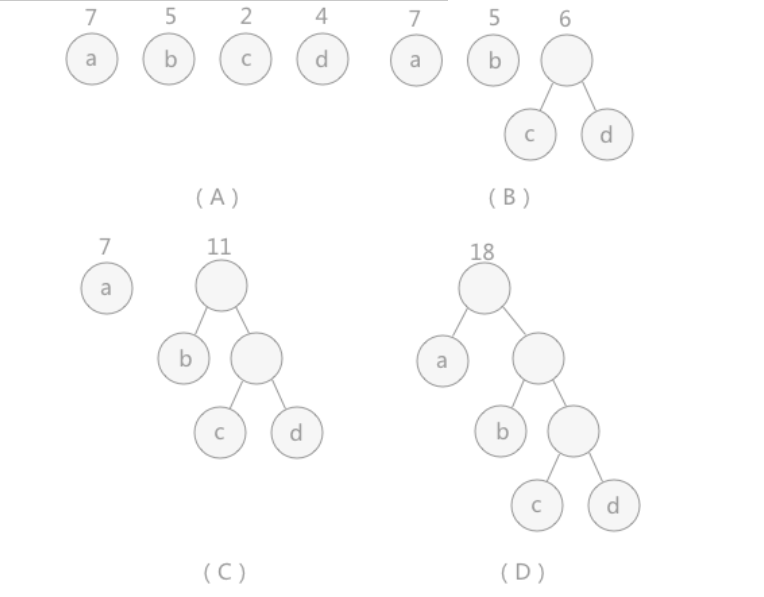
上图中,(A)给定了四个结点a,b,c,d,权值分别为7,5,2,4;第一步如(B)所示,找出现有权值中最小的两个,2 和 4 ,相应的结点 c 和 d 构建一个新的二叉树,树根的权值为 2 + 4 = 6,同时将原有权值中的 2 和 4 删掉,将新的权值 6 加入;进入(C),重复之前的步骤。直到(D)中,所有的结点构建成了一个全新的二叉树,这就是哈夫曼树。
哈夫曼编码
void CreateHuffmanTree(BinaryTree &T, ElemType a[],int n)
{
TNode **Data = new TNode *[n];
for (int i = 0; i < n; i++)
{
TNode *p = new TNode;
p->data = a[i];
p->lchild = NULL;
p->rchild = NULL;
Data[i] = p;
}
for (int i = 0; i < n - 1; i++) //n个结点 需要n-1次循环
{
//每次取两个最小的结点构造哈夫曼树
TNode *p = new TNode;
p->data = Data[0]->data + Data[1]->data;
p->lchild = Data[0];
p->rchild = Data[1];
//删除两个最小结点
for (int i = 2; i < n; i++)
Data[i - 2] = Data[i];
//增加新建的结点
int j = n - i - 2; //j指向未加入哈夫曼树的最大顶点
if (j != 0) //j不等于0 用直接插入排序 插入新建的顶点
{
if (p->data < Data[j]->data)
{
for (j; j >= 0 && p->data < Data[j]->data; j--)
Data[j + 1] = Data[j];
Data[j + 1] = p;
}
else
Data[j] = p;
}
else //j等于0 说明为哈夫曼树的根结点 直接赋值
Data[j] = p;
}
//最后数组里只有一个结点 则哈夫曼树构造完成
T = Data[0];
delete []Data; //释放辅助数组空间
}
void CreateHuffmanCode(BinaryTree T,char *Code[], int n)
{
static int i = 0; //i为编码字符的编号
static int j = 0; //j为每个字符应编码的长度 初试话为0
static char *c = new char[n];
if (T)
{
if (!T->lchild && !T->rchild) //如果为叶子结点 则按照左0右1规则编码
{
c[j++] = '\0'; //结束符
Code[i] = new char[j]; //分配j的长度
strcpy(Code[i++],c); //串复制
j--; //取消结束符
}
if (T->lchild) //左0
{
c[j++] = '0';
CreateHuffmanCode(T->lchild,Code,n);
j--;
}
if(T->rchild) //右1
{
c[j++] = '1';
CreateHuffmanCode(T->rchild,Code,n);
j--;
}
}
delete []c;
}
1.4 并查集
1.4.1.什么是并查集?
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题。常常在使用中以森林来表示。
1.4.2.并查集解决什么问题,优势在哪里?
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中。其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
1.4.33.并查集的结构体、查找、合并操作如何实现?
合并:合并两个集合;
查找:判断两个元素是否为在一个集合
性质:并查集产生的每一个集合都是一棵树
并查集的结构体
typedef struct node
{ int data; //结点对应人的编号
int rank; //结点秩:子树的高度,合并用
int parent; //结点对应双亲下标
} UFSTree; //并查集树的结点类型
初始化并查集
void MAKE_SET(UFSTree t[],int n) //初始化并查集树
{ int i;
for (i=1;i<=n;i++)
{ t[i].data=i; //数据为该人的编号
t[i].rank=0; //秩初始化为0
t[i].parent=i; //双亲初始化指向自已
}
}
并查集的查找
int FIND_SET(UFSTree t[],int x) //在x所在子树中查找集合编号
{ if (x!=t[x].parent) //双亲不是自已
return(FIND_SET(t,t[x].parent)); //递归在双亲中找x
else
return(x); //双亲是自已,返回x
}
并查集的合并
void UNION(UFSTree t[],int x,int y) //将x和y所在的子树合并
{ x=FIND_SET(t,x); //查找x所在分离集合树的编号
y=FIND_SET(t,y); //查找y所在分离集合树的编号
if (t[x].rank>t[y].rank) //y结点的秩小于x结点的秩
t[y].parent=x; //将y连到x结点上,x作为y的双亲结点
else //y结点的秩大于等于x结点的秩
{ t[x].parent=y; //将x连到y结点上,y作为x的双亲结点
if (t[x].rank==t[y].rank) //x和y结点的秩相同
t[y].rank++; //y结点的秩增1
}
}
1.5.谈谈你对树的认识及学习体会。
树更多的需要应用递归思维.
树表示数据表素之间一对多的关系,可以分为二叉树,哈夫曼树等等,遍历的顺序也有很多种:中序遍历,先序遍历、后序遍历、层次遍历等等,分类较多.
树形结构的应用非常广泛
2.PTA实验作业
2.1 二叉树
2.1.1 解题思路及伪代码
BTree CreatTree(string str,int i)
{
定义树的结构变量bt
当i>len-1或str[i]='#'
返回NULL
申请结点BTNode
将str[i]的值赋给bt->data
递归调用函数CreatTree构建左右孩子
返回bt
}
void GetWPL(BTree bt,int h,int &wpl)
{
判断树是否空,如果树为空,返回NULL
如果左右孩子均不为空
wpl+=bt->data-'0'乘以所在层数
递归调用函数GetWpl,其中的h+1,得到所在层数
}
2.1.2 总结解题所用的知识点
1)建立二叉树
2)调用递归
2.2 目录树7-7 目录树
2.2.1 解题思路及伪代码
解题思路:首先建立孩子兄弟链的结构,读入字符串并分离,判断是文件还是目录,分别进入各自的函数,文件函数通过对比优先级的高低,若高则改变指针的位置原来位置变为其孩子,低则作为孩子插入,相同则在其当前位置基础上进行操作,目录函数则是对兄弟链进行操作。
伪代码:
while (str.size() > 0)
{
查找字符串中是否有’\’,并记录下位置pos
if (没有)
说明是文件,则进入插入文件的函数
else
说明是目录,则进入插入目录的函数里
bt要跳到下一个目录的第一个子目录
while (bt!NULL&&bt->name != name)
bt = bt->Brother;//找到刚刚插入的目录,然后下一步开始建立它的子目录
将刚插进去的目录从字符串中去掉
}
//插入文件操作
if(情况1:bt为空,情况2:当前为文件,且优先级大于当前结点)
{
新建结点将原结点作为其兄弟;
}
if(相同)
{
返回;
}
作为兄弟插入;
//插入目录操作
转移目录位置
if(情况1:目录为空 情况2:当前结点为文件 情况3:优先级大)
{
新建结点原结点作为其兄弟;
}
if(相同)
{
返回;
}
作为兄弟插入;
2.2.2 总结解题所用的知识点
利用孩子兄弟链结构进行存储,比较优先级插入结点并且改变结点位置,以及先序和后序遍历方式,递归函数调用计算高度。
3.阅读代码
3.1 题目及解题代码

代码:
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ans;
if (!root) {
return ans;
}
queue<TreeNode*> nodeQueue;
nodeQueue.push(root);
bool isOrderLeft = true;
while (!nodeQueue.empty()) {
deque<int> levelList;
int size = nodeQueue.size();
for (int i = 0; i < size; ++i) {
auto node = nodeQueue.front();
nodeQueue.pop();
if (isOrderLeft) {
levelList.push_back(node->val);
} else {
levelList.push_front(node->val);
}
if (node->left) {
nodeQueue.push(node->left);
}
if (node->right) {
nodeQueue.push(node->right);
}
}
ans.emplace_back(vector<int>{levelList.begin(), levelList.end()});
isOrderLeft = !isOrderLeft;
}
return ans;
}
};
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/binary-tree-zigzag-level-order-traversal/solution/er-cha-shu-de-ju-chi-xing-ceng-xu-bian-l-qsun/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3.2 该题的设计思路及伪代码
此题是「102. 二叉树的层序遍历」的变种,最后输出的要求有所变化,要求我们按层数的奇偶来决定每一层的输出顺序。规定二叉树的根节点为第 00 层,如果当前层数是偶数,从左至右输出当前层的节点值,否则,从右至左输出当前层的节点值。
我们依然可以沿用第 102 题的思想,修改广度优先搜索,对树进行逐层遍历,用队列维护当前层的所有元素,当队列不为空的时候,求得当前队列的长度 \textit{size}size,每次从队列中取出 \textit{size}size 个元素进行拓展,然后进行下一次迭代。
为了满足题目要求的返回值为「先从左往右,再从右往左」交替输出的锯齿形,我们可以利用「双端队列」的数据结构来维护当前层节点值输出的顺序。
双端队列是一个可以在队列任意一端插入元素的队列。在广度优先搜索遍历当前层节点拓展下一层节点的时候我们仍然从左往右按顺序拓展,但是对当前层节点的存储我们维护一个变量 \textit{isOrderLeft}isOrderLeft 记录是从左至右还是从右至左的:
如果从左至右,我们每次将被遍历到的元素插入至双端队列的末尾。
如果从右至左,我们每次将被遍历到的元素插入至双端队列的头部。
当遍历结束的时候我们就得到了答案数组。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号