【朱刘算法】最小树形图

最小树形图

1 DAG的最小树形图

一个树形图中，除了r点其他点都只有一个入边

那么对于一个DAG，只要我们对于每一个点选出最小的入边，那么这一定是个树形图

那么算法就非常的简单

2 环的最小树形图

这个问题十分傻，显然，从r开始绕一圈少一条边就行了

3 真正的最小树形图

这个东西叫做朱刘算法。

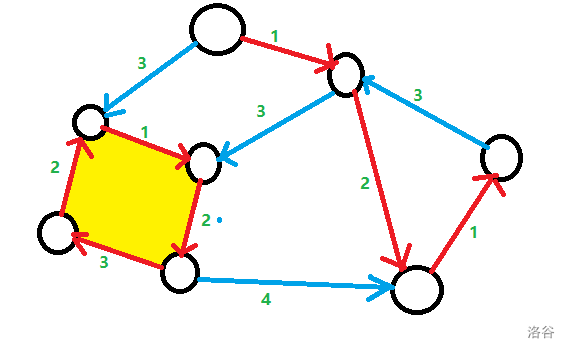
1）建图原理

先用DAG的算法找出每个点的最小入边记为红边，其他边记为蓝边。黄色部分是红边形成的环。

如果黄色的环不存在，则我们直接得到了最小树形图，直接输出。

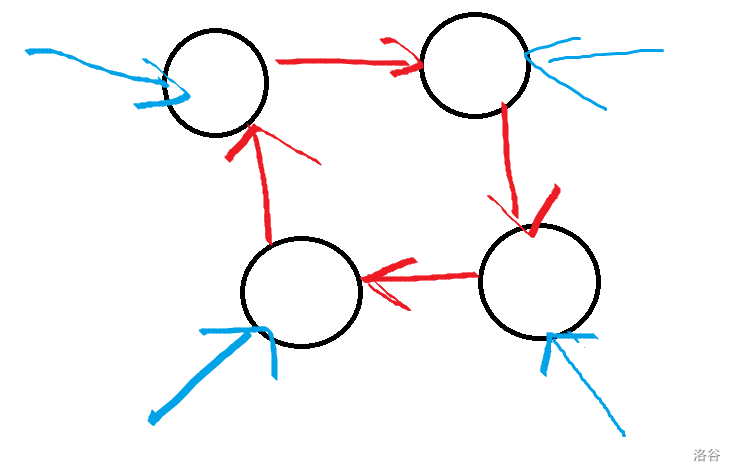
那么如果是上面这种情况。如果存在环，那么这个环内的点不会被外部的点连接，因为每个点只有一个入度，全被环内占据了。

而我们要得到最小树形图，就需要把其中一条边换成环外边。

将环缩成一个点，环外边指向该点。

为了方便统计，由于我们确信环外边的长度 \(\ge\) 环内边的长度，那么我们ans先加上这个环的边权和，然后每一条环外边 \(E_u\) ，其权值 \(val_u=val_u-val_{nei}\) ,其中 \(E_{nei}\) 是该点的最小入边。

用那张图解释一下：

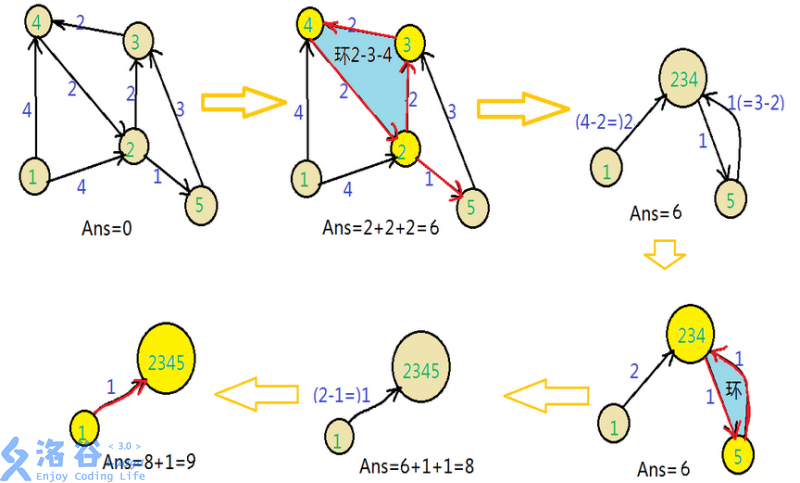(引用一下别人的别人的别人的题解的图，这张图实在太好用了，放这里做参考)

这样有什么好处？

这样相当于进行本质不变的图形转化，使得我们可以把环缩成一个点。环上的边相当于占据了外部边的部分边权，将这个边权从外部边上减去，此时环再与外部边相连，就等同于舍弃了环内一边，连上环外一边，而答案就只需要加上外部边剩下的边权。同时，这样环本质上就变成了一个独立的点，将原图刷新后得到一张新的图，和原图本质不变，但减少了环。就这样不断地用新图重复上述找环操作，最后的图一定是DAG，得到的答案即为DAG的答案。

2）如何找环

对于一个点 \(u\) ,设其红色入边的出发点为 \(fa[u]\) 。

再设 \(u\) 最早的祖宗（\(u\) 的最早前驱) 为 \(tp[u]\) 。

遍历每个 \(u\) ，然后让 \(u\) 沿着 \(fa\) 逆向走边，直到根或者前驱是自己的点。

1.如果走到根，那么这个点不在环上；

2.如果 \(u\) 走到了某个 \(v\), 使得 \(tp[v]==u\) ,那么 \(v\) 就是一个环上的点。

为方便，设 \(lp[u]\) 表示 \(u\) 所属的环，若 其为0，代表该点还没有所属的环，设置新环 \(lp[u]=++cnt\) ,环上每个点都要标记。

for(int u=1,v=1;u<=n;u++,v=u)
{
    while(v!=root &&tp[v]!=u && !lp[v])
    {
        tp[v]=u, v=fa[v];//v是u向上逆行的fa
    }//退出循环代表 tp[v]==u，u的祖先的前驱是u，那就形成了环
    if(v!=root && ！lp[v])
    {
        lp[v]=++cnt;
        for(int k=fa[v];k!=v;k=fa[k]) lp[k]=cnt;
    }//环上每个点打标记
}

3）何时结束

一但没有环，就是最小树形图。

4）实际操作

每一个循环中，找到每个点的红边，再判断是否成环，将环的外部边边权刷新，最后把环当点建新图，重复循环直到没有环存在

算法流程

对每一次循环：

(1).贪心找红边，记录入边的起点（父亲）

(2).把所有红边加入ans，若一点没有红边，则图不连通，输出false

(3).找环

(4).没有环，直接退出

(5).所有不是环的点设为大小为1的独立环

(6).原先的图转化为现在缩点的图

(7).对新图重复以上操作

代码:

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=107,maxm=1e4+7;
int n,m,ans,root;
int fa[maxn],tp[maxn],lp[maxn],mn[maxn];
int cnt=0;
struct edge{
    int u,v,w;
}e[maxm];


int zl()//朱刘算法
{
    while(true)
    {
        cnt=0;
        for(int i=1;i<=n;++i) mn[i]=1e9,fa[i]=tp[i]=lp[i]=0;
        //初始化
        for(int i=1,v,w;i<=m;++i)//(1)
            if(e[i].u!=e[i].v && (w=e[i].w)<mn[v=e[i].v])
            {
                mn[v]=w; fa[v]=e[i].u;
            }//遍历所有边,找红边
        mn[root]=0;
        
        for(int u=1;u<=n;++u)//(2)
        {
            ans+=mn[u];
            if(mn[u]==1e9) return -1;//图不连通，输出false
        }
        
        for(int u=1,v=1;u<=n;++u,v=u)//(3)
        {
            while(v!=root && tp[v]!=u && !lp[v])
            {//根节点没有入边，所以root不可能成环
                tp[v]=u; v=fa[v];
            }
            if(v!=root && !lp[v])
            {
                lp[v]=++cnt;
                for(int k=fa[v];k!=v;k=fa[k])
                {
                    lp[k]=cnt;
                }
            }
        }
        
        if(!cnt) return ans;//(4)没有环了，输出答案
        
        for(int u=1;u<=n;++u) if(!lp[u]) lp[u]=++cnt;//(5)
        
        for(int i=1;i<=m;++i)//(6)
        {
            e[i].w -= mn[e[i].v];//所有红边都计入答案，外部点改边权去重
            e[i].u = lp[e[i].u];//原边关系转化为缩点后环的关系
            e[i].v = lp[e[i].v];//同上,建新图
        }
        n=cnt, root = lp[root];//新图的n和根
    }//(7)
}
int main(){
	scanf("%d%d%d",&n,&m,&root);
	for(int i=1,u,v,w;i<=m;i++)
		scanf("%d%d%d",&u,&v,&w),e[i]=(edge){u,v,w};
	printf("%d",zl());
	return 0;
}

极致简约版

#include<iostream>
using namespace std;
enum{maxn=107,maxm=10007};
int n,m,ans,root,fa[maxn],tp[maxn],lp[maxn],mn[maxn],cnt;
struct edge{int u,v,w;}e[maxm];
int zl(){      
        for(;true;) {
        for(int i=1;i<=n;++i) mn[i]=1e9,fa[i]=tp[i]=lp[i]=0;
        for(int i=1,v,w;i<=m;++i)
            if(e[i].u!=e[i].v && (w=e[i].w)<mn[v=e[i].v])  mn[v]=w,fa[v]=e[i].u;
        mn[root]=0;
        for(int u=1;u<=n;++u) {ans+=mn[u]; if(mn[u]==1e9) return -1;}
        for(int u=1,v=1;u<=n;++u,v=u){
            while(v!=root && tp[v]!=u && !lp[v]) {tp[v]=u,v=fa[v];}
            if(v!=root && !lp[v]) { lp[v]=++cnt; for(int k=fa[v];k!=v;k=fa[k]) lp[k]=cnt;}
        }
        if(!cnt) return ans;
        for(int u=1;u<=n;++u) if(!lp[u]) lp[u]=++cnt; 
        for(int i=1;i<=m;++i) {e[i].w -= mn[e[i].v],e[i].u = lp[e[i].u],e[i].v = lp[e[i].v];}
        n=cnt,root=lp[root],cnt=0;
    }
}
int main(){ios::sync_with_stdio(0);cin>>n>>m>>root;
	for(int i=1,u,v,w;i<=m;i++) cin>>u>>v>>w,e[i]=(edge){u,v,w};
	return cout<<zl(),0;
}