那就从k-means开始吧
对于机器学习的新手小白来说,k-means算法应该都会接触到吧。传统的k-means算法是一个硬聚类(因为要指定k这个参数啦)算法。这里利用百度的解释
它是数据点到原型的某种距离作为优化的目标函数,利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度,它是求对应某一初始聚类中心向量V最优分类,使得评价指标J最小。算法采用误差平方和准则函数作为聚类准则函数。
看上去好难懂,实际上任务就是要聚类,然后将相关的点聚成一堆嘛。这里我们可以给出k-means的核心公式
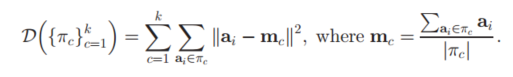
这里可以看到,实际上就是计算每个样本点簇中心的距离,然后判断出到哪个簇中心距离最短,然后分给那个簇。然后下次迭代时,簇中心就按照新分配的点重新进行计算了,然后所有的点再同样计算样本点到簇中心的距离,重新分配到不同的簇中。所以这样不断迭代下去,就能够收敛了,得到最后的聚类效果。
加上“核”?那就成了Kernel k-means
“核”是什么
核函数的方法已经被提出很久了,也得到了很多的推广应用。很多算法参进了核函数,就变得有趣得多。核函数通常与SVM经常结合在一起进行使用。总的来说,核函数,就是将输入空间,映射到高维的特征空间。然后再在高维的数据同看进行数据处理。这种映射的话,是非线性变换的,这也才能能够将输入空间映射出不同特征的高维空间。
当然,要给出这种非线性运算的确切算法,是很困难的。所以当我们的现实运算算法求解时候只用到了样本点的内积运算时候,而在低维输入空间中,我们有能够得到某个函数K(x,x′),它恰好等于在高维空间中这个内积,即K( x, x′) =<φ( x) ⋅φ( x′) > 。
那么这样就好办了,只要我们每次计算样本点投射到高维空间的值进行内积运算时,我们直接只需要使用函数K(x,x′),就可以得到。这就避免了我们将样本点映射到高维空间的操作,减少了计算的难度和复杂度。所以每次进行运算,只需要运算K(x,x′)即可。(理解这一点很重要噢,为下面Kernel k-means做铺垫)
那就给 k-means 加个“核”吧
核k-means,概括地来说,就是将数据点都投影到了一个高维的特征空间中(为啥要这么做呢,主要是突显出不同样本中的差异),然后再在这个高维的特征空间中,进行传统的k-means聚类。主要的思想就是这么简单,比起传统普通的k-means就多了一个步核函数的操作。所以它的公式也与传统k-means很相近:

这里所表示的,$a_i$是各个样本点,而$\phi( )$函数,则是表示将样本点映射至高维空间。而公式中的$m_c$,则是每个簇中的质心。
这个形式,对比起普通的k-means是不是很相近咧,同样是求各个高维空间中的样本特征(传统k-means中是样本点)与质心的距离,然后根据该样本点到不同质心距离,选择最小的(也就是说距离该样本点最近)的簇心,进行分配(将该样本点归为这个簇)。
这就让我们想起普通k-means的计算了,先算出各个簇具体簇心的具体值,然后就对所有样本点重新计算到各个簇心的距离,然后进行重新分派。
然而,在kernel k-means中,计算方法普通k-means大有不同。首先,在上述的公式中,$\phi(a_i)$,这个我们是很难算出来的。因为之前说明核函数的时候提到,这个这种非线性的函数映射,我们很难去得到准确的函数算法;其次,对于每个簇的中心$m_c$,即使我们有簇内所有点的数据,但我们也还是是很难去准确描述这个中心的。
因此,我们要开始对这个公式进行改造啦。
首选,我们将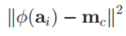
改写成

这个变化很明显是将这个平方公式进行展开,然后对$m_c$进行了替换,因为$m_c$实际上就是簇内所有数据所决定的。但是我们难以准确去表示而已,但是我们在算法等价上,这样运算的结果还是与质心相同的。
所以我们最终要计算的公式也发生了变化。将原本的完全平方式,进行了展开。
观察上面的完全平方展开式,我们可以发现:每一项中,需要使用到高维特征空间的值,都是在进行内积运算。因此符合我们之前所提到的,使用一个矩阵K函数,来代表高维特征空间中这两个值的内积结果。
即$k<a_i,a_j>$等价于$\phi(a_j)\phi(a_i)$。这样子,我们就根本不用管$\phi()$这个函数实际的运算定义是怎样的了。只需要使用到这两个特征进行相乘的结果。
来个小结
kernel k-means实际上公式上,就是将每个样本进行一个投射到高维空间的处理,然后再将处理后的数据使用普通的k-means算法思想进行聚类。
在计算上的话,由于要映射到高维空间中,而且还要找出各个簇的中心。这些如果没有能够得到映射到高维空间的函数,是很难直接计算到的。但是我们可以观察到,我们所要计算的公式,最终并不需要知道单独的一个样本点映射到高维空间的特征值,而是两个高维空间特征值的内积。所以,我们只需要得到一个K矩阵,矩阵中每个元素都表示高维空间,这两个样本点映射成特征后,进行内积计算所得到的结果。所以这个矩阵,实际上就是一个核函数矩阵。
那就再加上权重w来个weighted kernel k-means吧
看到这里,应该起码对kernel k-means有个理解吧。然后我们还要在这个基础,再加上一个权重w,也就是对每一个样本点,都给出一个权重$w_j$,区分出不同样本点的重要性。所以的话,我们的公式又增添了一点东西:

这里可以看到,公式中计算样本高维空间特征到簇中心距离 的平方后,还乘以了一个权重$w_j$,对于不同的样本点,其权重都可能不同。所以就只是简单地乘多了一个权重,公式的计算方法跟 kernel k-means还是很相似的。
我们将平方项展开,然后将$m_c$项进行替换。然后我们的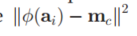
得到以下结果:
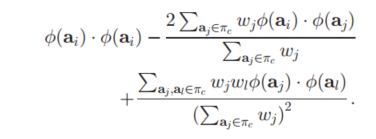
如果我们再将其中的$\phi(a_i)\phi(a_i)$使用K的核函数矩阵($K(a_i,a_j)=phi(a_i)\phi(a_i)$)进行替换,则得到以下结果:
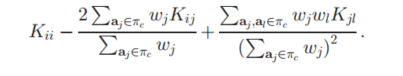
简直完美,是吧。
下篇预告
时间比较紧,所以就先写这些,关于算法的实现细节,以及复杂度分析。将于下篇介绍。
算法代码已经推上了码云,有兴趣的小伙伴可以clone下来把玩。
https://git.oschina.net/subaiDeng/Kernel-k-means
另外,写这篇博客,是参考了正在查阅的一篇论文:
《Weighted Graph Cuts without Eigenvectors : A Multilevel Approach》
Yuqiang Guan and Brian Kulis
大家有兴趣也可以去看看。
花絮
本人学浅才疏,若在书写内容或者表达方式上存在错误,欢迎大家指出,也欢迎大家一起讨论。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号