算法笔记之N叉树的最大深度(用队列、栈和递归实现)

559. N 叉树的最大深度 原题链接

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：

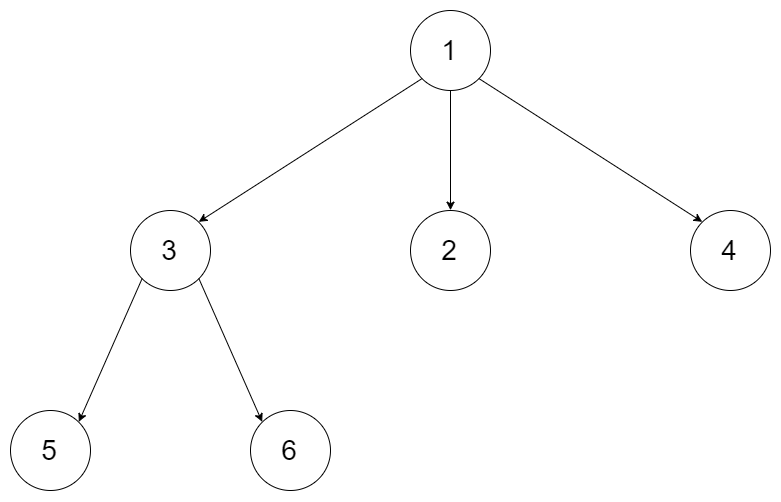
输入：root = [1,null,3,2,4,null,5,6]
输出：3

解题

这个跟求二叉树的最大深度相似，不过是子节点数变成了N。求解的时候可以参考层序遍历用队列实现，比较好理解。也可以用栈实现的后序遍历，但觉得不太好理解。

1. 用队列

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""
import collections
class Solution: 
    def maxDepth(self, root: 'Node') -> int:
        if root is None:
            return 0
        que = collections.deque() # 定义一个队列
        que.append(root)  # 把根节点添加至队列
        depth = 0
        while que: # 迭代处理，直到队列为空
            size = len(que) # 每次处理一层
            depth += 1  # 深度+1
            for i in range(size):  # 处理一层的所有节点
                node = que.popleft() # 从左到右取该层的一个节点
                if node.children:  # 把该节点的所有子节点加入队列。所有这些子节点属于同一层。计算完毕后进入下一个while循环。
                    for j in range(len(node.children)):
                        que.append(node.children[j])
        return depth

2. 栈
   这里采用的后序遍历。

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""
import collections
class Solution: 
    def maxDepth(self, root: 'Node') -> int:
        
        stack = []
        depth = 0
        tmp = 0
        
        if root:
            stack.append(root)
        while stack:
            node = stack.pop()
            if node:  # 节点不为空，重新入栈，但是在后面添加一个空节点，标记一下该节点的子节点已经做过了处理
                tmp += 1  # 当还有节点时，tmp会一直增加，直到到达最下面一层
                stack.append(node)  # 重新入栈
                stack.append(None) # 添加一个空节点作为标记
                if node.children:  # 所有子节点入栈
                    for i in range(len(node.children)):
                        stack.append(node.children[i])
            else:  # 节点为空，说明下一个节点被标记为了不作处理，直接跳过
                stack.pop()
                tmp -= 1  
            depth = max(depth,tmp)
        return depth 

3. 递归

class Solution: 
    def maxDepth(self, root: 'Node') -> int:
        if root is None:
            return 0
        depth = 0
        for i in range(len(root.children)):
            depth = max(depth, self.maxDepth(root.children[i]))
        return depth + 1
'''
如果是二叉树，因为最多只有2个子节点，可以省去for循环，直接返回左右子树的最大深度即可 
return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))
'''