笔记第一节 机器学习基本概念简介

一、Machine Learning

1.What is Machine Learning

机器学习用一句话概括，就是让机器具有找函式能力，用这个函式来实现目标。
如机器做语音辨识,机器听一段声音,输入是声音讯号,输出是这段声音讯号的内容。这个函式他非常非常的复杂,人类绝对没有能力把它写出来,所以凭机器力量,把这个函式自动找出来，这件事情,就是机器学习。
如影像辨识输入是一张图片,输出是图片内容。
如下围棋，输入是棋盘现状，通过函式，机器能够输出下一步要下位置。

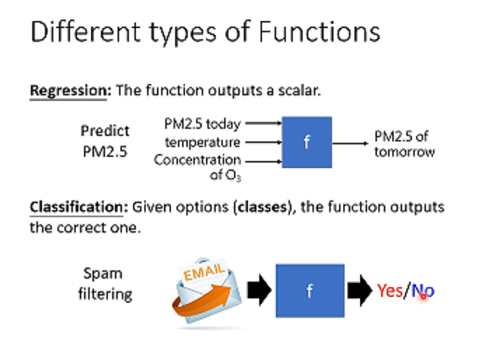
2.Different types of Functions

Regression：机器函式输出是一个数值，是一个scalar。
Classification：要机器做的是选择题。先准备好一些选项，选项又叫作类别（classes）,从设定好选项里面选择一个当作输出。
Structured Learning：要叫机器学会创造这件事情。

3.Find the fuction

（1）写出Model

第一步写出Function with Unknown Parameters。
最初步的猜测,我们写成y=b+w*x。y是要预测的东西。x是已知条件，称为Feature。b跟w是未知参数，跟Feature做相乘的未知参数w，称为weight，与Feature相加未知参数，称为Bias。未知参数往往需要猜测，这个猜测往往就来自对这个问题本质上的了解，也就是Domain knowledge。
Model在机器学习里是一个带有未知Parameter的Function。

（2）定义Loss

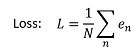
Loss也是一个Function,那这个Function输入是Model里面参数。这个Function输出值代表,这一组未知参数设定某一个数值时,这组数值对于Model好坏程度。
Loss越大,代表我们现在这一组参数越不好;Loss越小,代表现在这一组参数越好。

（3）Optimization

第三步要做事情是解一个最佳化问题。
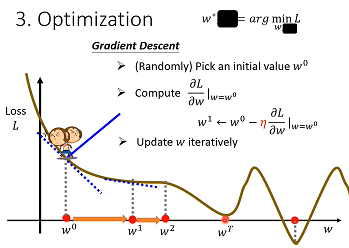
我们用到Optimization方法是Gradient Descent（梯度下降法）。
首先，随机选取一个初始点w₀,那这个初始点往往是随机,那在往后课程也许有一些方法,我们先当作都是随机的,那假设我们随机决定的结果,是在w₀这个地方。
那接下来，计算在w等于w0时候,w这个参数对loss微分,计算在w₀这个位置error surface切线斜率,也就是图上蓝色虚线,它的斜率,那如果斜率是负代表在这个位置附近,左边比较高右边比较低,把w值变大就可以把loss变小。如果算出来的斜率是正的,就代表说左边比较低右边比较高,那就代表我们把w变小了,可以让Loss值变小,那这个时候你就应该把w的值变小。
w移动一步大小取决于两件事情：斜率大小和学习速率learning rate。这个地方斜率大,这个步伐就跨大一点,斜率小步伐就跨小一点。学习率是自己设定,如果η大一点,那每次参数update就会量大,学习可能就比较快。这种你在做机器学习,需要自己设定的东西,叫做hyperparameters。
停下来：次数上限和微分值为0。

多个参数时，按同样方法进行计算。

4.Linear model

把feature乘上一个weight,再加上一个bias就得到预测的结果,这样的模型有一个共同的名字叫做Linear model。
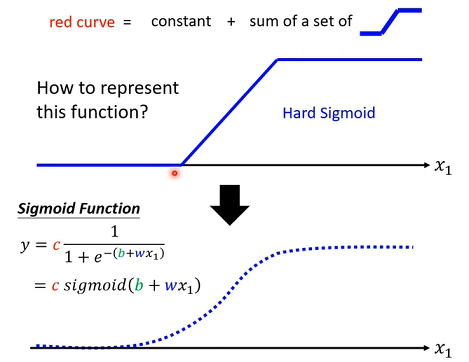
Piecewise Linear curves=constant+sum of a set of Hard Sigmoid

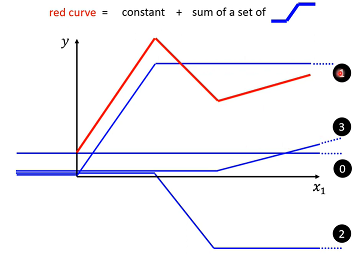
可以用 Piecewise Linear Curves逼近任何连续曲线,而每一个Piecewise Linear Curves又可以用一些蓝色Function组合起来,也就是说只要有足够蓝色Function把它加起来,就可以变成任何连续曲线。
对于这个蓝色Fuction表示，通常用一个 Sigmoid Function,来逼近这一个蓝色Function。 Sigmoid Function 就是S型Function,因为长得有点像S型,所以叫它Sigmoid Function。这个蓝色Function就叫做,Hard的Sigmoid。

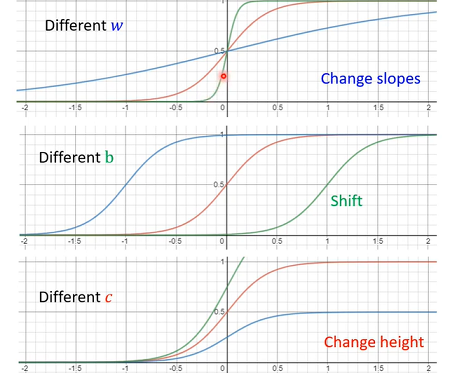
w改变斜率。b改变左右移动。c改变高度。不同w不同b不同c,就有不同Sigmoid Function,把不同Sigmoid Function叠起来以后,可以去逼近各种不同Piecewise Linear Function,进一步拿来近似各种不同Continuous Function。

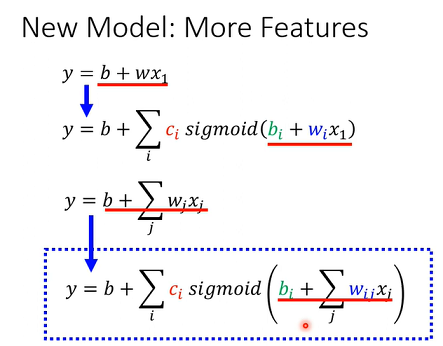
其实有办法写出一个非常有弹性有未知参数Function,就是Summation一堆Sigmoid,但它们有不同c不同b不同w。进化到不是只用一个Feature,可以用多个Feature。

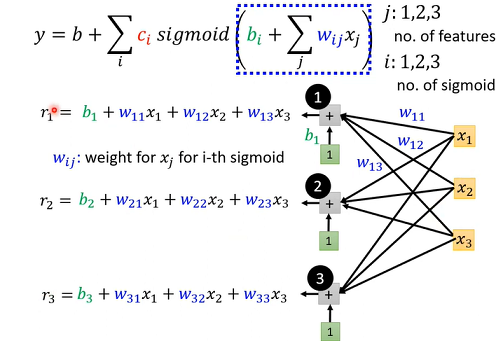
先考虑一下j是 1 2 3 状况,就是只考虑三个Feature。
用w_{ij}来代表在第i个Sigmoid乘给第j个Feature的Weight。第一个Feature是乘w11,第二个Features是乘w12,第三个Feature是乘w13,所以有三个Sigmoid Function。
简化起见,把括号里数字,用一个简单符号来表示ri。

计算可以表示为下图形式。

改成线性代数常用表示方式,x乘上矩阵w再加上向量b,会得到一个向量叫做r。在这个括号就是x乘上w加上b等于r,r分别通过Sigmoid Function得到a。这个蓝色虚线框就是从x1 x2 x3得到了a1 a2 a3。
接下来这个Sigmoid输出还要乘上ci然后还要再加上b。这个c称为Transpose。a乘上c的Transpose再加上b就得到了y。
整体而言，是输入x,Feature是x,x乘上矩阵w加上向量b得到向量r。再把向量r透过Sigmoid Function得到向量a,再把向量a跟乘上c的Transpose加上b就得到y。

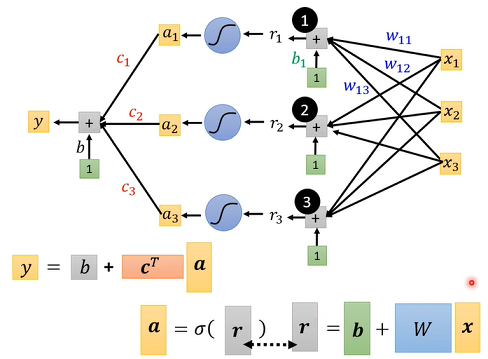
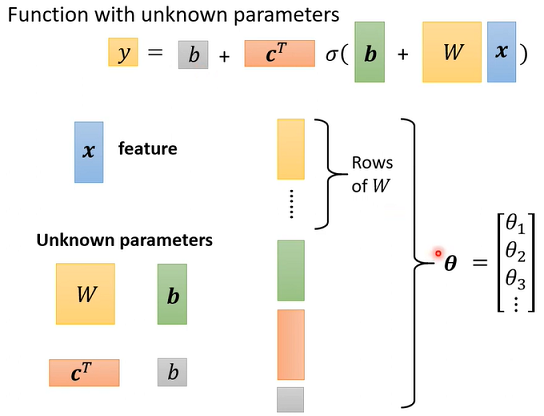
黄色b是一个向量，灰色b是一个数值，这两个不一样。把未知参数拉出来组成一个向量，直接用一个符号θ表示。

5.Back to ML_Step 2 :define loss from training data

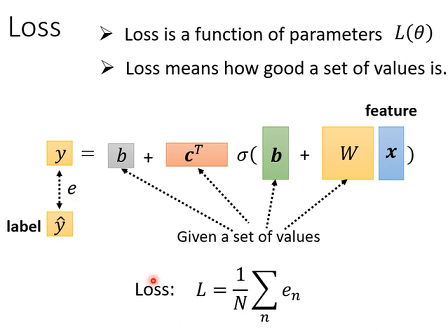
有了新Model以后,Loss没有什么不同,定义方法是一样,只是未知参数很多，直接用θ来统设所有参数,所以我们现在的 Loss Function 就变成L(θ)。计算方法和之前一样。
先给定某一组θ,然后把一种Feature带进去,然后计算一下y跟真实Label 之间差距e，把所有的误差通通加起来得到Loss。

6.Back to ML_Step 3: Optimization

Optimization跟前面提到步骤一样。

现在θ是一个很长向量,把它表示成θ1 θ2 θ3等。找一组 θ,这个θ可以让Loss越小越好。
第一步，随机选一个初始数值θ0。
第二步，对每一个未知参数,这边用θ1 θ2 θ3来表示,每一个未知的参数计算它对L微分，集合起来它就是一个向量,那个向量我们用g（Gradient）来表示。在L前面放了一个倒三角形代表Gradient,意思就是,把所有参数θ1 θ2 θ3都拿去对L作微分。括号里θ0意思是算微分位置是在θ等于θ0位置。
第三步，更新参数方法和之前一样。θ_1^{0减掉η乘上微分值,得到θ_1}1,代表θ1更新过一次结果。以此类推。由θ0算Gradient,根据Gradient把θ0更新成θ1,然后再算一次Gradient根据 Gradient把θ1再更新成θ2,再算一次Gradient把θ2更新成θ3。直到设定次数或者Gradient是0向量。