OO第三单元总结
在第三单元中,我们接触了契约式编程,学习了JML的语法,感受到了它的优点和不足。这一单元的作业与以往两个单元完全不同,我们不再是从零开始编写程序,而要根据给定的JML实现特定接口,使得程序能够正确运行。很明显,这种编程方式更加贴近当下工业界的开发过程。
一、利用JML准备数据
得益于契约式编程,我们在测试第三单元的作业时不必考虑程序整体的运行,只需要保证每个被实现的方法都能够严格按照JML规格执行即可。因此,这一单元的作业十分适合单元测试(对程序最小的可测试单元进行检查和验证)。
接下来的问题就是如何构造单元测试的程序呢?既然只需要测试方法是否满足JML的需要,那么就可以通过JML来构造测试数据。那么如何判断构造的数据的质量呢?我认为数据最重要的指标是覆盖率。
代码中如果出现if-else, while 等语句,就会产生新的分支,分支越多,程序越复杂。程序的复杂度可以用圈复杂度来衡量。
我们理想中的数据集要能够覆盖所有的分支。要注意的是,这里所指的分支是JML的分支,而不是具体实现的方法的分支。因为,一般情况下JML的分支数要比具体实现少,测试起来工作量小。并且测试JML的每个分支就可以保证正确性。
以下面这段JML为例:
/*@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < groups.length; groups[i].getId() == id2) &&
@ (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1) &&
@ getGroup(id2).hasPerson(getPerson(id1)) == false &&
@ getGroup(id2).people.length < 1111;
@ assignable getGroup(id2).people;
@ ensures (\forall Person i; \old(getGroup(id2).hasPerson(i));
@ getGroup(id2).hasPerson(i));
@ ensures \old(getGroup(id2).people.length) == getGroup(id2).people.length - 1;
@ ensures getGroup(id2).hasPerson(getPerson(id1));
@ also
@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < groups.length; groups[i].getId() == id2) &&
@ (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1) &&
@ getGroup(id2).hasPerson(getPerson(id1)) == false &&
@ getGroup(id2).people.length >= 1111;
@ assignable \nothing;
@ also
@ public exceptional_behavior
@ signals (GroupIdNotFoundException e) !(\exists int i; 0 <= i && i < groups.length;
@ groups[i].getId() == id2);
@ signals (PersonIdNotFoundException e) (\exists int i; 0 <= i && i < groups.length;
@ groups[i].getId() == id2) && !(\exists int i; 0 <= i && i < people.length;
@ people[i].getId() == id1);
@ signals (EqualPersonIdException e) (\exists int i; 0 <= i && i < groups.length;
@ groups[i].getId() == id2) && (\exists int i; 0 <= i && i < people.length;
@ people[i].getId() == id1) && getGroup(id2).hasPerson(getPerson(id1));
@*/
可以看到它一共有三个分支:两个normal_behavior和一个exceptional_behavior。对于每一个分支构造满足requires语句条件的数据,然后检查输出是否符合ensures语句。
二、本单元架构设计
第一次作业
第一次作业主要的任务是完成在Network中添加Person和Group的对象,并且支持Person对象之间建立关系,还要能够查询两个人之间是否存在间接关系。
分析需求,我们发现主要有两个问题:
-
建立Network/Person/Group中基本的数据结构
-
根据Person之间的关系建图,支持并查集的查询
第一个问题,我用HashMap作为基本的数据结构来存储数据,并且根据接口参数类型不同,在三个类中采用了不同的Key——Value组合。
在MyNetwork类中,多用id查找Person,所以Key为id,Value为Person
public class MyNetwork implements Network {
private final HashMap<Integer, Person> people; //id to person
private final HashSet<Group> groups;
private int blockCount;
}
在MyPerson类中,每个Person对应一个value,所以Key为Person,Value为value
public class MyPerson implements Person {
private final int id;
private final String name;
private final int age;
private MyPerson root;
private final HashMap<Person, Integer> acquaintance;
}
在MyGroup类中,并不需要查找特定的Person,所以直接用HashSet
public class MyGroup implements Group {
private final int id;
private final HashSet<Person> people;
}
第二个问题,并查集并不需要建图,只需要在添加边的时候查找两个点所属的联通块的根节点再合并即可。考虑封装性,可以直接在MyPerson里实现查找根节点
public static MyPerson findRoot(MyPerson person) {
if (person.root == person) {
return person;
} else {
person.root = findRoot(person.root);
return person.root;
}
}
第二次作业
第二次作业增加了一个新接口Message和新方法queryLeastConnection,后者是求网络中某个点所在连通块的最小生成树。Message在本次作业中不是难点,按照之前设计MyNetwork/MyPerson/MyGroup的思路设计即可。主要的难点是求最小生成树。
由于最小生成树需要遍历边集,所以必须记录下来所有的关系。我新声明了一个类Edge,用来保存边,并且实现了Comparable接口,便于排序。
public class Edge implements Comparable<Edge> {
private final int id1;
private final int id2;
private final int value;
public Edge(int id1, int id2, int value) {
this.id1 = id1;
this.id2 = id2;
this.value = value;
}
由于最小生成树还需要使用并查集算法,所以必须再维护一个“节点——节点所在连通块的祖先”的关系。在第一次作业中,我把并查集集成在了MyPerson类里面,为了不导致混乱,这次我在MyNetwork中使用一个HashMap来维护连通块,这是一个id => id的映射。
private final HashMap<Integer, Integer> father;
第三次作业
第三次作业对第二次作业引入的Message接口进行了完善,引入了多个继承Message接口的接口。除此之外,还要实现计算单源最短路的功能。对于新增加的接口一一实现,根据其要求修改之前的一些方法,并不涉及架构的改动。而主要影响架构的是单源最短路的计算。
为了能够使用堆优化的dijkstra,我们需要定义新的类Point,它代表一个图上的节点,记录的信息是起点到这个节点的距离和这个节点的id。为了能够使用优先队列,Point类继承Comparable接口,按距离从小到大排序。
public class Point implements Comparable<Point> {
private int dist;
private final int id;
public Point(int dist, int id) {
this.dist = dist;
this.id = id;
}
三、性能问题和修复情况
第一次作业
第一次作业的性能问题主要在并查集,但其实并查集算法并不难实现,而真正的难点在于看懂JML。
例如queryBlockSum方法,需要思考得很深入才能发现其实答案等价于连通块个数。
/*@ ensures \result ==
@ (\sum int i; 0 <= i && i < people.length &&
@ (\forall int j; 0 <= j && j < i; !isCircle(people[i].getId(), people[j].getId()));
@ 1);
@*/
public /*@ pure @*/ int queryBlockSum();
第二次作业
第二次作业的性能问题在于最小生成树,最小生成树有两种算法,prim和kruskal。设边数为m,点数为n,那么prim的复杂度是O(n^2),kruskal的复杂度是O(mlogm),不难发现本次的数据规模kruskal更合适。
此外,有一个容易被忽视的方法,它的复杂度很高,高达O(n^3),就是Group中的getValueSum
/*@ ensures \result == (\sum int i; 0 <= i && i < people.length;
@ (\sum int j; 0 <= j && j < people.length &&
@ people[i].isLinked(people[j]); people[i].queryValue(people[j])));
@*/
public /*@ pure @*/ int getValueSum();
如果直接按照JML一板一眼来写的话,复杂度高达O(n^3)。不过,不难发现,只要对每个group维护一个valueSum,然后每次addRelation的时候遍历所有group,更新valueSum。这样复杂度就变成均摊O(n)了。
第三次作业
第三次作业的性能问题在于单源最短路,由于我们的社交网络是非负权图,所以直接使用堆优化的dijkstra来实现。
四、Network扩展
扩展的四个类的uml图如下:
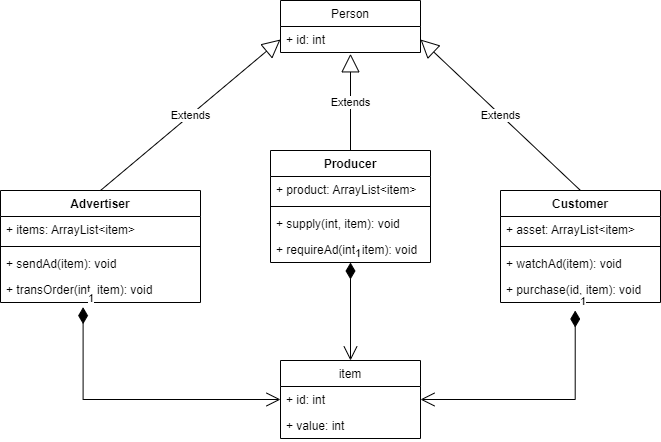
Advertiser/sendAd:
/*@ public normal_behavior
@ assignable items;
@ ensures items.length == \old(items.length) + 1;
@ ensures (\forall int i; 0 <= i && i < \old(items.length);
@ (\exists int j; 0 <= j && j < items.length; items[j].equals(\old(items[i]))));
@ ensures (\exists int i; 0 <= i && i < items.length; items[i].equals(item));
@*/
public void sendAd(Item item);
Producer/supply:
/*@ public normal_behavior
@ requires customers.contains(id);
@ assignable customers.get(id).asset;
@ ensures (\forall int i; 0 <= i && i < \old(customers.get(id).asset.length);
@ (\exists int j; 0 <= j && j < customers.get(id).asset.length;
customers.get(id).asset[j].equals(\old(customers.get(id).asset[i]))));
@ ensures (\exists int i; 0 <= i && i < customers.get(id).asset.legnth;
@ customers.get(id).asset[i].euqals(item)));
@also
@ public exceptional_behavior
@ assignable \nothing;
@ requires !customers.contains(id);
@ signals (PersonIdNotFoundException e) !customers.contains(id);
@*/
public void supply(int id, Item item);
Producer/requireAd:
/*@ public normal_behavior
@ requires products.contains(id);
@ assignable advertiser.get(id).items;
@ eusures (\forall int i; 0 <= i && i < \old(advertiser.get(id).items.length);
@ (\exists int j; 0 <= j && j < advertiser.get(id).items.length;
advertiser.get(id).items[i].equals(advertiser.get(id).items[j]))));
@ ensures (\exists int i; 0 <= i && i < advertiser.get(id).items.legnth;
@ advertiser.get(id).items[i].equals(item)));
@ also
@ public exceptional_behavior
@ assignable \nothin
@ requires !products.contains(id);
@ signals signals (PersonIdNotFoundException e) !products.contains(id);
@*/
public void requireAd(int id, Item item);
五、学习体会
在第三单元中,我们学习了契约式编程,掌握了JML的基本语法,尝试用JML去表达我们的需求,但这些并不是最主要的。JML也好,更加先进的其他契约式编程也好,都是我们所学习的“形”,而要学习的“神”则是契约式编程背后的新问题——如何组织一个庞大的团队去完成一个复杂的工程。
我认为契约式编程最大的优点,就是能够让程序员并不需要了解整个工程就可以参与其中,这极大地节约了时间成本,降低了对程序员素质的要求。契约式编程有些像管理学中的MPR:将最终产品拆分成一个个模块,模块再向下一层一层拆分,每一层的程序员只需要专注于项目的一小部分即可。这是从单打独斗到团队合作的转变,今后,我们将会逐渐习惯它、拥抱它。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号